微观孔洞演化的分子动力学研究进展

王佳坡 张梦浩 梁建伟 彭艳

摘要：先进金属材料如镍基单晶高温合金、特种钢材、钛合金、铝合金、3D打印多晶金属中普遍存在微孔洞。由于微孔洞演化和损伤机理性认识缺乏，微孔洞对材料性能影响尚未得到统一认识，关键在于实验手段难以获知应力、应变、能量等物理场。分子动力学模拟可以提供直观的原子运动信息，通常用来研究微孔洞演化对材料性能影响，为先进材料设计和性能调控提供理论依据。通过分子动力学计算得到的能量、应力、应变等，可以为更大尺度计算提供微孔洞演化物理本质。本文针对分子动力学模拟在微孔洞及其演化对材料性能影响的应用，从国内外研究现状出发，总结了当下热点和关键结论，分析了分子动力学应用存在的问题，对未来的发展趋势做出了展望。

关键词：微孔洞演化；分子动力学；先进材料；原子细节

中图分类号： V250.3文献标识码： ADOI：10.3969/j.issn.1007-791X.2024.02.001

0引言

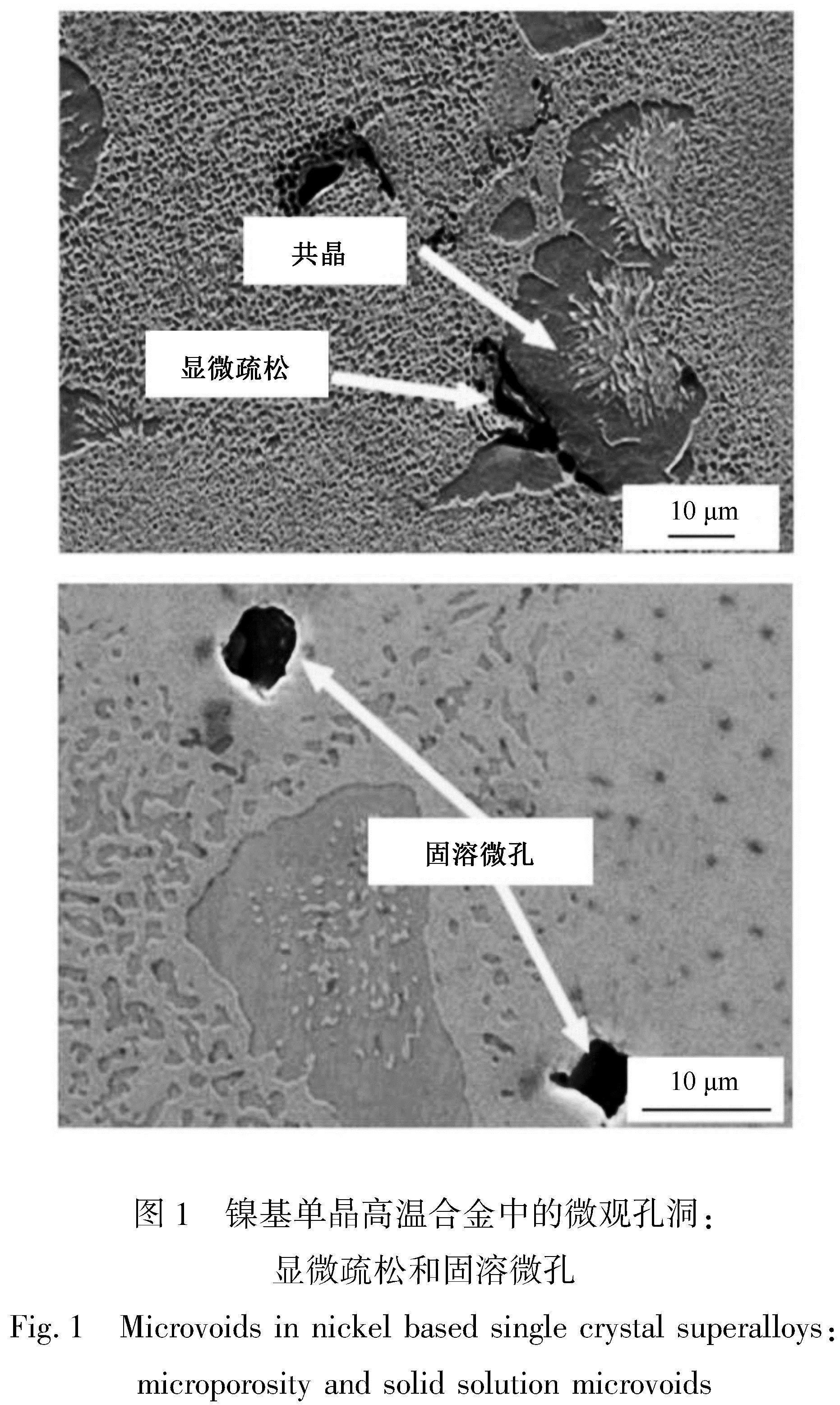
微孔洞的形核、生長和聚结被认为是延性材料破裂的主要机制。先进金属材料如航空发动机涡轮叶片用镍基单晶高温合金、高强高韧特种钢材、钛合金、铸造铝合金、3D打印多晶金属材料等中普遍观察到微孔洞的存在，并对上述材料的利用率、成品率、性能、生产效率等产生了明显的不良影响，微孔洞已成为先进金属材料制备和后续加工、服役过程中性能劣化难以忽略的瓶颈问题。铸造以及后续的热处理过程中，由于工艺等的影响，先进金属材料中不可避免地出现第三相夹杂、微孔洞、微裂纹等缺陷，对材料的性能产生了难以估计的影响，同时也为先进金属材料力学性能评估，相关金属结构部件的寿命预测提出了极大的挑战。以镍基单晶航空发动机涡轮叶片为例，在镍基单晶高温合金中，除了杂晶、雀斑、取向偏差和小角度晶界等常见缺陷外，微孔洞已成为影响合金力学性能的一个不可忽视的因素[1-2]。航空发动机涡轮叶片经历瞬时超温或超载，受到剧烈变化的热冲击载荷之后，涡轮叶片内部会产生初期的微损伤，扫描电子显微镜进一步观测研究表明，影响到叶片材料服役性能最初的微观破坏在于材料内部形成的大量的微孔洞（如图1所示[1]），以及微孔洞之间相互作用导致的较明显的初期微裂纹[3]。

目前，围绕微孔洞、微裂纹、第三相夹杂的研究已经引起了研究人员的极大关注。尤其是材料变形过程中的微孔洞变形行为，包括微孔洞生长、微孔洞聚结、微孔洞与其他缺陷之间的相互作用。现有研究结果表明：金属材料宏观变形断裂失效的原因在于裂纹扩展导致的有效承载面积降低。从微观角度进一步分析材料断裂失效表明微孔洞的生长聚结行为是主要原因，微孔洞的生长和聚结行为促使了微裂纹的形核和扩展，微裂纹的形核和扩展导致了宏观裂纹的形成，进而材料断裂失效。除此之外，微孔洞等的存在对材料的塑性变形机制也有明显的影响。上述问题均未得到系统的深入研究，现有研究大多数局限于微观试验手段和相关力学理论的建立，仍然停留在宏观到介观尺度，但是宏观唯象的研究手段对于材料力学性能的评估并不是很准确，并且不同材料需要大量的试验基础，误差诱因较多。所以从微观尺度出发，开展先进金属材料变形机理的研究对材料力学性能设计和新型功能材料的研发有重大意义，微观尺度变形机理的研究亟待开展。

微孔洞的形核、生长和聚结被认为是延性材料破裂的主要机制，其中微孔生长尤其重要。因此，有必要在考虑微观组织演变的情况下研究带孔材料的变形响应。以前关于微孔洞增长研究的大多数工作，包括实验和模拟方法，都被用来更好地描述韧性断裂过程。目前试验手段并不能实现微观尺度材料变形的直观观测，取而代之的是先进的数值模拟方法。一些数值方法，如晶体塑性有限元法[4-10]、位错动力学和分子动力学[11-22]，已被用来揭示微孔洞生长的机制。分子动力学（Molecular dynamics，MD）是基于原子间相互作用的微观模拟方法[23]，也是一种随计算机高速发展的强力模拟工具，在微观模拟方面具有独特的优势[24]，是研究材料微尺度断裂机理的有效工具。它可以直接观察原子的运动，获得原子尺度材料变形的细节。虽然MD方法在时空尺度上存在一定的局限性，通过MD模拟获得的材料力学性能数值不能代表材料真实的宏观力学性能，但大量的模拟结果表明，MD方法能够清楚地阐明材料的变形和破坏机制[25]，因此，MD被普遍应用于研究材料的微观变形机理，例如位错与微孔、夹杂、晶界等缺陷的相互作用。

目前为止，MD已经广泛地应用于特种材料和先进材料的研发、性能设计和调控过程中，在微孔洞演化机制和机理研究、微孔洞影响的变形损伤研究、微孔洞对性能的影响研究等领域取得了较大的进展。为了对MD在微孔洞相关研究领域的发展潜力有一个全面认识，本文从微孔洞形核、生长、塌缩、干涉、聚结以及与其他微结构相互作用方面对MD的应用进行了系统的综述，对微孔洞演化的原子细节和形式、微孔洞影响的力学性能变化规律进行了总结，并且对MD在微孔洞研究上的发展趋势和局限性进行了探讨。

1微孔洞形核

在大多数金属结构材料中，至少存在两种截然不同的相组织或其他夹杂粒子。从而研究人员结合大量试验观察总结了两种微孔洞形核机理，分别为应力形核和应变形核。应力形核来源于相组织界面应力超过阈值应力引起的相组织间界面分离或相组织自身破坏；而应变形核是基于位错累积模型，归因于等效塑形应变达到临界值后，引起的相组织-基体界面脱离。而进一步细观研究也提出了多种可能的形核假设：一是外力冲击下，刃型位错交互被当作微孔洞的起源；二是滑移带被晶粒边界或者各种缺陷拦截，堆积导致应力汇集，诱导该区域微孔洞成核；三是晶体内滑移带的焦点构成了残缺的位错墙，由于应力聚集促使微孔洞形成；四是第二相粒子或者基质内的沉积物，导致应力集中使该区域微孔洞成核[26-27]。考虑到不同金属材料微观组织等的差异，微孔洞形核机制也存在差异。但是有统一认识是微孔洞一般潜在的形核点是在材料内部的薄弱区域，微孔洞形核倾向于在交界点和界面处形核，如缺陷、晶界、相界面等微错易堆积、应力存在明显集中的点。上述这些区域破坏了材料微观结构连续性和完整性，容易引起局部的塑形流动，促使微孔洞的形核。随着SEM、TEM、XCT等先进测试技术发展，人们已经可以直观观察到上述微孔洞形核机制，然而，更深层次微纳尺度下微孔洞形核机理的准确揭示仍存在许多问题。比如对于静水张力加载下，位错塑性对微孔洞形核的影响等。近年来，MD的应用为微孔洞形核机理研究提供了更清晰的原子尺度视角。通过MD模拟，Zhao等人[28]研究了在静水张力载荷下理想晶格中的微孔洞形核，并预测塑性必须在孔洞均匀形核之前启动。同时他们也考虑了氢元素对微孔洞形核影响，建立了相关的数学描述模型，为储氢材料及设备研发提供了相关理论基础和思路。Yang等人[29]在各向同性和三轴应力条件下，通过MD研究了温度、应变率、初始压力、晶粒尺寸对微孔洞形核的影响，并指出微损伤过程分为图2所示四个阶段：原子无序、微孔洞形核、生长和聚结。而随着高端制造业、高精尖装备、核工业的发展，先进金属材料应用环境更加广泛，对于先进金属材料内部微孔洞缺陷的关注将会越来越多，在现有技术难以表征或者观察到的微孔洞形核机制原子尺度细节方面，MD模拟将展现出独有的异彩。

2微孔洞生长

MD模拟是揭示微孔洞生长机制的有效途径[30-34]。大量的MD模拟结果表明位错剪切环的发射是微孔生长的主要机制[8-10，35]。Tang等人[8]发现位错环的发射是微孔洞生长的主要原因，连续的位错成核和剪切环的增加促使微孔洞的生长。Dávila等人[10]在2004年提出了如图3所示棱柱环和剪切环的理论来描述多种材料内部孔洞生长塑性流动的微观机制。在这之前，棱柱环是早已被研究人员熟知的，比如Seppl等人[4]的研究表明棱柱环是孔洞生长的主要形式，孔洞的生长通过位错环的发射来实现。而剪切环的这个概念相对比较新颖。但是从微孔洞表面发射剪切位错环，类似于Ashby的几何必须位错，与试验观测比较符合。所以，针对棱柱环和剪切环这两种微孔洞生长微观机制则存在较大的争议。Bringa等人[12]开展了系列研究，并通过相关单轴拉伸模拟结果证实，剪切位错环是孔洞生长的首要机制，他们的模拟结果中并未观察到棱柱位错环。

国内外学者对影响微孔洞生长的其他因素，如尺寸效应[8，14-16]、初始微孔洞体积分数[8，17-20，30，34，36]和应变率[8，10，16]等，进行了大量MD模拟研究，得出在高速拉伸条件下的临界屈服应力对微孔半径、系统尺寸和温度的依赖性[34]：模型拉伸强度随着微孔半径与系统尺寸之比的减小而增加。主要原因在于微孔洞生长所需的应力的尺度依赖性被解释为随着孔洞尺寸的减小，最佳定向剪切面的可用性降低以及使剪切环成核所需的应力增加。基于位错环发射能量的分析方法，Tschopp等人总结得到了随微孔尺寸增加而减小的应力变化趋势[21]。Bhatia等使用MD研究了纳米微孔的生长行为，并揭示了其对微孔尺寸、应变速率、晶体加载取向、初始纳米微孔体积分数和模拟单元尺寸的相关性[5]。众所周知，单晶金属材料的力学性能与它们的晶体取向有很强的相关性。材料的加载取向不同，材料内部位错和剪切环会在不同的滑移系统上成核。微孔洞生长和破坏机制在不同的晶体取向上明显不同。因此，在该领域也开展了相关研究工作[15，18，22-25，37-38]。Potirniche等人[19]研究表明由初始晶格取向引起的塑性各向异性对微尺度区域中的微孔生长仅具有微小影响。变形过程中复杂的应力条件严重影响微孔的变形行为。Ha和Kim[22]的研究结果表明，应力三轴度是控制微孔生长和聚结的主要因素，应力三轴度和晶体取向决定的塑性变形模式对微孔的演化具有竞争效应。不同应力三轴度下，微孔洞的演化和形状改变差异很大：在高应力三轴度条件下，材料中微孔洞以體积改变为主，材料的破坏主要是由于材料的“孔洞化”效应造成；而在低应力三轴度条件下，微孔洞以形状改变为主。材料往往由于微孔洞的“内颈缩”而产生破坏。较低应力三轴度条件下，微孔变形主要由晶体取向决定。

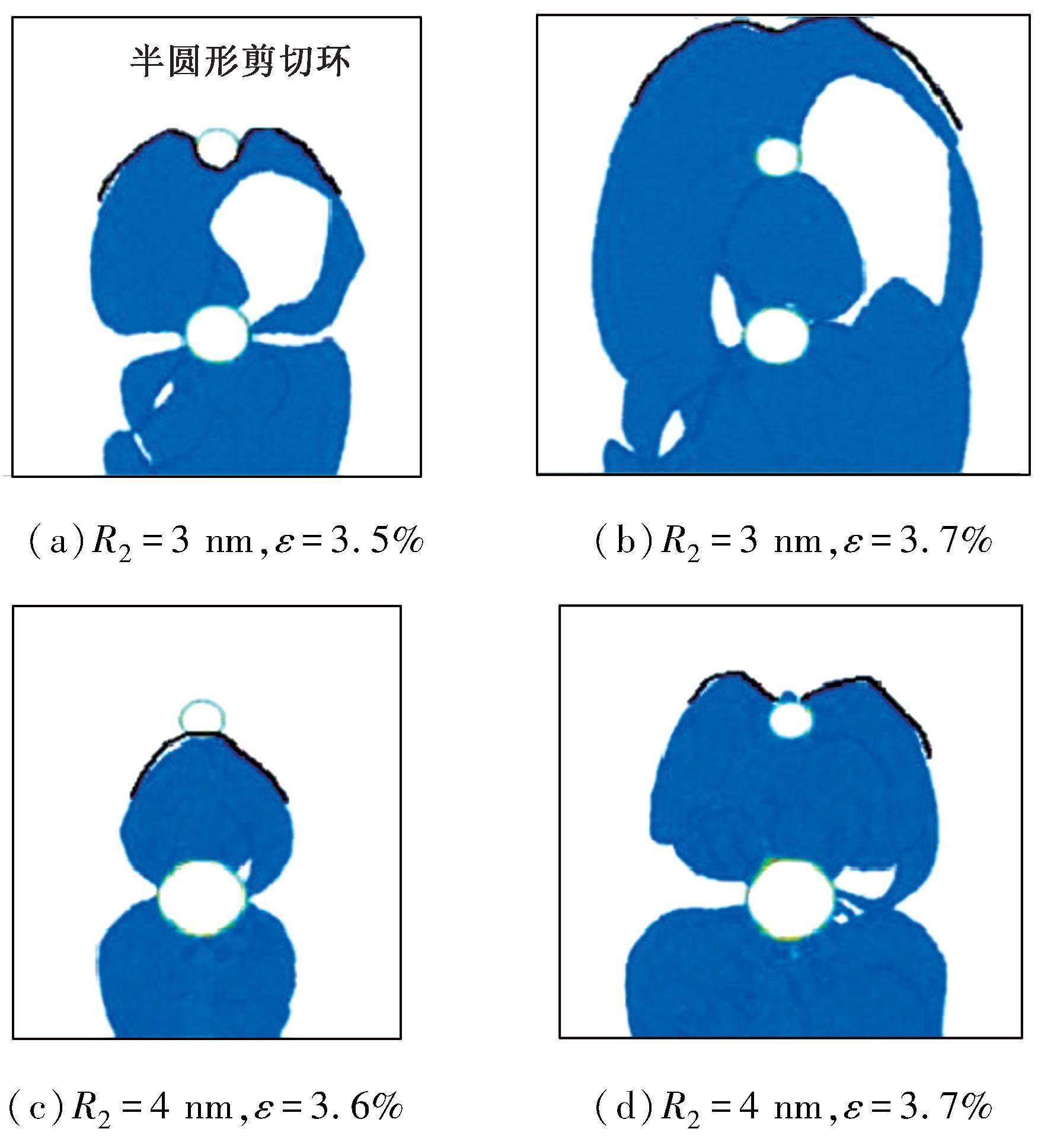
如图4所示，本课题组也开展了大量微孔洞生长的MD模拟，研究了典型晶体取向对镍基单晶基体相中微孔洞初始应力分布、位错成核发射、位错形态和应力-应变响应的影响[18，39]。考虑模型尺寸效应和微孔体积分数对微孔生长动力学进行了分析，基于计算和讨论，得到如下结论：不同尺寸和微孔体积分数的结果显示出对杨氏模量、初始屈服应力和初期屈服应变等力学性能的显著影响。进一步不同取向下微孔洞生长模拟的结果发现[100]、[110]和[111]取向的临界应力分别为6.97 GPa，6.77 GPa和7.31 GPa。基于图5展示的位错扩展和应力-应变响应结果对三种不同取向含微孔洞试样的弹塑性特性进行了解释[39]。在三个取向中，[111]取向试样的伸长率最大，这表明样品在相同的初始损伤中沿[111]取向具有良好的延展性。这与试验结果保持一致。与此同时，MD模拟得到了三种不同晶体取向原子系统中的位错演化，得到如下结论：1）微孔的自由表面是初始位错成核的位置，并且位错通过半圆形剪切环扩展。2）位错密度的演变与应力-应变曲线之间存在密切联系。在位错运动的初始阶段，位错密度缓慢增长，并且位错主要是Shockley局部位错。在应力-应变曲线的急剧下降阶段，位错增长率显著增加。3）在整个拉伸模拟过程中对位错长度演变的分析表明，[110]取向的位错长度最长，其次是[111]取向，[100]取向具有最短的位错长度。三种晶体取向的拉伸力学性能分析表明[110]取向屈服应力最小，更容易发生塑性变形。

综上，微孔洞生长机理的MD研究方面已取得了较大进展，然而尚未得到具有普适性的统一的描述，需要在考虑更多如微孔洞三维形貌、空间分布特征、应力状态、外部环境等影响因素的基础上建立微纳尺度下的微孔洞生长模型。

3微孔洞塌缩

科研人员普遍认为延性材料中微孔洞的生长和坍塌是基本事件，分别在整体拉伸和压缩载荷下导致材料失效[39]。微孔洞塌缩更多的被关注是在多孔材料在冲击和压缩下的响应问题，与微孔洞生长破坏相比，微孔洞塌缩导致的延性破坏得到关注度比较小。远场均匀应力作用下幂律材料中孤立微孔洞的变形理论研究发现最初球形微孔洞可能变成椭圆体并坍塌成裂缝或塌陷成针状。孔洞塌缩的数学描述一直是冲击压缩下材料本构方程发展的重要组成部分。但是目前关于冲击引起的孔洞坍塌的研究相对较少，只有基于位错的理论模型，其中微孔洞塌缩是通过形成快速滑动的棱柱位错环发射而发生的。相关模型已成功应用于冲击波通过多孔材料和粉末的传播，但并未解决导致孔洞塌缩的物理过程，其内在机制仍未得到有效认识。为了对微孔洞塌缩更全面的认识，自2000年后，逐渐有关于微孔洞塌缩MD研究的工作报道，Solanki等人[40]通过MD研究了单晶铜和镍中圆柱形孔洞在高应变速率下的部分塌缩和完全塌缩行为，并与有限元分析和试验结果在局部非弹性流动方面进行了对比，发现两者虽然存在较大的时空尺度差异，但是结果保持较大的一致性。Dávila等[10]开展了非平衡分子动力学计算表明，铜中冲击引起的微孔洞塌缩是通过剪切环的发射发生的，这与常规连续介质力学模型假设的棱柱环不同。Liao等[41]通过非平衡分子动力学系统地研究了在冲击压缩下具有分级微孔洞的 np-Ni 中的微孔洞塌缩，表明微孔洞的塌缩速率是冲击加载速度的线性函数，微孔洞塌缩初始表面位错位置取决于微孔洞在试样中的位置和微孔洞的尺寸梯度。

目前的研究表明，微孔洞生长的剪切环机制同时也作用于微孔洞塌缩，是微孔洞塌缩的主要机制之一。Guan等人[42]对单晶铝中微孔洞进行了1D和3D的MD压缩模拟以研究其塌缩行为及机制，模拟截图表明在1D和3D的压缩中均观察到如图6所示的位错剪切环从微孔洞表面发射，区别在于3D情况下，位错剪切环会汇合形成两个交叉的四面体，从而降低微孔洞的塌缩速率。除了以上面心立方金属之外，其他学者也对体心立方和密排六方金属中微孔洞塌缩行为进行了相关研究[43-44]，考虑了更多的因素，如温度、静水压力作用等等[45-47]，发现在较高温度下，空位扩散有助于位错移动并促进连续的微孔洞坍塌，而在较低温度下，质量传输和微孔洞塌缩通过位错的形成、滑移和相互作用发生，从而导致应变硬化。由于在较低温度下微孔洞周围的应变硬化，与较高温度相比，微孔洞坍塌在闭合初始阶段后延迟，使得微孔洞塌缩得到了进一步认识。但相对微孔洞生长研究仍然存在较大的差距，需要考虑更加复杂的因素，或者不同因素之间的协同和竞争作用进行细节讨论。除此之外，已有的微孔洞塌缩模拟研究相对冲击速率较大，对于低速加载下的影响机制尚未得到充分研究和认识。

4孔间干涉作用

微孔洞生长或者塌缩到一定程度会与近邻微孔洞进行聚结，但是在微孔洞生長变形后期和聚结前这一阶段，微孔洞之间的相互作用常常被忽视，而目前已经从试验现象中观察到了微孔洞间的相互扰动。这种孔间相互作用也可以称之为孔间干涉，微孔洞可以通过多种方式进行相互干涉作用，在纯碰撞的情况下，微孔洞仅仅是在它们各自增长到相互接触并连接在一起形成一个新孔洞的时候才相互作用，这时候相互作用就是微孔洞聚结。而实际情况表明微孔洞在物理空间接触之前就存在相互作用关系，这主要是由于在它们局部形成的弹性和塑性变形场，每个微孔洞局部都会产生一个通常与膨胀中心相关联形式的弹性应变场[48]，这个局部变形场促使它们的相互作用范围得到了扩展。比如剪切应力随着与微孔洞的距离的增加而减小，如r-3。而对于足够近的微孔洞，每个微孔洞的增长率都会被近端孔洞的应力场改变。弹性场的改变会影响其塑性变形的激活，以及微孔洞周围塑性区的后续变形扩展。微孔洞也可能通过它们的塑性场相互作用，在这种情况下，这些场可能会导致局部区域硬化速率增加或热软化和剪切局部化。对此，开展了不同的研究以探索微孔洞之间的相互作用临界距离。Brown 和 Embury[49]提出的基于简单几何考虑的向剪切变形过渡的论点表明，临界微孔洞间连接距离应等于一个微孔洞的直径；也就是说，当一对微孔洞的表面被一个微孔洞直径分开时，它们从独立的微孔洞生长过渡到相互作用。他们认为，正是在这一点上，占主导地位的微孔洞过程从围绕孤立生长的微孔洞的径向塑性流动转变为允许微孔洞对快速聚结的剪切变形。然而，最近的研究表明，对于大至六倍直径的微孔洞之间的距离，微孔洞增长率会提高[50]。Seppl[4]通过三维MD模拟开展了系列研究，包括通过微孔洞之间距离的减小速率、微孔洞的定向生长以及微孔洞的相关形状演变来量化微孔洞相互作用。验证了Brown 和 Embury的论点，检验了微孔洞的生长速率，表明微孔洞的相互作用没有反映在体积增长率中。本课题组同样开展了微孔洞之间相互作用的研究，大量宏微观研究表明孔间干涉始于滑移带，进一步通过开展图7所示不同构型的多个微孔洞的MD模拟，从弹性到塑性阶段研究了微孔洞的演化形式[51]，对比了不同构型下，微孔洞演化和相互作用对其基本力学性能的影响，并且分析了演化过程中孔洞的应力分布、应力三轴度变化趋势等。进一步分析了位错形核、位错密度和层错演化趋势，从而解析了微孔洞相互作用形式，总结出两种不同的变形机制：1）局部塑性变形;2）均匀的塑性变形。此外，局部塑性变形如下可以细分为局部颈缩和局部剪切，评估了微孔间干涉和孔间塑性变形机理。上述两种变形机制之间的差异主要是由堆垛层错与位错密度之间的竞争和协同作用引起的。局部塑性变形主要受堆垛层错控制，均匀的塑性变形主要是位错运动，只有少量的堆叠剪切运动。针对微孔洞之间的相互作用，下一步重点研究需要拓展到单轴拉伸的情况（以及微孔洞相对于拉伸方向的各种取向）、微孔洞相对于彼此的不同尺寸、其他晶体结构如体心立方和密排六方等。

5微孔洞聚结

就微孔洞之间的相互作用而言，微孔洞聚结对材料变形的影响最为明显[15，25]。目前，微孔洞聚结计算研究中考虑的主要因素是晶体取向、应力三轴度和微孔洞的空间构型[52]。已经尝试的微孔洞聚结行为的研究有：根据微孔洞的空间构型，或者是一对相邻微孔之间的几何微孔洞尺寸/间隔比[53]，或者包含规则阵列的非硬化材料的塑性加载极限变形[20，37，54]来模拟微孔洞聚结行为。Horstemeyer和Ramaswamy[55]以及Pardoen和Hutchinson[56]考虑了多种因素对微孔洞聚结进行详细的研究，如孔间间隔、形状和应变硬化系数。进一步研究中，Pardoen和Hutchinson根据两个聚结微孔洞之间的韧带取向将微孔洞聚结分为拉伸聚结或剪切聚结。任何微孔洞聚结模型都必须引入一些微观结构信息，例如微孔洞/接头长度和几何形状。从试验现象中已经观察到了微孔洞孔间干扰，并且总结了关于微孔洞聚结的不同机制[57]：第一种最常见的机制是通过孔间韧带的内部颈缩进行聚结。第二种微孔洞通过窄剪切板连接，这通常发生在剪切引起的微孔洞变形期间。Wen等人[58]研究了带孔平板中两种不同排布气膜孔周围的表面滑移变形特征，他们发现孔间干涉始于滑移带，Alinaghian报道了同样的现象[16]。第三种不常见的机制被称为柱状聚结或颈缩聚结，其中微孔洞沿其长度方向聚结。除了微孔洞聚结机制之外，微孔洞聚结的条件也受到广泛关注。Le等[59]描述了当微孔洞的最长轴是平均平面相邻间距的数量级时发生微孔洞聚结。Koplik和Needleman通过进行单胞分析[60]确定微孔洞聚结的开始，其中当单元格的宏观变形转变为单轴拉伸状态时，发生微孔洞聚结。所有这些都指出了多孔材料塑性变形中微孔洞生长和聚结的重要性。

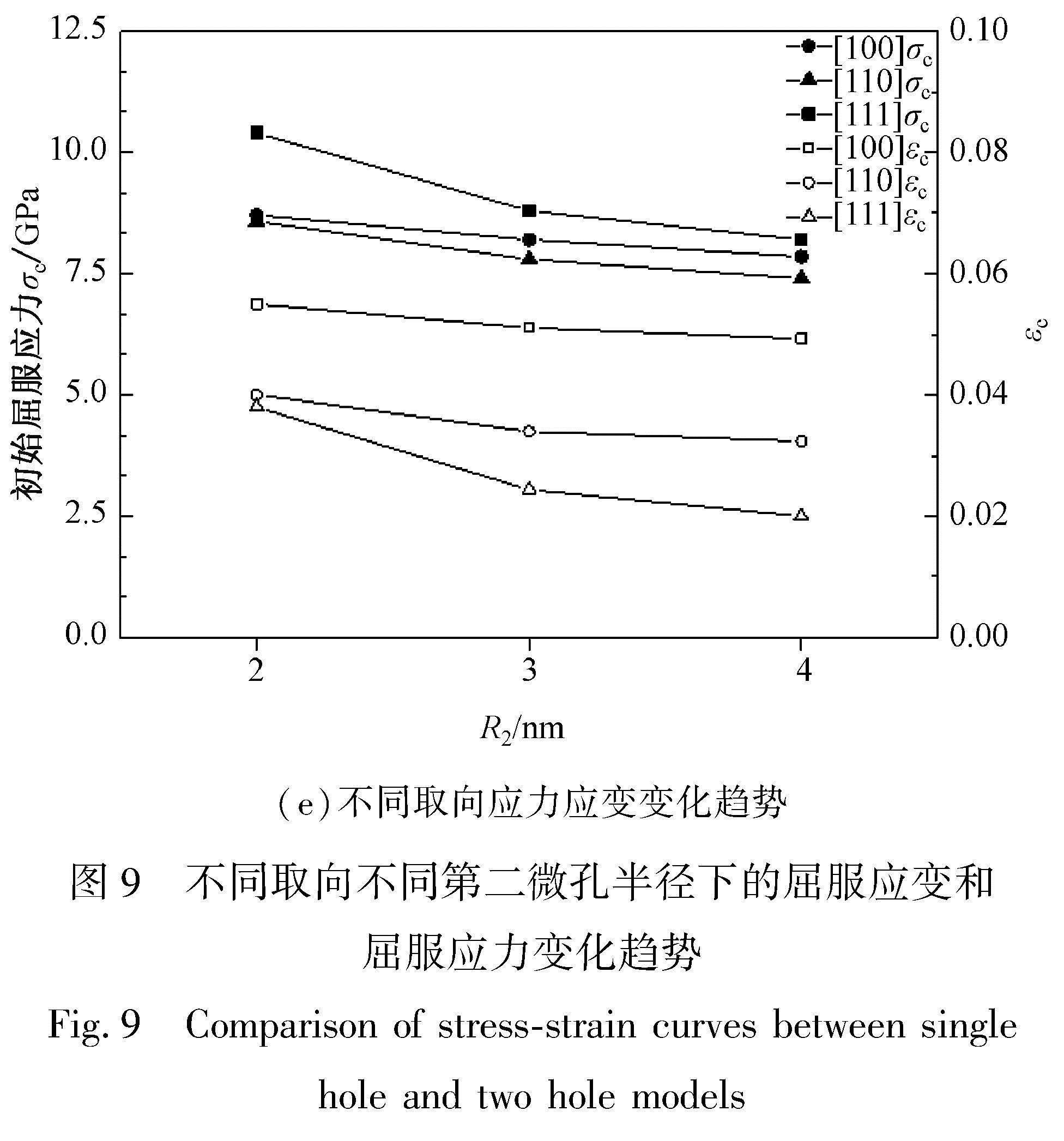
通过再现原子尺度的结构演化，包括位错运动和原子扩散[61-62]，微孔洞聚结的MD模拟可以提供在较大规模的模拟研究中无法获得的重要优势。Seppl在MD研究中发现一对孤立微孔洞聚结过程与具有周期性边界的单个微孔洞的聚结过程明显不同，因此后者无法提供典型低对称配置中聚结的可靠描述[4]。Zhao等人考虑两个孔洞初始半径和空间距离这两个影响因素，通过MD模拟研究了单晶铜中两个孔洞的生长和聚结[63]，发现应力三轴度的峰值随着初始微孔洞韧带距离的增加而增大，直至达到微孔洞聚结的临界点，然后减小。这表明应力三轴度可能是表征微孔洞聚结是否产生的重要指标。除了单纯的研究微孔洞自身演化机理，MD还通常被用来研究微孔洞聚合对材料机械和力学性能的影响，为先进材料的设计和性能调控提供理论依据。如Tran等[64]通过MD 模拟研究了在拉伸过程中具有一孔和二孔缺陷的 Cu-Ta 金属玻璃纳米薄膜的变形机制和机械性能，他们发现二孔试件的抗拉强度高于一孔试件，但破坏速度较快。这种现象在早年间Mi等人的研究中也有报道[65]，相关表述为在空隙率恒定的情况下，多孔样品通常会通过更强烈的位错相互作用产生比单孔洞样品更高的屈服应力和更高的承载能力。这一观察表明，通过在纳米尺度上将一个大的孔洞重新分配成多个小的孔洞，可以提高样品的应力阻力，然而，在空隙率恒定的情况下，空隙率的演變似乎与孔洞数无关，没有记录到由于相邻孔洞的聚结而导致的孔洞膨胀的明显加速。Gao等人使用MD模拟研究了微孔洞对 FeNiCrCoCu 高熵合金机械性能的影响，考虑到不同的微孔洞尺寸、施加的应变率和温度，通过使用具有一个或两个微孔洞的模型来检查微孔洞的演变行为[66]。本课题组也开展了微孔洞聚结的MD模拟研究工作，主要是从晶体取向（图8）和微孔洞初始半径（图9）这两个方面讨论了镍基单晶合金基体相中微孔洞的聚演化行为，得到了相关应力-应变曲线等力学性能参数和微错演化等微观变形机制[67]，并且发现相对单孔，两孔材料更容易发生塑形变形。

综上所述，微孔洞聚结行为作为延性材料断裂失效过程重要一环，已经逐渐受到了更加明显的关注，尤其是在新兴材料和高端制造行业，后期在微纳加工以及纳米晶等材料服役性能方面更需要重点考虑，而MD作为大规模的原子尺度分析计算手段，将为上述材料的性能设计、性能调控策略、性能和服役寿命评估提供底层的理论依据。

6微孔洞与其它微结构的相互作用

MD研究微孔洞生长和合并行为绝大部分都集中在单相材料上，但是自然界中大多数金属材料的力学性能是各向异性的，例如镍基单晶高温合金，材料中存在许多性能迥异的微观结构，如不同晶体取向和相界面，这也会极大地影响到微孔洞的生长和聚合行为[52]。所以对于多相材料或多晶材料来说，微孔洞的外部环境对材料的力学性能也有影响，特别是如果微孔洞出现在相界面上，材料的承载能力将大大降低。并且由于不同相组织的结构和晶胞物理性能差异，微孔洞的变形生长也不尽相同。所以非常有必要开展缺陷位置（即不同微观组织结构的基体材料）对材料内部微孔洞的变形生长行为以及材料力学性能影响的研究。近年来针对微孔洞等缺陷和不同微观组织间相互作用开展了越来越多的工作[68-71]。但由于微孔洞和微观组织结构的尺寸较小，除了少量高成本的高分辨率TEM下的原位试验之外，现有的试验测试方法不能支持对材料变形机制的直观观察。MD模拟为实时观察原子运动并获得微孔洞和不同微观组织结构间的相互作用机制提供了便捷途径，已经广泛应用于核反应堆材料[72-74]、先进高温合金[75-76]等内部的微孔洞与位错[77-78]、沉淀相、微裂纹[69]等的相互作用导致的力学性能和耐辐照性能的变化，如图10所示[79]。

在辐照缺陷导致反应器材料的机械性能下降的工业背景下，为了厘清反应器材料中位错和缺陷之间的关系，Yabuuchi等人[73]使用MD研究刃位错与不同刻面微孔洞几何组合之间的相互作用，以阐明切削机制和微孔洞对纯铁辐照硬化的影响。Cui等人[75]研究了冲击波与预先存在的纳米空隙的相互作用以及剪应力在铁相变过程中的作用。纳米空隙是铁相变最喜欢的成核位点，它加速了相变区的生长，孔洞降低了阈值压力并加快了成核速度，从而使新相更容易生成和生长，同时也阐明孔洞的尺寸会影响相转变的过程。作者团队考虑航空发动机涡轮叶片材料镍基单晶高温合金的复杂微观结构，建立了图11所示Ni，Ni3Al和Ni/Ni3Al界面模型，分析了微孔洞在这三种不同微观组织结构中的扩展动力学，此外，在不同的模型下评估了微孔体积分数对材料的拉伸性能和断裂机理的影响[76]。Yang等人用MD方法研究了镍基单晶高温合金中γ/γ′相的纳米压痕变形行为[68]，结果表明带孔模型中位错的成核要滞后于理想模型，原因在于微孔洞坍塌消耗了累积的应变能。Cui等人[75]针对位错和强化相间相互作用对镍基单晶高温合金的强化机理，考虑了微孔洞对该变形机理的影响作用，他们研究表明微孔洞等缺陷的存在会降低位错进入强化相的难度，从而降低强化效应，导致镍基单晶高温合金力学性能降低。了解微孔洞和晶界之间的相互作用对于通过晶界工程设计抗辐射材料和实现高质量的冶金扩散连接非常重要。迁移的晶界可以被固定到微孔洞，或自由穿过微孔洞，或在它们相互作用后完全溶解微孔洞，MD模拟表明较高温度可以显著提高大角度晶界溶解微孔洞的能力[74]。Zhang等人[80]采用MD模拟研究了微孔洞生长对纳米级三晶镍薄膜中晶界三重结取向的依赖关系，结果表明Shockley局部位错在晶界三重结的微孔洞生长中起主导作用。裂纹与微孔洞之间的相互作用研究发现裂纹扩展行为极易受微孔洞分布的影响[66]，在裂纹尖端存在单个的微孔洞可能通过裂纹-微孔洞相互作用影响裂纹传播方向及速度。

上述内容表明，微孔洞与微结构相互作用或者考虑微孔洞影响的微观结构演化相关MD研究在核工业，尤其是核反应材料的力学性能和辐照损伤变形设计和研发方面，先进航空发动机叶片材料高温合金等方面取得了明显的成果和进展，而随着越来越多的先进材料的研发和应用、多孔特种材料等的发展，微孔洞的影响将会得到更多研究人员的关注，微孔洞与微观结构演化的相互作用的MD模拟会逐步扩展到更严苛的环境（热-力-电耦合）、更高精度（微纳加工和微纳制造）、更深层次（统一理论模型）、更大规模（近实验的时空一致计算）。

7討论与展望

1） MD由于其独特的优势，在研究微孔洞演化行为方面得到了重点关注。MD模拟技术既能得到原子的运动轨迹，还能像做实验一样观察特别是许多与原子有关的微观细节，在实验中无法获得，而在计算机模拟中可以方便得到[81-83]。这种优点使得MD方法广泛运用于断裂分析等材料科学与工程中。但是目前为止，微孔洞演化方面的理论研究仍然集中在连续介质力学方面。虽然有部分研究对比了MD与连续介质力学在微孔洞演化方面的计算或预测结果，但是MD与更大尺度的连续介质力学之间的时间和空间尺度的差异仍是微孔洞演化行为等微观结构与宏观力学表现之间的关系建立的挑战。MD研究微观结构演化的最终目的是构建起微观结构演化和力学表现的数学映射关系，所以进一步需要在MD模拟的基础上，结合位错动力学、相场模型等更大尺度的模型，构建或提出具有一般意义的普适的多尺度方法或微孔洞演化模型，既能够反映微孔洞演化行为，又能够与宏观性能进行对比和预测。

2） MD特别适合用来研究在非常高的应变率下（107～1010/s）的微孔洞增长（对应于冲击等试验）。

3） 随着先进观测技术的发展，微观孔洞演化的动态过程已经可以通过同步辐射断层扫描XCT等进行直观观测，但是试验观测到最小的微孔洞尺寸仍是100 nm大小，相对目前MD模拟的0.1～50 nm的尺寸大至少一个量级，所以需要考虑更接近于试验、贴合实际的更大规模的MD模拟计算。当然这与计算资源和成本息息相关。

4） MD模拟的最大的局限性不是计算资源带来的计算规模的大小，而是模拟体系中原子间相互作用力的准确描述。目前MD模拟微孔洞的生长、聚结等行为都是在单一原子、单一相下进行，计算体系仅包含少量元素，其最主要的原因是势函数的拟合挑战。目前包含元素最多的势函数是高熵合金的势函数，包含5个元素的相互作用，其余大多为三元合金、二元合金。但实际情况下，理想的纯金属并不存在，大多数金属材料包含不下于10种元素，且这些元素与金属的宏观性能和微观结构演化密切相关。比如，镍基单晶合金中大量的固溶元素，如Re、Cr、Co等，这些元素不易扩散，容易聚集形成第三相夹杂，而这种夹杂也是微孔洞形核和生长更易发生的区域。所以，需要考虑更多元素、更复杂的合金体系来研究微孔洞演化行为。

参考文献

[1] 于军伟，康茂东，刘雅辉，等.镍基单晶高温合金微观孔洞缺陷研究进展 [J]. 铸造技术，2018，39（11）： 2615-2619.

YU J W，KANG M D，LIU Y H，et al. Research progress on micro pore defects in nickel based single crystal high-temperature alloys [J].Foundry Technology，2018，39 （11）： 2615-2619.

[2] 赵新宝，刘林，杨初斌，等. 镍基单晶高温合金凝固缺陷研究进展 [J]. 材料工程，2012（1）： 93-98.

ZHAO X B，LIU L，YANG C B，et al. Research progress on solidification defects in nickel based single crystal superalloys [J].Materials Engineering，2012（1）： 93-98.

[3] 童锦艳，冯微，付超，等. GH4033合金短时超温后的显微组织损伤及力学性能 [J]. 金属学报，2015，51（10）： 1242-1252.

TONG J Y，FENG W，FU C，et al. Microstructural damage and mechanical properties of GH4033 alloy after short-term overtemperature [J].Acta Metallurgica Sinica，2015，51（10）： 1242-1452.

[4] SEPPL E T，BELAK J，RUDD R E. Three-dimensional molecular dynamics simulations of void coalescence during dynamic fracture of ductile metals [J]. Physical Review B，2005，71（6）： 064112.

[5] BHATIA M A，SOLANKI K N，MOITRA A，et al. Investigating damage evolution at the nanoscale： molecular dynamics simulations of nanovoid growth in single-crystal aluminum [J]. Metallurgical and Materials Transactions A，2012，44（2）： 617-626.

[6] SEPPL E T，BELAK J，RUDD R E. Effect of stress triaxiality on void growth in dynamic fracture of metals： a molecular dynamics study [J]. Physical Revew B，2004，69（13）： 13401.

[7] SEPPL E T，BELAK J，RUDD R E. Onset of void coalescence during dynamic fracture of ductile metals [J]. Physical Review Letters，2004，93（24）： 245503.

[8] TANG F L，CAI H M，BAO H W，et al. Molecular dynamics simulations of void growth in γ-TiAl single crystal [J]. Computational Materials Science，2014，84： 232-237.

[9] MEYERS M A，TRAIVIRATANA S，LUBARDA V A ，et al. The role of dislocations in the growth of nanosized voids in ductile failure of metals [J]. JOM，2009，61（2）： 35-41.

[10] DAVILA L，ERHART P，BRINGA E，MEYERS M，et al. Atomistic modeling of shock-induced void collapse in copper [J]. Applied Physics Letters，2005，86（16）： 161902.

[11] HORSTEMEYER M F，BASKES M I，PLIMPTON S J. Length scale and time scale effects on the plastic flow of fcc metals [J]. Acta Materialia，2001，49（20）： 4363-4374.

[12] BRINGA E M，TRAIVIRATANA S，MEYERS M A. Void initiation in fcc metals： effect of loading orientation and nanocrystalline effects [J]. Acta Materialia，2010，58（13）： 4458-4477.

[13] POTIRNICHE G P，HORSTEMEYER M F，WAGNER G J，et al. A molecular dynamics study of void growth and coalescence in single crystal nickel [J]. International Journal of Plasticity，2006，22（2）： 257-278.

[14] CHANG H J，SEGURADO J，LLORCA J. Three-dimensional dislocation dynamics analysis of size effects on void growth [J]. Scripta Materialia，2015，95： 11-14.

[15] SEGURADO J，LLORCA J. Discrete dislocation dynamics analysis of the effect of lattice orientation on void growth in single crystals [J]. International Journal of Plasticity，2010，26（6）： 806-819.

[16] ALINAGHIAN Y，ASADI M，WECK A. Effect of pre-strain and work hardening rate on void growth and coalescence in AA5052 [J]. International Journal of Plasticity，2014，53： 193-205.

[17] LIU W H，ZHANG X M，TANG J G，et al. Simulation of void growth and coalescence behavior with 3D crystal plasticity theory [J]. Computational Materials Science，2007，40（1）： 130-139.

[18] TANG Y，BRINGA E M，MEYERS M A. Ductile tensile failure in metals through initiation and growth of nanosized voids [J]. Acta Materialia，2012，60（12）： 4856-4865.

[19] POTIRNICHE G P，HEARNDON J L，HORSTEMEYER M F ，et al. Lattice orientation effects on void growth and coalescence in fcc single crystals [J]. International Journal of Plasticity，2006，22（5）： 921-942.

[20] TSCHOPP M A，MCDOWELL D L. Influence of single crystal orientation on homogeneous dislocation nucleation under uniaxial loading [J]. Journal of the Mechanics and Physical of Solids，2008，56（5）： 1806-1830.

[21] TSCHOPP M A，SPEAROT D E，MCDOWELL D L. Atomistic simulations of homogeneous dislocation nucleation in single crystal copper [J]. Modelling and Simulation in Materials Science and Engineering，2007，15（7）： 693-699.

[22] HA S，KIM K. Void growth and coalescence in f.c.c. single crystals [J]. International Journal of Mechanical Sciences，2010，52（7）： 863-873.

[23] 田楠，仝永剛，赵超杰，等.分子动力学方法在高熵合金研究中的应用现状与展望[J].中国有色金属学报，2023，33（1）：100-111.

TIAN N，TONG Y G，ZHAO C J，et al. Application status and prospects of molecular dynamics methods in the study of high entropy alloys [J]. Chinese Journal of Nonferrous Metals，2023，33 （1）： 100-111.

[24] 王嘉楠，伍鲍，何安民，等.强冲击下金属材料动态损伤与破坏的分子动力学模拟研究进展[J].高压物理学报，2021，35（4）：4-17.

WANG J N，WU B，HE A M，et al. Progress in molecular dynamics simulation of dynamic damage and failure of metal materials under strong impact [J]. Journal of High Pressure Physics，2021，35 （4）： 4-17.

[25] ZHU L，RUAN H H，LI X Y，et al. Modeling grain size dependent optimal twin spacing for achieving ultimate high strength and related high ductility in nanotwinned metals[J]. Acta Materialia，2011，59（14）： 5544-5557.

[26] NOELL P J，SILLS R B，BENZERGA A A，et al. Void nucleation during ductile rupture of metals： a review [J]. Progress in Materials Science，2023，135： 101085.

[27] LI C，YANG K，GAO Y H，WANG L. Dislocation-dominated void nucleation in shock-spalled single crystal copper： Mechanism and anisotropy [J]. International Journal of Plasticity，2022，155： 103331.

[28] ZHAO K，HE J，RINGDALEN I G，et al. Effect of amorphization-mediated plasticity on the hydrogen-void interaction in ideal lattices under hydrostatic tension [J]. Journal of Applied Physics，2018，123（24）： 245101.

[29] YANG X，ZENG X，WANG J，et al. Atomic-scale modeling of the void nucleation，growth，and coalescence in Al at high strain rates [J]. Mechanics of Materials，2019，135： 98-113.

[30] TRAIVIRATANA S，BRINGA E M，BENSON D J，et al. Void growth in metals： atomistic calculations [J]. Acta Materialia，2008，56（15）： 3874-86.

[31] LUBARDA V A，SCHNEIDER M S，KALANTAR D H，et al. Void growth by dislocation emission [J]. Acta Materialia，2004，52（6）： 1397-1408.

[32] MARIAN J，KNAP J，ORTIZ M. Nanovoid deformation in aluminum under simple shear [J]. Acta Materialia，2005，53（10）： 2893-2900.

[33] WANG L，ZHOU J，HUI D，et al. Micromechanics model for nanovoid growth and coalescence by dislocation emission： loading and lattice orientation effects [J].International Journal of Mechanical Sciences，2014，79： 168-175.

[34] KRASNIKOV V S，MAYER A E. Plasticity driven growth of nanovoids and strength of aluminum at high rate tension： molecular dynamics simulations and continuum modeling [J]. International Journal of Plasticity，2015，74： 75-91.

[35] RUDD R E，BELAK J F. Void nucleation and associated plasticity in dynamic fracture of polycrystalline copper： an atomistic simulation [J]. Computational Materials Science，2002，24（1/2）： 148-153.

[36] KRASNIKOV V S， MAYER A E. Plasticity driven growth of nanovoids and strength of aluminum at high rate tension： molecular dynamics simulations and continuum modeling[J] . International Journal of Plasticity， 2015， 74： 75-91.

[37] SRIVASTAVA A，NEEDLEMAN A. Effect of crystal orientation on porosity evolution in a creeping single crystal [J]. Mechanics of Materials，2015，90： 10-29.

[38] FARRISSEY L，LUDWIG M，MCHUGH P E，et al. An atomistic study of void growth in single crystalline copper [J]. Computational Materials Science，2000，18（1）： 102-117.

[39] WANG J P， YUE Z F， WEN Z X， et al. Orientation effects on the tensile properties of single crystal nickel with nanovoid： atomistic simulation[J]. Computational Materials Science， 2017， 132： 116-124.

[40] SOLANKI K，HORSTEMEYER M F，BASKES M I，et al. Multiscale study of dynamic void collapse in single crystals [J]. Mechanics of Materials，2005，37（2）： 317-330.

[41] LIAO Y，XIANG M，LI G，et al. Molecular dynamics studies on energy dissipation and void collapse in graded nanoporous nickel under shock compression [J]. Mechanics of Materials，2018，126： 13-25.

[42] GUAN Y L，SHAO J L，SONG W. Molecular dynamics study on nanoscale void collapse in single crystal aluminum under 1D and 3D compressions [J]. Computational Materials Science，2019，161： 385-393.

[43] XU Q，LI W，ZHOU J，et al. Molecular dynamics study on void collapse in single crystal hcp-Ti under hydrostatic compression [J]. Computational Materials Science，2020，171： 109280.

[44] GALITSKIY S，MISHRA A，DONGARE A M. Modeling shock-induced void collapse in single-crystal Ta systems at the mesoscales [J]. International Journal of Plasticity，2023，164： 103596.

[45] GUAN Y L，DAI L S，SHAO J L，et al. Molecular dynamics study on the nanovoid collapse and local deformation in shocked Cu50Zr50 metallic glasses [J]. Journal of Non-Crystalline Solids，2021，559： 120703.

[46] PRASAD M R G，NEOGI A，VAJRAGUPTA N，et al. Influence of temperature on void collapse in single crystal nickel under hydrostatic compression [J]. Materials，2021，14（9）： 2369.

[47] CHEN Z，ZHANG X，LI W，et al. Shock compression of nanoporous silicon carbide at high strain rate [J]. International Journal of Mechanical Sciences，2022，224： 107320.

[48] ESHELY J D，PEIERLS R E. The elastic field outside an ellipsoidal inclusion [J]. Proceedings of the Royal Society of London：Series A Mathematical and Physical Sciences，1959，252（1271）： 561-569.

[49] BROWN L，EMBURY J. Microstructure and design of alloys[C]//Proceedings of the 3rd International Conference on the Strength of Metals and Alloys， Cambridge， England，1973.

[50] HORSTEMEYER M，MATALANIS M，SIEBER A，et al. Micromechanical finite element calculations of temperature and void configuration effects on void growth and coalescence [J]. International Journal of Plasticity，2000，16（7/8）： 979-1015.

[51] WANG J，LIANG J，WEN Z，et al. Void configuration-induced change in microstructure and deformation mechanisms of nano-porous materials [J]. Journal of Applied Physics，2019，126（8）： 085106.

[52] BANDSTRA J P，KOSS D A. A simulation of growth and coalescence of voids during ductile fracture [J]. Materials Science and Engineering： A，2004，387： 399-403.

[53] LEBENSOHN R A，ESCOBEDO J P，CERRETA E K，et al. Modeling void growth in polycrystalline materials [J].Acta Materialia，2013，61（18）： 6918-6932.

[54] NEMCKO M J，QIAO H，WU P，et al. Effects of void fraction on void growth and linkage in commercially pure magnesium [J]. Acta Materialia，2016，113： 68-80.

[55] HORSTEMEYER M F，RAMASWAMY S. On factors affecting localization and void growth in ductile metals：a parametric study [J]. International Journal of Damage Mechanics，2000，9（1）： 5-28.

[56] PARDOEN T，HUTCHINSON J W. An extended model for void growth and coalescence [J].Journal of the Mechanics and Physics of Solids，2000，48（12）： 2467-2512.

[57] TREJO NAVAS V M，BERNACKI M，BOUCHARD P O. Void growth and coalescence in a three-dimensional non-periodic void cluster [J]. International Journal of Solids and Structures，2018，139-140： 65-78.

[58] WEN Z X，LI Z W，ZHANG Y M，et al. Surface slip deformation characteristics for perforated Ni-based single crystal thin plates with square and triangular penetration patterns [J]. Materials Science and Engineering： A，2018，723： 56-69.

[59] LE ROY G，EMBURY J D，EDWARDS G，et al. A model of ductile fracture based on the nucleation and growth of voids [J]. Acta Metallurgica，1981，29（8）： 1509-1522.

[60] KOPLIK J，NEEDLEMAN A. Void growth and coalescence in porous plastic solids [J]. International Journal of Solids and Structures，1988，24（8）： 835-853.

[61] SONG H Y，LI S，DENG Q. Coupling effects of thickness and aspect ratio on deformation behavior of Cu50Zr50 metallic glass [J]. Computational Materials Science，2017，139： 106-114.

[62] SONG H Y，LI S，ZHANG Y G ，et al. Atomic simulations of plastic deformation behavior of Cu50Zr50 metallic glass [J]. Journal of Non-Crystalline Solids，2017，471： 312-321.

[63] ZHAO L，LIU Y. Investigation on void growth and coalescence in single crystal copper under high-strain-rate tensile loading by atomistic simulation [J]. Mechanics of Materials，2020，151： 103615.

[64] TRAN A S，FANG T H. Void growth and coalescence in Cu-Ta metallic glasses using molecular dynamics [J]. Computational Materials Science，2019，168： 144-153.

[65] MI C，BUTTRY D A，SHARMA P ，et al. Atomistic insights into dislocation-based mechanisms of void growth and coalescence [J]. Journal of the Mechanics and Physics of Solids，2011，59（9）： 1858-1871.

[66] GAO T，SONG H，WANG B，et al. Molecular dynamics simulations of tensile response for FeNiCrCoCu high-entropy alloy with voids [J]. International Journal of Mechanical Sciences，2023，237： 107800.

[67] WEN Z X，WANG J P，WU Y W，et al. Atomistic simulation analysis of the effects of void interaction on void growth and coalescence in a metallic system [J]. Current Applied Physics，2018，18（6）： 744-751.

[68] YANG B，ZHENG B，HU X，et al. Atomistic simulation of nanoindentation on incipient plasticity and dislocation evolution in γ/γ′ phase with interface and void [J]. Computational Materials Science，2016，114： 172-177.

[69] WANG L，LIU Q，SHEN S. Effects of void-crack interaction and void distribution on crack propagation in single crystal silicon [J]. Engineering Fracture Mechanics，2015，146： 56-66.

[70] LIANG S，HUANG M，LI Z. Discrete dislocation modeling on interaction between type-I blunt crack and cylindrical void in single crystals [J]. International Journal of Solids and Structures，2015，56-57： 209-219.

[71] LIU T，GROH S. Atomistic modeling of the crack-void interaction in α-Fe [J]. Materials Science and Engineering： A，2014，609： 255-265.

[72] DOU Y K，CAO H，HE X F，et al. Interaction mechanism of an edge dislocation with a void in Fe-Ni-Cr concentrated solid-solution alloy [J]. Journal of Alloys and Compounds，2021，857： 157556.

[73] YABUUCHI K，SUZUDO T. Interaction between an edge dislocation and faceted voids in body-centered cubic Fe [J]. Journal of Nuclear Materials，2023，574： 154161.

[74] ZHANG L，SHIBUTA Y，LU C，et al. Interaction between nano-voids and migrating grain boundary by molecular dynamics simulation [J]. Acta Materialia，2019，173： 206-224.

[75] CUI C，GONG X，CHEN L，et al. Atomic-scale investigations on dislocation-precipitate interactions influenced by voids in Ni-based superalloys [J]. International Journal of Mechanical Sciences，2022，216： 106945.

[76] WANG J P，LIANG J W，WEN Z X，et al. Atomic simulation of void location effect on the void growth in nickel-based single crystal [J]. Computational Materials Science，2019，160： 245-255.

[77] ZHU B，HUANG M，LI Z. Atomic level simulations of interaction between edge dislocations and irradiation induced ellipsoidal voids in alpha-iron [J]. Nuclear Instruments and Methods in Physics Research：Section B Beam Interactions with Materials and Atoms，2017，397： 51-61.

[78] BAHRAMYAN M，MOUSAVIAN R T，BRABAZON D. Molecular dynamic simulation of edge dislocation-void interaction in pure Al and Al-Mg alloy [J]. Materials Science and Engineering： A，2016，674： 82-90.

[79] XIONG L M， XU S Z， MCDOWELL D L， et al. Concurrent atomistic-continuum simulations of dislocation-void interactions in fcc crystals[J]. International Journal of Plasticity， 2015， 65： 33-42.

[80] ZHANG Y，JIANG S，ZHU X，et al. Orientation dependence of void growth at triple junction of grain boundaries in nanoscale tricrystal nickel film subjected to uniaxial tensile loading [J]. Journal of Physics and Chemistry of Solids，2016，98：220-232.

[81] 梁華，李茂生.孔洞和空位对单晶铝力学性能影响的分子动力学研究[J].计算物理，2019，36（2）：211-218.

LIANG H，LI M S. Molecular dynamics study on the effects of pores and vacancies on the mechanical properties of single crystal aluminum [J]. Computational Physics，2019，36 （2）： 211-218.

[82] 单德彬，袁林，郭斌.分子动力学模拟在裂纹萌生和扩展中的研究进展[J].兵器科学与工程，2003（3）：63-67.

SHAN D B，YUAN L，GUO B. Research progress of molecular dynamics simulation in crack initiation and propagation [J]. Weapon Science and Engineering，2003 （3）： 63-67.

[83] 王煜烨，汤爱涛，潘荣剑，等.分子动力学在镁及镁合金微观塑性变形中的应用进展[J].材料导报，2019，33（19）：3290-3297.

Advances in molecular dynamics research of microvoid evolution

Abstract： Microvoids are commonly observed in advanced metal materials such as nickel-based single crystal superalloys，special steels，titanium alloys，cast aluminum alloys，and 3D printed polycrystalline metal materials. Due to the lack of mechanistic understanding of microvoids evolution and damage，the influence of microvoids on material properties has not yet been unified. The important reason is that it is difficult to obtain various physical fields such as stress，strain，and energy by experimental means. Molecular dynamics simulation （MD） can provide intuitive dynamic evolution information from the details of atomic motion，is often used to study the influence of microvoids aggregation on the mechanical properties of materials，providing a theoretical basis for the design and performance regulation of advanced materials. Through the quantitative processing of physical quantities such as energy，atomic stress，and strain obtained by MD calculations，the physical essence of microvoids evolution can be provided for larger-scale calculation. This article focuses on the application of MD simulation in the microvoids evolution of advanced materials. Starting from the current research status at home and abroad， the current research hot spots and key conclusions are summarized， and some problems existing in current MD simulation are analyzed.The development trend of related research in the future is prospected.

Keywords： microvoids evolution; molecular dynamics; advanced materials; atomic details