桥式起重机系统的传感故障容错控制研究

杨亚娜 霍俊红 产佳

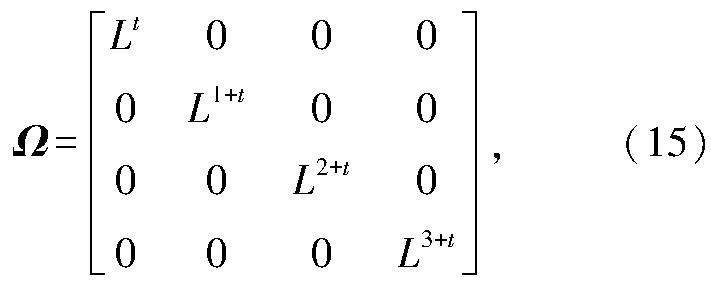
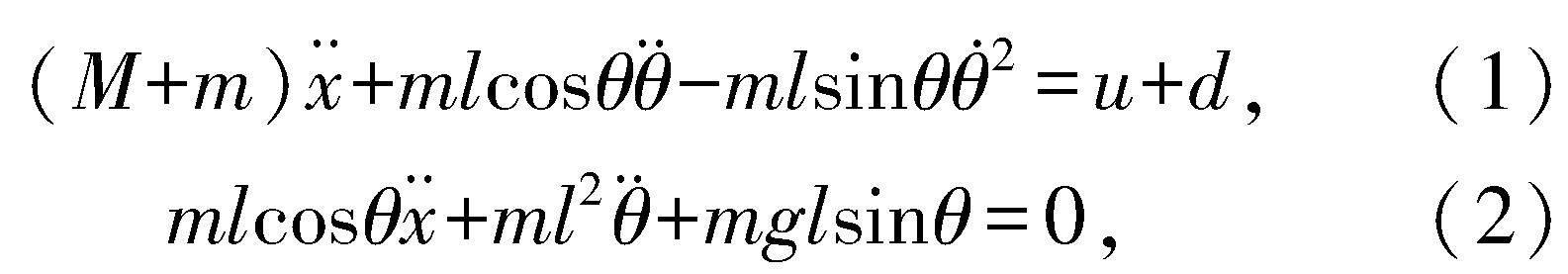
摘要：针对欠驱动桥式吊车系统的小车位置传感器故障问题，设计了一种基于观测器的自适应容错控制算法。考虑小车位置传感器出现了大小和符号均未知的故障，为了实现系统稳定下的定点和防摆控制目标，提出了由基于K滤波器的观测器以消除未知传感器故障的影响，同时引入Nussbaum增益来减轻故障未知符号的影响，二者共同组成自适应容错控制器使得桥式起重机可在传感器故障下依然实现控制目标。同时，基于李雅普诺夫稳定性理论，利用反步法证明了欠驱动桥式起重机系统的稳定性。最后，利用MATLAB验证了控制方案的可行性。

关键词：欠驱动桥式起重机；传感器故障；自适应容错控制；K滤波器

中图分类号： TP273文献标识码： ADOI：10.3969/j.issn.1007-791X.2024.02.0030引言

桥式起重机又称天车，是现代工业中的重要运输机械，因其承载能力强、省时省工且结构简单的优点，目前已广泛应用于仓库、车间、海港等工业现场货物的装载和运输[1-2]。但是桥式起重机作为典型的欠驱动系统，其控制变量维数少于所需控制系统自由度的维数，并且桥式起重机在运行过程中极易受到外界因素的影响，这些无疑给控制方案的实施带来困难[3]。

目前，在实际工作中，大多数起重机仍采用手动操作，这不仅导致小车的位置不够准确，而且难以抑制负载的摆动。负载的摆动会严重影响桥式起重机的运行，这不仅会降低工作精度，甚至还增加了事故发生的可能性[4]。因此，实现桥式起重机系统的高性能自动控制具有重要意义。近些年，越来越多的研究者们致力于设计既能跟踪小车位置又可以抑制摆角的控制算法。文献[5]通过在轨迹规划的基础上引入防摆机构来抑制摆角。文献[6]在拉格朗日方程的基础上建立了桥式起重机运动的非线性数学模型，并提出了一种桥式起重机消摆控制方法。文献[7]利用迭代学习控制重复运行的特性来对桥式起重机进行定位跟踪，并有效地抑制了负载摆角。文献[8]提出了输入整形控制，该方案可有效抑制摆角。文献[9]设计了基于模糊自适应PID控制的桥式起重机防摇控制器，使得小车位移和负载摆角都达到最优。此外，智能控制[10-12]，滑模控制[13-14]等控制方案也被提出来应用到起重机系统的控制中。上述研究方案都取得了一定的效果，但是，桥式起重机一般应用于工业现场，工作环境相对恶劣，许多不可控事件的发生将会对小车位置传感器造成负面影响，进而导致一系列控制方案效果变差甚至失效，因此，在桥式起重机系统控制中考虑传感器故障很有必要。

近年来，研究学者们在故障处理问题上投入了大量的精力[15]，但由于传感器故障很难被检测和补偿[15]，目前的研究主要集中在执行器故障上。因此，设计容错控制器以确保系统在传感器故障下仍然可以稳定运行是一项重要且具有挑战性的工作。文献[16]针对交互机器人提出了一种传感器故障诊断方案。文献[17]对输出带有不确定性的Lipschitz非线性系统，提出了一种自适应观测器的设计方法。然而，上述研究只是进行了故障诊断，并未对系统进行容错控制。文献[18]针对具有传感器故障的冷带轧机液壓厚度控制系统，提出基于自适应补偿机制的反步控制策略。文献[19]设计了基于学习观测器[20]的容错控制器对机械臂系统进行控制。文献[21]对一类输出含有未知参数的非线性系统设计了基于K滤波器的自适应容错控制器。桥式起重机在工业上被广泛应用，但因其工作环境的恶劣，传感器故障时有发生，容错控制技术可以有效处理系统发生的故障，进而保证系统的安全性和可靠性。但是，现有的针对桥式起重机的研究方案鲜有考虑传感器故障。另外，桥式起重机作为一个典型的欠驱动系统，很难将上述控制方案直接应用到该系统上。

针对上述问题，本文为小车位置传感器发生传感器故障的桥式起重机设计了一个基于K滤波器的自适应容错控制方案。借助坐标变换，该自适应容错控制方案适用于欠驱动桥式起重机系统，并能达到起重机在传感器故障下实现预设的定位及防摆控制的目的。本文的主要贡献为：设计基于K滤波器思想[21-22]的观测器以解决起重机的未知传感器故障问题，与现有的观测器算法相比，建立的基于K滤波器的观测器可仅利用具有不准确输出信息构造出不可测的状态变量。通过引入动态增益，该算法可以调整重构状态变量的收敛速度，提高系统的鲁棒性。同时利用Nussbaum函数来降低未知参数对控制系统设计的影响。最后利用反步法设计基于观测器和Nussbaum增益的控制器，实现了传感器故障下桥式起重机的定位控制。本文利用李雅普诺夫理论证明了该控制方案下桥式起重机系统的稳定性，并通过MATLAB验证了该方案的可行性。

1欠驱动桥式起重机系统模型

桥式起重机的简易模型如图1所示，可知其是一个典型的动力学模型，对其采用拉格朗日方程建立数学模型如下：

其中，M为小车的质量，m为负载的质量，l为钢绳的长度，θ为负载与垂直方向的夹角，x为小车的位置，u为起重机系统的控制输入，d为摩擦和负载力矩的总和，g表示重力加速度。

根据式（2）可得到下列关系式：

将式（3）代入式（1）中，可得

其中，

将系统输出定义为y=δz1，然后考虑τ=ξu以及=η+ξd，从而式（5）可以改写为

在这里考虑故障δ是完全未知的，即大小和符号都不确定。变换后的系统（5）由于存在非线性项（非线性项中可包含未知参数），本文将利用以下假设：

假设1若非线性系统中含有非线性项ω那么存在一个C1函数f*（z1）≥1和一个未知常数*≥1满足

|ω|≤*f*（z1）|z1|，（7）

又若y=δz1，上述式子可以等价为

其中，是依赖*的未知参数。

2控制器的设计

2.1基于K滤波器的观测器

首先将式（5）中的非线性项舍弃，进行观测器和动态增益的设计。

由于系统的输出y中含有未知参数δ，传统的非线性观测器均不能用，本文将学习K滤波器的思想，考虑以下观测器：

和

其中，κ=［κ1，κ2，κ3，κ4］T和γ=［γ1，γ2，γ3，γ4］T为由可测信号y和τ产生的K滤波器状态。L为动态增益（下文中将会进行设计），常实数ai>0，i=1，2，3，4为赫尔维茨多项式的系数。

使用上述观测器的状态（κ，γ）定义一个新的变量来估计：

考虑到桥式吊车系统（6）输出中含有未知传感器故障δ，定义误差变量

ei=δzi-（κi+δγi），（12）

将观测器（7）～（8）与上述误差相结合，可得到误差动力学系统：

其中，ι是一个常实数。

然后给出定义ν=［v1，v2，v3，v4］T=Ω-1e，其中，e=［e1，e2，e3，e4］T，

設计矩阵A为

此时可以得出变换后的误差动力学方程[23]为

其中，Wι=diag{ι，1+ι，2+ι，3+ι}。

考虑一个正定对称矩阵Q满足ATQ+QA

Vν=νTQν，（18）

易得式（18）的一阶导数为

为实现误差动力学系统的稳定，设计动态增益L为

其中，α（参数）和μ（y）（光滑函数）需要被设计。因为Q=QT>0，存在正常数ι，g1和g2满足

g1I

联系式（20），易得

从式（23）中可以很容易地看出，因非线性项的存在，设计的由非线性K滤波器（9）～（10）和动态增益更新定律（20）组成的观测器不可以渐近地估计系统状态，估计误差e不能趋于零。进而进行以下证明。

2.2稳定性证明

定理1基于假设1，存在一个由观测器（9）～（10），自适应控制器组成的自适应输出反馈控制器，使得存在传感器故障的起重机系统的状态z可以收敛，并且闭环系统的所有解都是有界的。即可实现桥式起重机的定位控制和防摆控制。

证明为了解决桥式起重机系统中小车位置传感器发生未知故障导致的系统输出参数未知问题，本文将设计两个自适应律分别对系统输出中的δ和进行自适应估计。

了解决未知传感器故障δ对系统稳定性的影响，本文在虚拟控制器中引入一个Nussbaum增益[24]，虚拟控制器具体形式如下：

针对式（24），系统基于上述思想，选取如下李雅普诺夫函数：

联系式（24）～（25）以及误差变换式（14），李雅普诺夫函数（26）的一阶导数可表示为

此时，设计自适应律以及所需函数ρ（·）为

从而可得

为了简化书写，本文设计：

根据式（27）和（31），式（32）的一阶导数可表示为

根据上述式子，设计虚拟控制器为

将式（34）和（35）相联系可得

Step 3：接下来的证明步骤与Step 2中相似，将进行适当简化。首先考虑

然后选择李雅普诺夫函数为

根据上式设计虚拟控制器：

则

Step 4：设计控制器。

同样考虑

选择李雅普诺夫函数为

则式（43）的一阶导数为

此时设计自适应律：

将式（45）和（46）联系起来，可得

为证明系统稳定性和系统状态有界，考虑以下李雅普诺夫函数：

V=5Vν+V4，（48）

其一阶导数为

将式（49）两边积分，

可以看出，无论δ<0还是δ>0，当m→∞时式（50）和（52）相矛盾，因此可以得出β在（0，Tf]一定有上界。

选择t=tjm，j=3，4，并将上式两边同时除β（tjm），易知

可以看出，无论δ<0还是δ>0，当m→∞时式（53）和（54）相矛盾，因此可以得出β在（0，Tf]一定有下界。

通过上述分析可以得出β在（0，Tf]有界。从上文式（48）和（52）可知（ν，y，γ2，）在（0，Tf]上有界，通过y有界和式（20）可知L在（0，Tf]上有界。又因为ν有界可知e在（0，Tf]上也有界。

从而可知κ和γ有界。综上所述，闭环系统所有状态有界。联系文中的坐标变换以及闭环系统状态有界，并运用Barbalat引理可以得出状态（z，κ，γ）均可实现收敛。这也就意味着起重机可以通过该控制方案实现定位控制，起重机的摆角也能被抑制。

综上可知，从理论分析上看，当动态增益L可以选取为无穷大时，则可以实现无穷大传感器故障的精确估计，但是由于受实际物理条件的限制，L的值的选取范围是有限的，因此只能实现对有限传感器故障的估计。当故障值较小时，可以很容易通过选取较小的L值实现对故障的估计。

3仿真结果

考虑小车位置传感器发生故障δ=0.9，使得小车位置测量值与实际值产生偏差。设计小车的理想位置xd=5 m（图2中的虚线），当传感器发生故障后的测量值与理想位置会有一定的偏差，实线则展示了经过容错控制后的小车的位移值，可以明显看到，经过容错控制器，小车的容错测量值与理想位置在t=4 s后基本保持一致，这也表明了本文设计控制方案的有效性。

时负载摆角情况如图3所示，可以观察到摆角前期最大值约为1.23°，但很快可以基本稳定在竖直方向上，表明该控制方案实现了对摆角的抑制，能够达到实际运行要求。

图4和图5则展示了δ=0.8，xd=8 m时小车位置轨迹容错后与理想位置的对比以及负载摆角情况，可以观察到小车的容错测量值与理想位置在t=3.8 s后基本保持一致，摆角前期最大值约为4.7°，但很快可以基本稳定在竖直线上，图4和图5也表明该控制方案的有效性，能够达到实际运行要求。

对比图2、3和图4、5，不难发现，起重机发生传感器故障后，无论传感器故障值为0.9还是0.8，在容错控制方案下，桥式吊车系统的小车在3.5 s后都能到达理想的位置，且定位控制的跟踪误差均在很小范围内；起重机的摆角在0.5 s后也均能基本维持稳定在竖直方向上，实现预期的要求。

故障值选为0.9或者0.8，从仿真结果中并看不出太大的区别。但是当故障值较大时，如果动态增益L仍选取原先的值，则故障估计精度就会较差。此时需要重新调整L的值，来获得令人满意的故障估计精度。

图6、7展示了xd=8 m时文章用到觀测器的状态值，图8则展现了本文所设计的两个自适应参数的估计值。

4结论

本文针对存在传感器故障的欠驱动桥式起重机设计了一种自适应容错控制方案。通过严格的李雅普诺夫证明，可以得出闭环系统所有状态都是有界的。基于K滤波器的观测器可以对未知故障进行处理，同时Nussbaum增益可以减轻故障未知符号的影响。由二者组成的自适应容错控制器可以使得桥式起重机在发生故障时依然能到达理想位置，同时使得负载摆角尽可能的小。

参考文献

[1] 朱发渊，汪朝晖，李欣欣.桥式起重机定位和消摆的非线性优化PID控制研究 [J].制造业自动化，2014，36（24）：76-79.

ZHU F Y，WANG Z H，LI X X.Research on nonlinear optimal PID control for positioning and damping of bridge crane [J].Manufacturing Automation，2014，36（24）：76-79.

[2] 王伟，易建强，赵冬斌，等.基于滑模方法的桥式吊车系统的抗摆控制[J].控制与决策，2004，19（9）： 1013-1016.

WANG W，YI J Q，ZHAO D B，et al.Anti-swing control of overhead cranes based on sliding-mode method[J].Control and Decision，2004，19（9）： 1013-1016.

[3] RAMLI L，MOHAMED Z，ABDULLAHI A M，et al.Control strategies for crane systems： a comprehensive review [J].Mechanical Systems & Signal Processing，2017，95： 1-23.

[4] 张圆圆，何永玲，周海燕，等.基于模糊变结构控制的桥式起重机防摆研究[J].中国工程机械学报，2019，17（2）：112-116.

ZHANG Y Y，HE Y L，ZHOU H Y，et al.Research on anti-swing of bridge crane based on fuzzy variable   structure control [J].Chinese Journal of Construction     Machinery，2019，17（2）：112-116.

[5] SUN N，FANG Y，ZHANG Y，et al.A novel kinematic coupling-based trajectory planning method for overhead cranes[J].IEEE/ASME Transactions on Mechatronics，2012，17（1）：166-173.

[6] 欧阳慧珉，张广明，王德明，等.基于S型曲线轨道的桥式起重机最优控制[J].振动与冲击，2014，33（23）：140-144.

OUYANG H M，ZHANG G M，WANG D M，et al.Optimal control of bridge crane based on S-curve track [J].   Vibration and Shock，2014，33（23）：140-144.

[7] 付子义，袁海国，王艺龙.基于迭代学习控制的桥式起重机定位及防摆[J].实验室研究与探索，2017，36（2）：34-38.

FU Z Y，YUAN H G，WANG Y L.Positioning and anti-swing of bridge crane based on iterative learning   control [J].Laboratory Research and Exploration，2017，36（2）：34-38.

[8] RAMLI L，MOHAMED Z，JAAFAR H I.A neural network-based input shaping for swing suppression of an overhead crane under payload hoisting and mass variations[J].Mechanical Systems and Signal Processing，2018，107：484-501.

[9] 罗宇鹏.桥式起重机防摇控制系统设计与实现[J].自动化应用，2020（12）：24-26.

LUO Y P.Design and realization of anti-roll control systemfor bridge crane [J].Automation Application，2020（12）：32-26.

[10] 杨春燕.桥式起重机定位和防摆的RBF神经网络控制[J].中国科技论文在线，2011，6（4）：320-324.

YANG C Y.RBF neural network control for positioning and anti-swing of bridge Crane [J].China Science and Technology Papers Online，2011，6（4）：320-324.

[11] 何博，方勇纯，刘海亮，等.桥式起重机精准定位在线轨迹规划方法设计及应用[J].控制理论与应用，2016，33（10）： 1352-1358.

HE B，FANG Y C，LIU H L，et al.Precise positioning online trajectory planner design and application for overhead cranes[J].Control Theory & Applications，2016，33（10）： 1352-1358.

[12] TUAN L A.Neural observer and adaptive fractional-order backstepping fast-terminal sliding-mode control of RTG cranes[J]，IEEE Transactions on Industrial Electronics，2021，68（1）：434-442.

[13] CHEN L，VAN M.Sliding mode control of a class of underactuated system with non-integrable momentum[J].Journal of the Franklin Institute，2020，357（14）：9484-9504.

[14] 梁慧慧，吴炜，楼旭阳，等.二维桥式起重机的滑模控制[J].控制与决策，2022，37（8）： 2163-2169.

LIANG H H，WU W，LOU X Y，et al.Sliding mode control of two-dimensional bridge crane [J].Control and Decision，2022，37（8）： 2163-2169.

[15] 张昭，李风雷，田琦.T-S模糊神经网络在风机故障诊断中的应用 [J].燕山大学学报，2016，40（4）： 336-341.

ZHANG Z，LI F L，TIAN Q.Application of T-S fuzzy neural network in fan fault diagnosis [J].Journal of Yanshan University，2016，40（4）： 336-341.

[16] 姜浪朗，张敬超，江国乾，等.基于超声解调信号多特征融合的轴承故障识别 [J].燕山大学学报，2022，46（6）： 484-491.

JIANG L L，ZHANG J C，JIANG G Q，et al.Bearing fault recognition based on ultrasonic demodulation signal multi-feature fusion [J].Journal of Yanshan University，2022，46（6）： 484-491.

[17] CHEN C，QIAN C，SUN Z，et al.Global output feedback stabilization of a class of nonlinear systems with unknownmeasurement sensitivity [J].IEEE Transactions on Automatic Control，2017，63（7）：2212-2217.

[18] CACCAVALE F，MARINO A，PIERRI F.Sensor fault diagnosis for manipulators performing interaction tasks [C]//2010 IEEE International Symposium on Industrial Electronics，Bari， Italy，2010：2121-2126.

[19] 邹伟，刘玉生.含未知参数和输出不确定性的Lipschitz非線性系统自适应观测器设计[J].四川大学学报（工程科学版），2014，46（5）：156-160.

ZHOU W，LIU Y S.Adaptive observer design for Lipschitz nonlinear systems with unknown parameters and output uncertainties[J].Journal of Sichuan University（Engineering Science），2014，46（5）：156-160.

[20] 王建波，王芳，华长春.基于故障补偿机制的冷轧厚控系统自适应反步控制 [J].燕山大学学报，2022，46（1）： 46-55.

WANG J B，WANG F，HUA C C.Adaptive backstepping control design for a HAGC system based on fault compensation mechanism [J].Journal of Yanshan University，2022，46（1）： 46-55.

[21] KANG Y，YAO L，WU W.Sensor fault diagnosis and fault tolerant control for the multiple manipulator synchronized controlsystem [J].ISA Transactions，2020，106：243-252.

[22] JIA Q，CHEN W，ZHANG Y，et al.Fault reconstruction for takagi-sugeno fuzzy systems via learning observers [J].International Journal of Control，2016，89（3）：564-578.

[23] XU Z A，WEI L.A K-filter-based adaptive control for nonlinear systems with unknown parameters in state and outputequations[J].Automatica，2019，105：186-197.

[24] GAO R，HUANG J，SU X，et al.K-filter-based adaptive output feedback control for high-order nonlinear systems subject to actuator and sensor attacks[J].International Journal of Robust and Nonlinear Control，2022，32（6）： 3469-3484.

[25] HAO L，WEI L.Adaptive regulation of uncertain nonlinear systems by output feedback： a universal control approach[J].Systems & Control Letters，2007，56（7）：529-537.

[26] CHEN Z.Nussbaum functions in adaptive control with time-varying unknown control coefficients[J].Automatica，2019，102： 72-79.

Research on sensor fault tolerant control for bridge crane system

Abstract： In this paper，an adaptive faulttolerant control algorithm based on observer is designed for the fault of trolley position sensor in underdrive bridge crane system.Considering the trolley position sensor occurs an unknown fault，in order to achieve the fixed point control goal under the stability of the system，an observer based on K filter is proposed to eliminate the influence of unknown sensor faults，and Nussbaum gain is introduced to reduce the influence of unknown symbols of faults.The adaptive faulttolerant controller is composed of the above two parts so that the bridge crane can achieve the control target even under sensor faults.At the same time，based on Lyapunov stability theory，the stability of underdrive bridge crane system is proved by backstepping method.Finally，the feasibility of the control scheme is verified by using MATLAB.

Keywords： underdrive bridge crane; sensor fault; adaptive fault tolerant control; K filter