基于聚类与稀疏字典学习的近似消息传递

司菁菁 王亚茹 王爱婷 程银波

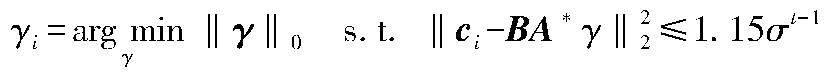
摘要：基于传统字典学习的近似消息傳递（approximate message passing，AMP）算法对训练样本数量的需求较高，且运算成本较高。本文引入双稀疏模型，构建基于稀疏字典学习的AMP框架，降低迭代过程中字典学习对训练样本数量的需求，提高压缩感知图像重建的质量与效率。进一步，提出基于聚类与稀疏字典学习的AMP算法，在迭代过程中依据图像块特征进行分类，并为各类图像块分别学习稀疏字典，实现自适应去噪。与基于传统字典学习的AMP算法相比，基于聚类与稀疏字典学习的AMP算法能够将重建图像的峰值信噪比提高0.20～1.75 dB，并且能够将运算效率平均提高89%。

关键词：图像重构；近似消息传递；字典学习；稀疏字典；聚类

中图分类号：TN911.73文献标识码： ADOI：10.3969/j.issn.1007-791X.2024.02.006

0引言

压缩感知（compressed sensing，CS）[1-2]突破了奈奎斯特采样定理的限制，能够同时实现稀疏信号或可压缩信号的采样与压缩，并可以从欠采样的测量数据中准确地重构出原始信号[3]。该理论一经提出便引起学术界及工业界的广泛关注。

自然图像中含有大量冗余信息，可有效地进行稀疏表示。若利用CS将图像的采样和压缩同时进行，则可以在不牺牲图像重建质量的前提下，大大简化图像处理系统采样端的硬件结构并降低存储设备的容量。重构算法是基于CS的成像过程的核心研究内容之一。

近似消息传递（approximate message passing，AMP）[4]是一种基于迭代阈值的CS重构算法，具有收敛速度快、运算复杂度低等优点，能够利用少量的线性测量值恢复稀疏信号，非常适用于图像重建等大数据量应用领域。当将AMP应用于图像重建时，迭代过程中滤波操作的设计与实现及其对信号结构特征的利用能力，在很大程度上影响着整个重建算法的性能。

图像在小波域上的稀疏性是现有的基于AMP的图像重构算法常用的先验信息[5]之一。文献[6]将振幅不变贝叶斯估计与小波域自适应Wiener滤波应用到AMP框架中，提出了AMP-ABE和AMP-Wiener两种图像重建算法。文献[7]提出了基于小波域Cauchy先验的AMP算法。此外，针对小波域稀疏先验不适用于包含较多非平滑信息图像的问题，文献[8]提出了利用梯度稀疏先验保留图像边缘和纹理信息的AMP算法。文献[9]提出了基于去噪的AMP （denoising based approximate message passing，DAMP），在AMP的迭代过程中，利用BM3D[10-11]等经典变换域图像去噪算子实现滤波，获得了较高的图像重建性能。

设计与待滤波信号稀疏特性相匹配的去噪算子是提高DAMP图像重建性能的关键。字典学习是实现图像去噪的一种有效技术[12-13]。基于MOD （method of optimal directions）、K-SVD （K-means singular value decomposition）[14-16]和SGK （sequential generalization of K-means）[17]等字典学习算法实现的图像去噪具有优于小波域图像去噪算子的性能。文献[18]将字典学习与AMP相结合，提出了基于字典学习的AMP （dictionary learning based AMP，DL-AMP），在迭代过程中利用字典学习实现图像去噪，能够获得优于基于固定变换域去噪算子的DAMP的图像重建性能。

然而，训练数据的数量直接影响着K-SVD等字典学习算法的性能。在DL-AMP的每次迭代中，字典学习算法可用的训练数据完全来源于当前待滤波信号，数量非常有限。这就使得K-SVD等字典学习算法能够实现的去噪性能受到了限制。另一方面，K-SVD等字典学习算法的运行时间较长，而在DL-AMP的每次迭代中需要完整运行两次字典学习算法，使得DL-AMP的运行时间较长。

针对上述问题，本文将基于稀疏字典进行图像稀疏表示的双稀疏模型[19]引入AMP，研究基于稀疏字典学习的AMP （sparse dictionary learning based AMP，SDL-AMP），降低字典学习对训练样本数量的需求，提高重建质量。此外，为了进一步提高稀疏字典学习的效率与去噪性能，本文提出了基于聚类与稀疏字典学习的AMP （clustering and sparse dictionary learning based AMP，CSDL-AMP），在迭代过程中依据图像块特征进行分类，并为各类图像块分别学习稀疏字典，实现自适应去噪。仿真实验结果表明，与基于固定变换域去噪算子的DAMP相比，SDL-AMP和CSDL-AMP具有明显提高的图像重建性能；与DL-AMP相比，SDL-AMP和CSDL-AMP不但具有较高的图像重建性能，而且具有显著提高的运算效率。

1基础算法

y=Φx+ω，（1）

式中，ω∈RM表示测量噪声，其中元素符合高斯分布N（0，σ2）。

现有的DAMP方案多采用BM3D等经典图像去噪算法实现固定的Dσt－1（·）。若能够在每次迭代中依据当前待滤波信号xt－1+ΦTzt－1的特征，自适应地调整Dσt－1（·），则有望进一步提高DAMP的重建性能。

DL-AMP将基于字典学习的图像去噪引入DAMP框架，在迭代过程中依据当前待滤波信号xt－1+ΦTzt－1进行字典学习，利用图像信号x可以进行稀疏表示而噪声vt－1却不能的特性实现去噪。DL-AMP的第t次迭代可以表示为

式中，DL（·）表示基于字典学习的图像去噪子，以待滤波信号xt－1+ΦTzt－1、噪声标准差σt－1和初始字典Dt－1为输入，输出滤波结果xt与训练出的字典D*t-1。DL′（·）表示DL（·）的求导运算，以xt－1+ΦTzt－1、σt－1和初始字典D*t-1为输入，输出divt与二次训练出的字典D**t-1，其中

与DAMP相比，DL-AMP能够进一步提高重建图像的质量。然而，训练数据的数量直接影响着K-SVD等字典学习算法的性能。在DL-AMP框架下，第t次迭代中能够用于字典学习的训练数据完全来源于待滤波信号xt－1+ΦTzt－1，数量有限。另一方面，由于K-SVD等字典学习算法的运算时间较长，且在DL-AMP框架下的每次迭代中需要进行D*t-1和D**t-1两个字典的训练，因此DL-AMP的实现速度较慢。针对以上问题，本文研究基于稀疏字典学习的AMP框架SDL-AMP，进而研究基于聚类与稀疏字典学习的AMP框架CSDL-AMP。

2基于稀疏字典学习的AMP框架

双稀疏模型假设字典D=d1，d2，…，dH∈RG×H能够在基字典B∈RG×P上进行稀疏表示，即D=BA，（11）式中，A=a1，a2，…，aH∈RP×H为稀疏表示矩阵，其中的第j列aj∈RP表示字典D中的第j个原子dj∈RG在基字典B上的稀疏表示向量。设任意列aj中非零元素的个数‖aj‖0≤p。与普通字典相比，稀疏字典具有更强的适应性，且更易于存储和传输。

以训练样本xi∈RG：i=1，2，…，U为列构成训练数据矩阵X∈RG×U。设X在如式（11）所示的字典D上是稀疏的，即X可稀疏表示为X=DΓ=BAΓ，（12）式中，Γ=γ1，γ2，…，γU∈RH×U为样本矩阵X在字典D上的稀疏表示矩阵，其中的第i列γi∈RH表示样本xi在D上的稀疏表示向量。设任意列γi中非零元素的个数‖γi‖0≤q。

稀疏字典的训练可以通过求解如下优化问题来实现：

式中，‖·‖F表示Frobenius范数。

本文将能够实现此优化问题近似求解的稀疏K-SVD字典学习算法总结为算法1，用于在本文设计的SDL-AMP框架与CSDL-AMP框架中实现基于稀疏字典学习的图像去噪算子SDL（·）。

算法1基于稀疏K-SVD字典学习算法实现的图像去噪算子SDL（·）

输入：信号矩阵X∈RG×U，基字典B∈RG×P，初始字典稀疏表示系数矩阵A0∈RP×H，目标原子稀疏度p，稀疏编码误差容限e，迭代次数K；

初始化：A=A0；

迭代过程：

For n=1，2，…，K do

1） 根据当前字典BA，更新信号矩阵X的稀疏表示矩阵Γ：

For i=1，2，…，U do

γi=argminγ‖γ‖0s.t. ‖xi－BAγ‖22≤e

End for

Γ=γ1，γ2，…，γU

2） 根据当前信号稀疏表示矩阵Γ，更新字典稀疏表示矩阵A：

For j=1，2，…，H do

aj=0

I={X中用aj参与表示的信号索引}；

g=ΓTj，I

g=g/‖g‖2

E=XI－BAΓI

z=Eg

aj=arg mina‖z－Ba‖22s.t.‖a‖0≤p，

aj=aj/‖Baj‖2

Γj，I=（XTIBaj－（BAΓI）TBaj）T

End For

End For

在算法1中，XI表示由信号矩阵X中序号在集合I中的列构成的矩阵；ΓI表示由系数矩阵Γ中序号在集合I中的列构成的矩阵；Γj，I表示矩阵ΓI中的第j行。与原始K-SVD字典学习算法相比，稀疏K-SVD字典学习对样本数量的需求明显降低[19]。

本文将稀疏字典学习引入AMP，研究基于稀疏字典学习的AMP框架SDL-AMP，具体设计了基于稀疏K-SVD字典学习的AMP算法SK-SVD-AMP，如算法2所示。

算法2SK-SVD-AMP算法

输入：测量值向量y∈RM，测量矩阵Φ∈RM×N，迭代次数L，块尺寸B，分块步长S，基字典B∈RG×P，初始字典稀疏表示系数矩陣A0∈RP×H，目标原子稀疏度p，稀疏K-SVD迭代次数K；

迭代过程：

For t=1， 2，…，L do

1） qt－1=xt－1+ΦTzt－1

Q*=Vector2Matrix（qt－1）

C*=BlockDivide（Q*，B，S）

2） 利用算法1实现基于稀疏字典学习的去噪：

（C**，A*）=SDL（C*，B，At－1，p，1.15σt－1，K）

Q**=BlockMerge（C**，B，S）

xt=Matrix2Vector（Q**）

3） 生成随机向量b∈RN，其中任意元素符合标准正态分布；令τ=‖qt－1‖∞/1 000；

Q*=Vector2Matrix（qt－1+τb）

C*=BlockDivide（Q*，B，S）

4） 利用算法1实现基于稀疏字典学习的去噪：

（C**，At）=SDL（C*，B，A*，p，1.15σt－1，K）

Q**=BlockMerge（C**，B，S）

x*=Matrix2Vector（Q**）

5） divt=bT（x*－xt）/τ

在算法2的每次迭代中，步骤1）～2）利用基于稀疏K-SVD字典学习的去噪算子SDL（·）实现信号xt的估计；步骤3）～5）利用Monte Carlo技术[20]实现divt的计算；步骤6）～7）计算残差并估计其标准差。X=Vector2Matrix（x）表示将向量x∈RN排列成矩阵形式X∈RN×N；x=Matrix2Vector（X）表示相反的操作，即将矩阵X∈RN×N还原成向量形式x∈RN。C=BlockDivide（X，B，S）表示以B×B为块尺寸、S为步长，对矩阵X进行重叠分块，并将每个块中的元素排列成列向量，组合成矩阵C；X=BlockMerge（C，B，S）表示相反的操作，即将矩阵C中的每一列还原成B×B的块，以S为步长、利用重合平均的方式融合成矩阵X。‖·‖∞表示∞-范数。

与DL-AMP相比，本文设计的SDL-AMP算法SK-SVD-AMP在迭代过程中利用稀疏字典学习实现图像去噪，降低了对训练样本数量的要求，且在每次迭代中训练出的字典更符合待滤波信号的结构特征。

3基于聚类与稀疏字典学习的AMP方案

为了进一步提高稀疏字典学习的效率与基于稀疏字典学习的去噪算子的自适应性，本文将聚类引入SDL-AMP，研究基于聚类与稀疏字典学习的AMP框架CSDL-AMP，并具体设计了基于K-means聚类与稀疏K-SVD字典学习的AMP算法CSK-SVD-AMP，如算法3所示。

算法3CSK-SVD-AMP算法

输入：测量值向量y∈RM，测量矩阵Φ∈RM×N，迭代次数L，块尺寸B，分块步长S，基字典B∈RG×P，初始字典稀疏表示系数矩阵A0∈RP×H，目标原子稀疏度p，稀疏K-SVD迭代次数K，类别数量W；

迭代过程：

For t=1，2，…， L do

1） qt－1=xt－1+ΦTzt－1

Q*=Vector2Matrix（qt－1）

C*=BlockDivide（Q*，B，S）

2） 以均值为特征，利用K-means对C*中的列向量进行聚类，以属于第w类的列向量构成子矩阵Ptw，w=1，2，…，W。

3） 利用算法1分别对各子矩阵进行基于稀疏字典学习的去噪：

For w=1，2，…，W do

（C**w，Atw）=SDL（Ptw，B，At－1w，p，1.15σt－1，K）

End for

4） 将子字典At1，At2，…，AtW合并为一个总字典A*=At1，At2，…，AtW；

5） 将子矩阵C**w：w=1，2，…，W按照步驟2）中子矩阵划分的逆过程合并成矩阵C**；

Q**=BlockMerge（C**，B，S）

xt=Matrix2Vector（Q**）

6） 生成随机向量b∈RN，其中任意元素符合标准正态分布；令τ=‖qt－1‖∞/1 000；

Q*=Vector2Matrix（qt－1+τb）

C*=BlockDivide（Q*，B，S）

7） 利用字典A*对C*进行稀疏表示，实现去噪：

Col=矩阵C*中的列数；

For i=1，2，…，Col do

ci=C*中的第i列

End for

C**=BA*γ1，BA*γ2，…，BA*γCol

Q**=BlockMerge（C**，B，S）

x*=Matrix2Vector（Q**）

8） divt=bT（x*－xt）/τ

在算法3的每次迭代中，步骤1）～5）利用K-means对图像块进行聚类，并利用SDL（·）分别对各类图像块进行基于稀疏字典学习的去噪，实现信号xt的估计；步骤6）～8）利用Monte Carlo技术实现divt的计算，其中qt－1+τb的去噪利用基于当前已知字典A*的稀疏表示进行，而未进行二次字典学习；步骤9）～10）计算残差并估计其标准差。

与算法2相比，算法3中对图像块进行了聚类，并针对每类图像块分别进行了基于稀疏字典学习的去噪，能够提高字典学习的效率以及字典与图像块特征的匹配程度。

4实验结果分析

为了验证本文提出的SK-SVD-AMP算法和CSK-SVD-AMP算法的有效性，将它们与基于BM3D的DAMP算法BM3D-AMP、基于LRA_SVD的DAMP算法LRA_SVD-AMP[21]、基于FRIST的DAMP算法FRIST-AMP[22]、基于SNSS的DAMP算法SNSS-AMP[23]和基于K-SVD的DL-AMP算法K-SVD-AMP进行性能比较。在SK-SVD-AMP算法和CSK-SVD-AMP算法中，设置分块尺寸为8×8、步长为1，选用64×256的过完备离散余弦基作为基字典。

以128×128像素的Lake、Flinstones、Starfish、Crowd和Man等5幅标准灰度测试图像作为实验对象。仿真实验所用计算机的硬件配置为Intel Core i7-9700 四核 CPU、3.00 GHz主频、8 GB内存；软件环境为64位Windows 10系统下的MATLAB 2019b。以峰值信噪比（peak signal-to-noise ratio，PSNR）作为衡量算法重构性能的客观指标。

首先，分析迭代次数L对LRA_SVD-AMP、FRIST-AMP、SNSS-AMP、BM3D-AMP、K-SVD-AMP、SK-SVD-AMP和CSK-SVD-AMP七种算法重建性能的影响。图1以Flinstones图像为例，在不考虑测量噪声、采样率M/N=0.5、设置SK-SVD-AMP和CSK-SVD-AMP的目标原子稀疏度p分别为65和25的情况下，显示了七种算法重建图像的PSNR值随迭代次数的变化情况。如图1所示，在迭代次数达到20之后，七种算法获得的PSNR值均变化较小。在其他采样率、噪声水平、目标原子稀疏度设置下进行的实验均获得了相似的结果。因此，本文后续以迭代次数L=20为例，展示仿真实验结果。

然后，在不同测量噪声水平下，比较LRA_SVD-AMP、FRIST-AMP、SNSS-AMP、BM3D-AMP、K-SVD-AMP、SK-SVD-AMP和CSK-SVD-AMP七种算法获得的PSNR值。以重建Lake图像为例，设置SK-SVD-AMP和CSK-SVD-AMP的目标原子稀疏度p分别为65和25。图2、图3和图4分别在不考虑测量噪声、测量噪声方差σ2=10和σ2=20的情况下，展示了七种算法在不同采样率下获得的PSNR值。如图2～图4可见，在相同条件下，基于字典学习或稀疏字典学习的K-SVD-AMP、SK-SVD-AMP和CSK-SVD-AMP获得的PSNR值高于LRA_SVD-AMP、FRIST-AMP、SNSS-AMP和BM3D-AMP。在相同条件下，SK-SVD-AMP获得的PSNR值与K-SVD-AMP基本相当；CSK-SVD-AMP获得的PSNR值在大多数情况下高于K-SVD-AMP和SK-SVD-AMP。

接下来，比较LRA_SVD-AMP、FRIST-AMP、SNSS-AMP、BM3D-AMP、K-SVD-AMP、SK-SVD-AMP和CSK-SVD-AMP七种算法重建图像的主观视觉效果。图5以重建Lake图像为例，在不考虑测量噪声、采样率M/N=0.4、设置SK-SVD-AMP和CSK-SVD-AMP的目标原子稀疏度p分别为65和25的情况下，展示了七种算法的重建图像。如图5可见，七种算法重建图像清晰度由高到低的顺序依次为CSK-SVD-AMP、SK-SVD-AMP、K-SVD-AMP、FRIST-AMP、BM3D-AMP、LRA_SVD-AMP和SNSS-AMP。此外，比较七幅重建图像中的方框区域可见，CSK-SVD-AMP重建图像中的细节最清晰且最接近原图像。

最后，比较K-SVD-AMP、SK-SVD-AMP、CSK-SVD-AMP、LRA_SVD-AMP、FRIST-AMP和SNSS-AMP六种重建算法的运行时间。以在不考虑测量噪声的情况下重建Flinstones图像为例，在不同采样率下分别比较六种算法的运行时间。以采样率为0.7时K-SVD-AMP算法的运行时间为基准，表1显示了六种算法在不同采样率下的运行时间与该基准时间的相对值。由表1可见，在任意采样率下，CSK-SVD-AMP、SK-SVD-AMP和LRA_SVD-AMP的运行时间均远低于K-SVD-AMP、FRIST-AMP和SNSS-AMP。与SK-SVD-AMP、FRIST-AMP相比，CSK-SVD-AMP的运行时间更低。

综合以上实验结果可见，本文设计实现的基于稀疏字典学习的CSK-SVD-AMP算法和SK-SVD-AMP算法獲得的PSNR值明显高于基于固定变换域去噪算子的BM3D-AMP、FRIST-AMP、LRA_SVD-AMP和SNSS-AMP，且不低于基于字典学习的K-SVD-AMP。与BM3D-AMP、FRIST-AMP、LRA_SVD-AMP、SNSS-AMP和K-SVD-AMP相比，CSK-SVD-AMP和SK-SVD-AMP的重建图像中具有更清晰的细节信息。与K-SVD-AMP相比，SK-SVD-AMP和CSK-SVD-AMP的运算时间显著缩短。

5结论

本文将双稀疏模型引入AMP，构建了基于稀疏字典学习的SDL-AMP框架，获得了明显优于DAMP和DL-AMP的图像重建性能。进一步，提出了结合聚类与稀疏字典学习的CSDL-AMP方案，获得了优于DL-AMP的图像重建性能。仿真实验结果表明，与DL-AMP相比，CSDL-AMP能够将重建图像的PSNR值提高0.20～1.75 dB，且重建图像中保留了更清晰的图像细节。同时，CSDL-AMP的运行时间平均仅为DL-AMP运行时间的0.108倍。

参考文献

[1] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory， 2006， 52（4）： 1289-1306.

[2] GREL N M， KARA K， STOJANOV A， et al. Compressive sensing using iterative hard thresholding with low precision data representation：theory and applications[J]. IEEE Transactions on Signal Processing， 2020， 68： 4268-4282.

[3] KHOBAHI S， SOLTANALIAN M. Model-based deep learning for one-bit compressive sensing[J]. IEEE Transactions on Signal Processing， 2020， 68： 5292-5307.

[4] DONOHO D L， MALEKI A， MONTANARI A. Message-passing algorithms for compressed sensing[J]. Proceedings of the National Academy of Sciences of the United States of America， 2009， 106（45）： 18914-18919.

[5] SOM S， SCHNITER P. Compressive imaging using approximate message passing and a Markov-tree prior[J]. IEEE Transactions on Signal Processing， 2012， 60（7）： 3439-3448.

[6] TAN J， MA Y T， BARON D. Compressive imaging via approximate message passing with image denoising[J]. IEEE Transactions on Signal Processing， 2015， 63（8）： 2085-2092.

[7] HILL P R， KIM J H， BASARAB A， et al. Compressive imaging using approximate message passing and a Cauchy prior in the wavelet domain[C]//2016 IEEE International Conference on Image Processing，Phoenix， USA， 2016： 2514-2518.

[8] WANG X， LIANG J. Multi-resolution compressed sensing reconstruction via approximate message passing[C]// 2015 IEEE International Conference on Image Processing，Quebec， Canada， 2015： 4352-4356.

[9] METZLER C A， MALEKI A， BARANIUK R G. From denoising to compressed sensing[J]. IEEE Transactions on Information Theory， 2016， 62（9）： 5117-5144.

[10] DABOV K， FOI A， KATKOVNIK V， et al. Image denoising by sparse 3-D transform-domain collaborative filtering[J]. IEEE Transactions on Image Processing， 2007， 16（8）： 2080-2095.

[11] BASHAR F， EL-SAKKA M R. BM3D image denoising using learning-based adaptive hard thresholding[C]//Proceedings of the 11th Joint Conference on Computer Vision， Imaging and Computer Graphics Theory and Applications， Rome， Italy， 2016： 204-214.

[12] XUE S Y， YIN C， SU Y， et al. Airborne electromagnetic data denoising based on dictionary learning[J]. Applied Geophysics， 2020， 17（2）： 306-313.

[13] XU M R， HU D L， LUO F L， et al. Limited-angle X-ray CT reconstruction using image gradient 0-norm with dictionary learning[J]. IEEE Transactions on Radiation and Plasma Medical Sciences， 2021， 5（1）： 78-87.

[14] AHARON M， ELAD M， BRUCKSTEIN A. K-SVD：an algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing， 2006， 54（11）： 4311-4322.

[15] SCETBON M， ELAD M， MILANFAR P. Deep K-SVD denoising[J]. IEEE Transactions on Image Processing， 2021， 30： 5944-5955.

[16] 封常青， 李予國， 吴云具， 等. 利用K-SVD字典学习算法压制海洋大地电磁噪声[J]. 地球物理学报， 2022， 65（5）： 1853-1865.

FENG C Q， LI Y G， WU Y J， et al. A noise suppression method of marine magnetotelluric data using K-SVD dictionary learning [J]. Chinese Journal of Geophysics， 2022， 65（5）： 1853-1865.

[17] SAHOO S K， MAKUR A. Dictionary training for sparse representation as generalization of K-means clustering[J]. IEEE Signal Processing Letters， 2013， 20（6）： 587-590.

[18] LI Z C， HUANG H， MISRA S. Compressed sensing via dictionary learning and approximate message passing for multimedia internet of things[J]. IEEE Internet of Things Journal， 2017， 4（2）： 505-512.

[19] RUBINSTEIN R， ZIBULEVSKY M， ELAD M. Double sparsity：learning sparse dictionaries for sparse signal approximation[J]. IEEE Transactions on Signal Processing， 2010， 58（3）： 1553-1564.

[20] RAMANI S， BLU T， UNSER M. Monte-Carlo sure：a black-box optimization of regularization parameters for general denoising algorithms[J]. IEEE Transactions on Image Processing， 2008， 17（9）： 1540-1554.

[21] GUO Q， ZHANG C， ZHANG Y，et al. An efficient SVD-based method for image denoising[J]. IEEE Transactions on Circuits and Systems for Video Technology， 2016， 26（5）： 868-880.

[22] WEN B， BRESLER Y， RAVISHANKAR S. FRIST-flipping and rotation invariant sparsifying transform learning and applications[J]. Inverse Problems， 2017， 33（7）： 074007.

[23] ZHA Z， YUAN X， ZHOU J， et al. Image restoration via simultaneous nonlocal self-similarity priors[J]. IEEE Transactions on Image Processing， 2020， 29：8561-8576.

Clustering and sparse dictionary learning based

approximate message passing

Abstract： Dictionary learning based approximate message passing （AMP） has a high demand on the number of training samples， and its computational cost is high.The double sparse model is introduced to study sparse dictionary learning based AMP， which reduces the demand on the number of training samples in the iterations and improves imaging quality and efficiency. Furthermore， the clustering and sparse dictionary learning based AMP is proposed. In iterations， the clustered blocks are denoised adaptively with sparse dictionary learning. In comparison to traditional dictionary learning based AMP， the clustering and sparse dictionary learning based AMP can achieve 0.20～1.75 dB higher peak signal-to-noise ratio of the reconstructed images， and improve the computational efficiency by 89% in average.

Keywords： image reconstruction; approximate message passing; dictionary learning; sparse dictionary; clustering