形成度量结构 发展量感与应用意识
——“角的度量”单元教学设计与实践
2024-05-02北京市通州区教师研修中心刘东旭
北京市通州区教师研修中心 刘东旭
北京第二实验小学通州分校 晁倍倍
北京市通州区张家湾镇中心小学 王 颖
指导教师:北京教育科学研究院 刘延革
在图形长度、周长与面积的学习中,学生两次经历“辨别度量属性、确立度量单位、使用工具测量或公式计算、得到度量结果(解决问题)”的认知过程。“角的度量”单元学习是学生在此基础上,进一步深化对度量要素(对象、单位、工具与结果)的理解,感受知识之间的一致性,完善度量的认知结构,并能自主迁移到体积等度量内容的学习中。文章基于北京团队开发单元整体设计框架 ,对“角的度量”单元设计的重要环节与教学实践进行阐述。
一、单元具体概念及主题
(一)教材分析
“角的度量”单元内容包括角的度量、角的分类与画角,对比人教版、北师大版和北京版小学数学教材(见表1),我们发现:
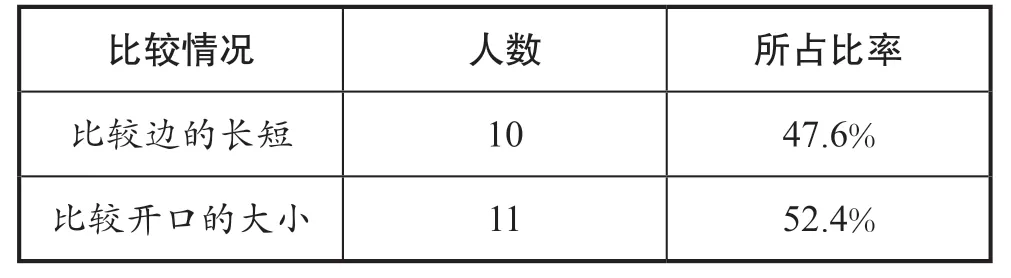
表1 追踪调研结果
1.在比较中明确度量对象
度量刻画的是事物属性的“大小”,教学时需要设计活动帮助学生体会事物可以被测的属性。人教版数学教材中创设了两个角的大小比较情境,相较于其他两个版本,我们认为学生会在“比较”中更加关注“比哪里”,更能突出度量对象的属性。
2.在交流中统一度量单位
度量单位的产生和发展经历从多元到统一、由粗略到精细的过程,北师大版教材引领学生经历“非标准单位—标准单位—细化单位—统一单位”的过程。学生经历“角的度量单位是小角”的探索过程,然后创造或选择合适的度量单位来进行量化,通过对比和交流最终统一度量单位,更加有助于感悟“度量单位”产生的意义。因为用非标准单位测量不仅能够让学生体会单位或标准的作用,感受统一单位的必要性,还能培养学生的创造性和迁移能力。
3.在动态中理解量角器的构造原理
量角器是度量单位的集合,理解其构造原理是学习的难点。我们借鉴北师大版教材的活动,将10°和30°作为标准小角,学生通过数一数、估一估、画一画和剪一剪,经历由“一个单位”的标准延伸至“几个单位”的累加,感受到量角的一般方法是统一小角的不断累积。因此,我们设计用“单位”量角不方便的情境,引导学生迁移用直尺测量长度的经验,进而在创造量角器的过程中理解其构造原理。
4.在应用中体会工具的价值
三个版本的教材都呈现了丰富的量角和画角活动,但缺乏接近生活的现实情境。教学中,我们认为要注重将量角、画角与生活实际相结合,同时提供多元的量角工具,深化学生对工具价值的感悟。此外,新课标中强调“估测”对发展量感的价值,教学中需关注“估”与“测”的有机融合。
(二)单元具体概念及学习主题
基于上述分析,结合“图形与几何”领域的核心概念,我们归纳了四条“单元具体概念”,并将本单元学习主题定位为“形成度量结构 发展学生量感和应用意识”。
具体概念一:角的度量是对角的两条边张开大小的刻画。
具体概念二:量角的一般方法是统一小角的不断累积;将多个小角组合在一起产生了量角器,使得测量更加方便。
具体概念三:根据实际情况选取量角和画角的方法和工具。
具体概念四:在上述活动中,丰富学生的度量经验,发展学生量感和应用意识。
二、学情调研及单元学习目标
在上述分析的基础上,我们对北京某校四年级52名学生进行调研。
(一)学情调研
1.调研题目及调研目的
(1)请你量一量下面这个角有多大。
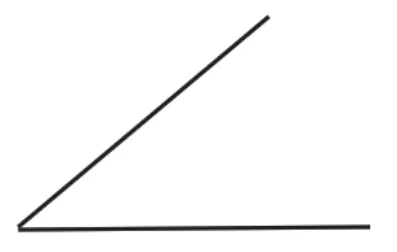
①你打算量哪里?请先在图中标出来。
②你选择的工具是______,测量的结果是______。
目的:了解学生是否明确量哪以及是否清楚用什么量角。
(2)请你用量角器画一个35°的角,说一说你是怎么画的。
目的:了解学生是否能迁移量角经验,用量角器画角。
2.调研结果
(1)学生对“量哪”存在认知偏差。
明确度量对象是学习度量的前提,调研结果发现:46.7%的学生量边的长度,53.3%的学生量开口的位置。由此可见,近一半的学生不知道量角要“量哪里”。为更准确地把握情况,我们对量边的21 名学生进行追踪调研(如图1),发现有11 名学生关注角的开口大小(见表1)。因此,我们认为在比较活动中,学生会更加清楚角的大小指哪里。
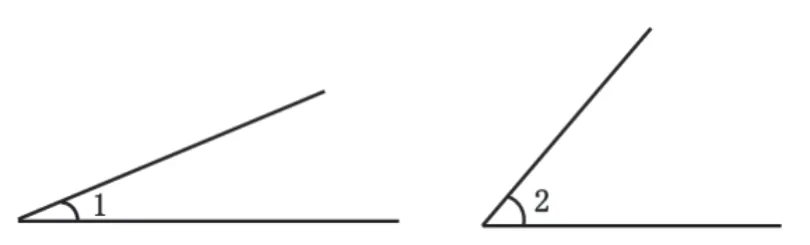
图1
(2)学生对“用什么量”缺少直接经验。
对度量工具的选择,77.8%的学生用直尺,6.8%的学生用三角尺。结合访谈,我们发现学生认为“三角尺上有角”,意识到要用同属性的物体测量,但并不清楚具体的量角工具。15.5%的学生选择量角器,其中1 名学生能准确测量,但并不清楚为什么要这么量。因此,我们认为教学中需要让学生经历量角器产生的过程,加深对度量工具的认识。
(3)学生对“为什么要这么量”认识不到位。
通过观察,我们发现学生在使用量角器时,主要出现了以下错误:一是将角的顶点与量角器的一端重合;二是用量角器曲边上的“刻度线”表示角的张口大小,缘于测量长度的经验所带来的负迁移。以往教学中我们同样发现学生机械套用“二合一看”的步骤,当测量倾斜摆放的角时正确率低,读数时混淆量角器两圈的刻度等。因此,理解“为什么要这么量”,即理解量角器的构造原理是关键。
(4)部分学生不能沟通画角与量角间的联系。
表2 结果表明:42%的学生可以迁移量角的经验来画角,47%的学生由于对量角器认识不彻底而迁移出错。因此,量角的教学着力点需进一步强化对度量核心要素的认识,画角过程中需要打通与量角的联系,找到方法之间的本质联系。

表2 学生画角情况
(二)单元学习目标及结果表现
在单元具体概念的指导下和学生已有经验分析的基础上,本单元的学习目标和学习结果表现具体见表3。在结果表现中,第1 ~7 条对应知能目标,第8 ~9条对应理解目标,第10 ~11 条对应情感目标,第12条对应迁移目标。

表3 单元学习目标及结果表现

表4 “角的度量”单元的具体学习任务及设计意图
三、关键问题及学习任务
基于“角的度量”单元具体概念和学情调研结果,紧紧围绕“发展学生量感”的素养目标,我们形成了本单元学生需要思考的关键问题,设计了本单元的学习任务序列。(如图2)
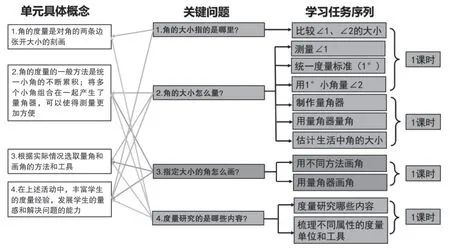
图2
上述的关键问题1 指向具体概念1,4,通过对比两个角的大小,帮助学生明确角的度量是对角的两条边张开大小的刻画。关键问题2 指向具体概念2,3 和4,通过自主探究测量角的大小的方法,获得关于度量单位和度量方法的理解;通过对标准单位的细分,产生统一单位和工具的需求。关键问题3指向具体概念2,3,4,经历用三角尺、量角器等不同工具画角的过程,体会量角器画角的简洁,积累度量的方法和经验。在此基础上,提出关键问题4,引领学生进一步思考度量的核心要素,能迁移这些经验和方法测量其他物体,发展学生的量感。围绕着单元关键问题,形成学习任务序列,共有11 项任务,规划为四个课时,其中最后一课时的任务是在原有课时上增加的。通过这些系统化的学习任务,引领学生逐步增强探究意识,构建度量知识脉络,培养结构化思维。
四、学习任务具体说明
在上述学习任务中,任务1,2 通过比较和初步测量,帮助学生明确度量对象并确定用同属性物体测量角;任务3 给学生提供了丰富的学具,在不断累积单位中产生统一单位的需求;任务5 通过用1°小角来测量角的大小,感受到用单位量角的麻烦以及工具产生的必要性;任务11 引领学生梳理度量相关的知识,除图形与几何领域外,还包括温度、质量、时间等度量,整体思考度量活动的内在一致性,深化对度量本质的理解。
五、单元学习评价
单元学习评价实施不是一个独立的随机事件,而是教—学—评一体的有序实践过程,在实施过程中要贯彻“以评促改”的理念。为评价学生能否迁移研究角的度量的经验和方法,自主研究新的关于度量的问题,我们设计了这样的评估任务(如图3)并制定了相应的评估标准(见表5)。
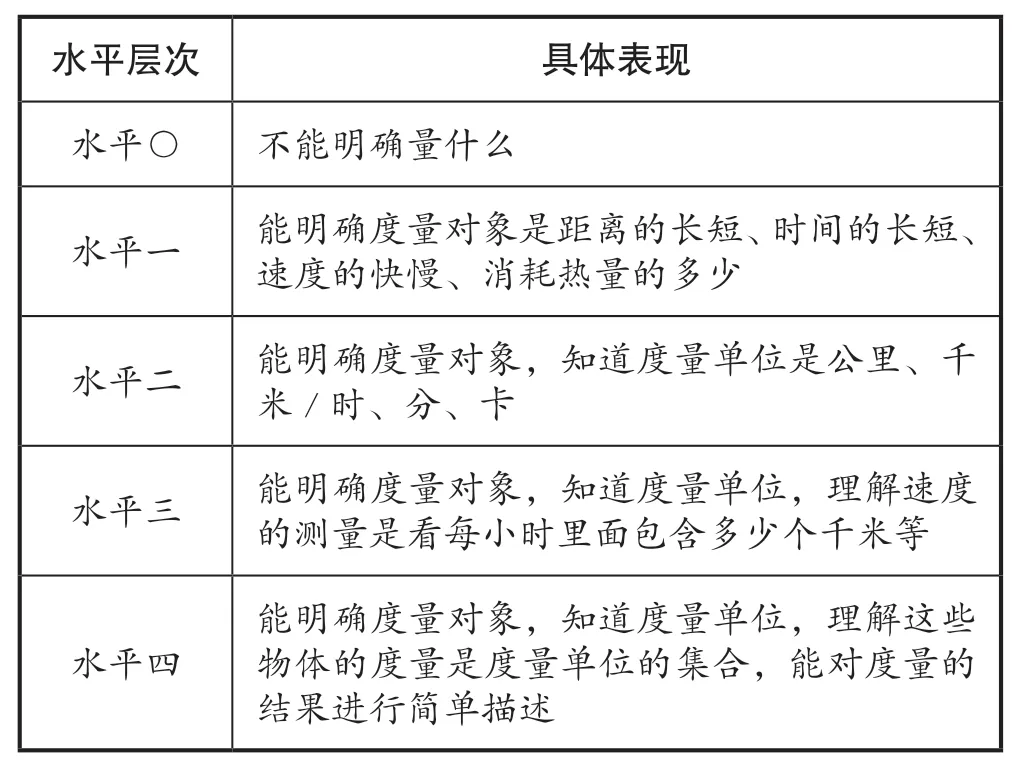
表5 学生自主研究度量的评估标准
六、单元教学反思
基于大概念统领,围绕着“发展学生的量感”的素养目标,本单元的设计从理解度量本质入手,致力于贯通度量学习的一致性,从而实现学习的自主迁移。通过本单元的实践与反思,我们对量感的培养策略有了更深入的认识,主要体现在:
第一,开展以“比较”为中心的数学活动,学生经历从直接比较到间接比较再到运用标准单位比较的过程,充分发展对“数量”的感知;第二,强化“度量单位”的产生与意义,学生结合具体情境识别度量对象的属性,并“创造”或选择合适的度量单位来进行量化;第三,关注度量工具的结构与价值,在建构量角器的过程中理解原理,体会测量的本质;第四,通过“估测”促进对量的感知,创设生活情境给予学生开展估测活动的机会,加强对量的深度体验。此外,本单元的设计因为知识本身的特点,比如度量单位只有1°,不需要借助公式推理转化等,缺乏对量感培养更完整和细致的研究。总之,量感的培养越来越被研究者们重视,其真正落地生根还需要在实践中不断反思和总结。
