基于VMD的圆光栅测角误差补偿方法

张 栋,韦宝琛,2,廖忠骏,岳 义,2

1.上海工程技术大学机械与汽车工程学院;2.上海市大型构件智能制造机器人技术协同创新中心

0 引言

圆光栅作为精密测角元件,在航空航天、智能机器人、高档数控机床、高精度坐标测量仪等领域有广泛的应用[1-3],随着技术的不断发展,对圆光栅编码器测量精度的要求也越来越高。

为进一步提高圆光栅测角精度,国内外学者采用误差补偿方法:多读数头的硬件补偿、基于谐波分析的数值补偿和基于神经网络的软件补偿[4]。苏东风等[5]通过对光栅刻度误差的分析,采用均布四读数头布置方式有效提高了圆光栅测角精度;张文颖等[6]详细推导了多读数头抑制误差的原理,提出了一种采用3个奇读头和4个偶读头相结合的混合布局方式,相比同数量6读数头均匀布置的误差抑制效果更佳,但多读数头的硬件补偿方法使测量系统结构复杂[7],成本提高,且对读数头安装要求较高;李尕丽等[8]针对安装偏心和倾斜产生的系统误差,进行谐波补偿,有效消除了稳定可复现的误差谐波成分,但没有较好地将圆光栅测量系统中的系统误差分离,直接一次性对部分误差进行补偿;洪喜等[9]提出了一种基于径向基神经网络的编码器误差修正技术,实验表明可将标准差从0.82″降至0.24″,很好解决了非线性误差对系统的影响;刘凤伟等[10]针对光电编码器安装、环境等因素提出了一种基于BP神经网络的误差补偿方法,实验结果表明该方法补偿精度高,收敛速度快,显著提高了旋转角度精度。虽然基于神经网络的软件补偿不需要建立误差补偿模型,但其补偿精度依赖数据样本,随机误差对补偿效果的影响较大。真实的圆光栅测角误差是系统误差与随机误差相耦合的[11],圆光栅测角系统的系统误差具有周期性,表现出高幅值低频率特性,然而随机误差表现出没有规律性、不可预见性和高频率特性,随机误差由于其随机性,几乎无法补偿[12]。在误差补偿中,随机误差会影响其补偿模型的精确度,因此,有必要将数据中的系统误差对圆光栅测角误差进行分解和溯源,找到误差的成分,并补偿其系统误差,同时避免过拟合,提高圆光栅测角精度。

为了从圆光栅测角误差中重建系统误差,信号分解是一种有效的解决方法。经验模态分解(EMD)基于Hilbert-Huang变换将信号自适应分解为一系列的模态分量,但EMD具有端点效应和模态混杂,变分模态分解(VMD)基于三维变分约束理论,利用非递归特性估计多个模态分量。F Hu等[13]针对不同温度下,提出了一种经验模态分解和互相关的误差补偿方法,分解不同温度下的误差曲线,利用互相关计算其相关性进行误差分离;N.Cai等[14]提出了一种基于经验模态分解的误差补偿方法,将编码器测量误差分解成若干分量和残差,利用边际谱提取测量误差的趋势。VMD克服了EMD模态混叠和计算量大的缺点,噪声鲁棒性好,具有良好的去噪效果,被广泛应用于非稳态信号分解;Z.Ning等[15]提出了一种基于VMD的误差补偿方法,将光电编码器的误差信号分解成若干模态分量,采用一种从粗选到精选的方法选择合适的模态分量,完成信号重构,但没有对误差进行溯源补偿。

针对圆光栅误差溯源与补偿,本文基于变分模态分解,提出了一种圆光栅测角误差重构和补偿的方法:将原始误差数据分解成若干模态分量,计算其相关因子Ψk,筛选出系统误差成分,再对各模态分量溯源分析得到系统误差的谐波阶次,最后得到误差补偿模型,对圆光栅测角误差进行补偿。实验结果表明:主要成分的谐波阶次识别与常用的谐波补偿方法一致,且加入随机误差后,也能准确识别误差主要成分,该方法降低了随机误差对补偿模型精确度的影响。

1 误差分析

如图1所示,圆光栅测角系统硬件由光栅环和读数头组成。圆光栅测量误差由系统误差和随机误差组成,测量误差Δθ可定义为

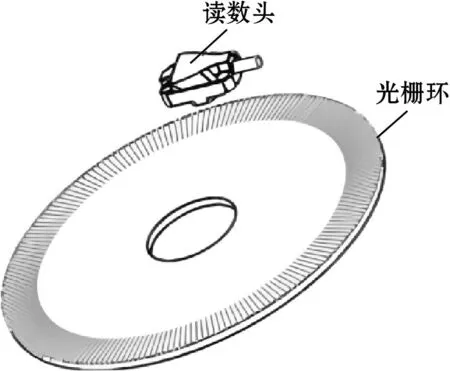
图1 圆光栅编码器结构

(1)

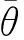
周期性系统误差除了光栅本身制造误差,来自于圆光栅安装偏心产生的一阶谐波误差,通常使用多读数头消除,还包括倾斜所产生的二阶谐波误差,锥面安装也会产生多阶谐波误差。式(1)中es可表示为

(2)

轴系晃动等会产生随机误差,在保证安装精度和采用多读数头测量模式消除部分误差的条件下,随机误差和系统误差的幅值接近,在系统误差得到准确修正后,随机误差的幅值有可能超过系统误差的幅值[16]。

其中随机误差的存在会影响系统误差谐波阶次和幅值大小的识别,为更好地补偿系统误差,需要将系统误差从误差数据中分离出来,以重构系统误差。

2 圆光栅测角误差分解与重构

2.1 变分模态分解(VMD)

VMD将原始误差标定数据X(θ)分解为k个有限带宽的模态函数(intrinsic mode functions,IMFS),表示为

uk(θ)=Ak(θ)cos(ωk(θ))

(3)

式中:uk(θ)为第k个本征模态函数;Ak(θ)为uk(θ)的瞬时幅值;ωk(θ)为uk(θ)的瞬时频率。

模态函数在中心频率ωk处集中,可用高斯平滑偏移信号估算带宽,由于VMD分解的稀疏性,分解时可将其转换成如下问题:

(4)

(5)

式中:δ(θ)为狄拉克函数;*为卷积函数运算符;j为虚数单位。

通过引入增广拉格朗日乘子λ和二次惩罚因子α,将约束变分问题转化为无约束变分问题,得到增广拉格朗日表达式:

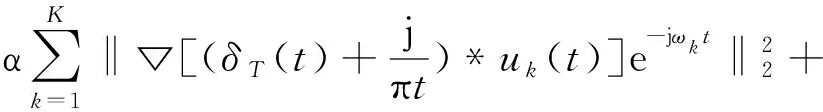
(6)

利用交叉方向乘子法计算靶点即原问题最优解,求解uk、ωk和λ:

更新uk:

(7)

更新ωk:

(8)

更新λ:

(9)

主要迭代求解步骤为:

1)初始化uk、ωk和λ,n=0;

2)确定迭代次数n=n+1;

3)利用式(7)、式(8)、式(9)更新uk、ωk和λ;

2.2 误差重构

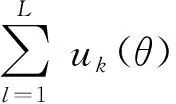
(10)

式中K为IMF的个数;L为测量误差数据点的个数。

与随机误差成分相比,系统误差成分具有典型的低复杂度、高振幅特征。为定量表征各模态分量IMF所含噪声,定义相关因子Ψk:

(11)

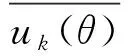
相关因子数值大小可以表示变分模态分解后的模态分量含噪声影响程度,该值越大,表明含系统误差占比越高,噪声影响程度低。

首先将误差数据经过变分模态分解,得到若干个模态分量,计算模态分量的相关因子,剔除含噪声较大的模态分量,重构系统误差。

3 圆光栅误差补偿

由上述误差分析可知,圆光栅系统误差补偿模型F(θ)可表示为

(12)

圆光栅误差补偿方法:首先,对36面棱体标定的误差数据进行变分模态分解,得到若干个模态分量,计算各分量的中心频率,并依次按照从低到高的中心频率值进行排列;其次,基于圆光栅测角误差周期特性,定义一个表征含噪声程度的相关因子Ψ,通过其数值来筛选符合条件的模态分量,将符合条件的模态分量进行重构;通过对分解后的各模态分量溯源,找到原误差数据中的谐波阶次,确定补偿模型中参数i,最后通过仿真软件MATLAB线性回归获得补偿模型中的其他参数,建立误差补偿模型实现误差补偿。通过对比实验详细验证了溯源的可靠性。为验证该方法的抗干扰能力,通过加入高斯噪声的方式,对比补偿效果。误差补偿大致流程如图2所示。

图2 误差补偿流程图

3.1 实验数据获取

针对激光干涉仪测量系统中的圆光栅测量系统,李万红[17]采用自准直仪结合36和23面多棱体对双读数头圆光栅测角系统进行标定实验,采用36面多棱体标定的误差数据平均值建立误差补偿模型,采用23多面棱体标定的误差数据平均值进行补偿效果验证。2组标定数据如图3所示。

图3 文献[17]标定误差数据

3.2 误差补偿实验

36面棱体标定的误差数据通过上述基于VMD的误差重构方法,将原误差数据分解成5个模态分量IMF1～IMF5,设置相关因子阈值ψ=0.6,按照中心频率从小到大排列,如图4所示。

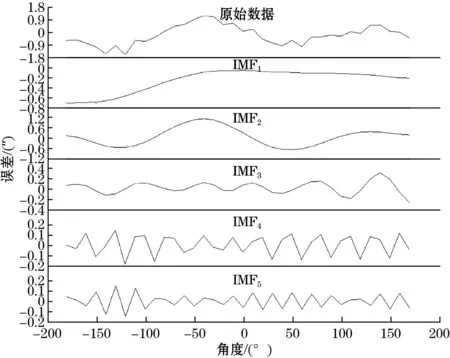
图4 原信号及VMD分解后各模态分量

为判断各模态分量含噪多少,利用式(11)计算5个模态分量的相关因子ψ1～ψ5如表1所示。

表1 模态分量相关因子

其中:

v1(θ)=-0.27+0.1θ+0.2sin(θ+1.78)
v2(θ)=-0.24sin(θ-0.63)-0.66sin(2θ-0.18)
v3(θ)=-0.12sin(6θ-0.05)
v4(θ)=-0.12sin(12θ+1.31)
v5(θ)=0.08sin(16θ+0.16)

由各变分模态分量的相关因子值溯源分析可知:IMF1中包含一阶谐波周期函数和一次线性误差,IMF2中包含一阶、二阶谐波周期误差,IMF3中包含六阶谐波周期函数,但是受一定噪声影响,IMF4包含十二阶谐波周期误差,IMF5含噪声成分较多覆盖周期性特征,且0.08的幅值较小。结合VMD分解后各模态分量的相关因子值和幅值,将F1～F4重构作为系统误差。为了更好补偿360°圆周任意角度的角度测量值,误差数据通过仿真软件MATLAB中的曲线拟合,可以获得误差补偿模型:

F(θ)=-0.284-0.042θ+0.377sin(θ+1.444)-

0.857sin(2θ-0.095)+0.111sin(6θ-

0.293)-0.128sin(12θ+1.294)

(13)

23面多棱体标定误差的平均值为-0.31″、峰峰值为2.33″、标准差为0.68″。基于本文方法的补偿结果表明,平均值、峰峰值和标准差的补偿(补偿百分比)分别降至-0.029″(90.73%)、1.14″(51.07%)、0.29″(57.35%),如图5所示。其补偿效果和补偿后误差趋势与基于谐波方法补偿效果高度相似,表明该方法的准确可靠性。

图5 本文方法与谐波补偿效果图

同时,为进一步验证基于VMD分解对于谐波阶次识别的准确性,在实验中通过增加、减少和代替某谐波阶次进行对比。比较补偿后误差的平均值、峰峰值、标准差,具体补偿效果如表2所示。

表2 补偿效果比较 %

由表2数据可以发现,通过增减或替换某阶次谐波都使峰峰值和标准差的补偿效果有所下降,平均值的补偿量变化较小。也进一步证明基于VMD溯源分析得到的误差的主要成分是准确的。

由上述误差分析可知,随机误差不可忽略,为验证该方法的抗干扰性能,本文通过在误差数据中加入符合高斯分布的随机误差,再分别研究该方法识别误差主要成分的可靠性和补偿效果。

图6 加入随机误差后分解的各模态分量

(14)

式中i=1,2,3,4。

如表3所示,该数值表明在加入标准差为0.1的随机误差时,其各模态分量与原误差信号分解的模态分量相关系数高达96%之上。原误差信号分解的IMF3和IMF4的幅值在0.15左右,当加入方差为0.15和0.2的随机误差时,会导致其模态分量中混杂随机噪声,但相关系数均在77%以上,如图6所示,且周期性特征明显,也能正确识别谐波阶次。

表3 加入随机误差后分解的各IMF相关系数 %

在理想情况下,识别的谐波阶次与不加随机误差一致,假设基于谐波补偿方法能正确识别误差数据的谐波阶次,2种方法的补偿效果如图7所示,为更直观比较2种方法补偿效果,计算2种方法补偿后的平均值、峰峰值和标准差,如表4所示。

表4 补偿效果比较 (″)

图7 加入随机误差后误差补偿效果图

谐波补偿方法只对误差数据进行非线性谐波拟合,在加入随机误差后,谐波补偿方法可能无法识别低幅值的谐波阶次,但基于变分模态分解可以将含噪的误差数据分解成若干有限带宽的模态分量,将含噪程度较大的分量剔除,再根据溯源分析可获得主要谐波成分。实验结果表明,采用该方法补偿效果比基于谐波分析方法的补偿效果更佳。

4 结束语

本文采用VMD将圆光栅误差数据自适应分解,结合表征含噪程度的相关因子Ψ来重构系统误差,能够将数据中稳定的谐波误差部分分离出去。相比谐波补偿方法,基于VMD的误差重构补偿方法不需要多组样本进行反复实验,只需要通过一组误差值就能较为准确得到误差主要成分,而谐波补偿算法则需要通过多组数据建模,分析发现高幅值的系统误差,这要求每组误差数据都准确可靠,谐波分析补偿方法要求误差数据是平稳信号,但在实际测量数据中很难得到保证,本文方法可以处理非平稳信号,可以引入实时补偿方案中,实现对误差数据的重构,适用性更广。