复合梁结构小型六维力传感器的优化设计

孙逸文,陈希良,谢正宇

1.浙江理工大学机械工程学院;2.台州学院智能制造学院

0 引言

六维力传感器能够同时测量空间中某一点的三维正交力分量和三维正交力矩分量[1],用来检测机器人末端操作器接触或抓取工件时所承受的力和力矩,为机器人的力控制和柔顺控制提供力感信息[2],从而完成一些复杂、精细的作业[3]。文献[4]首先提出了Stewart平台在六维力传感器上的应用。Stewart型传感器具有刚度大,理论维间耦合小,无误差累积等优点,但由于其并联结构的特点,有装配误差的存在,导致各分支难以实现力与力矩的各向同性,易造成解耦矩阵病态[5]。文献[6]设计了八竖直梁结构的六维力传感器。竖直梁型传感器具有结构简单、刚度大的优点,但由于刚度的制约,严重影响了传感器灵敏度。E.Bayo等[7]首次提出了一种十字横梁结构六维力传感器,基于十字横梁结构的传感器结构简单、加工成本低,且由于横梁的对称分布,维间耦合不严重,是一种较为理想的结构形式。众多学者对十字梁结构进行衍生设计。李春风等[8]通过在十字梁上打孔使应力集中于孔的两侧,提高传感器的灵敏度。吕志鹏等[9]在十字梁结构上设计浮动梁增大弹性体的应变,并设计了硬件电路使其能无线传输数据。

随着机器人向着轻量化、小型化的发展,需要设计出体型更小、质量更轻的传感器。横梁式六维力传感器主要是通过横梁上的电阻应变片来感知梁上的弯曲应变以实现载荷测量[10],对于十字横梁来说,一般需要粘贴24片电阻应变片才可实现测量目的,由于应变片尺寸限制了十字横梁型传感器向小型化、成本低发展。为此,三横梁(Y)型可进一步解决上述问题,由于采用3个弹性横梁,电阻应变片数量由24片降低至12片,这使得Y型传感器更易实现较小的尺寸,较低成本。

本文在三横梁(Y)型结构的基础上,提出一种新型结构,采用横梁和竖梁复合的形式,兼顾了横向和竖向的应变效果,为了便捷地嵌入机械臂的主要部位,设计出一款外径40 mm的六维力传感器弹性体结构。三横梁(Y)型结构弹性体的应变片贴在应变梁的四周,应变片尺寸的大小会限制应变梁的高度和宽度,小型化限制弹性体的大小,即限制了应变梁的长度,导致应变梁的长宽高均受限制,优化困难。本文设计的复合梁结构弹性体的应变片贴在横梁的上下两面和竖梁的左右两面,仅限值了应变梁的宽度,且竖梁的长度不影响弹性体的外径,具有良好的优化空间,使其小型化的基础上,保证较好的测量精度。

1 弹性体结构设计及有限元分析

1.1 弹性体结构

多维力传感器设计的难点与核心是传感器弹性体的结构设计,弹性体的结构设计直接影响传感器的灵敏度、线性度、重复性等指标[11]。本文设计了一种三横梁、三竖梁复合式结构的六维力传感器,如图1所示。弹性体结构如图2所示,包括外法兰(上)、中心平台、外法兰(下)和6个应变梁。其中3个横梁彼此成120°角,连接外法兰(上)与中心平台,3个竖梁同样成120°分布,连接上下外法兰。外法兰直径为D,中心平台直径为d,横梁宽度为W1,高度为H1,竖梁长度为L2,宽度为W2,高度为H2。

图1 六维力传感器爆炸视图

图2 复合梁弹性体结构

1.2 铁木辛柯梁力学模型

若要实现六维力传感器的小型化,必然要减小应变梁的长度,因此需要用铁木辛柯梁来建立力学模型[10],欧拉-伯努利经典梁理论则不适用。如图3所示,欧拉-伯努利梁理论认为剪切刚度无限大,不发生剪应变,从应用上看,跨高比大于5的梁通常是弯曲主控的,用欧拉梁即可模拟,跨高比小于5的梁,剪切变形明显,铁木辛柯梁则更为合适。由于铁木辛柯梁理论计入了剪切变形和转动惯量的影响,在描述传感器弹性梁的行为上比欧拉-伯努利梁更为精确。

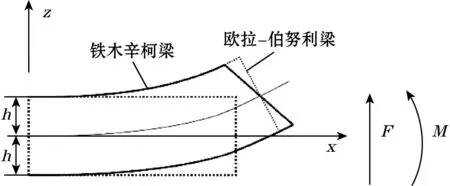
图3 铁木辛柯梁和欧拉-伯努利梁对比

当力/力矩作用于弹性梁上时,弹性梁发生弯曲变形,弹性梁的应变可用梁上某一点的挠度ω和转角φ表示,变形梁的内力,即剪力和弯矩,与挠度和转角的关系如式 (2)所示。铁木辛柯梁及其微段如图3所示。

(1)

式中:F为剪力;M为弯矩;A为横截面面积;I为截面关于中性轴的惯性矩;E、G、K分别表示杨氏模量、剪切模量和剪切系数,矩形截面一般取K=1.2。

建立平衡方程:

(2)

式(1)和式(2)是铁木辛柯梁理论的2个基本公式。当给定足够的边界条件时,可以计算得到挠度ω(x)和转角φ(x)的解析解。弹性梁上任意一点的应变值可以由式(3)计算得到:

(3)

式中z为梁上任意一点到梁的中性层的距离。

由于应变片只能贴在弹性梁的表面,因此z=h/2,h为应变梁的高度,因此有:

(4)

1.3 弹性体有限元分析

通过借助Ansys Workbench对初始六维力传感器的弹性体进行有限元分析,得到各工况载荷(Fx、Fy、Fz、Mx、My、Mz)下的应变敏感区。六维力传感器的测量范围和初始尺寸参数如表1所示,弹性体材料为2024-T6,材料参数如表2所示。

表1 六维力传感器的量程和初始参数

表2 弹性体材料参数

将建立的三维模型导入ANSYS Workbench,其中固定约束应用于下外法兰底部,6种载荷工况施加于中心平台的上表面,Fx=50 N;Fy=50 N;Fz=50 N;Mx=2 N·m;My=2 N·m;Mz=2 N·m。

如图4所示,在Fx=50 N的条件下,3根竖梁发生弯曲变形,最大应变位置出现在竖梁靠近下端外法兰处;在Fy=50 N的条件下,与弹性体受Fx时类似;在Fz=50 N的条件下,3根横梁的上、下表面有较大的应变,最大应变位置出现在横梁和中心平台的连接处。在Mx=2 N· m的条件下,横梁AB受扭,横梁CD、EF弯曲,最大应变位置出现在横梁和中心平台的连接处;在My=2 N· m的条件下,3根横梁均发生弯曲变形,最大应变位置出现在竖梁靠近下外法兰处;在Mz=2 N· m的条件下,3根竖梁发生弯曲变形,最大应变位置出现在竖梁靠近下外法兰处。

图4 弹性体的应变分布

2 应变片布置及组桥

弹性体的有限元静态分析结果表明,弹性体受Fx、Fy和Mz时,引起三竖梁的两侧面弯曲变形,受Fz、Mx和My时,引起三横梁的上下面弯曲变形。应变梁受到弯曲变形时,一侧受拉,另一侧受压,受拉的一侧应变值为正,受压的一侧应变值为负。因此,根据这个特性,在6个应变梁上粘贴12片应变片组装6个半桥电路如图5、图6所示。

图5 应变片的粘贴方案

图6 惠斯登电桥方案

当弹性体受到Fx正方向的力时,5号、6号弹性梁发生弯曲变形,应变片S9和S12的电阻值增大,S10和S11的电阻值减小。由于ΔR远小于R,因此ΔR的高次项可忽略不计。半桥电路的输出如下:

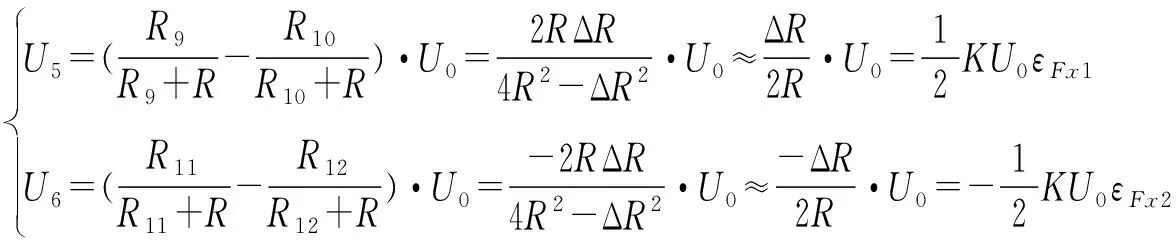
(5)

U1～U6为6个半桥的输出电压,U0为惠斯登电桥的供电电压,ΔR为应变计电阻的变化值,εFx～εMz分别表征在Fx～Mz各载荷分量下的应变片工作区域的平均应变量。类似的,推导出在单轴负载条件下,6个半桥式电路的信号输出如表3所示。

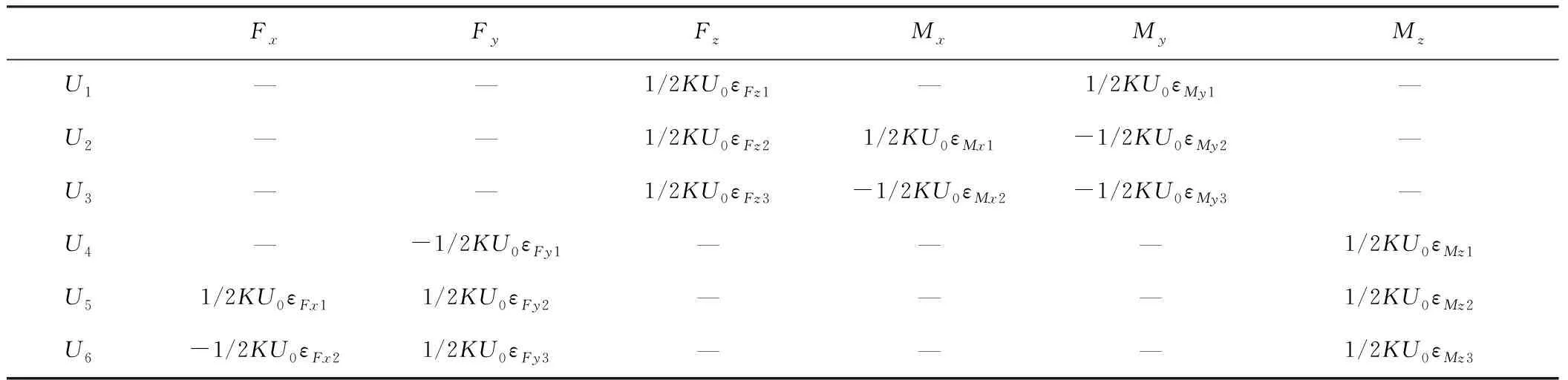
表3 单轴荷载下电桥的输出信号分布

3 基于响应面法的弹性体参数优化

3.1 实验设计

响应面分析法(RSM)是通过近似构建具有明确解析表达式的多项式来描述系统的输出响应与系统的输入变量之间关系的方法。该方法可用于预测弹性体在不同结构参数下的输出响应,如最大等效应力、应变、质量等,从而实现弹性体的优化设计[12]。由RSM建立的数学模型如下:

yi=fi(x1,x2,…,xn)+e

(6)

式中:yi为因变量目标响应值;x1,x2,…,xn为自变量影响因子参数;fi为响应面函数;e为误差。

考虑试验设计的经济性,结构优化分析的高效率和适用性,采用响应面模块中拟合精度较高的Box-Behnken design(BBD)试验设计方法,并用Kriging空间插值法进行修正以增加响应面模型的精度。根据不同设计变量的范围选取合适的试验样本点,使用Ansys Workbench对各组方案计算应力应变结果。

为了考虑六维力传感器的使用寿命和灵敏度,约束设置如下:单轴满载条件下的最大等效应力不大于材料的疲劳极限,六维力满载条件下的最大等效应力不大于材料的拉伸屈服强度,如式(7)所示,材料属性如表2所示。

(7)

根据Workbench计算结果,当弹性体分别受Fx、Fy、Fz和Mz时,最大等效应力远小于材料的疲劳极限140 MPa,因此只需要考虑弹性体受Mx、My和六维力满载下的最大等效应力情况即可。

3.2 构建优化方程及响应面数学模型

当弹性体受到Fx正方向的力作用时,由于5号、6号弹性梁呈x轴对称分布,故梁上工作区域弹性应变均相同,可得Fx目标优化方程f1为

maxf1=2(εFx9+εFx10)

(8)

当加载Fy正方向作用力时,4号、5号和6号3个弹性梁均存在弯曲应变,此时目标优化方程f2为

maxf2=εFy7+εFy8+εFy9+εFy10+εFy11+εFy12

(9)

当弹性体受到Fz正方向的力作用时,由于1号、2号、3号弹性梁沿圆周方向呈120°对称分布,故各个梁上的工作区域弹性应变均一致,可得Fz目标优化方程f3为

maxf3=3(εFz1+εFz2)

(10)

与受Fx正方向的力作用类似,弹性体受Mx正方向的力矩时,2号、 3号弹性梁呈x轴对称分布,故梁上工作区域弹性应变均相同,可得Mx目标优化方程f4为

maxf4=2(εMx3+εMx4)

(11)

与受Fy正方向的力作用类似,弹性体受My正方向的力矩时,1号、2号、3号横梁均存在弯曲应变,可得My目标优化方程f5为

maxf5=εMy1+εMy2+εMy3+εMy4+εMy5+εMy6

(12)

与受Fz正方向的力作用类似,弹性体受Mz正方向的力矩时,由于4号、5号、6号竖梁沿圆周方向呈120°对称分布,故各个梁上的工作区域弹性应变均一致,可得Mz目标优化方程f6为

maxf6=3(εMz7+εMz8)

(13)

应力约束如下:

(14)

根据铁木辛柯梁应变式(5)及敏感性分析进行参数筛选,剔除了对弹性体的应力和应变影响不大的可变因素。同时,考虑到六维力传感器形状尺寸的限制,选择主要影响变量为中心平台半径、应变横梁高度、应变竖梁高度和应变竖梁长度,将其作为自变量结构参数x1、x2、x3、x4输入至参数集中。同时,将上述多目标优化方程目标响应值f1～f9作为参数集的输出参数。计算得到25组分组数据并导入Minitab软件中,得到多目标优化方程响应面模型为式(15),方差分析如表4所示。

表4 响应面模型误差分析

(15)

由表4可知,各响应面模型P值均小于0.01,表明各回归方程统计意义极为显著,且方差均大于99%,调整方差均大于97%,说明响应面模型具有较高的可信度与准确性。

3.3 基于多目标遗传算法的结构优化

多目标遗传算法(multi-objective genetic algorithm,MOGA)是一种模拟自然进化的建模方法,被广泛应用于解决复杂的优化问题,特别是多目标优化问题[12]。此算法类似于遗传算法,它利用遗传演化算法和对抗性进化算法来搜索和优化不同的目标。MOGA 借鉴了生物学中心脏进化理论,以及模拟自然进化的思想,并用于解决复杂的多目标优化问题。

根据3.2节的优化方程和结构尺寸的限制,建立弹性体结构的优化数学模型如下:

FindX={x1,x2,x3,x4}

使用MOGA进行优化,设定初始样本为4 000,每次迭代的样本数为800,最大迭代次数为20。经过10次迭代后收敛,评价次数为10 596次,生成样本集的大小为800,产生1个候选点。将结构参数优化后的弹性体有限元模型进行求解,优化后各参数的计算结果与初始结果如表5所示。

表5 弹性体优化前后参数对比

由表5可知,传感器优化后结构参数C-1对照组中灵敏度性能指标f1～f6高于初始结构参数C-2,分别是优化前的1.583 3、1.563 2、1.733 8、1.511 3、1.510 9、2.171倍,验证了响应面法与MOGA寻优算法的可靠性。为了容易加工制造,圆整至易加工的值,x1=7 mm,x2=2.9 mm,x3=2 mm,x4=9 mm,实物如图7所示。

图7 六维力传感器实物图

4 标定实验及解耦

本文中根据上述分析试制了铝合金的六维力传感器弹性体,并对该六维力传感器进行贴片、组桥和静态标定。标定平台如图8所示,将力传感器固定在工装夹具上,通过砖码悬垂的重力完成各个方向的标定。其中夹具A标定Fx、Fy和Mz,夹具B标定Mx、My和Fz,图9为夹具A标定Fx和夹具B标定Fz。由于加载盘有厚度,标定时需要计算产生的附加力和力矩,否则会影响解耦精度。

图8 标定实验系统

图9 六维力传感器的标定

实验时依次对六维力传感器的Fx、Fy、Fz、Mx、My、Mz,加载至满量程力值,每次加载砝码质量为1 kg,从0值加载至5 kg,获得加载力矩阵F。矩阵F中各列为每次加载的力或力矩,其中产生的附加力和力矩也一并算入其中。同时采集传感器6条输出通道的电压,待加载稳定后,每隔20 s取一次值,共取3次并计算平均值,得到输出电压矩阵ΔU,绘制六维力传感器静态标定曲线(图10)。

(a)Fx静态标定曲线

图10表明:由于Y型结构没有中心对称面,无法利用结构的对称性抵消耦合,因此各个方向的耦合较为严重,需要进行解耦运算。输出电压与标定载荷的关系有较好的线性度,可以使用最小二乘法进行线性解耦。根据式(16),计算出解耦矩阵G。

G=F*ΔUT(ΔU*ΔUT)-1

(16)

通常采用Ⅰ类误差和Ⅱ类误差作为传感器解耦精度指标。如式(17)所示,A、B为传感器六维力中的任一方向力。

(17)

对传感器各方向施加满量程的力,获得满量程加载力矩阵F1,同时提取各通道输出信号,获得矩阵ΔU1,根据式(16)计算检测力矩阵F2,根据式(17)对比F1和F2,从而计算出误差矩阵E。

误差矩阵E主对角线的元素即是该传感器的I类误差,其余位置为Ⅱ类误差。该传感器的Ⅰ类误差最大值为0.596%,Ⅱ类误差最大值为1.665%。Ⅰ类误差均在1%以内,II类误差均在2%以内,表明误差较小,传感器解耦精度较高。

5 结论

本文设计了一种铝合金的六维力传感器,设计了一种复合梁结构的弹性体结构,并通过Box-Behnken响应面法优化了应变片贴片位置的平均应变,根据仿真结果,6个方向上的应变分别是优化前的1.583 3、1.563 2、1.733 8、1.511 3、1.510 9、2.171倍。制作样机进行了静态标定实验,通过最小二乘法的线性静态解耦,计算结果显示所设计的六维力传感器的Ⅰ类误差分别为:0.18%、0.42%、0.41%、0.05%、0.49%、0.6%,Ⅰ类误差最大值为0.49%,Ⅱ类误差最大值为1.665%。综上所述,采用复合梁弹性体结构可以使传感器易小型化的同时,进一步保证合理的测量精度。