基于IMU在线校准的SLAM精度提升方法研究

周霆威,乔贵方,刘 娣,付冬梅,张 颖

南京工程学院自动化学院

0 引言

随着机器人技术的发展,移动机器人可代替或协助人类完成各种困难工作[1]。SLAM技术[2]是移动机器人实现精确建图,并进行路径规划的核心技术之一[3]。目前SLAM算法主要分为基于激光雷达的SLAM算法与基于视觉相机的SLAM算法。但基于单一传感器的SLAM算法在建图和导航精度方面具有一定的局限性。随着传感器技术的发展,通过多传感器的数据融合能够实现高精度的SLAM算法。基于多传感器融合的SLAM算法主要有视觉与惯性测量单元(inertial measurement units,IMU)的融合SLAM[4]、激光雷达与IMU融合SLAM[5]以及激光雷达、视觉和IMU融合SLAM[6]等。以上算法中IMU提供精确的位姿估计,但IMU存在的系统误差与随机误差决定了其位姿估计精度,进而影响SLAM技术的建图精度。因此,在使用前需要对IMU进行精确标定,标定过程中会采用精密转台等相关设备进行IMU的误差测量。文献[7]中采用了多位置法对加速度计的零偏和尺度参数进行校准,但该校准过程需要在单轴转台上进行。文献[8]中利用三轴惯导测试转台进行了IMU六位置静态分立式标定,有效地提高了IMU的测量精度。但是上述标定方法均是利用外部精密设备对IMU进行标定,同时标定过程较为复杂。文献[9]通过手动调整IMU的位姿来对其系统误差进行离线标定,无需采用外部测量设备,但不适用于移动机器人平台的自动化运行。而IMU的系统误差和随机误差会随时间推移而发生变化,离线标定无法满足后期的精度要求。因此,本文提出了一种易于实现的在线校准方法,用于解决IMU长期使用过程中的误差问题。首先建立了IMU中加速度计与陀螺仪的误差模型;其次设计了IMU的在线两步标定方法,实现误差模型的参数辨识;最后通过实验验证本文提出的在线两步标定方法,并基于搭建的移动机器人平台验证IMU在线标定对SLAM建图精度的影响。

1 误差模型的分析与构建

理想情况下,IMU中加速度计与陀螺仪为同一参考正交坐标系,但在制造过程中会引入不同的误差源,如非正交误差、比例因数误差和零位误差。本文将加速度计与陀螺仪的误差模型表示为:

aI=TaKa(aS+ba+na)

(1)

ωI=TgKg(ωS+bg+ng)

(2)

式中:aI、aS分别为加速度计的实际值和测量值;ωI、ωS分别为陀螺仪的实际值和测量值;Ta、Tg分别为加速度计与陀螺仪的非正交误差的坐标轴偏移矩阵;Ka、Kg分别为加速度计与陀螺仪的比例因数误差的缩放矩阵;ba、bg和na、ng分别为加速度计与陀螺仪的零位误差和噪声。

非正交误差如图1所示,因此,非正交坐标系与正交坐标系之间的转换矩阵为

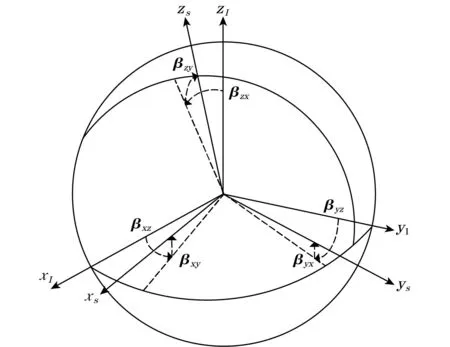
图1 IMU内部传感器理想坐标系(xI,yI,zI)与实际坐标系(xS,yS,zS)

(3)

式中βij表示加速度计或陀螺仪在实际坐标系i轴绕着理想坐标系j轴的旋转。

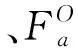
(4)

式中利用αij来代替一般情况下的βij,表示加速度计旋转的角度量。

陀螺仪的测量与加速度计参考相同坐标系,则Fg与FI之间的转换矩阵为

(5)

式中利用γij来代替一般情况下的βij,表示陀螺仪的旋转角度量。

误差模型中比例因数误差矩阵Ka与Kg的定义分别为:

(6)

(7)

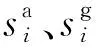
加速度计和陀螺仪的零位误差ba与bg定义分别为:

(8)

(9)

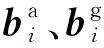
2 IMU标定方法

IMU标定主要分为2步:首先辨识加速度计的误差参数,然后基于加速度计的标定结果实施陀螺仪传感器的误差参数辨识。

2.1 加速度计标定方法

基于上述的IMU误差模型,加速度计待辨识的误差参数向量θacc如下:

(10)

在标定过程中,本文利用滑动窗口对窗口内的数据进行均值计算,可忽略噪声值的影响,将误差模型修改为

aI=h(aS,θacc)=TaKa(aS+ba)

(11)

加速度计标定数据测量过程如下:

1)将IMU静置Tinit=50 s,并计算Tinit时间的测量方差ζinit;

2)调整IMU姿态,并保持静止twait=3 s;

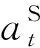
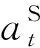
5)重复步骤2)～步骤4),采集N=40段数据;

6)利用L-M算法求解θacc。

当IMU处于静止时,加速度计向量的模长与重力加速度值相等。因此,通过多次改变IMU的姿态,可根据重力加速度的测量值与实际值构建代价函数:

(12)

式中‖g‖为该地重力矢量的实际大小。

2.2 陀螺仪标定方法

本文利用Allan方差对陀螺仪的零位误差进行标定[10],其中零位误差一般取Allan方差曲线底部平坦区域的最小值,噪声误差同样进行忽略。其余误差参数采用非线性优化方法进行辨识,构造陀螺仪误差参数向量θgyro如下:

(13)

陀螺仪标定数据的测量过程如下:

1)将2段静态数据中的加速度计方向向量均值作为初始值和终值;

2)旋转过程中,对陀螺仪输出数据进行积分,计算得到两端静态数据之间的旋转矩阵;

3)利用加速度计方向向量初始值和旋转矩阵计算加速度计方向向量终值的预测值;

4)重复步骤1)～步骤3),采集N=40段数据;

5)使用L-M算法辨识θgyro。

陀螺仪的数据测量是以标定后的加速度计输出值为参考真值。通过多次改变IMU的姿态,可根据加速度计输出值和陀螺仪旋转矩阵,定义如下代价函数:

(14)

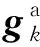
3 实验验证及结果分析

3.1 移动机器人平台搭建

本文采用的移动机器人为两轮差分结构,移动机器人上安装主控单元Raspberry Pi 4B、二维激光雷达RPLIDAR A2、二轴舵机云台和IMU模块BWT901CL。二维激光雷达RPLIDAR A2的测量半径为0.2～12 m,角度分辨率为0.45°,扫描频率为10 Hz。IMU模块BWT901CL的采样频率为0.2～200 Hz。二轴舵机云台的控制分辨率为0.088°。以上器件的安装如图2所示。

图2 移动机器人平台搭建

IMU模块BWT901CL安装在轴舵机云台上,X轴正向为移动机器人的前行方向,X-Y平面与移动机器人上平面平行。

3.2 IMU的误差参数辨识

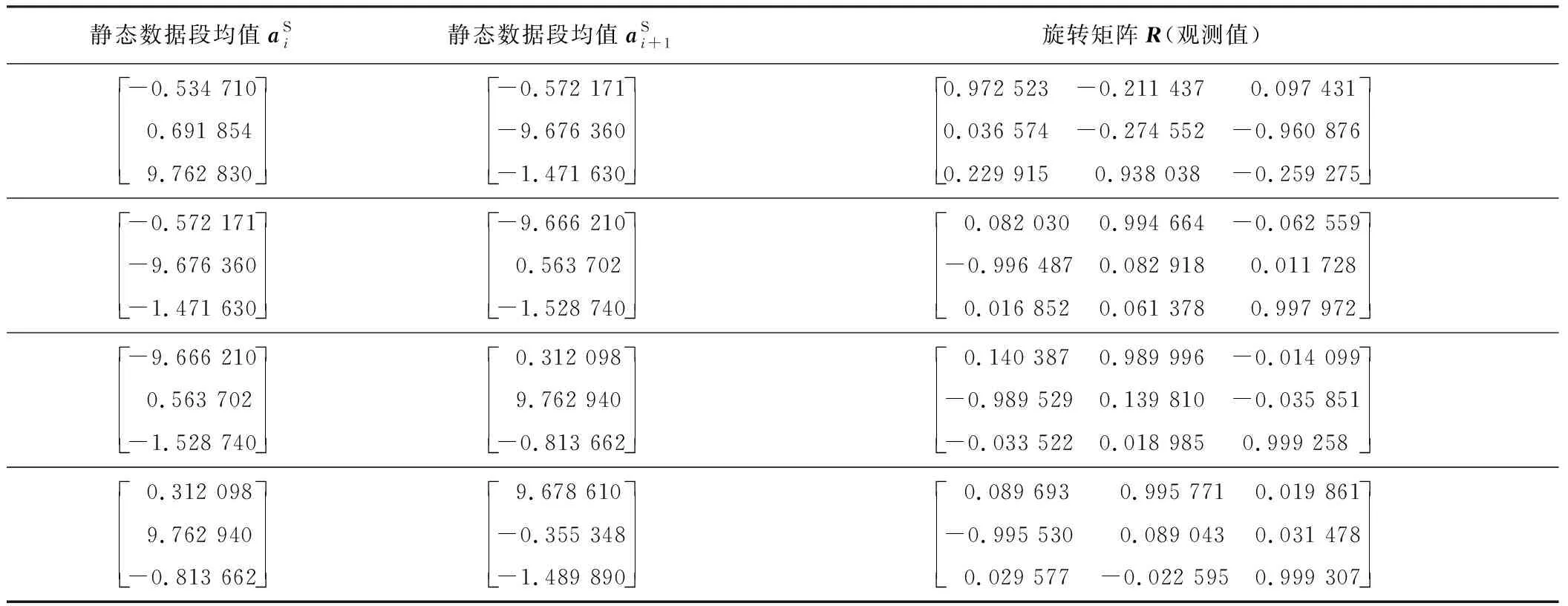
表1 标定校准过程数据处理(部分)

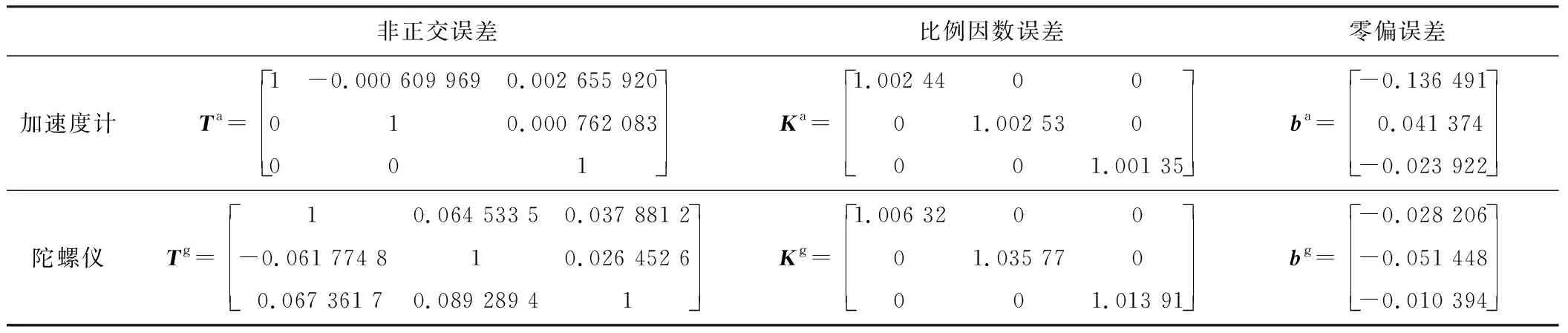
表2 IMU标定后的参数误差

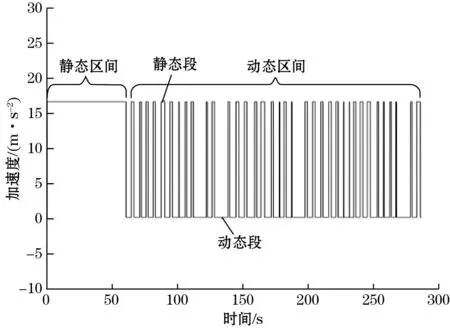
图3 静态检测器检测结果

3.3 SLAM地图构建精度对比

为验证IMU标定结果对于SLAM建图精度的影响,本文基于以上移动机器人构建的实验场景如图5所示,该实验为8 m×8 m正方形场地。

图5 SLAM建图实验环境搭建

为了更好地对比建图精度,控制移动机器人从A点依次按照图5中的逆时针和顺时针在实验场景中移动,并记录相关传感器的数据,构建移动机器人SLAM数据包。本文采用Cartographer算法进行地图构建[11],并在算法中将IMU数据、二维激光雷达的点云数据与里程计数据进行融合,算法流程如图6所示,在该算法中IMU的输出数据需要通过在线校准后再与其他传感器进行数据融合。

图6 基于Cartographer的融合建图结构框图

在对比实验中,分别采用原始的IMU输出数据和校正后IMU输出数据进行SLAM建图,通过Cartographer算法获得的最终地图如图7所示。从图7(a)中可以看出,用未标定的IMU构建的地图在四边都存在一定的错位畸变现象,同时变现也较为模糊。而从图7(b)中可以看出,用标定后的IMU构建的地图边界较为平整、清晰,建图效果相对图7(a)更好,因此,可以得到经过标定的IMU能够有效地提高移动机器人的建图精度。

(a)标定前

4 结论

本文针对移动机器人的SLAM建图精度展开研究,提出了一种易于实现的IMU在线标定方法。该方法不依赖外部测量设备,仅需移动机器人通过二维舵机云台进行多个姿态调节,即可实现IMU中加速度计和陀螺仪误差模型参数的精确辨识,较大程度地提高了IMU的标定效率。最后为了验证本文提出的IMU在线标定方法对于SLAM建图精度的提升效果,基于搭建的移动机器人硬件平台和Cartographer算法分别对标定前和标定后的二维地图精度进行对比,结果表明,经过标定后的IMU能够有效地提升建图精度,从而也说明了本文提出的IMU在线标定算法具有较好的标定精度。