基于RSM和GWO-BP混合代理模型的三维车削力传感器开孔位置多目标优化设计

韩继科,王 鹏,2,张昌明,2,戴裕强

1.陕西理工大学机械工程学院;2.陕西省工业自动化重点实验室

0 引言

多目标优化设计适用于机械结构参数优化[1]、结构分布数量优化[2]等方面,针对不同的结构选用不同的拟合模型,寻找最优的结构形状对应的最佳工作性能。文献[3]提出了一种机床支撑部件内部加强筋布局的新方法,确定了遗传算法和BP神经网络(GABPNN)方法在元模型精度方面的优异表现,并通过仿真和实验验证了该方法的有效性。文献[4]用径向基神经网络(RBF)对永磁同步电机的参数和性能之间进行拟合,利用MIGA算法电机进行结构参数优化,经有限元验证,其转矩脉动减小了84%,结果误差为4.9%。文献[5]为了获得最佳的永磁电机散热性能,研究了13种代理模型的拟合精度,从中选择拟合优度最好的BP神经网络作为代理模型,使用6种优化算法进行优化,选择误差最小的GDE3算法,优化后的冷却液压力得到明显提高。文献[6]提出了一种基于RBF神经网络和NSGA-II优化算法的环形泵多目标优化方法,以吸入角、扩散角、面积比和流量计作为设计变量,以射流泵效率和水头比为优化目标进行多目标优化,射流泵扬程提高了30.46%。文献[7]借助BP神经网络对C919变压整流器单元的陷波滤波器参数和传导发射抑制效果之间进行非线性拟合,使用改进的NSGA-II(简称γ-NSGA-II)对陷波滤波器的重量和成本进行了多目标优化,经过试验测试,陷波滤波器传导干扰满足要求。文献[8]通过高斯回归来建立并联机械手的设计变量和目标函数之间的映射关系,使用粒子群算法对高斯回归代理模型进行优化,机械手性能指标明显提升。上文提到的拟合模型均采用单一的BP或者RBF进行拟合,其拟合模型未进行有效优化,拟合精度不高。

文献[9]开发了一种改进粒子群算法(PSO)算法优化的径向基神经网络(RBFNN)代理模型,建立了多参数天线结构快速多目标优化的框架,降低了依赖高保真电磁仿真的传统天线设计方法的设计成本。文献[10]开发了一种预测和优化切削力、刀具磨损、震动、表面质量和功耗的混合算法,使用反向神经网络进行拟合,采用多目标粒子群算法进行优化,表面质量和刀具寿命的预测准确性得到提高,功耗降低。文献[11]提出一种基于受限玻尔兹曼机和反向传播神经网络的代理模型对冲压过程中的工艺参数和成型质量之间进行拟合,使用基于拥挤算子的多目标粒子群算法对代理模型进行多目标优化,结果表明在不过度减薄的情况下减小了凸缘皱纹,提高了成型零件的均匀性。文献[12]使用改进的PSO-BP神经网络对翼型翅片印制电路换热器的布置参数和优化目标(努塞尔数和范宁摩擦因数)进行拟合,用NSGA-II对代理模型进行多目标优化,将基于TOPSIS方法的方案确定为最佳选择。以上模型均是在单一拟合模型基础上进行优化,模型精度进一步提升。

本文开发出一种混合GWO-BP和二次多项式的代理模型,使用12种优化算法对混合代理模型的高维Pareto前沿面进行筛选,又横向对比不同算法的IGD和HV指标,得到SparseEA算法在混合代理模型上拥有较好的性能。优化后的传感器变形量和等效应力均有不同程度的提升。

1 十角环开孔位置规律分析

1.1 十角环传感器简介

传感器弹性体由2个正交十角环组成,为了获得车削加工过程中的三向力(主切削力、进给力、吃刀抗力),本文采用车刀刀柄即是传感器的设计理念,设计出一款一体化车削力传感器,十角环首端是一个全对中式刀头,数控刀片安装在刀头卡槽处。传感器结构如图1所示。

图1 传感器结构

将传感器结构装夹在车床上,切削加工时切削力传递到十角环上,十角环上的电阻应变片通过全桥电路将应力转化为电压变化,通过线缆连接后端放大和滤波电路得到信号,从而实现切削力的测量。根据实验测得其三向灵敏度为:在5 V供桥电压下,Fc为11.6 mV/N,Ff为10.44 mV/N,Fp为1.8 mV/N。可见其Fp方向灵敏度明显小于其余两者。

1.2 开孔位置

为了进一步提升十角环的灵敏度,现针对十角环进行开槽,在应变片位置下,在十角环环臂开通孔,开孔位置如图2所示,由A、B、C、D、E决定。其中A、C、E为开孔到桥臂边缘的距离,B、D分别为前侧开孔直径和后侧开孔直径,A+B+E为固定值。

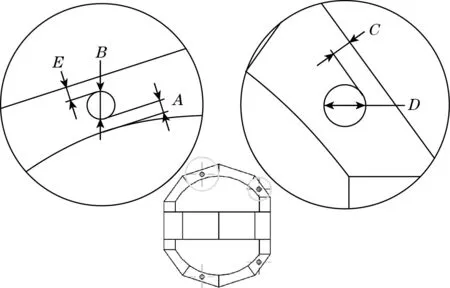
图2 开孔位置

1.3 孔边应力规律

采用有限元软件进行应力分析,刀头位置施加三向力各为200 N,刀柄约束固定。图3(a)为有限元网格图,采用六面体主导,最小单元质量为0.6,其中网格数为337 453,节点数1 194 013,单位质量为0.87,材料选用17-4PH,弹性模量为205 GPa,泊松比0.29,密度为7 790 kg·m-3。

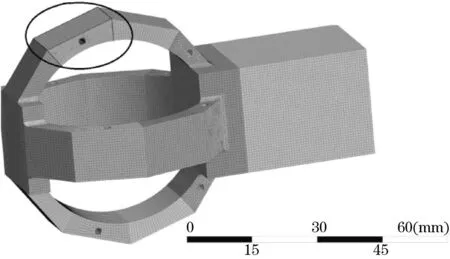
(a)传感器有限元网格图

为研究开孔位置和开孔大小对结构的影响,设置2个评价指标[13]:

第1个评价指标为路径应力的最大值。图3(b)为截取的其中一段桥臂,取图3(b)中1至2,得到路径应力的变化规律如图3(c)所示,可以看到应力最大出现在路径中间位置,此位置为粘贴应变片位置,此评价指标反映左侧孔对传感器灵敏度的提升情况,指标越大,传感器灵敏度越大。

第2个评价指标为整体结构的等效应力,本指标反映传感器承受的应力极限,应该控制在300 MPa以下,维持在材料屈服强度以内。

分析在不同孔径和不同孔距下2个评价指标的变化情况,得到图4(a)、图4(b)。对于路径应力图4(a),在孔距一定的情况下,开孔越大,路径最大应力越大。在孔径一定的情况下,随着孔距的增加,路径应力会先下降后上升,应力上升的情况说明在靠近刀头的4个通孔的孔距应该尽量大,因为靠近刀头的通孔位置的上下都贴有应变片,孔距越大,路径最大等效应力上升,靠近通孔的应变片位置处应力也会变大。

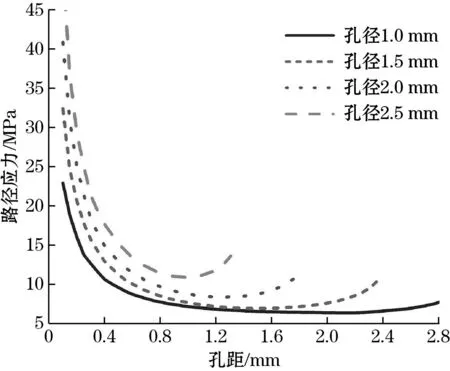
(a)路径应力变化图

由图4(b)可以看出,随着孔距的增加,最大等效应力先减小后增大,随着孔距越来越大,最大应力会出现位置转移的现象,原本结构等效应力为十角环和刀柄的交界处,开孔之后,最大等效应力出现在靠近刀柄的孔边缘处,说明孔的位置是可以改变十角环应力结构。得出结论:左侧周向布置的孔距应该靠近圆环。右侧周向布置的孔距应远离圆环。

2 混合代理模型构建

2.1 高维空间采样方法

设计变量为图2所示,左侧孔径P2(B),左侧孔边距P3(C),右侧孔径P1(A)和右侧孔边距P4(D)。3个优化目标为传感器整体平均变形量,传感器结构一阶固有频率和第一评价指标,前2个优化目标分别对应传感器的灵敏度和刚度,2个目标相互约束,设计变量的取值范围如式(1)所示。

(1)

本文选用拉丁超立方(LHS)和最佳空间填充技术(OSF)进行采样。最佳空间填充原则为:最大最小距离准则,最大最小距离表示将空间分布点的最小距离最大化,避免空间分布点出现局部采样密集现象,表达式为

(2)

式中:M为2个点最小距离的最大值;n为采样点数目;d(xi,xj)为2个点的距离。

d(xi,xj)表达式如下:

(3)

式中:q为因素个数;m=1为矩形距离,m=2为欧几里得距离。

为度量采样点在实验区域中散布的均匀程度,这里引入评价指标CL2(中心化L2偏差),其可以定义为

(4)

CL2越大代表样本在空间分布越均匀。CL2不仅可以评价空间点的均匀程度,还可以评价空间点投影到各个平面的子空间的均匀性。文献[14]通过最小化设计的中心化L2偏差准则定义了均匀设计。

图5为2种采样方法对应的CL2偏差,随着采样点数目增加,偏差逐渐减小,但是逐渐趋于平缓,取采样点数目N=100制作图6的空间分布点,图6(a)～图6(c)为LHS采样,其CL2=0.044。图6(d)～图6(f)为OSF采样,其CL2=0.028。说明OSF采样的空间分布均匀性要优于LHS。图6的XY坐标对应的是设计变量,Z轴对应的是优化目标。从图6也可以看出OSF采样的效果要优于LHS采样。

图5 不同采样点偏差规律

2.2 响应面模型

响应面(RSM)模型基于最小二乘法原理,将100组实验数据得到的估计值拟合到二次多项式模型中,二次多项式一般形式为

(5)

Pk为响应项(k=5为平均变形量,k=6为固有频率,k=7为等效应力);β0、βi、βj、βij为常数项、平方项、交互项、单项的回归系数;Xi、Xj为设计变量。

表1是关于P5(平均变形量)、P6(固有频率)、P7(等效应力)的P值,当P值大于0.05,说明影响不显著,将其删除。删除后得到P5、P6、P7和P1、P2、P3、P4的二次多项式。

表1 多项式对应的P值

(6)

(7)

(8)

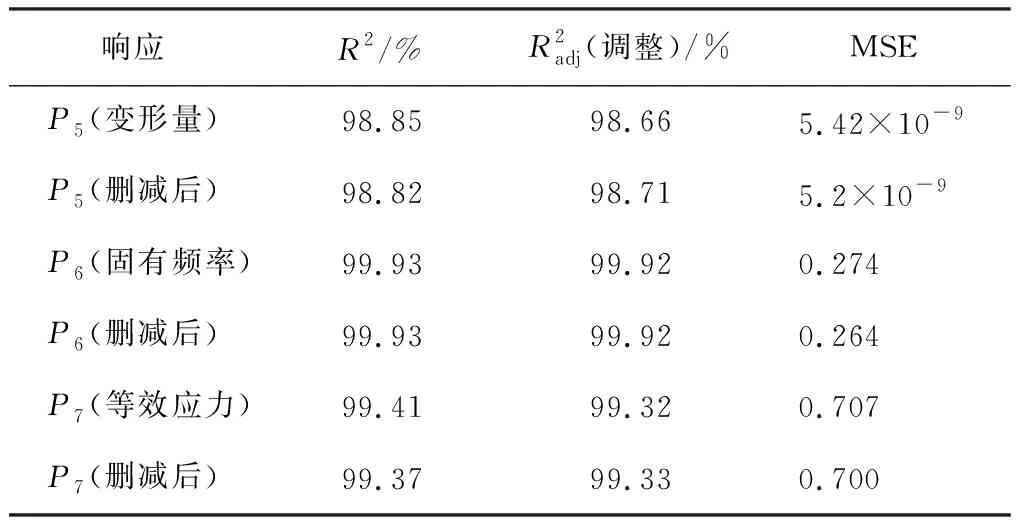
表2 拟合质量评估

2.3 GWO-BP代理模型

图7为狼群算法优化过BP神经网络对DOE数据模型进行拟合的流程图,拟合步骤大概分为3部分:数据预处理、狼群算法和BP神经网络。将DOE模型数据划分后进行归一化处理,筛选出隐含层神经元,得到没有优化神经网络的权值和阈值,选择BP神经网络的训练误差作为适应度函数,通过狼群算法特有的游走,召唤和围攻之后得到最佳适应度函数(即最小误差),将对应的权值和阈值代入原本的BP神经网络计算在此权值和阈值下的拟合精度。表3为优化后神经网络的拟合效果。

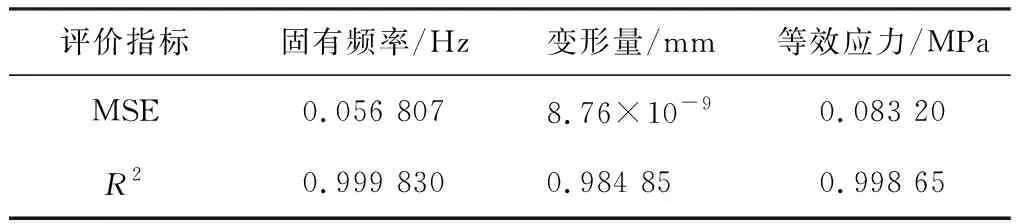
表3 优化后神经网络的拟合效果

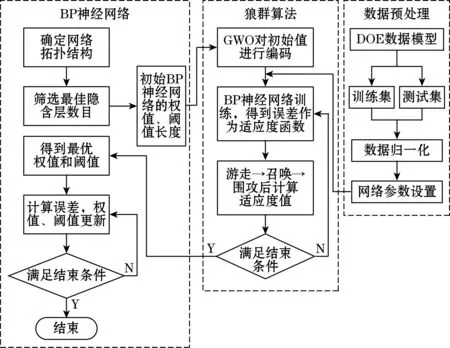
图7 GWO-BP拟合流程图

2.4 模型效果对比和混合模型搭建

通过表2和表3对比,对于固有频率,神经网络的拟合效果低于响应面模型,对于等效应力和变形量,神经网络的拟合效果优于响应面模型。使用CCD(中心复合实验)生成27组实验数据。分别用神经网络模型和响应面模型对27组数据进行预测,计算误差。

在不同拟合模型下,图8为变形量、固有频率、等效应力对应的预测误差,预测验证误差与上文提到的均方值误差对比验证的结果相同,神经网络的预测平均误差要高于响应面模型,对于等效应力和变形量,神经网络的预测误差要低于响应面模型。

图8 不同拟合应误差图

混合模型结构如图9所示。神经网络模型和响应面模型分别有各自的优点,现提出一种混合GWO-BP和响应面的代理模型,发挥各个拟合方式的优势,将变形量选用响应面模型,固有频率和等效应力选用神经网络拟合,组合成一个新的拟合模型。

图9 混合模型结构图

3 高维多目标优化分析

3.1 高维Pareto前沿面筛选

选用12种算法对混合代理模型进行寻优,算法分别如下[15]:AGEMOEA、ONEBYONE、SPARSEEA、RNSGAII、SMEA、LMEA、GFMMOEA、ARMMOEA、TOP、PEEA、MOPSO、NSGAII。得到三维Pareto前沿面,如图10所示,12种算法的Pareto前沿面基本相似,从3幅图中可以根据解的均匀性先进行筛选,其中不满足条件的解有如下6种:ONEBYONE、RNSGAII、SMEA、GFMMOEA、PEEA、MOPSO,以上算法生成的Pareto前沿不均匀,陷入了局部最优,无法保证解的均匀性。

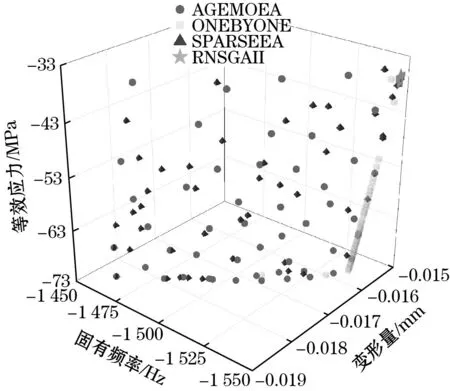
(a)AGEMOEA、ONEBYONE、SPARSEEA、RNSGAII的Pareto图

3.2 算法性能分析

由于其余6种算法无法通过直接比较判定解的均匀性和收敛性,本文选用IGD和HV 2个指标来定量的计算Pareto前沿各点的性能。

IGD的计算公式如下:

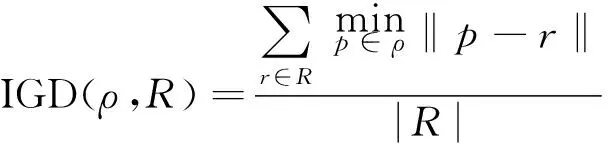
(9)

式中:ρ为待评价的点集;P为点集中的点;R为Pareto前沿的参考解集,r为其中的点;‖p-r‖为每个参考点到目标集中最近点的平均距离。

IGD数值越小代表ρ和R越接近,点集分布越均匀,IGD越大代表算法性能不好。

HV指标是需要评价的点集与参考点围成区域的超体积,超体积越大代表被评价的点集越收敛,分布越均匀,HV计算公式如下:

HV(ρ,R)=λ(H(ρ,R))
={z∈Z|∃p∈ρ,∃r∈R∶P≤z≤r}

(10)

式中:λ为勒贝格测度;R取远离Pareto前沿面的一组或多组解。

取上文筛选后的6种算法,分别生成100组前沿点,计算其IGD和HV指标,表4为6种算法的IGD和HV的平均值。从表4可以看出,质量最好的为SparseEA算法。

表4 不同算法性能对比

SPARSEEA[16]为求解大规模稀疏多目标优化问题的进化算法,旨在大量候选特征中挑选出小部分特征,该算法考虑到帕累托最优解的稀疏性,提出了一种新的种群初始化策略和遗传算子,以确保生成解的稀疏性。算法编码方式是实数变量和二进制变量相结合的方式,设实数变量为dec,二进制变量为mask,所以设计变量可以进行如下表示:

(x1,…,x4)=(dec1·mask1,…,dec4·mask4)

(11)

在种群初始化时,对得到的解进行非支配排序,将非支配前沿数作为这个解的得分,较高的得分代表解质量不高,这时二进制变量mask设置为0,那么得到的最终设计变量即为0。相反,最终决策变量即为原始数值dec。

3.3 泛化效果分析

从前沿面筛选出4个候选点,将其重新代入ANSYS中进行求解,计算与优化结果的误差,如表5所示。由表5可见误差最大为0.9%。表明混合代理模型拥有良好的泛化效果。

表5 候选点误差

从4组数据值中选择一组符合实际加工和满足应力范围的值进行圆整。从表5中挑选出最合适的尺寸,挑选过程中应注意,在满足性能需求下,HV的数值应尽可能取大值,IGD尽可能取小值。P1和P4应该尽可能取大值,因为P1、P3是孔边距离,过小的孔边距不容易加工。取点后进行圆整,最终确定P1=0.39 mm,P2=1.62 mm,P3=0.78 mm,P4=2.2 mm。表6为优化前后结果对比。优化后:固有频率降低5%,变形量提升14.7%,等效应力提升155%,结构最大应力为191 MPa。最大应力位置出现在打孔的边缘处,传感器材料的屈服强度为1 108 MPa左右,因此符合传感器应力要求。

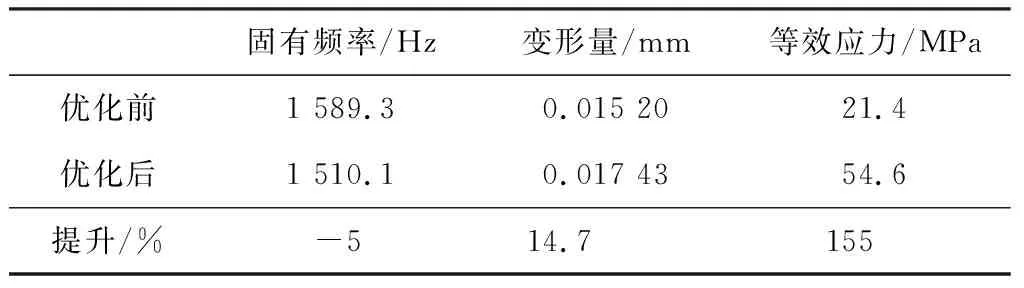
表6 优化前后结果对比

惠斯登全桥电路电压输出公式如下:

(12)

(13)

(14)

式中:U为输出电压;E为电桥供电电压;Ri为应变片电阻;ΔRi为Ri的电阻变化量;σ为应变片所在位置处的应力;Eu为弹性模量;K为应变片的灵敏度系数。

惠斯登全桥电路的4个应变片均作为敏感元件,其灵敏度是单臂电桥的4倍,根据变形量、应力提升幅度和式(8)～式(10),各向灵敏度提升6倍左右。

4 结束语

开孔位置的变化会改变传感器结构的危险截面位置,左侧周向布置的孔应靠近圆环。右侧周向布置的孔应远离圆环。高维空间的采样点在数量较低的情况下,中心偏差很大,随着采样点个数增加,偏差下降斜率会逐渐放缓,应根据实际仿真时间和效果精度选择合适的采样点个数。响应面模型针对变形量的预测效果更好,其余2个参数的预测效果神经网络模型更好,二次多项式的优化时间短且稳定,BP神经网络的优化时间多100倍且随机性大。