基于电涡流效应的绝对式直线位移传感器误差分析及抑制方法研究

吴玉龙,武 亮,李佩林

1.重庆理工大学机械检测技术与装备教育部工程研究中心;2.重庆理工大学时栅传感及先进检测技术重庆市重点实验室,重庆理工大学机械工程学院

0 引言

随着国内高端装备制造、芯片制造、航空航天等领域的发展,对绝对位移精密测量提出了更高的要求[1-4]。绝对式位移传感器可以直接读出位移的绝对值,没有累积误差,电源切除后位置信息也不会丢失。在实际应用特别是加工行业中,即使电源突然中断,也可立即从中断处读取位置信息。相比于增量式位移传感器,它可以更快速、精准定位,极大提高了加工效率[5-6]。直线位移传感器主要分电容式直线位移传感器、光学式直线位移传感器以及电磁感应式直线位移传感器[7]。电涡流位移传感器是电磁感应式传感器中的一类,采用非接触测量技术,具有灵敏度高、响应速度快、抗干扰能力强、可靠性好等优点[8-13]。Y.Fan等提出修正角误差法,采用交叉验证方法确定了误差模型中Maclaurin级数的合理阶数,提高了电涡流位移传感器角度的精度[14]。上海交通大学赵辉团队研制出基于电涡流效应的数字式涡流栅防水卡尺,采用定频调幅电路和交流电桥电路作为检测电路,在300 mm量程内测量精度可达±20 μm,分辨力10 μm[15-16]。

虽然电涡流传感器被越来越多的研究和使用,但相比其他类型传感器精度较低。因电涡流绝对式位移传感器的节距内误差大小直影响了传感器精度,所以采用一些有效的方法抑制传感器节距内误差便显得尤为重要[17]。文献[18]提出一种互补耦合型电磁感应式直线位移传感器,有效抑制了动定尺间隙变化、平行度差等装配问题对精度的影响。文献[19]对于平面磁场式绝对角度传感器的误差产生机理与抑制方法的描述,同样采用该方式抑制短周期误差。

因此,本文以基于电涡流效应的绝对式直线位移传感器为原型,对初步实验后各个频次的误差进行了溯源分析。首先介绍了传感器工作原理与结构;其次,对传感器1次、2次以及4次误差来源进行分析并提出相应的抑制修正方法;最后,搭建实验平台,对采用抑制方法后的传感器做短周期精度实验,验证了误差抑制方法的正确性。

1 传感器工作原理与结构

本文提出一种基于电涡流效应的绝对式直线位移传感器,结构如图1(a)所示。传感器由定尺和动尺组成,包含精机和粗机2个测量通道。其中粗机用于对极定位,精机用于确定传感器精度。定尺包含对应粗机的梯形金属导体(trapezoidal metal reflection conductor,TMRC)和对应精机的N个以等间距排列的矩形金属导体(rectangular metal reflection conductor,RMRC)。动尺包含激励线圈和感应线圈。传感器的位移可以通过处理感应电动势的变化得到。图1(b)和图1(c)中展示了精机5个典型位置的正余弦感应电信号,实线表示位移起始位置,虚线表示移动一个节距后的位置,通过反正切运算即可获得传感器位移。

图1 传感器结构图

粗机的激励线圈(field coil of the coarse measurement channel,Fc_F)和感应线圈(inductive coil of the coarse measurement channel,Ic_C)均为矩形螺旋线圈,直接排列在TMRC的正上方。精机的激励线圈(field coil of the fine measurement channel,Fc_F)为矩形螺旋铜线圈,感应线圈为正弦形铜线圈(sine inductive coil of the fine measurement channel,Ic_Fs)和余弦形铜线圈(cosine inductive coil of the fine measurement channel,Ic_Fc),Ic_Fs和Ic_Fc沿测量方向(X轴)错开W/4(W为1个空间节距)。

当激励线圈通入交变励磁信号I(t)=Asin(ωt)时,激励线圈周围将产生1个时变磁场Bs。其中,A和ω分别为励磁信号的幅值和频率。处于该时变磁场中的金属反射导体表面将产生电涡流,并向周围辐射1个新的涡流磁场Be,削弱原来的时变磁场Bs。在粗机中,梯形金属反射导体与线圈耦合面积随着位移增大而增大,其表面的电涡流也随之增大,感应线圈中的磁通量则线性递减;在精机中,金属反射导体表面的电涡流随位移产生周期性变化,与之对应,感应线圈中的磁通量也发生周期性变化。磁通量的变化引起感应电动势的变化,因此,精机的2路感应信号可以表达为:

(1)

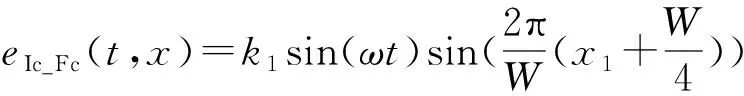
(2)

式中:x1为传感器动尺在单个节距内的位移,其变化范围为0～W。

采用鉴幅处理方式对2路感应信号进行处理得出位移x1的表达式为

(3)

在粗机中,梯形金属反射导体与传感单元的耦合面积随位移呈线性变化,因此,感应信号的幅值Ac也为线性变化,可以表示为

Ac=Kx2

(4)

式中:K为常数且K<0,随传感单元与金属反射导体的间隙变化;x2为定尺在量程内的粗位移。

Ac在量程范围内呈线性变化,因此可以确定动尺当前所处的对极位置。

(5)

式中:floor为向下取整函数;m为动尺当前所处位置的对极数。

结合精机中的位移x1,可获得传感器绝对位置xap。xap可以表示为

xap=(m-1)W+x1

(6)

2 传感器信号处理方法

传感器主要采用鉴幅原理的信号处理方法,如图2所示。利用ARM(型号:STM32F405)芯片的高级定时器输出互补的高频方波,经过谐振电路产生三路高频激励信号,再由感应线圈获取粗机和精机的2路电信号,经直流偏置、开关电路、滤波电路和运算放大器之后送入ARM的ADC模块。粗机的感应信号对对极位置进行了标记,上电即可获得当前对极位置,精机则通过反正切对正余弦信号进行鉴幅解算对极内位移,结合粗机和精机即可确定绝对位置。传感器通过Biss-C协议与电机驱动器通信。

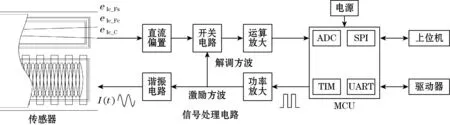
图2 传感器信号处理流程图

3 传感器误差分析及其抑制

因为粗机用于传感器的对极定位,其感应电信号的线性度决定了对极判断的准确性,而精机决定了传感器的定位精度和性能,其误差可认定为传感器的误差。由于传感器粗机的感应信号线性度较好,具有满足对极定位能力,下面主要分析精机对极内包含的各频次误差影响,并以此作为依据进行传感器的结构优化和误差修正。

3.1 节距内1次误差

传感器的1次误差主要由无效电动势引起,在理想情况下,当定尺不参与工作时,感应线圈中的磁通量为0。但存在传感器动尺加工制造和引线等环节不理想的情况,所以感应线圈中的磁通量无法完全抵消,此时存在的感应电信号为无效电动势。传感器正常工作时,包含无效电动势的感应电信号如式(7)、式(8)所示:

(7)

(8)

式中:k11sin(ωt)和k12sin(ωt)为无效电动势。

根据式(3)位移表达式可得:

(9)

将其与理想位移进行作差,得理论误差Δx为

(10)

理论误差Δx在1个节距内变化1次,当感应电信号存在无效电动势时,误差形式表现为1次。对于该误差,通过在反正切运算过程中补偿直流成分的方式来进行1次误差的抑制,当定尺不工作时,记录下此时模数转换后的值,即k11和k12的值;当定尺参与工作,即传感器样机正常工作时,将正余弦信号分别减去此时记录的值,从而减小或消除无效电动势对位移解算的影响。

3.2 节距内2次误差

根据传感器测量原理,经过模数转换后的2路正余弦感应信号应当严格正交且等幅,但由于传感器制造、安装、信号处理等环节可能存在问题,例如正余弦感应线圈制造时并非完全错开W/4,读数头安装发生了轻微偏转,运放电路电阻有偏差等。这些问题均会导致2路感应信号出现幅值不等或相位不正交的情况。

当两路感应电信号幅值不等时,其信号表达式可为:

(11)

(12)

式中:k21和k22为2路感应电信号的幅值,并且k21≠k22。

此时的位移可表达为

(13)

将其与理想位移进行作差,可得理论误差Δx为

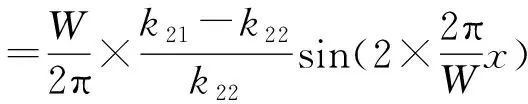
(14)

当2路感应电信号相位不正交时,其信号表达式为:

(15)

(16)

式中:Δφ为两路信号的相位差。

此时的位移可表达为

(17)

将其与理想位移进行作差,可得理论误差Δx为

(18)

由式(14)和式(18)可得理论误差Δx在一个节距内变化2次,当2路感应电信号存在幅值不相等或相位不正交的情况时,误差形式表现为2次。对于2次误差,主要采取补偿幅值的方式进行抑制。实验中,首先驱动读数头在量程内运动,获取并记录量程内的模数转换后的值,采用2路正余弦信号峰峰值的比值作为2次误差的补偿系数,并计算2路感应信号的中值,在传感器正常工作时,将AD转换分别先减去此前记录的中值,再将幅值较小的一路信号在计算时乘以该补偿系数以实现抑制2次误差的效果。

3.3 节距内4次误差

根据文献[20]研究结果,4次误差可由感应电信号的3次和5次谐波成分引起。忽略其他频次的误差,只取感应信号的基波、3次和5次谐波进行分析。令2路信号均为理想信号,所包含的各频次谐波成分幅值和相位均相等。包含基波、3次和5次谐波成分的感应电信号表达式为:

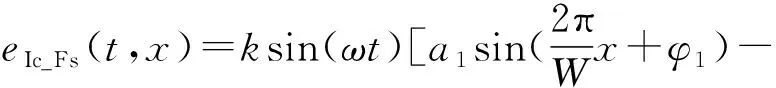
(19)

(20)

将其与理想位移作差,得理论误差Δx为

Δx=x2_2-x2

(21)

由式(21)可得理论误差在一个测量周期内变化4次,当用于位移解算的2路感应电信号中包含3次和5次谐波成分时,误差形式表现为4次。现阶段很难做到同时消除信号中的3次和5次谐波成分,由于3次谐波成分幅值远大于5次谐波成分幅值,所以目前先考虑消除3次谐波成分。可通过空间线圈移相的方式消除3次谐波成分,将精机的测量通道分为2部分,沿测量方向错开W/6,此时错开的正弦感应电信号分别为:

(22)

(23)

将错开的感应线圈串联,叠加后的正弦感应电信号为

(24)

由式(24)可得,进行空间移相后的正弦感应信号中不再包含3次谐波,余弦感应信号同理,以此抑制传感器的4次误差。

4 传感器样机实验

4.1 实验平台与样机

将仿真验证后的传感器模型通过印刷电路板(printed circuit board,PCB)技术加工出来,制作的实验平台如图3(a)所示。实验装置均置于大理石平台上,以单轴直线电机(LM135-F414-850-C05-A)和伺服驱动器(CDHD-4D52AEC2)为驱动装置,采用XL80激光干涉仪进行标定。实验中,传感器样机的读数头、激光干涉仪反光镜与电机滑台保持同步运动,通过比对传感器样机和激光干涉仪的位移数据得出传感器误差数据。

(a)实验平台

动尺和定尺相关制造参数如表1所示,实物如图3(b)和图3(c)所示。

表1 PCB技术制造参数

定尺为双层板,整长为516 mm,有效量程为500 mm,宽24 mm,厚2 mm。选择铜作为金属反射导体,矩形金属反射导体的尺寸为14 mm×2 mm,梯形金属导体的尺寸为(0.5 mm+4.5 mm)×516 mm,铜厚均为1 oz(1 oz=35 μm)。动尺同为双层板,通过过孔完成线圈的交替排布,正余弦线圈形状完全相同,在空间上沿测量方向错开W/4。

4.2 初始误差实验结果

完成传感器信号调试之后,在传感器4 mm节距内和500 mm量程内进行精度实验,实验结果如图4所示,误差峰峰值约为32 μm,对其进行傅里叶分解得到误差曲线的谐波频次,主要包含1次、2次和4次误差。传感器粗机在500 mm量程内的误差峰峰值为49 μm,满足粗机定位要求。

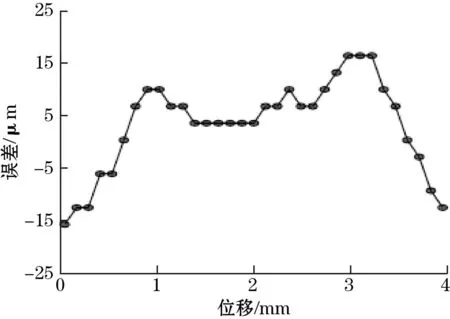
(a)节距内误差

4.3 误差抑制后实验结果

根据前期课题组对该传感器的研究与验证,在4 MHz激励下,控制动定尺轴向间隙为0.5 mm时,传感器的节距内误差较小。因此,以下实验将在该条件下进行。

4.3.1 1次误差的抑制

根据前文公式的推导,1次误差主要来源于式(10)中的直流成分k11和k12。为了提高传感器精度,减小感应线圈中的无效电动势的影响,采用补偿直流分量的方法抑制1次误差。具体实验方法如下:首先,传感器在无定尺后上电,此时,获取感应电压模数转换后的值并存储在MCU的Flash中,记为k11、k12。其后,在有定尺情况下,对采用信号补偿方法(正余弦信号分别减去k11和k12作反正切)的传感器进行对极内精度测试。在4 mm测量范围内每间隔0.125 mm采样1个点作误差曲线,其误差实验结果如图5所示。优化后传感器对极内的误差曲线如图5(a)所示,节距内误差峰峰值约为15 μm,较优化前明显减小。如图5(b)所示,对极内的1次误差显著减小,2次和4次误差也得到了减小。

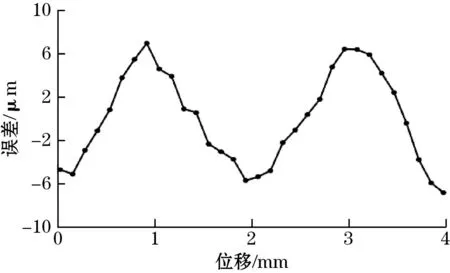
(a)节距内误差

4.3.2 2次误差的抑制

对于2次误差的抑制,主要对正余弦其中一路的信号幅值进行补偿。具体实验方法与1次误差的抑制方法类似。首先,使用电机驱使传感器完成一次全量程的运动,采集模数转换后2路正余弦信号的幅值较大值Amax和幅值较小值Amin。将Amax和Amin的比值作为2次误差的补偿系数并存储在MCU中。样机开始正常工作时,会在程序里将幅值较小的一路信号乘以该补偿系数,使正余弦幅值近似相等。在与1次误差抑制相同的实验条件下,得到其误差实验结果,如图6所示。优化后传感器对极内误差曲线如图6(a)所示,节距内误差峰峰值约为10 μm。如图6(b)所示,对极内的2次显著减小,而表现较为明显的4次误差。

(a)节距内误差

4.3.3 4次误差的抑制

在进行1次、2次误差抑制的基础上,采取空间移相方法,将感应线圈沿测量方向错开W/6,优化后传感器具体结构如图7所示。

图7 优化后传感器结构

对优化后的传感器进行对极内精度实验,得到误差实验结果如图8所示。优化后传感器对极内误差曲线如图8(a)所示,节距内误差峰峰值约为6 μm。如图8(b)所示,传感器对极内的4次误差显著减小。

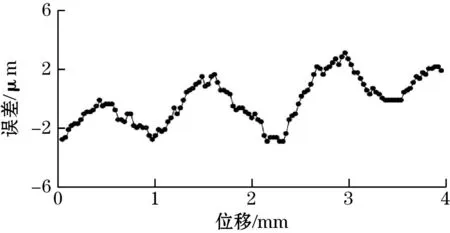
(a)节距内误差

进行了抑制实验后的传感器,各个频次的误差显著降低,其性能大幅提升。

5 结束语

本文基于电涡流效应的绝对式直线位移传感器的样机实验,分析了因其制造、安装及引线过程不理想而出现的节距内各个频次的误差,并对其1次、2次及4次误差给出了相应的抑制方法。在样机的信号处理环节,使用信号补偿方法对节距内1次和2次误差进行了抑制。抑制了1次误差后,样机节距内误差减少了约1/2;在此基础上,抑制了2次误差后,节距内误差峰峰值为10 μm。最终,在优化了动尺结构并减小了4次误差的情况下,节距内误差峰峰值约为6 μm。虽然相比未经抑制处理的样机前精度已有很大提升,但从其节距内误差曲线规律仍然可以看出有着较明显的4次误差,也包含了1次和2次的误差成分。在后续的研究中,可以通过结构的优化与信号的处理进一步提升传感器性能。