焊接平台龙门架结构轻量化设计
2024-04-27陈国雄吴家雄张大斌
陈国雄,曹 阳,3,吴家雄,张大斌,3
(1.贵州大学机械工程学院,贵州 贵阳 550025;2.中建四局安装工程有限公司,贵州 贵阳 550000;3.贵州省机电装备工程技术研究中心,贵州 贵阳 550025)
1 引言
角钢法兰焊接平台是自动化生产消防通风管道连接法兰的专用设备,具有操作简单、精准定位、焊接效率高及成本投入低等优势,适用大批量生产不同规格的角钢法兰。自行研制的角钢法兰焊接平台,采用龙门架实现双工位衔接工作,根据传统经验设计得到的龙门架结构,其设计变量对结构的质量、刚度、1阶模态频率及最大等效应力等均会产生不同程度的影响[1-2],如在承受载荷及外部激振的作用下,龙门架变形量大、振动较明显,在焊接过程中易造成焊丝偏离焊缝中心线,从而导致焊缝成形质量差、工作稳定性低等问题。因此,需对龙门架结构进行优化设计,以提高角钢法兰焊接平台的焊接稳定性。
由于龙门架具有工作平稳、安全可靠及开敞好等优点,因而被广泛应用于加工制造等行业的各类设备中。目前大多学者主要通过对龙门架结构进行优化研究来提高机器性能。文献[3]通过对常见的四种龙门结构模型进行静动特性分析,提出一种基于三心拱的新型龙门结构,并对其结构的高度和跨度参数进行了优化设计,缺乏考虑其它设计变量对龙门架结构性能的影响;文献[4]通过增加龙门架横梁结构“米”字型筋板的数量并对其设计变量进行优化以提高整体性能,该方法优化效果不明显,且增加制造成本。
为了达到轻量化设计,文献[5]对横梁关键尺寸进行静动态特性灵敏度分析,利用极端尺寸调整法,实现单性能指标轻量化的基础上,得到最佳轻量化设计方案,该方法在优化求解过程计算量大,凭借经验对设计变量进行调整求解,但缺乏科学性指导。
以自行研制的角钢法兰焊接平台龙门架作为研究对象,借助ANSYS有限元软件对其进行静、动态特性分析。通过建立龙门架结构设计变量与各性能指标的优化模型,对其进行多目标优化的轻量化,并将优化后的结果进行静、动特性对比验证,从而得到龙门架优化设计后更为合理的结构。
2 龙门架设计要求及优化流程
2.1 焊接平台结构及龙门架设计要求
焊接平台由龙门架、二氧化碳气体保护焊枪、Y向丝杠滑台传动装置、Z向丝杠滑台式传动装置、X向丝杠滑台式传动装置、气动式夹具、精准定位板、焊件载台及床身等部件组成,可焊接不同规格形状(如矩形、U形和L形)的角钢法兰,焊接平台整机结构,如图1所示。

图1 焊接平台整机结构图Fig.1 Welding Platform Structure Diagram
龙门架作为焊接平台的重要关键承载部件之一,其静、动态力学性能对整机工作质量有较大影响。工作时,龙门架会受到各种外部振动激励的影响而发生共振现象,尤其龙门架与焊枪之间的相对变形会直接影响到焊接平台对角钢法兰的焊接精度或质量。
因此,对设计的龙门架结构应要求尽可能避开所有外部激励频率的影响,以免发生共振现象而导致整机焊接性能严重下降,且在满足工作性能条件下,龙门架还应力求质量轻盈。
2.2 龙门架优化流程
本研究基于有限元法+近似模型+遗传算法的优化方法,通过建立龙门架处在极端垂向载荷工况下的有限元模型,以龙门架的刚度、强度、模态特性及质量为目标函数或约束条件,对龙门架的轻量化研究,优化流程,如图2所示。
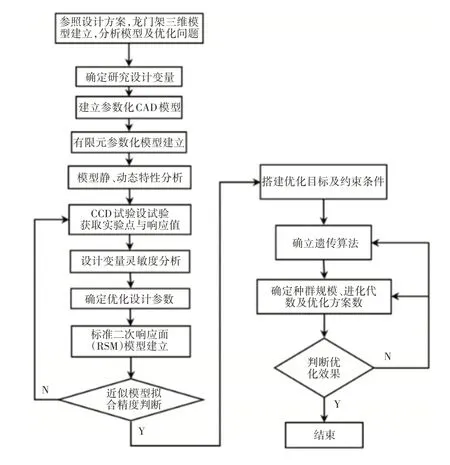
图2 龙门架结构优化流程图Fig.2 Gantry Frame Structure Optimization Flow Chart
3 龙门架有限元分析
3.1 有限元前处理
建模时,仅需抓住研究对象问题的本质,并对原始模型进行适当简化,有利于提高仿真效率及质量。龙门架上立柱盖和横梁盖均采用厚度为2mm的薄钢板制成,主要起防尘保护作用,进行有限元建模时,可忽略。龙门架主要由立柱和横梁拼接后焊接制成,均采用5mm钢板折弯而成。
因主要关注龙门架整体结构的特性研究,而非关注局部的焊缝问题,在ANSYS 环境下,可将立柱与横梁接触关系简化为Bonded形式,用以模拟各部件之间的焊接关系(即力传递方式),此简化方式对所关注的有限元特性结果保真的同时,能较大程度地提高求解速度,有助于后续试验设计中大量试验样本点的仿真求解过程。
龙门架材料为Q235 碳素结构钢,材料属性为:弹性模量(2.1×1011)Pa,质量密度7850kg∕m3,泊松比0.3。采用自适应网格划分法对其进行网格划分,节点数190480,单元数77896个。
龙门架作为各执行机构和零部件的关键承载部件,主要受到垂向力外部载荷有焊枪座及其以上所有部件的重力,还有横梁两端步进电机及其附属机构、部件的重力。当两个焊枪处于横梁中间位置时,龙门架所产生的变形最为严重。龙门架底端采用螺栓与滑动连接板,故此处施加固定约束。
前、后闭环步进电机驱动装置等部件对横梁总载荷均为48N;左、右焊枪驱动组件对横梁总载荷均为197N;焊枪上下移动运动过程中,会对龙门架具有一定的影响[6],根据静载荷Q与动载荷F关系有:
式中:K—动载荷系数,此处取1.2。
经式(1)计算得动载荷F为236.4N。故龙门架结构所承受的极端垂向载荷及约束位置分布,如图3所示。

图3 龙门架承受极端垂向载荷与约束位置分布Fig.3 Distribution of Extreme Vertical Load and Constraint Position of Gantry Frame
3.2 静力学分析
根据龙门架承受如图3所示垂向载荷作用与约束条件下,求解得龙门架的静变形云图,如图4所示。

图4 龙门架静变形云图Fig.4 Static Deformation Cloud Image of Gantry Frame
由图4可看出龙门架最大变形量约为0.1034mm,其位置位于横梁低板、侧边中部。最大变形常以载荷中心的垂直静挠度作为计算值,垂直静挠度值反应刚度性能强度[8],即:
式中:[f]—许用静挠度;L—横梁长度。
由于横梁的长度为1218mm,根据式(2)可计算出龙门架的许用静挠度为1.218mm,而龙门架的最大静变形量0.1034mm,远小于许用挠度值,说明当前龙门架满足刚度设计要求,且存在较大的刚度冗余。龙门架的等效应力云图,如图5所示。

图5 龙门架等效应力云图Fig.5 Equivalent Stress Nephogram of Gantry Frame
对龙门架结构应力特性研究可由材料的许用应力来进行评价,许用应力[σ]计算公式为:
式中:σs—材料屈服应力;ns—安全系数。
根据龙门架材料σs=235MPa;考虑到龙门架作业环境及工况,取ns=1.5,计算出[σ]=156.67MPa。由图5可知,龙门架的最大等效应力为8.67MPa,远低于材料的许用应力[σ]=156.67MPa,说明当前龙门架结构符合强度要求,且材料存在较大富余。因此,可对龙门架结构展开轻量化研究。
3.3 模态分析
模态是结构在确定材料属性及形状后所具有振动频率和模态振型,对结构进行模态分析,有利于寻找到刚度不足或相对薄弱的位置,可为结构优化提供指导作用[9]。笔者先通过对龙门架进行约束模态计算,共提取龙门架结构前六阶模态频率及振型,如表1所示。

表1 龙门架前6阶模态频率及振型Tab.1 The First 6 Order Modal Frequencies and Mode Shapes of the Gantry Frame
龙门架承受的外部振动激励主要包括Y向和Z向直线滑块机构中闭环步进电机运转而产生的激励作用。龙门架上4台闭环步进电机正常工作允许的最高转速n为1250r∕min,激振频率f计算为:
经计算得到闭环步进电机工作时产生的激振频率f为(0~20.83)Hz,而当外部激振频率在构件固有频率的(85~115)%范围内时,计算频率为(20.8~28.14)Hz,将会对构件产生影响[11]。由计算可知该激振频率在共振带范围内,故存在发生共振的可能性。因此,有必要对龙门架结构的1阶模态频率进行优化。
4 龙门架近似模型建立
4.1 确定设计变量及性能指标
为建立分析软件之间的数据接口,需对模型设计尺寸进行参数化,即在尺寸前添加“DS_”前缀。根据焊接平台龙门架结构特征,以立柱板厚P1、立柱宽P2、立柱长P3、横梁高P4、横梁折弯余边P5、横梁板厚P6及横梁宽P7作为设计变量(即输入参数),以最大静变形量Q1、最大等效应力Q2、质量Q3、1阶模态频率Q4为性能指标(即响应值)。龙门架各尺寸参数位置分布情况,如图6所示。
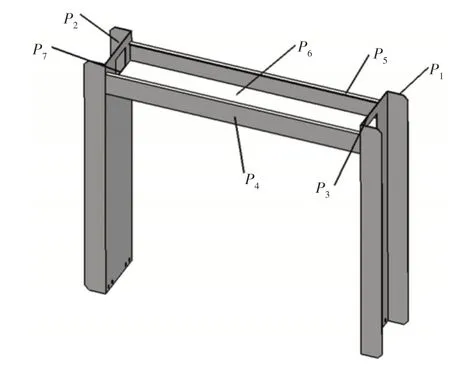
图6 龙门架各尺寸参数的结构位置分布情况Fig.6 Structural Position Distribution of Each Dimension Parameter of the Gantry Frame
根据安装在龙门架上的其它零部件外形尺寸对龙门架结构尺寸的约束,确定各设计变量的初始值及取值范围,如表2所示。

表2 龙门架设计变量初始值及取值范围(mm)Tab.2 Initial Value and Value Range of Gantry Frame Design Variables(mm)
4.2 DOE试验设计
由于中心复合试验设计方法CCD(Center Composite Design)能以较少的试验循环即可获取试验变量和试验误差的诸多信息情况。因此,采用CCD试验设计,选择Auto Defined类型,对龙门架有限元模型进行7因素5水平的中心复合试验设计,共提取到79组试验样本及响应值,如表3所示。

表3 CCD试验试验样本及响应值Tab.3 CCD Test Samples and Response Values
4.3 灵敏度分析
通过ANSYS Workbench响应面优化模块提取得到龙门架结构中7个设计变量分别对应最大静变形量、1阶模态频率、质量及最大等效应力4个性能指标的灵敏度显著情况,如图7所示。

图7 设计变量对应各性能指标灵敏度Fig.7 Design Variables Correspond to the Sensitivity of Each Performance Index
由图7可得:(1)P7与最大变形量呈正相关,其余变量与最大变形量呈负相关,而且P5对最大变形量显著性最小;
(2)P1、P2、P5、P7与最大等效应力呈正相关,其余与最大等效应力呈负相关,而且P5对最大等效应力显著性最小;
(3)所有变量对总质量的显著性均呈正相关,而且P5总质量的显著性也最小;
(4)P6、P7与1阶模态频率呈负相关,其余变量与1阶模态频率呈正相关,而且P5对1阶模态频率显著性最小。综上所述,P5对各性能指标的影响程度最小,故将P5剔除不再参与后续优化研究,仅默认为初始值。
4.4 响应面模型构建与验证
由于通过对有限元模型的直接优化成本较高,因此,在实际工程优化问题中,为减少仿真优化求解所消耗的时间,快速提高仿真优化效率,通常可采取近似模型(亦称为代理模型)以代替实际的物理试验或仿真试验进行优化分析。目前,构建近似模型的常用方法主要有响应面模型(RSM)、克里金(Kriging)模型、径向基函数(RBF)模型等等,其中:响应面模型具有数学表达式简单,计算量较小的优点,广泛应用于各领域的优化问题分析。因此,笔者通过在前述中心组合试验得到的79组试验样本点及对应响应值的基础上,采用二阶多项式响应面法构建近似模型,具体公式如下[12]:
式中:y(x)—拟合函数;
xi—设计变量,i=1,2,…,n;
α0,αi,αii,αij—待定系数;
ε—精度误差。
由于文章篇幅所限,仅展示出每个目标函数与其对应较为敏感参数之间的响应曲面图,如图8所示。响应面模型的有效性受其拟合精度的直接影响,为了判断所构造的二阶多项式响应面模型是否能够代替实际工程真实模型(指物理试验或仿真试验),并用于后续优化问题求解研究,在使用前,需对所构造的响应面模型进行拟合精度检验。在实际工程应用中,主要是通过决定系数(R2)来评价响应面模型的拟合精度是否符合要求的。

图8 响应曲面Fig.8 Response Surface
决定系数(R2)的取值范围在[0,1]之间,当R2值越趋近于1时,则表明拟合得到的响应面模型精度就越高,反之越低[13],对R2的计算可按如下公式:
式中:yi—测试点的真实值;
—近似模型对测试点的预测值;
—真实值的平均值。
经式(7)求解得到二阶多项式响应面模型的拟合精度,如表4所示。

表4 响应面拟合精度Tab.4 Response Surface Fitting Accuracy
根据表4可知,龙门架4个目标函数(性能指标)与6个关键设计变量之间的拟合精度值均大于0.93,而一般工程要求响应面模型的决定系数R2不得低于0.9。
上述研究表明:通过二阶多项式响应面模型拟合法得到的近似模型能代替实际真实模型(此处指龙门架仿真试验有限元模型)。
5 龙门架多目标优化研究
5.1 多目标优化数学模型的建立
根据前面拟合建立的龙门架二阶多项式响应面模型,将龙门架质量Q3作为需优化的目标函数,以龙门架最大静变形量Q1、最大等效应力Q2、1阶模态频率Q4为约束条件,以筛选后得到的P1~P4、P6、P7共6个关键尺寸作为目标函数的自变量,共同建立起龙门架多目标优化数学模型如下:
5.2 多目标优化模型求解及结果对比分析
对于多目标问题的求解方法主要有归一化方法和非归一化方法。加权法作为多目标归一化算法的代表,具有把多目标函数转化为单目标函数来求解的优点,但各目标之间的权值不易设定,通常受到优化决策者主观因素影响较大;而多目标遗传算法(MOGA)作为多目标非归一化方法的典型代表算法之一,其能够快速排序非支配解和种群多样性,是目前多目标优化问题求解中最有效的全局优化算法之一。笔者在上述所建立的响应面模型基础上,利用多目标遗传算法对龙门架多目标优化数学模型进行求解,对该算法详细参数设置,如表5所示。

表5 遗传算法优化参数设置Tab.5 Genetic Algorithm Optimization Parameter Setting
由于多目标优化问题的全局最优解通常并不唯一的,而是由多个最优解组成的集合,也称为Pareto最优解集。因此,对所建立的响应面模型求解后,在Ansys优化模块Candidate Points中得到3组候选方案,如表6所示。
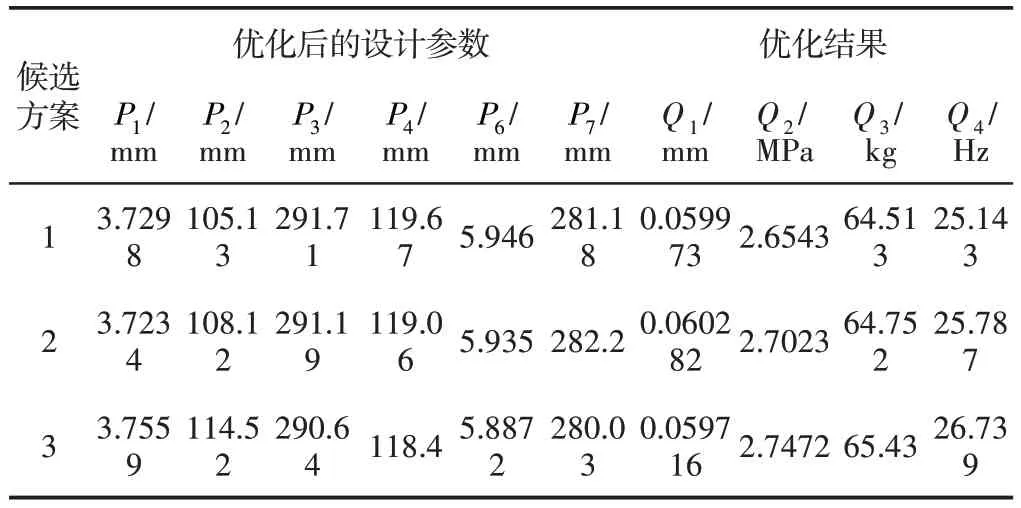
表6 设计参数优化结果候选组合Tab.6 Candidate Combination of Optimization Results of Design Parameters
表6为软件平台求解后给出的较为合理的优化设计参数结果,综合考虑龙门架的加工制造工艺后,决定选择方案3作为最佳参数参考。将龙门架优化后得到的设计变量最优解进行圆整修正,再次对该组尺寸参数下的龙门架有限元模型进行静、动态特性分析,获得优化前后龙门架各设计尺寸对应的性能指标结果,如表7所示。

表7 龙门架优化前后参数对比结果Tab.7 Performance Comparison Results of Gantry Frame Before and After Optimization
由表7可得,优化后的龙门架质量减少了7.34%,最大静变形量增加了0.0434mm,1阶模态频率增加了1.22Hz,避开了激振频率范围,最大等效应力增加了4.16MPa,仍远小于许用值,优化效果较明显,该方法适用于较为复杂结构分析与优化具有一定的指导意义。
6 结论
(1)建立了龙门架在Solidworks 与ANSYS 联合下的有限元参数化模型,通过对龙门架进行静、动特性分析,得到了龙门架优化前的力学性能,为优化提供重要依据。
(2)结合中心复合试验设计与灵敏度分析研究了龙门架结构参数分别对总重量、最大静变形量、最大等效应力和1阶模态频率的显著性,筛选得到了龙门架的关键设计变量。
(3)结合响应面法近似模型技术和遗传算法,对龙门架进行多目标优化,获得了Pareto最优解集,并确定了龙门架结构最佳优化设计方案。
(4)通过龙门架优化前后仿真分析对比,结果表明:龙门架总体质量下降,且1阶固有频率有所提升,避开了共振频率,整体改善了龙门架结构的力学性能。
