合理表征、整体建构“相遇问题”模型

陈诚

模型意识是小学数学核心素养的主要表现之一。《义务教育数学课程标准（2022年版）》指出：“模型意识主要是指对数学模型普适性的初步感悟。知道数学模型可以用来解决一类问题，是数学应用的基本途径；能够认识到现实生活中大量的问题都与数学有关，有意识地用数学的概念与方法解释这些问题。”模型意识与几何直观、符号意识、应用意识等核心素养密切相关。模型意识的培养有其综合性和复杂性，教师应结合学情，综合运用多种直观教学手段，帮助学生清晰地表征数量关系，并适度开展跨学科主题学习，帮助学生体悟数学模型的普适性，增强应用意识。下面，笔者以“相遇问题”的教学为例，分析建模过程。

一、创设情境，提炼数学问题

蔡金法教授指出：“数学建模实际上是一个从‘现实情境转化为‘数学问题，再将结果带回到‘现实情境进行检验和调整，使得模型不断优化，最终得以更好地解决现实问题的过程。”真实的情境是数学建模的基础，能迅速唤醒学生的生活经验，激发学生的探究欲。教学“相遇问题”时，笔者创设了如下情境。

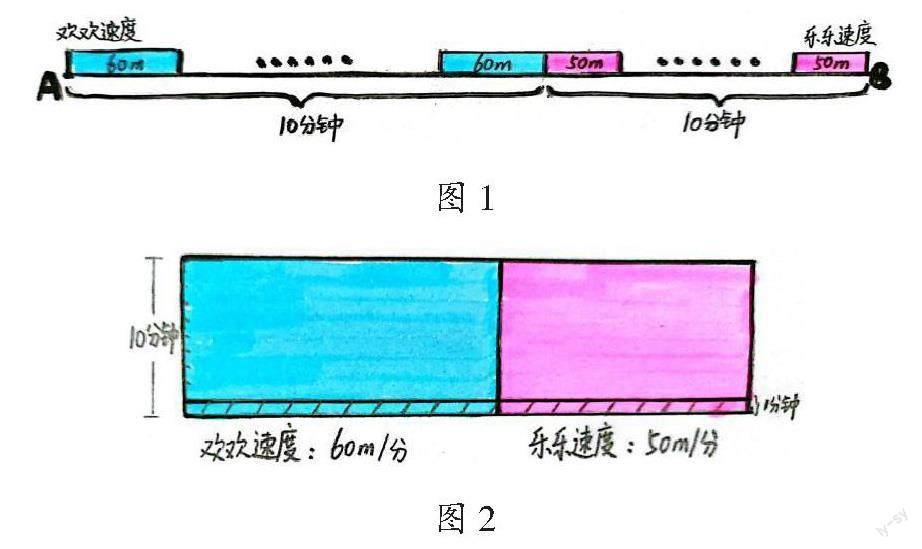
欢欢和乐乐对身体上的“尺子”很感兴趣，他们想通过步行测量两家大约相距多少米，于是一起做了一个小实验。首先，他们测量出各自平均每分钟走的路程，欢欢测得自己平均每分钟走60米，乐乐测得自己平均每分钟走50米。然后，他们约定同时从各自家里出发，走同一条路前往对方家。步行10分钟后，他们相遇了。你知道欢欢家和乐乐家相距多少米吗？

笔者提供这个情境后，学生的探究欲一下子被激发出来。笔者引导学生提炼情境中的数学信息，抽象出如下数学问题：“欢欢和乐乐同时从家里出发，相向而行。欢欢每分钟走60米，乐乐每分钟走50米，10分钟后相遇。欢欢家和乐乐家相距多少米？”通过这一转化过程，学生将数学与生活紧密联系起来，为后续模型的建立奠定了基础。

二、深入探究，抽象数学模型

明晰数学问题后，教师应引导学生完整经历数学模型的抽象过程。抽象过程中，分析、理解和表达数量关系是数学建模的重要一环，有助于学生明晰解决问题的思路。几何直观是帮助学生分析和理解数量关系的重要思想方法，教学“相遇问题”时，笔者通过图示等直观的表征方式，引导学生观察、比较、分析数量关系，进而用数学语言抽象、概括数学模型。

笔者布置如下探究活动：①画一画——根据题意画图分析；②想一想——自主思考怎样解答；③说一说——分享为什么这样解答，以及有什么发现。首先，学生用蓝色小长方形代表欢欢每分钟步行的路程（速度），用粉色小长方形代表乐乐每分钟步行的路程（速度），画出图1，并发现A到B之间的长度即为两家的距离。同时，由于两人步行的时间相同，所以学生将图1中的时间纵向叠加，进一步抽象出图2。图2中，蓝色长方形的长代表欢欢每分钟步行的路程（速度），粉色长方形的长代表乐乐每分钟步行的路程（速度），长方形的宽则代表两人步行的时间。

其次，在“想一想”的活动中，学生结合图2分析得出“欢欢步行路程=欢欢步行速度×时间=60×10”，即为蓝色长方形的面积。同理，乐乐步行路程=乐乐步行速度×时间=50×10，即为红色长方形的面积。因此，两人步行的路程即为两个长方形的面积之和（大长方形的面积），也就是可用“（60+50）×10”得出欢欢家和乐乐家相距1100米。

最后，在“说一说”的活动中，学生结合图2进一步阐释算式的意义，发现“60+50”即图中斜线部分的面积，表示“两人每分钟步行的距离（两人的速度和）”，步行10分钟，即10个“60+50”相加。由此，学生归纳出：（甲速度+乙速度）×相遇時间=相遇路程。这一模型结构与乘法模型一致。其中，“60+50”相当于乘法中的每份数，“10”代表份数，“1100”代表“总数”。

在这一过程中，学生通过图示表征、数形结合等方法，构建出解决相遇问题的直观“面积模型”，把握了“相遇问题”的本质——乘法模型（每份数×份数=总数），明晰了“先求两人步行的速度之和，再乘两人步行的时间，得到两人相距路程”的思维路径，进而提炼出解决相遇问题的一般数学模型——（甲速度+乙速度）×相遇时间=相遇路程。

三、沟通联系，整体建构模型

在新的数学模型建立后，教师应引导学生联系已掌握的数学模型，通过寻找新旧模型之间的内在逻辑关系，使头脑中的“单一模型”发展为“多元模型”，从而丰富模型结构，整体建构模型。

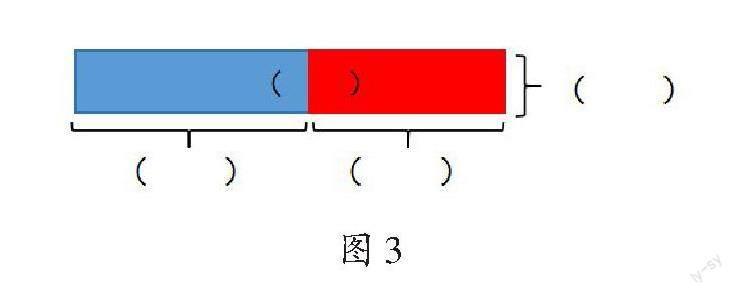
在具体情境中，“速度×时间=路程”“单价×数量=总价”“工作效率×工作时间=工作总量”这三个模型均与“每份数×份数=总数”相关，均属于乘法模型。基于此，笔者在学习单中设置了一系列问题，帮助学生丰富模型结构，整体建构模型。问题1：学校要为体操队的10名学生购买体操服，已知上衣的价格是60元，裤子的价格是50元，一共要用多少钱？问题2：平平每天练习写60个毛笔字，安安每天练习写50个毛笔字，10天后，两人一共写了多少个毛笔字？笔者让学生按照学习单上的要求，思考图3各部分分别可以代表问题1和问题2中的哪些信息，并将相应的信息填写在括号中，最后计算解答问题。

通过以上学习活动，学生发现：在上述问题情境中，无论是求解“相遇路程”，还是求解“总价”“工作总量”，都能用算式“（60+50）×10=1100”表示，并且题目中的数量关系都可以用面积模型表征。换言之，“（甲速度+乙速度）×时间=路程”模型、“（甲单价+乙单价）×数量=总价”模型、“（甲工作效率+乙工作效率）×工作时间=工作总量”模型本质上是相同的，如果用字母表示，均可表示为[（a1+a2）×b=f]。这样学习，学生沟通了模型之间的联系，对数学模型形成了更加抽象的理解，初步感知到数学模型的普适性。

四、注重变式，深入解构模型

整体建构数学模型之后，教师要通过变式问题，强化学生对数学模型与原型之间联系的感悟，促进学生头脑中数学模型的结构化。具体来说，在学生建构“[（a1+a2）×b=f]”数学模型之后，笔者通过变换具体问题情境中的条件和问题，形成如下变式问题。

变式1：欢欢家和乐乐家相距1100米，他们同时从家出发，相向而行，10分钟后相遇，已知欢欢每分钟步行60米，乐乐每分钟步行多少米？

变式2：学校为10名学生购买体操服（含上衣和裤子），共花费1100元，已知每件上衣50元，每条裤子多少元？

变式3：平平和安安制定了共同写1100个毛笔字的目标，她们从同一天开始书写，已知平平每天写60个毛笔字，安安每天写50个毛笔字，她们几天能写完？

学生分析解答、交流讨论后发现：虽然求解这三道题目的算式与原型不同，但这三道题目的数量关系与原型一致，均为“[（a1+a2）×b=f]”模型。这样教学，学生在变式训练中解构模型，形成了对数学模型的结构化认知。

五、联系生活，凸显应用价值

学生整体建立对数学模型的结构化认知后，教师应提供一些现实问题，帮助学生提升数学模型的应用水平。笔者给出如下凸显数学模型应用价值的挑战性任务，引导学生在识别模型、解决问题的过程中加深对数学模型的理解。

下面的问题能用数量关系“[（a1+a2）×b=f]”表达吗？若能，请说一说题目中的[a1]、[a2]、[b]和[f]分别表示什么？

问题1  学校要为图书馆添置两种新书，每种买4套。其中，故事书每套145元，科技书每套155元。一共要花多少钱？

问题2  甲、乙两队合作修一条隧道，从两端同时开凿。隧道长1200米，10天打通。已知甲队的进度是70米/天，乙队的进度是每天多少米？

问题3  小华家和小丽家相距2500米，他们同时出发，相向而行。小华每分钟骑行260米，小丽每分钟骑行240米。幾分钟后他们可以相遇？

学生独立思考、小组交流后，笔者组织学生汇报。第一小组汇报：问题1为“总价模型”，[a1]、[a2]分别代表故事书和科技书的单价，即145元、155元；[b]代表数量，即4套，是已知量；[f]代表两套书的总价，是未知量；列式“（145+155）×4”，求得[f]为1200元。第二小组汇报：问题2为“工作总量模型”，[a1]、[a2]分别代表甲、乙两队的工作效率，即70米/天和“未知量”；[b]代表工作时间，即10天；[f]代表工作总量，即1200米；根据模型列式“（70+[a2]）×10=1200”，求得[a2]为50米/天。第三小组汇报：问题3为“相遇问题模型”，[a1]、[a2]分别代表小华和小丽的骑行速度，即260米、240米；[b]代表两人相遇的时间，是未知量；[f]代表路程，即2500米；根据模型列式“（260+240）×[b]=2500”，求得[b]为5小时。完成这一任务后，笔者引导学生根据“[（a1+a2）×b=f]”模型，拓展创编不同的数学问题。

（作者单位：武汉市光谷豹子溪小学）

责任编辑  刘佳