虚拟惯量控制对直驱风电机组载荷影响的分析及评估

2024-04-22李东翰雷显帅李海啸

电力系统自动化 2024年7期

杨超，李东翰，雷显帅，李辉，李海啸，刘静

（1.重庆市能源互联网工程技术研究中心（重庆理工大学），重庆市 400054；2.输配电装备及系统安全与新技术国家重点实验室（重庆大学），重庆市 400044；3.中国船舶集团海装风电股份有限公司，重庆市 401123）

0 引言

伴随“碳达峰·碳中和”和“构建以新能源为主体电力系统”战略目标的提出，电力系统中风电接入比例快速攀升，系统惯量降低、调频能力减弱等问题凸显［1-3］。为保障风电大规模接入后系统安全稳定运行，各国风电并网标准均对风电提出了支撑电网的要求，中国最新风电并网标准也对风电提出惯量支撑的要求［4-7］。然而，惯量控制会改变风电机组出力特性，进而对机组机械载荷产生不可忽视的影响。因此，开展惯量控制对风电机组机械载荷的影响研究，对提高未来新型电力系统中并网风电机组的机械可靠性具有重要意义。

当前，针对风电机组载荷分析和控制，国内外已开展较多研究［8-10］。文献［11］通过获取塔筒振动模型及其动态参数，设计了降低风、浪联合激励下风电机组载荷的低阶线性化控制模型。文献［12］建立了风冰耦合下的塔筒振动模型，并提出了降低风电机组覆冰所致机械载荷的变桨控制策略。文献［13］从理论上分析了湍流强度与风电机组载荷之间的内在联系，并通过仿真计算和样机测试，获取了风电机组在不同强度湍流风运行下的载荷变化规律。上述研究主要关注外部非电扰动所致的风电机组载荷变化，但风电机组是典型机电耦合系统，机组电气运行行为也会影响风电机组的载荷。文献［14］从理论和仿真角度分析了电网故障穿越过程中风电机组出力变化对其机械载荷的影响。文献［15-16］在分析风电机组传动轴机电耦合动态特性基础上，提出了基于电磁转矩附加控制的风电机组传动轴载荷抑制策略。文献［17］指出，发电机短路时风电机组电磁转矩瞬时变化会导致风电机组传动轴产生显著冲击载荷。虚拟惯量控制通过附加与系统频率相关控制环节，使机组具备响应系统频率变化的能力，但虚拟惯量控制构架了机组和电网的机电耦合新通道，其在响应电网频率变化时会改变机组电气运行行为，进而影响机组载荷特性。但是虚拟惯量控制对风电机组机械载荷的影响机理和规律尚不明确。

基于此，以采用直驱永磁同步发电机（directdriven permanent magnet synchronous generator，DPMSG）这一风电主流机型为研究对象，开展虚拟惯量控制对风电机组载荷影响的机理分析和仿真评估研究。首先，在建立虚拟惯量控制下D-PMSG 线性化多体动力学模型基础上，分析虚拟惯量控制对DPMSG 机械载荷影响机理。然后，考虑虚拟惯量控制下D-PMSG 机电相互作用，构建涵盖永磁同步电机及其控制、电网、机械和气动特性等的D-PMSG非线性机电耦合模型。最后，针对电网侧频率扰动和机组侧风速扰动两种运行工况，通过所建非线性机电耦合模型，开展虚拟惯量控制对D-PMSG 机械载荷影响的仿真分析和量化评估研究。

1 虚拟惯量控制对D-PMSG 载荷影响机理

1.1 D-PMSG 虚拟惯量控制

变速恒频风电机组通常采用变流器控制实现最大功率跟踪。但是，电力电子变流器在实现最大功率快速跟踪控制的同时，致使机组转速和系统频率解耦，机组对系统几乎无惯量贡献。为实现DPMSG 对系统的惯量支撑，通常在其变流器控制中引入与系统频率相关控制环节。该控制环节根据系统频率变化率给出相应有功增量参考值PIR。

式中:HIR为虚拟惯量时间常数，通常取值为风电机组的实际惯量时间常数（5 s 左右）；f为系统频率。

加入虚拟惯量控制后，D-PMSG 的总有功功率参考值Pref可用式（2）表示。

式中:Popt为风电机组最大功率点跟踪（maximum power point tracking，MPPT）控制环节给出的最优有功功率参考值。

根据式（2），可得D-PMSG 的典型虚拟惯量控制原理框图如图1 所示。其中，机组总有功功率参考值Pref作为永磁同步电机控制系统的给定值，由机侧或网侧变流器控制电机输出相应有功功率。当系统频率恒定时，机组运行于MPPT 控制模式，总有功功率参考值Pref即为最优有功功率参考值Popt，其由转速ωr通过MPPT 控制环节给出。当系统频率变化时，频率f经微分、滤波、比例等虚拟惯量控制环节后给出有功增量参考值PIR。此时，Pref为最优有功功率参考值Popt与有功增量参考值PIR之和。因此，通过附加虚拟惯量控制环节，D-PMSG 有功功率即可响应系统频率变化，D-PMSG 具备类似同步发电机的惯量响应外特性。

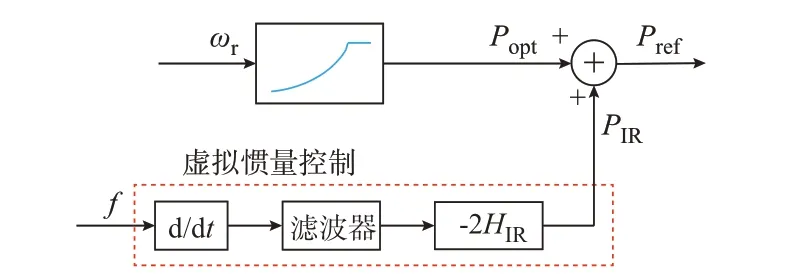
图1 虚拟惯量控制框图Fig.1 Block diagram of virtual inertial control

1.2 载荷影响机理

采用风电机组的线性化多体动力学模型开展虚拟惯量控制对机组载荷影响的机理分析。本文所建线性化模型主要考虑叶片挥舞、叶片摆振、塔筒前后运动、塔筒侧向运动及风轮旋转等几个关键运动模态，如图2 所示。

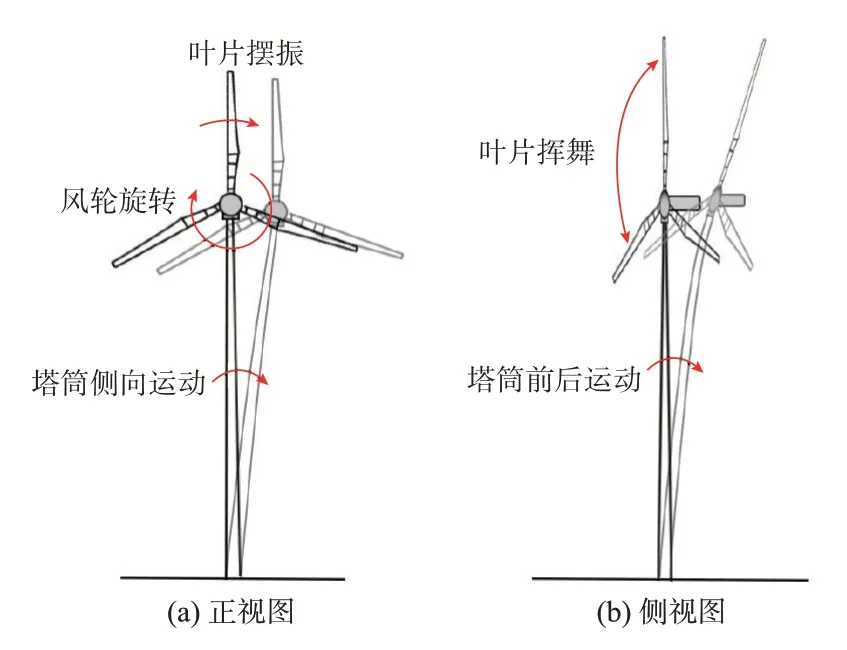
图2 D-PMSG 运动模态示意图Fig.2 Schematic diagram of motion modal of D-PMSG

为简化建模过程，做如下假设［18-19］:1）仅考虑各模态一阶振型；2）不计模态之间弱耦合，仅考虑模态之间强耦合相互作用；3）各叶片挥舞模态一致，摆振模态也一致，即3 个叶片等值为整体；4）不计变桨控制对各模态影响，即认为桨距角恒为零。在上述假设条件下，可得矩阵形式的D-PMSG 线性化多体动力学模型方程如式（3）所示，具体推导过程如附录A 式（A1）—式（A8）所示。

式中:M为质量矩阵；K为刚度矩阵；C为阻尼矩阵；Δq为叶片和塔筒的位移或旋转角度小信号增量矩阵；Δq˙为叶片和塔筒的速度小信号增量矩阵；Δq¨ 为叶片和塔筒的加速度小信号增量矩阵；Δωr为风轮转速小信号增量矩阵；ΔTe为电磁转矩小信号增量矩阵；Δv为风速小信号增量矩阵；γ为转速扰动系数矩阵；η为电磁转矩扰动系数矩阵；λ为风速扰动系数矩阵。上述各矩阵的具体元素见附录A 式（A9）—式（A20）。

无虚拟惯量控制时，认为发电机电磁转矩Te恒定，即式（3）中ΔTe=0，同时考虑式（3）中Δωr=Δq˙，则将右边γΔωr项移至等号左边，可得无虚拟惯量控制的风电机组线性化多体动力学模型方程，如式（4）所示。

式中:C′为阻尼矩阵，如式（5）所示。除C′外，其他矩阵均与式（3）对应矩阵元素完全相同。

式中:C表示阻尼系数，下标b1、b2 分别表示等值叶片挥舞、摆振模态，下标tt、bb 分别表示塔筒、三个叶片的等值阻尼系数，下标t1、t2 分别表示塔筒前后、左右模态，下标r 表示风轮旋转模态，下标“_”表示2 个模态的耦合；γb1、γb2分别为等值叶片挥舞、摆振模态下的转速扰动系数；Fthrust、Taero分别表示风速、风轮转速的非线性函数；μ为塔筒侧向运动受风轮转矩影响的系数。

加入虚拟惯量控制后，系统扰动将引起永磁同步电机电磁转矩Te变化。根据电磁转矩与电磁功率之间关系，式（3）中永磁同步电机电磁转矩Te的小信号增量可用式（7）来表示。

式中:ΔTe，ij为永磁同步电机电磁转矩Te的小信号增量，即电磁转矩小信号增量矩阵ΔTe中的元素；ΔPe为永磁同步电机电磁功率Pe的小信号增量；ωr0、Pe0分别为风轮转速ωr和永磁同步电机电磁功率Pe的稳态运行值；Δωr，ij为风轮转速小信号增量矩阵Δωr中的元素。

忽略永磁同步电机电磁暂态和直流电容动态，即认为输出电磁功率无延迟跟踪功率参考值，则虚拟惯量控制下系统频率变化所致D-PMSG 电磁功率Pe小信号增量表达式为:

式中:Δfij为系统频率f的小信号增量，即系统频率小信号增量矩阵Δf中的元素。

结合式（3）、式（5）和式（8），可得虚拟惯量控制下D-PMSG 线性化多体动力学模型方程，如式（9）所示。

式中:α为频率扰动系数矩阵；C′为改进后的阻尼矩阵。

对比式（4）和式（9），式（9）右边增加了αdΔf/dt扰动项，式（9）等号左边阻尼矩阵C′较式（4）等号左边C′中第4 行第5 列和第5 行第5 列的元素分别增加μPe0/和Pe0/。一般情况下，塔筒和传动轴的固有阻尼远大于μPe0/和Pe0/。因此，可忽略虚拟惯量控制下系统阻尼的变化，主要从αdΔf/dt扰动项角度分析虚拟惯量控制对风电机组机械载荷的影响机理。电网侧频率扰动和风电机组侧风速扰动均直接或间接产生αdΔf/dt扰动项，但虚拟惯量控制下2 种扰动源对机组载荷的影响机制不同，具体分析如下:

1）电网侧频率扰动对载荷影响。电网侧频率包括快变化波动（几秒内）和慢变化波动（10 s 至几分钟）两类，其中，风电机组虚拟惯量控制主要响应电网频率快变化波动。因此，主要分析其对风电机组载荷的影响。此时，可假设风速恒定，即认为式（9）中λΔv=0。式（9）频率扰动系数矩阵α中，与风轮旋转和塔筒侧向模态对应的元素分别为-2μHIR/ωr0，其余元素均为零，表明αdΔf/dt扰动项主要影响风轮旋转模态（对应矩阵方程第5 行）和塔筒侧向模态（对应矩阵方程第4 行）。即虚拟惯量控制下电网侧频率突变可导致塔筒侧向和传动轴模态的自由振动，从而使得塔底侧向和传动轴出现冲击载荷。此外，频率扰动系数矩阵α中-2HIR/ωr0和-2μHIR/ωr0元素的数值大小与虚拟惯量时间常数HIR成正比，且考虑机械系统的非线性特性，表明传动轴和塔底侧向冲击载荷与HIR呈正相关关系。

2）机组侧风速扰动对载荷影响。忽略极端运行阵风、极端风切变等极端风况，仅考虑正常湍流风扰动下风电机组的动态疲劳载荷。正常湍流风扰动会造成频率持续波动，使得虚拟惯量控制下风电机组运行于湍流风况，式（9）除存在λΔv扰动项外，亦存在αdΔf/dt扰动项，即总扰动为λΔv+αdΔf/dt，其与风轮旋转和塔筒侧向模态对应元素的绝对值分别为其中，λa为风轮气动转矩对风速的偏导数。此外，忽略系统延迟，则可认为湍流风变化趋势与系统频率变化趋势相同，即Δvij与dΔfij/dt同正或同负，而μλa、λa、2μHIR/ωr0和2HIR/ωr0符号相同且均为正。

由此可得:

式中:μλaΔvij为式（4）中与风轮旋转模态对应的扰动元素；λaΔvij为式（4）中与塔筒侧向模态对应的扰动元素。上述两不等式表明，相比于无虚拟惯量控制，加入虚拟惯量控制后，作用于传动轴和塔筒侧向的总扰动减小。进一步表明，由扰动引起的塔底侧向和传动轴动态疲劳载荷亦将减小。

2 D-PMSG 机电耦合建模

由上述理论分析可知，借助虚拟惯量控制这一“桥梁”，传统MPPT 控制下机组转速和系统频率的解耦关系被打破，系统机电动态和D-PMSG 机电动态耦合加强。因此，为了研究虚拟惯量控制下DPMSG 机械载荷特性，需要建立兼顾电网和机组机电动态的机电耦合模型。

FAST 软件由美国国家能源实验室开发，具有强大的风电机组载荷计算功能［19］。同时，MATLAB/Simulink 中电气和控制系统工具箱为风电机组电气系统建模和控制算法实现提供了便利，且FAST 与其具有良好接口。因此，采用FAST 和MATLAB/Simulink 联合建模的方法构建并网DPMSG 机电耦合模型，其结构如图3 所示。其中，空气动力和柔性机械结构采用FAST 建模，MATLAB/Simulink 用于构建电网、永磁同步电机及其控制、变桨控制和虚拟惯量控制等电气系统模型。图中:β为桨距角。

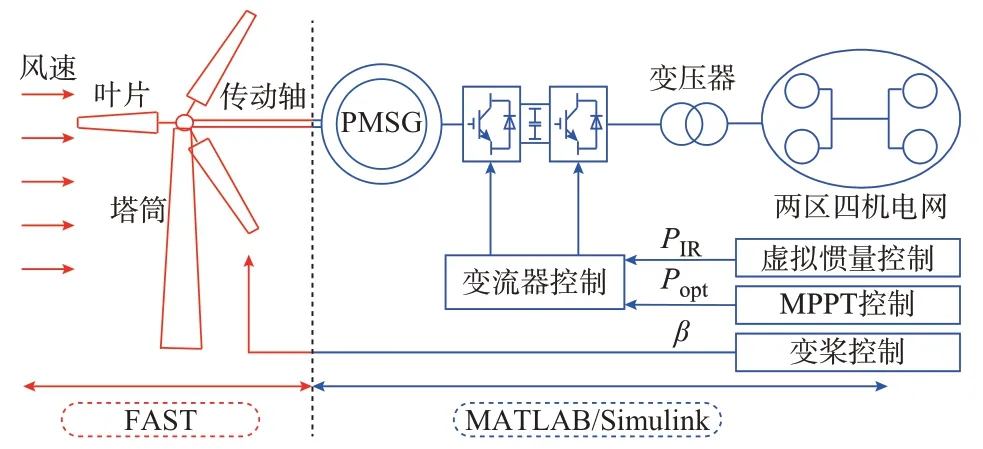
图3 并网D-PMSG 机电耦合模型示意图Fig.3 Schematic diagram of electromechanical coupling model for grid-connected D-PMSG

2.1 空气动力和机械结构模型

在FAST 中，叶片和塔筒视为连接到转子轮毂或地面的悬臂梁，采用假设模态的方法来描述叶片和塔筒的动力学模型。本文将叶片和塔筒分为20 段，每段叶片和塔筒的参数非线性分布。因此，每段叶片和塔筒质量、摆振刚度及挥舞幅度均不同。同时，为了计算的快速性，忽略高阶模态振型。叶片或塔架上某点的弯曲度u(z，t)可用式（12）表示［18-19］。

式中:z为叶片或塔架的中心线；t为时间；φi(z)为叶片或塔架的模态振型，本文只考虑一阶和二阶模态；qi(t)为塔顶或叶尖的空间位置。

传动系统采用两质量块模型表征，其中，风轮整体等效为一个质量块，发电机转子等效为另一质量块，两质量块通过柔性传动轴相连。传动轴扭矩方程表示如式（13）［19-20］所示。

式中:Tshaft为传动轴在发电机端口处的扭矩；Kd为传动轴等效刚度系数；Cd为传动轴等效阻尼系数；θr、θg分别为风力机和发电机位置角；ωg为发电机转速。一般情况下，由于D-PMSG 无齿轮箱结构，所以其传动轴等效刚度系数较大。

FAST 中风轮叶片空气动力模型由AeroDyn 子程序采用叶素动量理论和广义动态入流理论生成。首先，FAST 调用AeroDyn 读取风电机组和环境状态数据；然后，AeroDyn 计算出叶片气动载荷并传入FAST；接着，FAST 根据AeroDyn 传递数据计算出叶片弯曲度和速度，并送回AeroDyn 中计算叶片攻角；最后，AeroDyn 根据叶片攻角计算出修正后的叶片气动载荷。

2.2 永磁同步电机及其控制模型

永磁同步电机是D-PMSG 机电能量转换核心部件，同步旋转坐标系下其定子电压方程如式（14）所示。

式中:usd、usq分别为永磁同步电机定子电压d轴、q轴分量；isd、isq分别为永磁同步电机定子电流d轴、q轴分量；Lsd、Lsq分别为永磁同步电机定子绕组等效电感d轴、q轴分量；Rs为发电机定子电阻；ψf为永磁体在定子绕组中产生的磁链。

永磁同步电机电磁转矩表达式如式（15）所示。

式中:pn为永磁同步电机的磁极对数。

本文所建模型中，永磁同步电机机侧和网侧变流器均采用典型矢量控制方法。机侧变流器实现有功、无功解耦控制，其控制模型如附录B 图B1 所示。图中:Ps为永磁同步电机输出有功功率实际值；usdref、usqref分别为永磁同步电机定子电压d轴、q轴分量参考值；isdref、isqref分别为永磁同步电机定子电流d轴、q轴分量参考值。网侧变流器主要任务是将直流电逆变为与电网同频、同幅交流电、维持直流母线电压恒定以及根据电网需要调节无功，其控制模型如附录B 图B2 所示。图中:Qref、Qg分别为网侧变流器输出无功功率参考值、实际值；Udcref、Udc分别为直流母线电压参考值、实际值；igd、igq分别为网侧变流器实际输出电流的d轴、q轴分量；igdref、igqref分别为网侧电流d轴、q轴分量参考值；ugdref、ugqref分别为网侧变流器并网点电压d轴、q轴分量参考值；Rg为滤波电抗器电阻；Lgd、Lgq分别为滤波电抗器电感d轴、q轴分量；ωd为电网同步角速度。

2.3 功率控制和变桨控制

所建机电耦合模型考虑了D-PMSG 的功率控制和桨距角控制，但不考虑偏航控制。功率控制以转速查表给出功率参考值的方式实现，其控制曲线如附录B 图B3 所示。当系统处于恒功率运行状态时，通过控制桨距角使输出功率稳定在额定功率PN，所采用变桨控制策略如附录B 图B4 所示。给定转速ωref与实际转速ωr之差输入比例-积分（proportional-integral，PI）控制器，从而输出参考桨距角βref，并经限幅、限速环节后送入变桨执行器执行并输出桨距角β。

2.4 电网模型

电网采用接入风电场的经典两区四机系统模型，如附录B 图B5 所示。其中，风电场（wind farm，WF）采用D-PMSG 单机等值模型，接入母线5。4 台同步发电机（synchronous generator，SG）均采用次暂态模型，每台同步电机均投入励磁系统如附录B图B6 所示。每台同步电机的调速系统如附录B 图B7 所示，同步电机及其励磁和调速系统的参数介绍详见文献［21］。两个区域所接负荷L1、L2均采用恒功率等值负荷模型。传输线1 和2 均采用分布参数π 型等值线路模型。

3 电网侧频率扰动对冲击载荷影响的评估

为验证1.2 节虚拟惯量控制下电网侧频率扰动对D-PMSG 冲击载荷影响理论分析的正确性，并量化评估其对冲击载荷的影响，采用所建立的非线性机电耦合模型，选用恒风速电网侧频率突变工况，开展虚拟惯量控制下D-PMSG 冲击载荷仿真分析。其中，同步电机的额定容量设为900 MW，负荷L1、L2均为1 700 MW，传输线1 和2 长度均为100 km，线路等效电阻rl=0.052 9 Ω/km、等效电感xl=1.4 mH/km、等效电容xc=8.82 nF/km，风电场WF由172×5 MW 的D-PMSG 组成，机组主要结构参数见附录B 表B1。仿真工况如下:采用9.5 m/s 恒风速，300 s 时在母线8 投入350 MW 有功负荷用于模拟电网侧频率突变。虚拟惯量控制中惯量时间常数设为4 s。

有/无虚拟惯量控制的系统频率和机组输出有功功率分别如附录B 图B8 和图B9 所示。由附录B图B8 可见，负荷投入后，相较无虚拟惯量控制，风电机组加入虚拟惯量控制后系统频率最低点有所抬升。这是由于电网侧频率突变时，虚拟惯量控制下D-PMSG 快速释放部分动能，使得输出有功功率瞬时增加约0.1 p.u.，而无虚拟惯量控制的机组无法响应系统频率变化。因此，其有功功率无明显变化，如附录B 图B9 所示。

有/无虚拟惯量控制两种情况下D-PMSG 几个关键载荷对比曲线如图4 所示。由图4 可见，电网侧频率突变时，相比无虚拟惯量控制，加入虚拟惯量控制的D-PMSG 传动轴扭矩瞬时增大至3 750 kN·m，较其稳态值增大了约46%。塔底侧向出现了大幅自由振动，振动载荷最大值达4 308 kN·m，较其稳态值增大了约43%。无论加入虚拟惯量控制与否，电网侧频率突变前后D-PMSG 塔底前后方向载荷和叶片弯矩均无显著变化。

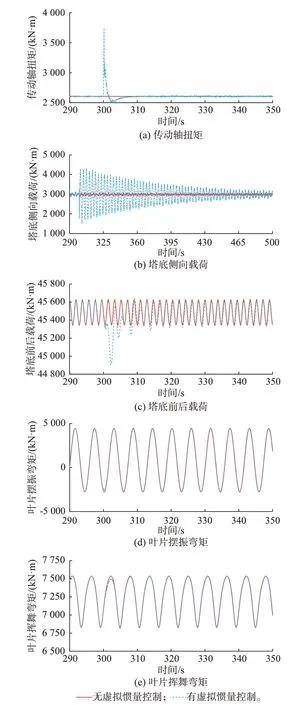
图4 电网侧频率突变时风电机组关键载荷Fig.4 Key loadings of wind turbine when grid-side frequency changes suddenly

此外，为进一步量化评估虚拟惯量控制对机组冲击载荷的影响，在该工况下进一步开展不同虚拟惯量时间常数下机组冲击载荷仿真分析。仿真中，虚拟惯量时间常数分别采用1.0、2.5、4.0 s，并采用冲击载荷最大值、最大变化幅度百分比（即最大变化幅度相对稳态值的百分比）指标对结果进行量化。由于D-PMSG 无齿轮箱结构，其传动轴机械强度设计裕度通常较大，仅给出塔底侧向载荷的量化评估结果，如表1 所示。可见，电网侧频率突变时塔底侧向冲击载荷的最大值和最大变化幅度百分比随着虚拟惯量时间常数的增大而增大。

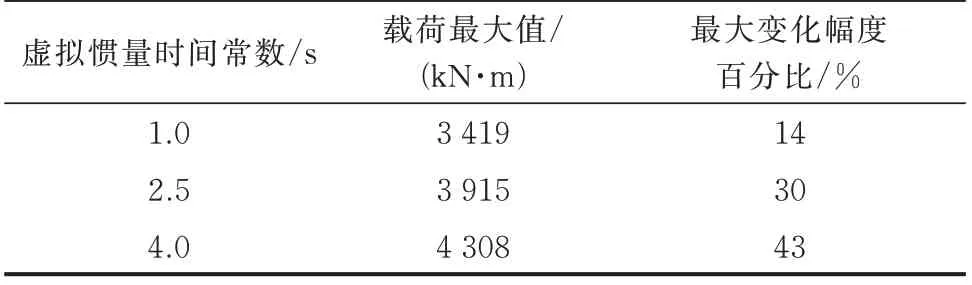
表1 不同虚拟惯量时间常数下塔底侧向载荷评估结果Table 1 Evaluation results of tower bottom lateral directional load under different virtual inertial time constants

除本文1.1 节所述典型虚拟惯量控制方法外，也有较多学者对方波式虚拟惯量控制等方法进行了研究。为增强本文结论的普适性，进一步开展了文献［22］所述方波式虚拟惯量控制与本文所述典型虚拟惯量控制方法，两种不同控制方法下风电机组载荷特性仿真研究。仿真工况如下:采用9.5 m/s 恒风速，300 s 时在母线8 投入350 MW 有功负荷用于模拟电网侧频率突变。虚拟惯量控制中惯量时间常数设为4 s，仿真对比结果如附录B 图B10 所示。结果显示，电网侧频率突变时，两种不同虚拟惯量控制方法下机组输出有功功率、系统频率和风电机组关键载荷均无明显差别。

上述结果表明，电网侧频率突变时，虚拟惯量控制会使得传动轴和塔底侧向出现显著冲击载荷，且其大小与虚拟惯量时间常数呈正相关关系。仿真结果验证了1.2 节电网侧频率扰动对载荷影响理论分析的正确性。

4 机组侧风速扰动对动态疲劳载荷影响的评估

为验证1.2 节虚拟惯量控制下风速扰动对DPMSG 动态疲劳载荷影响理论分析的正确性，并量化评估其对动态疲劳载荷的影响，采用所建非线性机电耦合模型开展典型虚拟惯量控制下D-PMSG载荷仿真，模型中电网参数及D-PMSG 参数与第3 章相同。选用附录B 图B11 所示湍流风进行仿真，其风速平均值为9.5 m/s、湍流强度为12%、时长为10 min，虚拟惯量控制中惯量时间常数设为4 s。采用1 Hz 等值疲劳载荷指标对仿真所得动态疲劳载荷进行量化评估，其中，1 Hz 等值疲劳载荷由Goodman 修正的雨流计数法计算得到（S-N 斜率曲线取值为10）［23］。

该工况下有/无虚拟惯量控制时，系统频率和机组输出有功功率对比曲线分别如附录B 图B12 和图B13 所示。由图B12 和图B13 可见，湍流风扰动下，相比无虚拟惯量控制，加入虚拟惯量控制后系统频率、机组输出有功功率波动均有一定程度减小。

有/无虚拟惯量控制时，关键部件的1 Hz 等值疲劳载荷对比如图5 所示，其时域载荷曲线如附录B 图B14 所示。相比无虚拟惯量控制，加入虚拟惯量控制后机组传动轴1 Hz 等值疲劳载荷由1 110 kN·m 减小至1 060 kN·m，减小约4.5%，塔筒侧向1 Hz 等值疲劳载荷减小约1.5%（如图5 所示）。而无论加入虚拟惯量控制与否，塔底前后和叶片的1 Hz 等值疲劳载荷均无明显差别。

上述结果表明，湍流风扰动下，虚拟惯量控制可以降低D-PMSG 塔底侧向和传动轴的动态疲劳载荷。仿真结果验证了1.2 节机组侧风速扰动对载荷影响理论分析的正确性。