新型可变可控三油楔轴承结构设计及静态特性分析
2024-04-17凡丰成郭红石明辉陈书杰
凡丰成,郭红,石明辉,陈书杰
(郑州大学机械与动力工程学院,河南郑州 450001)
随着高速机械装备的广泛应用,对滑动轴承的性能提出了越来越高的要求。传统的被动式滑动轴承[1-4]在面对变工况条件时,会存在一定的局限性,不能根据实际工况调节轴承参数,由此可能会造成轴承的磨损,缩短轴承的使用寿命。因此开展轴承参数主动调控的研究具有重要的意义。
关于可变可控轴承的研究,学者们通过理论和实验研究取得了一系列的成果,很多具有主动可控的轴承被提出来,比如磁悬浮轴承、可控液压轴承和主动可倾瓦轴承等。刘旭辉等[5]设计了一种新型铁磁流体滑动轴承,搭建了磁流体轴承的测试平台,分析了该磁流体轴承在不同电流下的振动情况,研究结果表明磁流体轴承可以抑制转子的振动。秦鑫等人[6]开展了主动控制可倾瓦轴承-转子系统动态性能理论仿真研究,在控制不同可倾瓦径向位移及周向角度的情况下分析了轴承的静动态性能及轴心轨迹。理论研究结果表明,增加对轴瓦径向位移和周向角度的控制量可以有效减小转子轴颈振幅,提高轴承-转子系统的运行稳定性。吴超等人[7]提出了一种新型线切割一体化径向滑动轴承,建立了该新型轴承的数学模型,考虑支座变形和瓦块变形的影响,研究了偏心率、轴颈转速和支点几何尺寸对轴承静态性能的影响。张磊等人[8]提出了一种下轴瓦可调的轴承概念,通过FEM数值方法建立了转子-轴承模型,利用该模型研究了可调椭圆轴承对转子加速过程中动力学特性的影响,经过理论计算与实验研究验证了合理调节椭圆度可以明显减小转子的振动。
综上所述,目前学者们主要基于电磁、液压或机械系统来控制轴承进而改善轴承性能,但是电磁控制系统复杂、价格昂贵,可控液压和机械系统反馈速度慢、调节精度低。随着时代的发展进步,功能型材料在很多结构之中得到了广泛应用。例如,由压电材料制作而成的压电叠堆作动器具有响应快、精度高的优点已被广泛应用于机械、土木、航空航天结构的主动控制中[9-12]。本文作者提出了利用压电叠堆直接作用于轴瓦上使其变形,得到了一种可变可控三油楔轴承。该轴承通过对压电叠堆施加驱动电压调节油膜间隙来调整轴承的工作状态,因压电叠堆响应速度快、控制精准,因此这种轴承具有调节速度快且具备主动控制能力的特点。
由压电叠堆控制形成的可变可控三油楔轴承的性能不仅与传统轴承的参数有关,还和驱动电压的大小有关。本文作者采用CREO软件建立了油膜的几何模型并导入前处理软件ICEM中进行结构化网格划分,基于FLUENT软件中的两相流模型计算分析了电压、偏心距及转速对轴承静态性能的影响。
1 可变可控三油楔轴承结构设计及工作原理
1.1 新型轴承结构设计
基于压电叠堆的结构特征,将其嵌入轴承结构之中,对压电叠堆施加直流驱动电压后,压电叠堆会产生拉伸变形促使轴承结构发生变形。图1为可变可控三油楔轴承结构示意图,主要由轴承体、压电叠堆及楔形块组成。在轴承圆周方向特别设计了均匀分布的凹槽,在每个凹槽内安装了一个压电叠堆,通过楔形块对其进行固定。
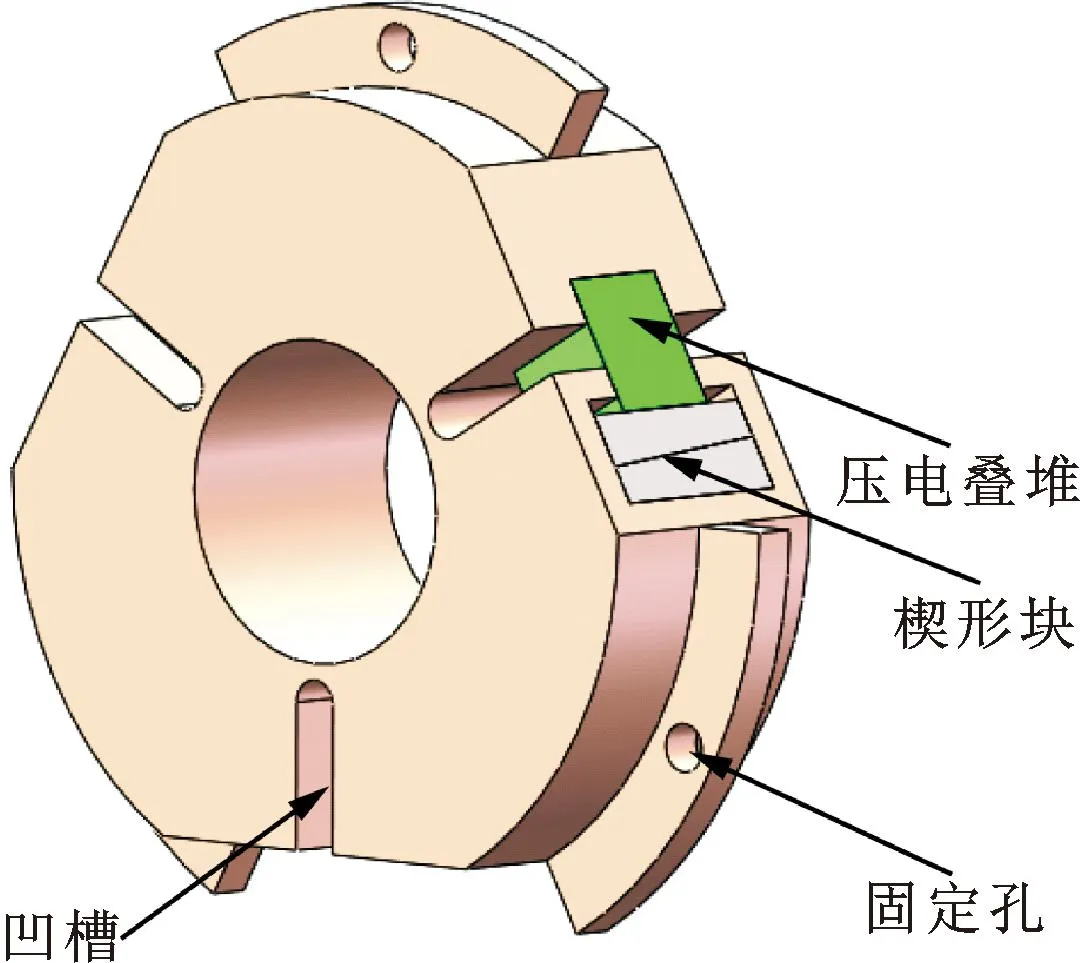
图1 可变可控三油楔轴承结构示意
1.2 新型轴承工作原理
当对压电叠堆施加直流驱动电压时,压电叠堆产生的静态力使轴承产生一定的静态变形,由于凹槽的存在,轴承内壁由圆形变成三油楔形状,内壁变形示意图如图2所示。传统的三油楔轴承有三块均布的相同轴瓦,每块轴瓦对应不同的圆心,相邻两块瓦之间均可形成油楔[13-14]。文中提出的可变可控三油楔轴承具有调节油膜间隙的能力,通过改变直流驱动电压的大小可以控制轴承的变形程度,实际运转过程中可以根据相应的工况来选择合适的直流驱动电压。
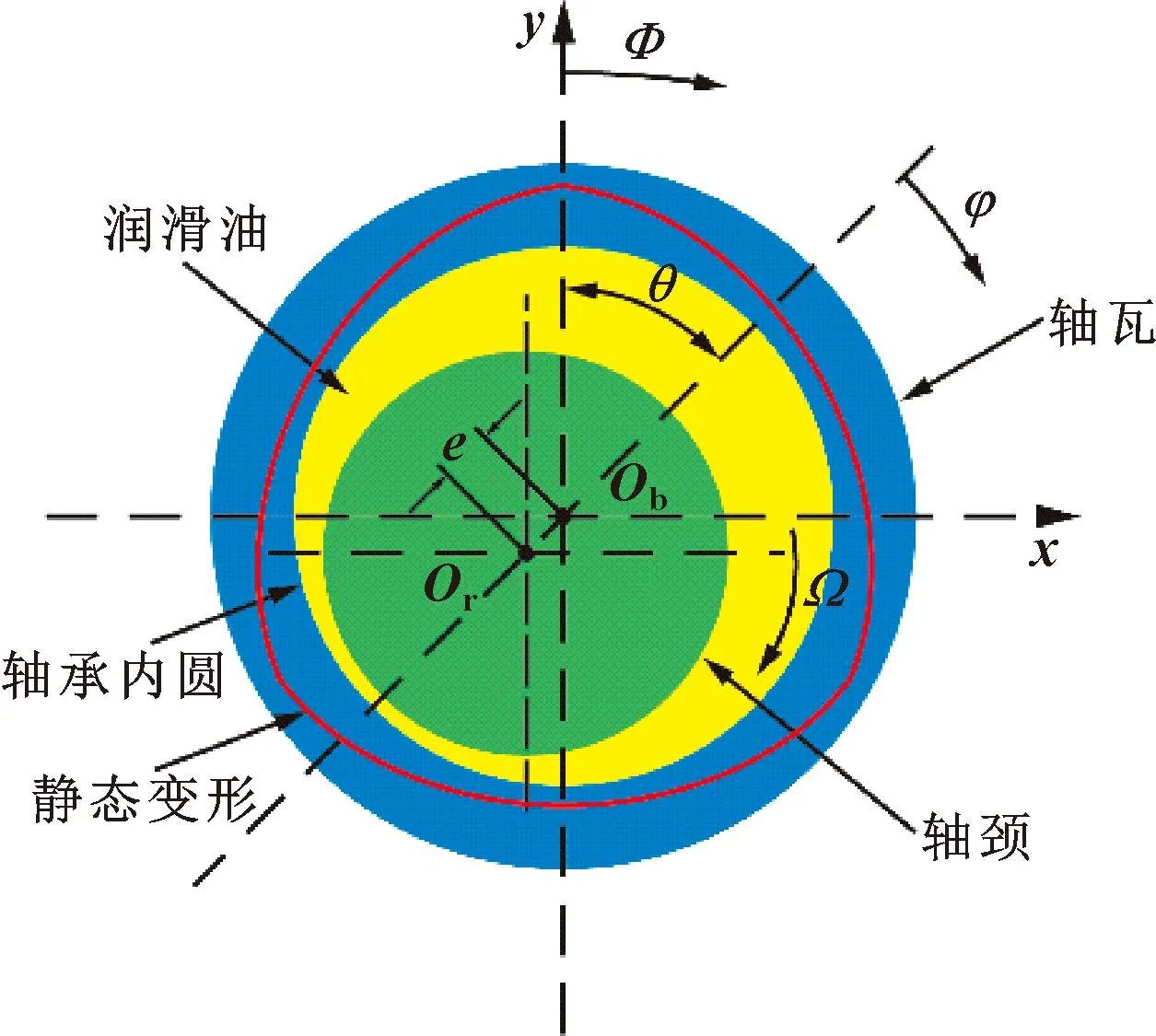
图2 轴承内壁变形示意
2 可变三油楔轴承特性仿真
2.1 轴瓦变形仿真计算
采用有限元仿真软件ANSYS对压电叠堆控制形成的三油楔轴承进行仿真分析。首先,建立静力学分析模块,定义压电叠堆、轴承和楔形块材料;其次,导入模型并将所用材料赋予模型;然后,建立新的局部坐标系并对模型进行网格划分;最后,将固定约束施加在轴承的外缘小孔并给压电叠堆赋予极化方向,输入相关参数进行仿真求解。
2.2 可变三油楔轴承油膜特性方程
随着计算机技术的发展,学者们普遍采用CFD方法直接求解N-S方程研究滑动轴承中的油膜工作情况[15-16]。流体流动受物理守恒定律的支配,包括质量守恒定律、动量守恒定律和能量守恒定律,文中的研究中不涉及能量的变化,因此流体流动仅需遵循质量守恒定律和动量守恒定律。考虑到轴承发散区存在空穴现象,文中选用FLUENT中的Mixture两相流模型,Mixture两相流模型的优点是无需定义油膜破裂的边界。
(1)质量守恒方程
轴承运转过程中其间隙内的流体遵循质量守恒定律,可用质量守恒方程来描述,即
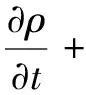
(1)
式中:ρ为气液两相混合密度;t为时间;v为速度矢量;∇为哈密尔顿算子。
(2)动量守恒方程
假设油膜中流体微元体的动量对时间的变化率等于外界作用在该微元体上的各种力之和,其表达式为
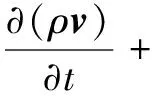
(2)
τ=μ[(∇v+∇vT)-2/3∇·vI]
(3)
式中:p为流体微元体上的压力;F为外部体积力;τ为应力张量;μ为混合相动力黏度;I为单位张量。
2.3 FLUENT仿真模型
可变可控三油楔轴承的结构如图2所示,其中Ob和Or分别为轴承中心和转子中心,e为转子偏心距。在一定偏心距下,轴颈顺时针旋转,润滑油从轴承两端流出。将压电仿真后的轴承内壁提取出来,导入三维建模软件CREO建立油膜三维模型。在ICEM中进行结构化网格划分,为了更加真实地反映润滑油在轴承间隙中的流动情况,需要注意油膜厚度方向上的网格层数,原则就是在保证计算精度的前提下尽可能地降低网格数量,这样既提高了计算效率,又保证了计算结果的可靠性。综合考虑,在油膜厚度方向划分为5层,油膜模型被划分为181 532个六面体网格,油膜网格划分模型如图3所示。
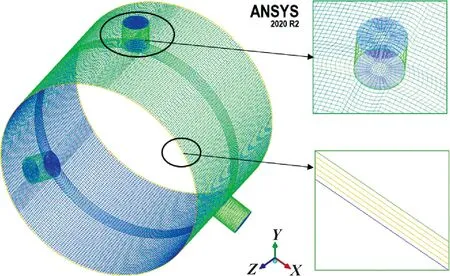
图3 油膜网格模型
2.4 模型假设与求解设置
在进行FLUENT仿真计算时,从宏观流体力学角度对滑动轴承流场开展研究,做出如下假设:
(1)假设润滑油为不可压缩流体且为三维定常流动状态;
(2)润滑油与轴径轴瓦接触无相对滑移;
(3)经过计算得到雷诺数Re<2 300,流动状态为层流;
(4)不考虑轴颈与轴瓦之间的热传导。
FLUENT仿真求解设置如下:
(1)求解模型设置为层流和两相流模型;
(2)设定进油口为压力入口,供油压力为0.2 MPa;设定轴承两端面间隙为压力出口,压力值为大气压力,油膜内表面设定为旋转壁面边界条件,其余表面均设置为固定壁面边界条件;
(3)求解方法为SIMPLEC,混合初始化后进行求解。
2.5 仿真模型验证
为了验证计算方法的正确性,采用文献[17]中相同的轴承结构进行仿真求解并与该文献中的计算结果进行对比。轴承结构参数如表1所示,结果如图4—6所示。可知,采用FLUENT仿真求解得到的静态特性参数与文献[17]中数值求解结果较为吻合,验证了仿真模型的正确性。

表1 轴承结构参数
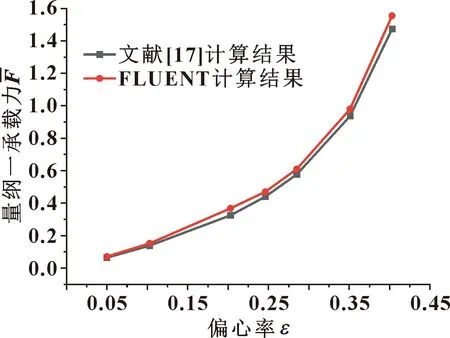
图4 不同偏心率下的量纲一承载力对比

图5 不同偏心率下的量纲一摩擦力对比

图6 不同偏心率下的量纲一端泄流量对比
3 可变可控三油楔轴承计算结果与分析
FLUENT仿真计算采用的轴承及工况参数如表2所示。
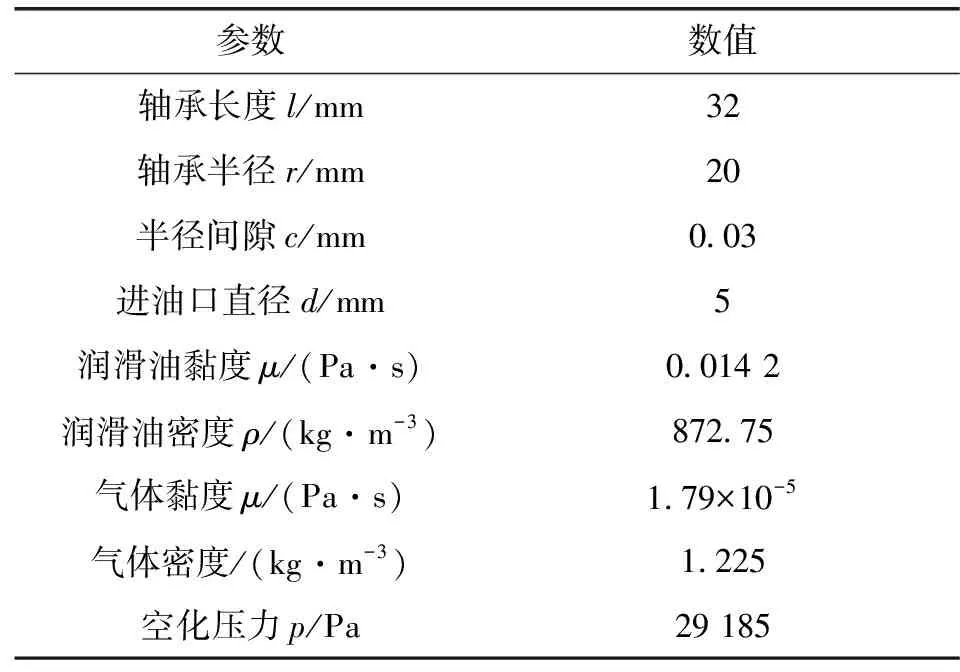
表2 轴承结构及工况参数
3.1 不同电压下的轴瓦变形
图7—9所示分别为90、120、150 V驱动电压下的轴承变形仿真结果,可以看出在施加驱动电压后轴承内表面由圆形变成三油楔形状,驱动电压越高,轴承变形量越大,油膜间隙越大。图10所示为轴承中间截面在90、120、150 V驱动电压下的变形结果,可知随着驱动电压的升高,轴承中间截面的变形量越来越大,轴承结构的特殊设计使其变形量呈现一定的规律性。
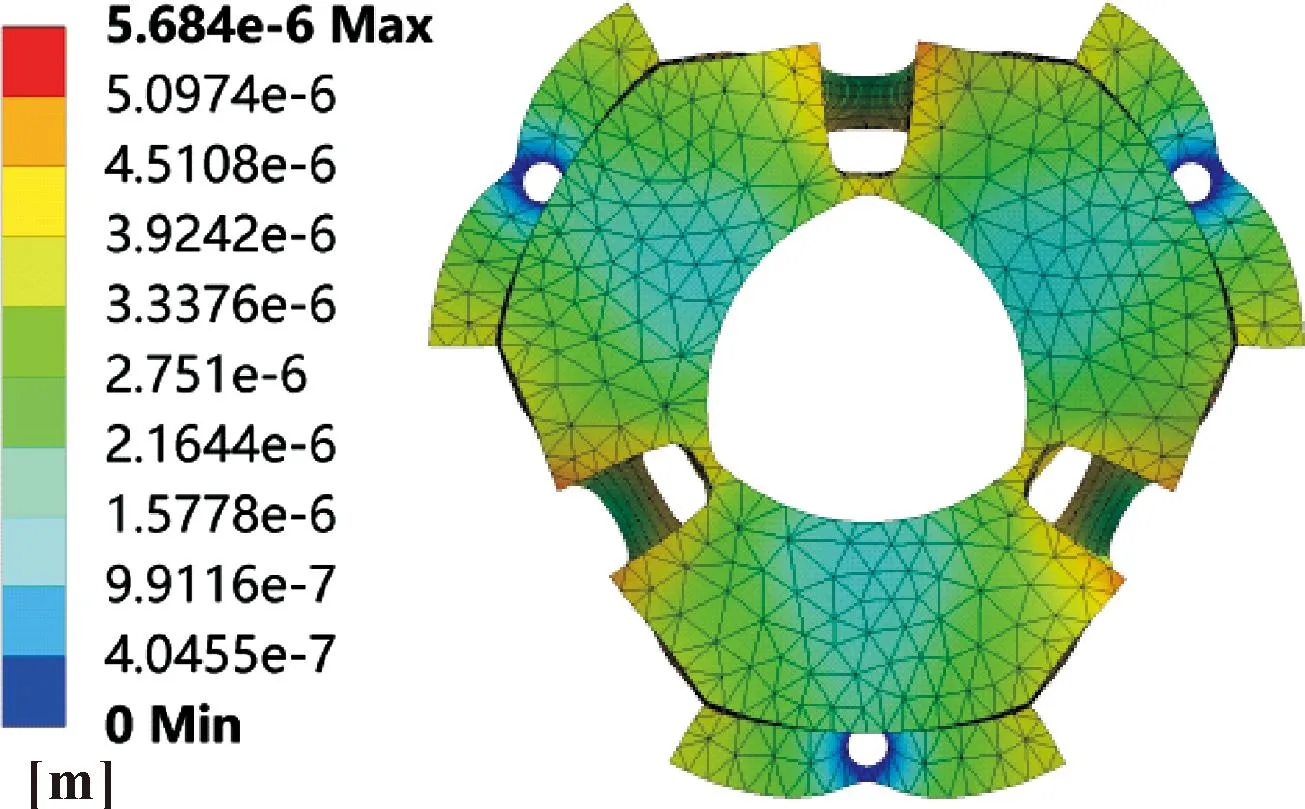
图7 90 V驱动电压下轴承变形
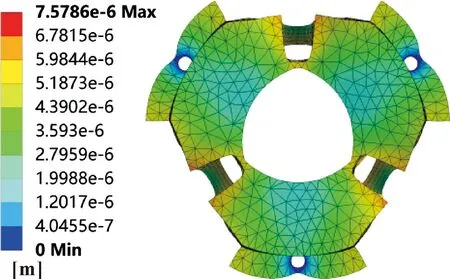
图8 120 V驱动电压下轴承变形
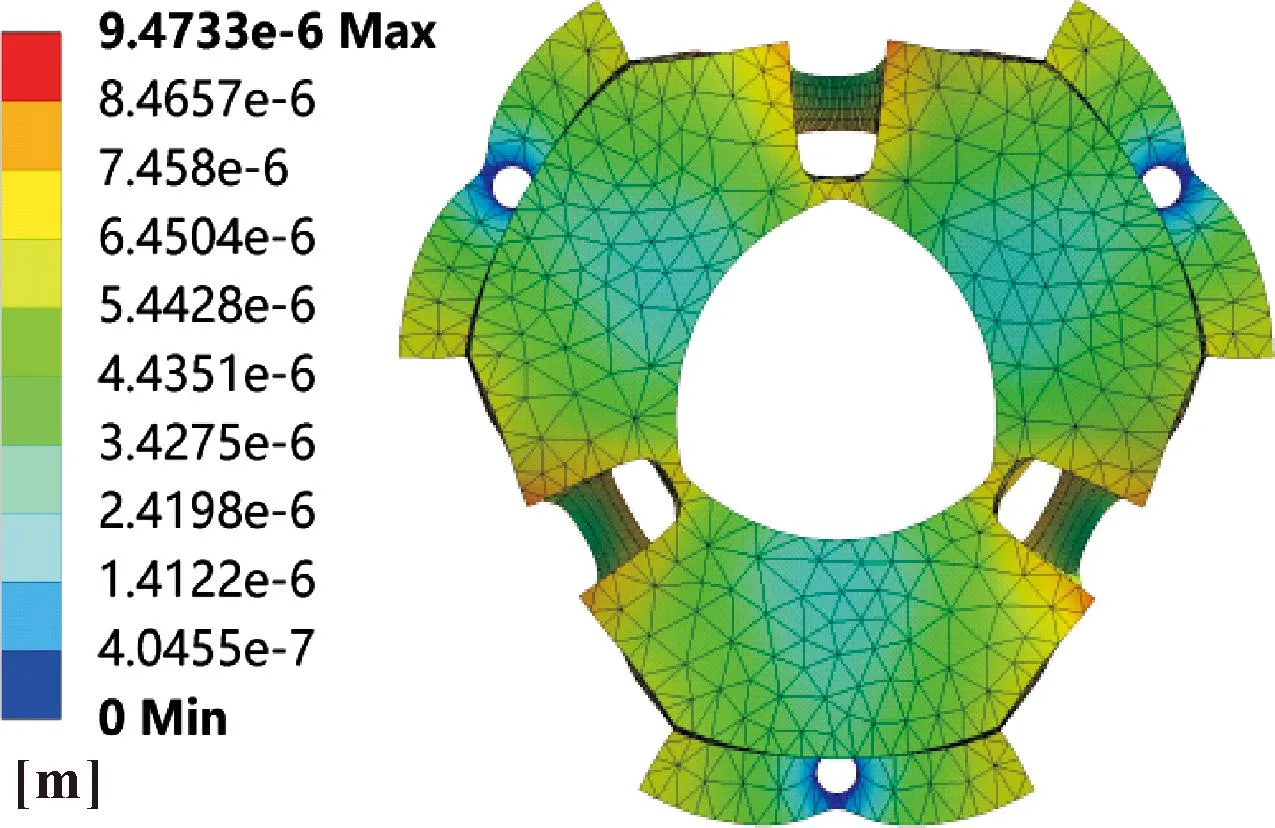
图9 150 V驱动电压下轴承变形
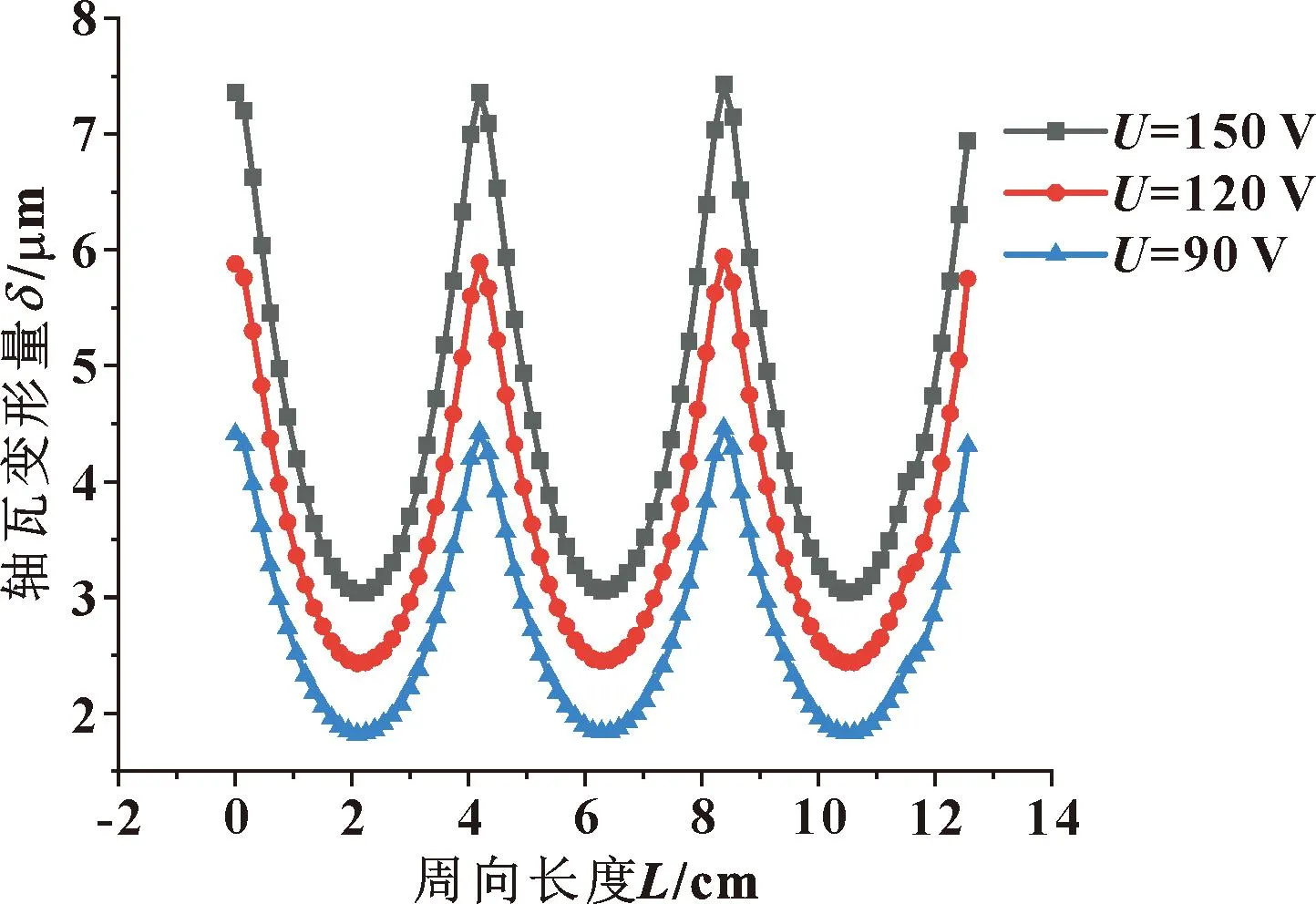
图10 不同驱动电压下轴承中间截面变形
3.2 不同状态下的油膜压力分布
在压电叠堆的控制下,轴承结构发生了变形,轴承变形的程度取决于施加驱动电压的大小,轴承的变形改变了轴承的油膜压力分布,轴承的静态特性也随之改变。
图11—14分别示出了轴承在偏心距e=15 μm时变形前后的油膜压力分布,可知轴承变形前后油膜压力分布发生了明显的变化,最大油膜压力出现在最小油膜厚度附近。

图11 轴承变形前油膜压力分布(U=0,n=3 000 r/min,e=15 μm)

图12 轴承变形后油膜压力分布(U=90 V,n=3 000 r/min,e=15 μm)
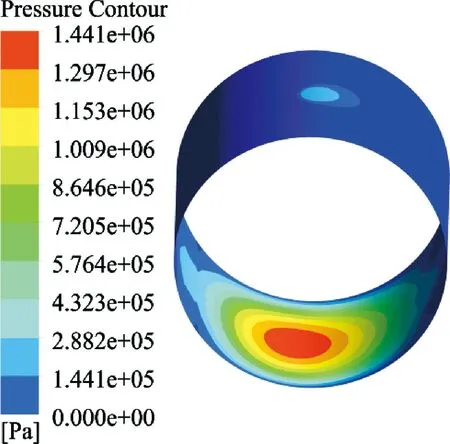
图13 轴承变形后油膜压力分布(U=120 V,n=3 000 r/min,e=15 μm)

图14 轴承变形后油膜压力分布(U=150 V,n=3 000 r/min,e=15 μm)
图15示出了轴承中间截面油膜压力分布,可知随着驱动电压的升高,最大油膜压力逐渐减小。
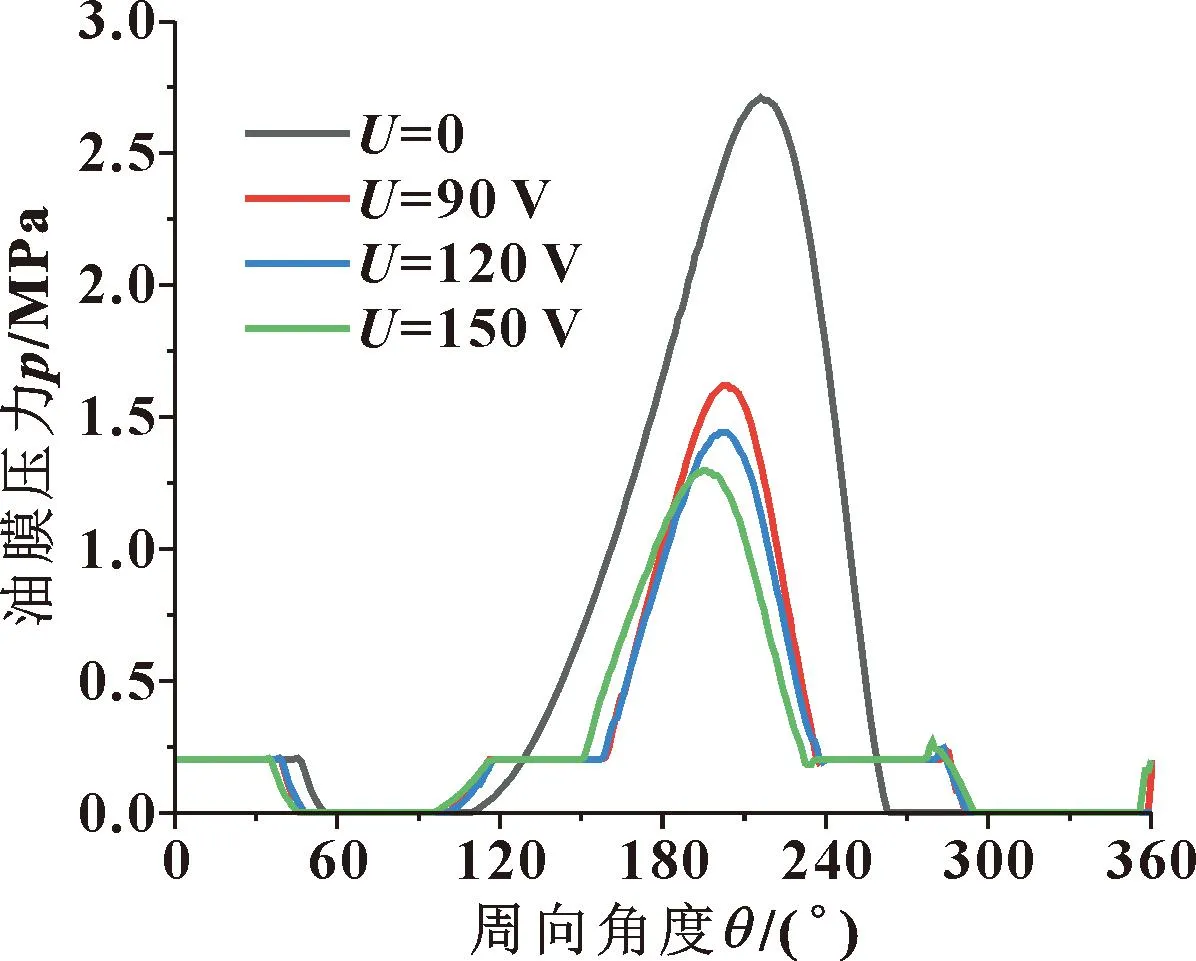
图15 轴承变形前后周向油膜压力分布
3.3 新型轴承静态性能分析
图16(a)示出了不同驱动电压下偏位角随偏心距的变化关系,计算时转速为3 000 r/min。图16(b)示出了不同驱动电压下偏位角随转速的变化关系,计算时偏心距为15 μm。
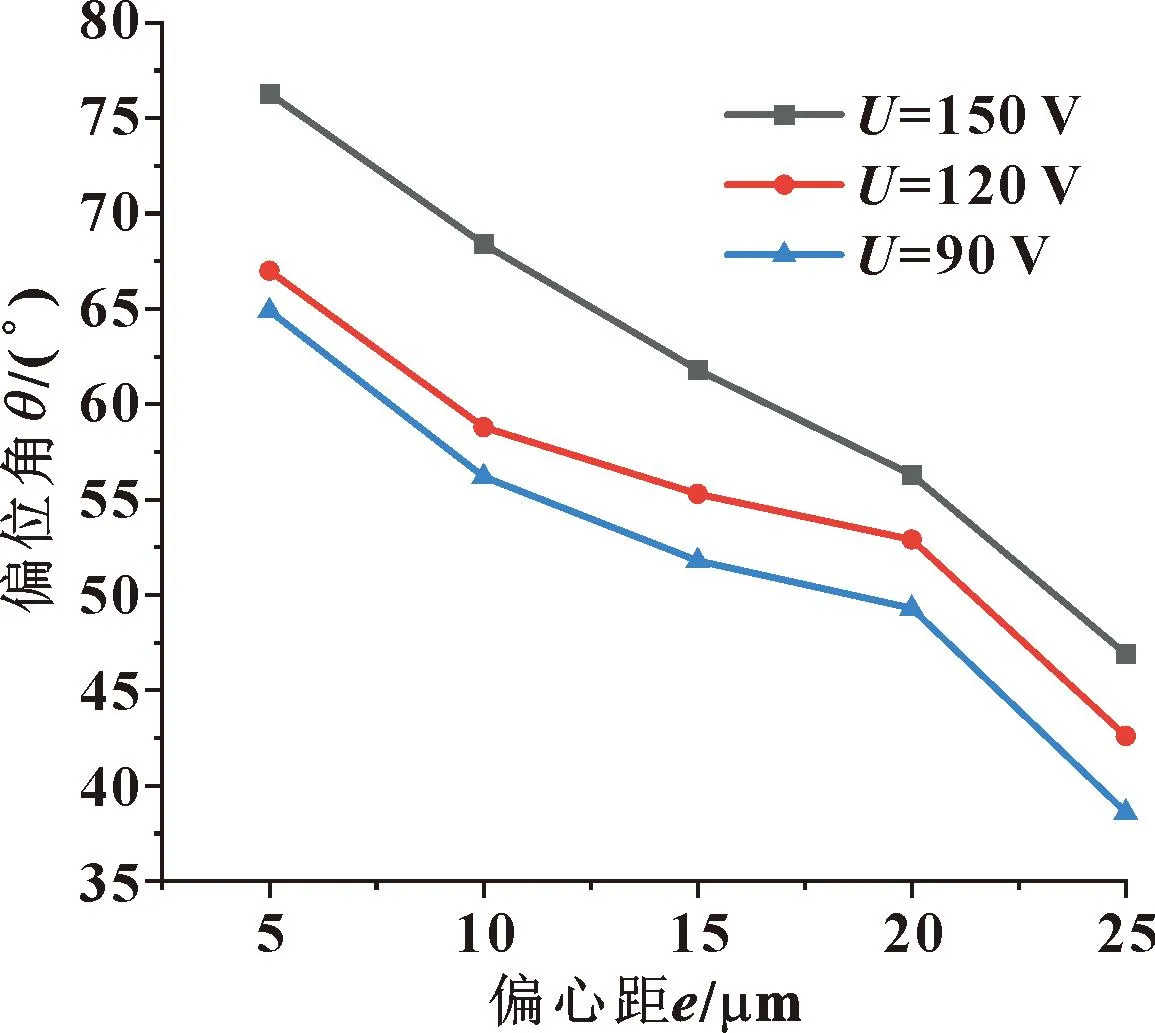
图16(a) 不同电压下偏位角随偏心距变化(n=3 000 r/min)
可知,随着偏心距或转速的增加,偏位角逐渐减小。偏位角的减小主要是由于偏心距和转速增加导致油膜压力逐渐增大造成的。在相同偏心距或转速下,直流驱动电压越高,偏位角越大,主要原因是电压越高,轴承变形越大,油膜间隙的增大引起动压效应减小,油膜压力越小,偏位角越大。
图17(a)示出了不同驱动电压下轴承承载力随偏心距的变化关系,计算时转速为3 000 r/min。图17(b)示出了不同驱动电压下轴承承载力随转速的变化关系,计算时偏心距为15 μm。可知,承载力随偏心距和转速的增大而增大,承载力的增大主要是由于偏心距和转速增加导致动压效应增强造成的。在相同偏心距或转速下,直流驱动电压越高,承载力越小,主要原因是电压越高,轴承变形越大,油膜间隙的增大引起动压效应减小,承载力也越小。

图17(a) 不同电压下承载力随偏心距变化(n=3 000 r/min)
图18(a)示出了不同驱动电压下轴承摩擦力随偏心距的变化关系,计算时转速为3 000 r/min。图18(b)示出了不同驱动电压下轴承摩擦力随转速的变化关系,计算时偏心距为15 μm。可知,摩擦力随偏心距和转速的增大而增大,摩擦力的增大主要是由于偏心距和转速增加导致动压效应增强造成的。在相同偏心距或转速下,直流驱动电压越高,摩擦力越小,主要原因是电压越高,轴承变形越大,油膜间隙的增大引起动压效应减小,摩擦力也越小。

图18(a) 不同电压下摩擦力随偏心距变化(n=3 000 r/min)
图19(a)示出了不同驱动电压下流量随偏心距的变化情况,计算时转速为3 000 r/min。
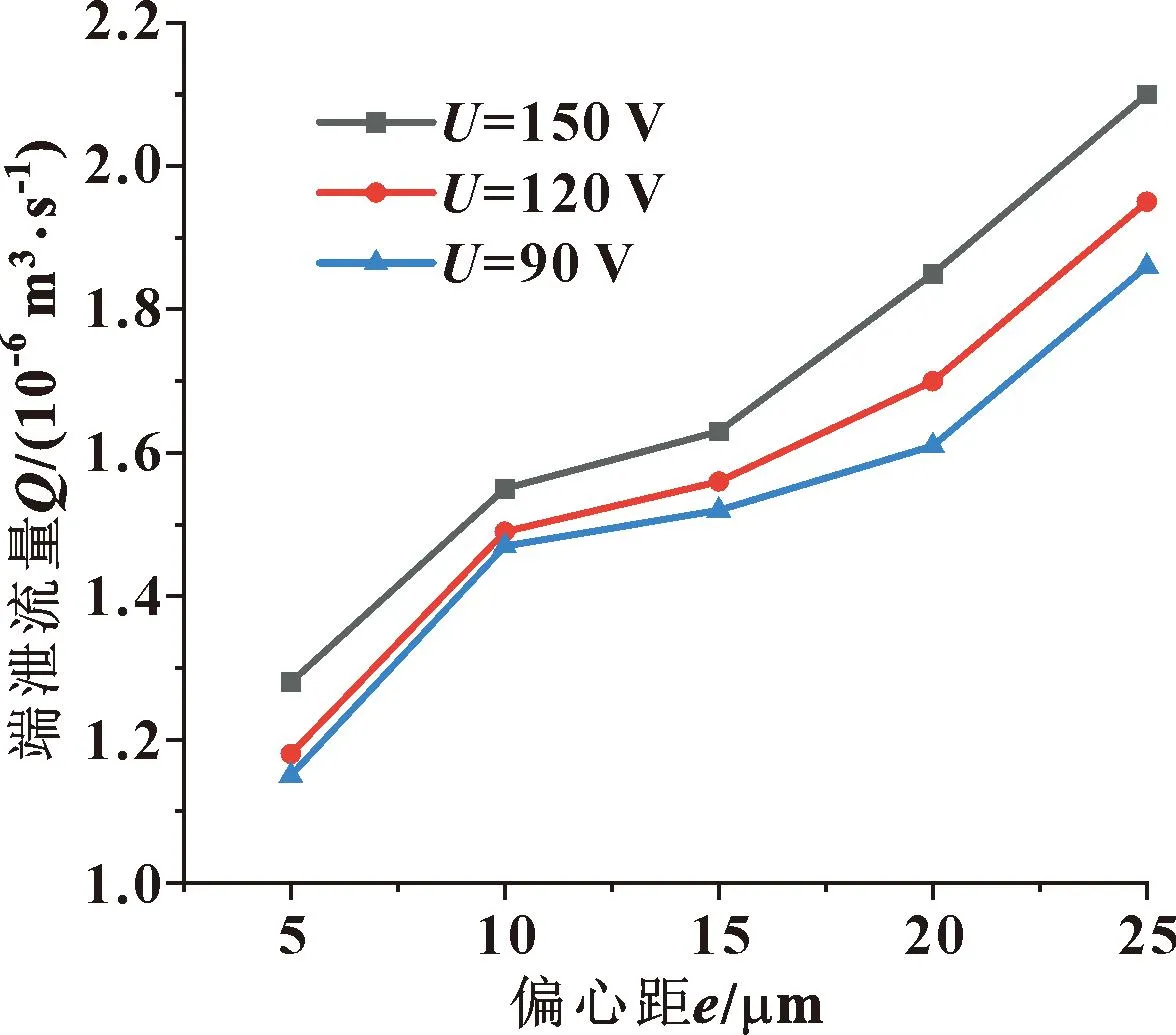
图19(a) 不同电压下端泄流量随偏心距变化(n=3 000 r/min)
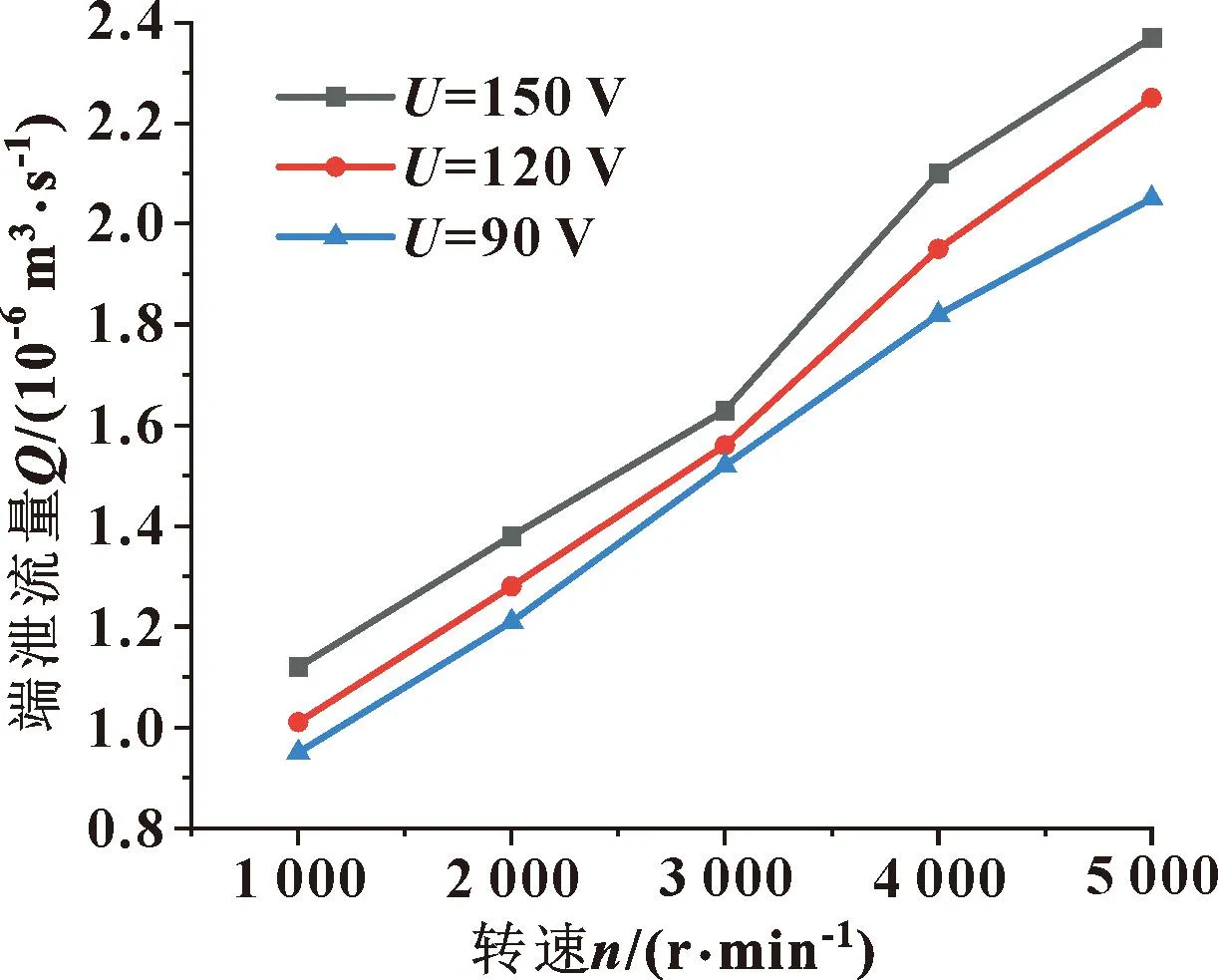
图19(b) 不同电压下端泄流量随转速变化(e=15 μm)
图19(b)示出了不同驱动电压下流量随转速的变化关系,计算时偏心距为15 μm。可知,流量随着偏心距和转速的增大而增大。在相同偏心距或转速下,驱动电压越高,油膜间隙越大,流量随着油膜间隙的增大而增大。
4 结论
(1) 提出了一种可变可控三油楔轴承,采用压电叠堆控制轴承的变形,其具有响应速度快、控制精准的优点。
(2)随着驱动电压的升高,轴承截面的变形量越来越大,油膜压力分布发生明显的变化,最大油膜压力逐渐减小。因此实际运行过程中可以根据不同的工况选择不同的驱动电压,从而控制轴承的变形程度和油膜压力分布。
(3) 由压电叠堆控制引起的轴瓦变形改变了油膜压力分布和轴承静态性能,轴承的承载力、摩擦力和流量均随偏心距和转速的增大而增大;在一定偏心距或转速下,随着驱动电压的升高,承载力和摩擦力逐渐减小,流量逐渐增大。
