试验台约束对滑动轴承动特性识别精度的影响

2024-04-17陈润霖唐杰徐帆杜辰崔亚辉刘凯

润滑与密封 2024年3期

陈润霖，唐杰，徐帆，杜辰，崔亚辉，刘凯

(西安理工大学机械与精密仪器工程学院，陕西西安 710048)

在滑动轴承动特性测试过程中，试验台本身的参数对测试结果会产生一定的影响[14]，采用不同的测试方法，这种影响也各不相同[15]。OUYANG等[16]分析了测量系统误差对轴承动态特性系数识别误差的影响规律，并提出了一种测量系统磁悬浮动态标定方法。DU等[17]分析了试验台磨合期及正常运行期轴颈相对间隙对轴承性能的影响。除此之外，在动特性测试过程中，由于试验台产生的幅值误差和相位误差同样会对轴承动特性系数识别精度产生影响[18]。

本文作者以倒置式轴承动特性试验台为例，基于轴承动力学正反问题，提出考虑测试误差时轴承动特性识别精度仿真评估方法，重点分析试验台约束刚度和约束阻尼的大小对轴承动特性系数识别精度的影响规律，为滑动轴承动特性识别试验台的建设和测试参数选取提供了数据参考。

1 滑动轴承倒置式试验台方案及动特性识别方法

1.1 试验台方案及约束装置

滑动轴承倒置式试验台方案如图1所示，转子由滚动轴承支承，并在驱动力的作用下旋转，试验轴承为滑动轴承，在激振力的作用下可以浮动。为了保证滑动轴承在动特性测试中与转子轴线保持平行，只产生平动而不发生摆动，需要对试验轴承进行合理约束。文中试验台采用链条约束[19]，即将8根链条布置于试验轴承两侧进行运动约束，属于柔性约束。在试验轴承组件上焊接铁钩用于连接链条一端，另一端使用“外螺纹+双螺母”的形式固定于试验台基体上，从而使链条处于拉紧状态，限制试验轴承运动。链条设计及安装如图2所示。

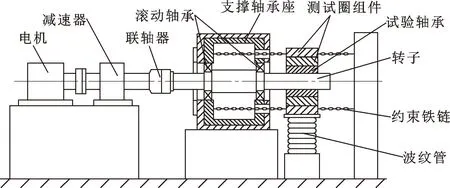
图1 倒置式轴承动特性试验台方案

1.2 动特性识别方法

针对倒置式轴承动特性试验台，其动力学模型如图3所示，以单频两次激振法为例，假设所施加的激振力矢量通过轴承的几何中心，且轴承作平面平行运动，可得到试验台系统的运动微分方程如公式(1)所示。

(1)

式中：F1、F2为激振力；(X，Y)为试验轴承相对于静平衡位置的绝对位移；(X1，Y1)为试验轴承处转子的绝对位移；(X2，Y2)为试验轴承轴孔中心相对转子轴心的位移；m、m1分别为试验轴承和转子质量；k、c分别为试验轴承的刚度和阻尼系数矩阵；k0、c0分别为试验台连接刚度和阻尼系数矩阵；k1、c1分别为转子支撑的刚度和阻尼系数矩阵。

对试验台的运动微分方程进行傅里叶变换，消去X1和Y1，可得方程：

(2)

公式(2)为滑动轴承动特性测试的单频2次激振法的测量方程，代入2次测试得到的激振力、位移数据，可得到8个线性方程，从而求解出滑动轴承的8个动特性系数，完成动特性系数的识别。

2 滑动轴承动特性系数的识别精度仿真评估方法

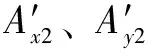
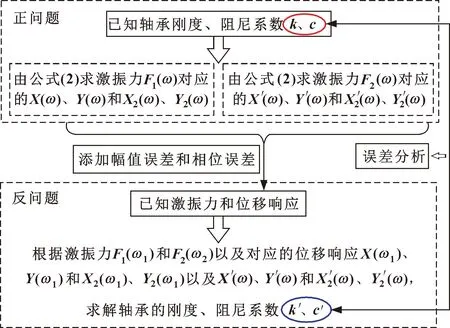
图4 基于轴承动力学正反问题的动特性系数识别精度评估方法

在实际测试过程中，由于测试仪器硬件和环境的干扰，测试获取的信号与真实信号之间存在误差，这种测试误差主要包括幅值误差和相位误差，将测试误差直接添加到仿真得到的位移数据中，用于模拟真实振动测试数据，即：

(3)

式中：Am0、Am为添加误差前后信号的幅值；φ、φ0为添加误差前后信号的相位；aA、aφ分别为幅值的相对误差和相位的绝对误差。

根据动特性识别的求解算法，将添加测试误差的振动信号作为输入，可识别出轴承的刚度、阻尼系数矩阵k′、c′，将其与试验台轴承的刚度、阻尼的设定值k、c进行对比，可评估轴承动特性系数的识别精度为

(4)

式中：εk为刚度系数识别误差；εc为阻尼系数识别误差。

3 试验台约束对轴承动特性系数识别精度的影响分析

3.1 试验台系统的参数

文中所研究的滑动轴承倒置式试验台系统参数如表1所示。对于所采用的测试仪器系统，结合被测轴承的实际情况，经过动态标定以后[20]，测试过程中存在+5%的幅值误差和+1°的相位误差。

表1 倒置式轴承动特性试验台的参数

3.2 约束刚度的影响分析

当试验台约束刚度为表1中初值的0.001～1 000倍时，在激振频率为0～1 000 Hz时试验台约束刚度对轴承动特性系数的影响规律分别如图5、图6所示。为便于分析，将所有图均分别分为5个部分，其中，A部分为低频率和低约束刚度时主刚度识别误差，B部分为低频率和高约束刚度时主刚度识别误差，C部分为转子共振频率附近时主刚度识别误差，D部分为高频率和低约束刚度时主刚度识别误差，E部分为高频率和高约束刚度时主刚度识别误差。

图5 不同约束刚度时轴承主刚度的识别误差

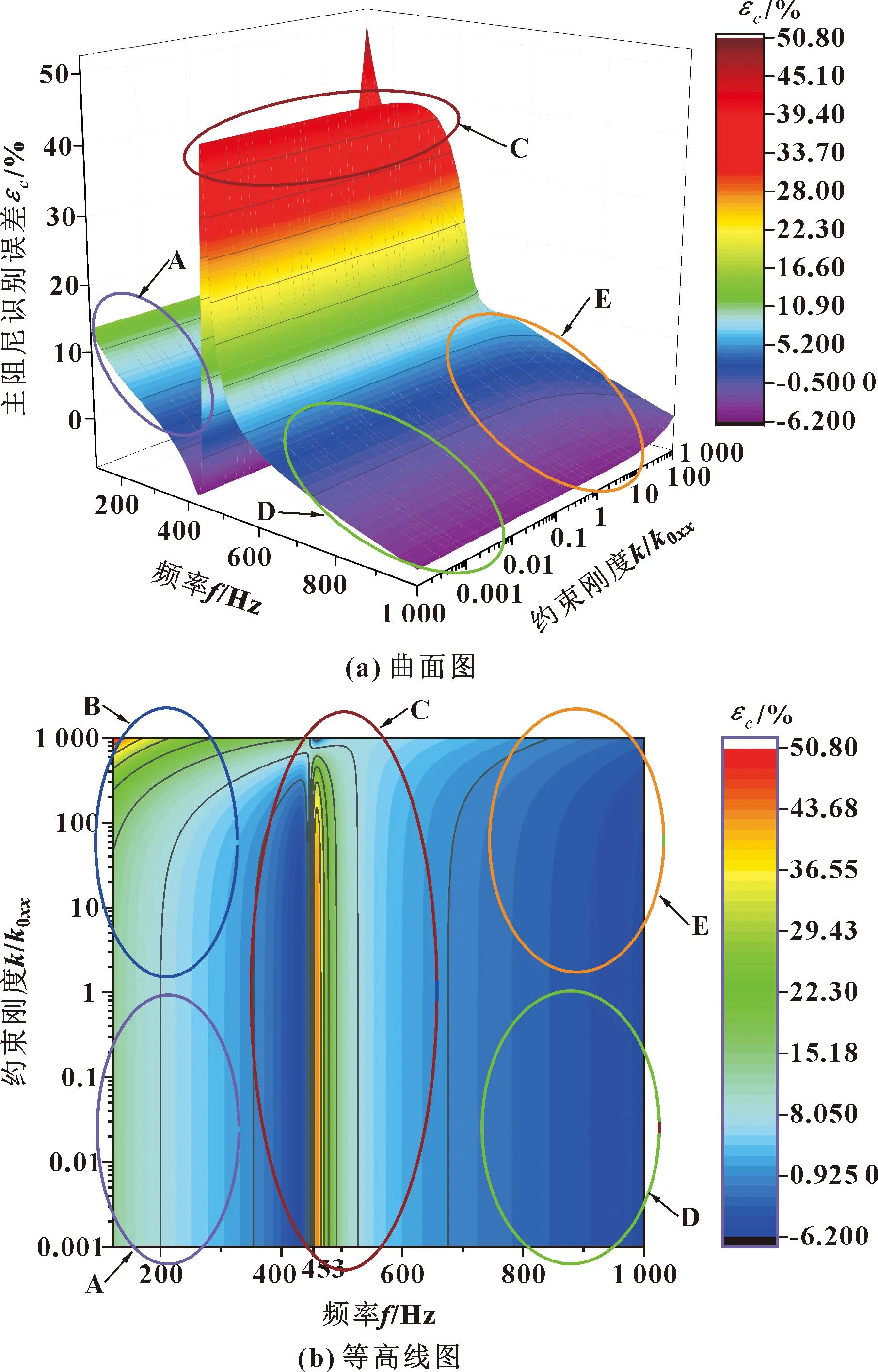
图6 不同约束刚度时轴承主阻尼的识别误差

从图5中可以看出，当激振频率和约束刚度较小时，即在A部分时，轴承主刚度识别误差在0附近，主刚度识别精度较好；在B和E部分，轴承主刚度识别误差均有逐渐增大的趋势，主刚度识别精度次之；在C部分，由于激振频率与转子频率产生共振，所以轴承主刚度识别误差存在较大波动，主刚度识别精度较差；当激振频率很大时，即在D部分时，轴承主刚度识别误差最大，因此主刚度识别精度最差。

从图6中可以看出，当激振频率较小时，即在A和B部分，轴承主阻尼总体识别精度较好，但当试验台约束刚度很大时，主阻尼会产生较大的识别误差；当激振频率较大、约束刚度较小时，即在D部分，轴承主阻尼识别精度同样较好，但当试验台约束刚度较大时，即在E部分，轴承主阻尼识别误差产生增大趋势，主阻尼识别精度次之；在C部分，由于系统共振现象的存在，所以轴承主阻尼识别误差产生较大波动，主阻尼识别精度最差。

由于篇幅有限，文中针对试验台约束参数对轴承交叉刚度、交叉阻尼的影响不予详细分析。若将上述识别误差图的5个部分分为3个等级，识别精度“较好”部分表示为“++”，识别精度“次之”部分表示为“+”，精度“很差”部分表示为“-”，得到的试验台约束刚度对轴承动特性系数识别精度的影响规律如表2所示。

从表2可以看出，在A部分轴承动特性系数识别精度整体较高，因此，对于试验台结构设计而言，其约束刚度及激振频率选取在A部分比较合适，即试验台约束刚度的选取范围为2.42×102～2.541×105N/m，为试验轴承主刚度的0.000 3%～0.3%，且激振频率的选取范围为30～300 Hz。

3.3 约束阻尼的影响分析

当试验台约束阻尼为表1中初值的0.001～1 000倍时，在激振频率为0～1 000 Hz时试验台约束阻尼对轴承主刚度、主阻尼识别精度的影响规律分别如图7、图8所示。

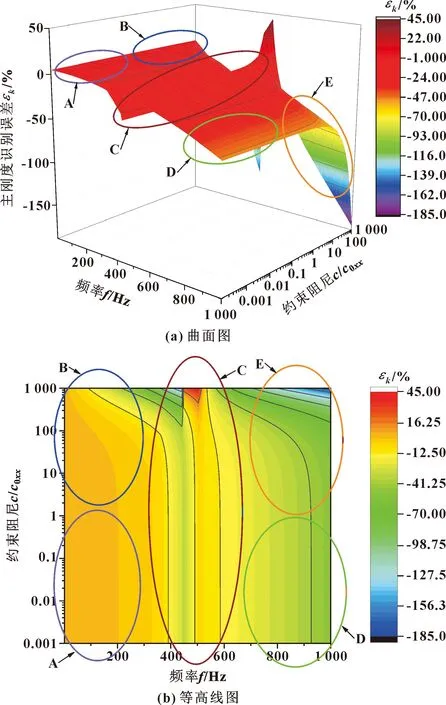
图7 不同约束阻尼时轴承主刚度的识别误差

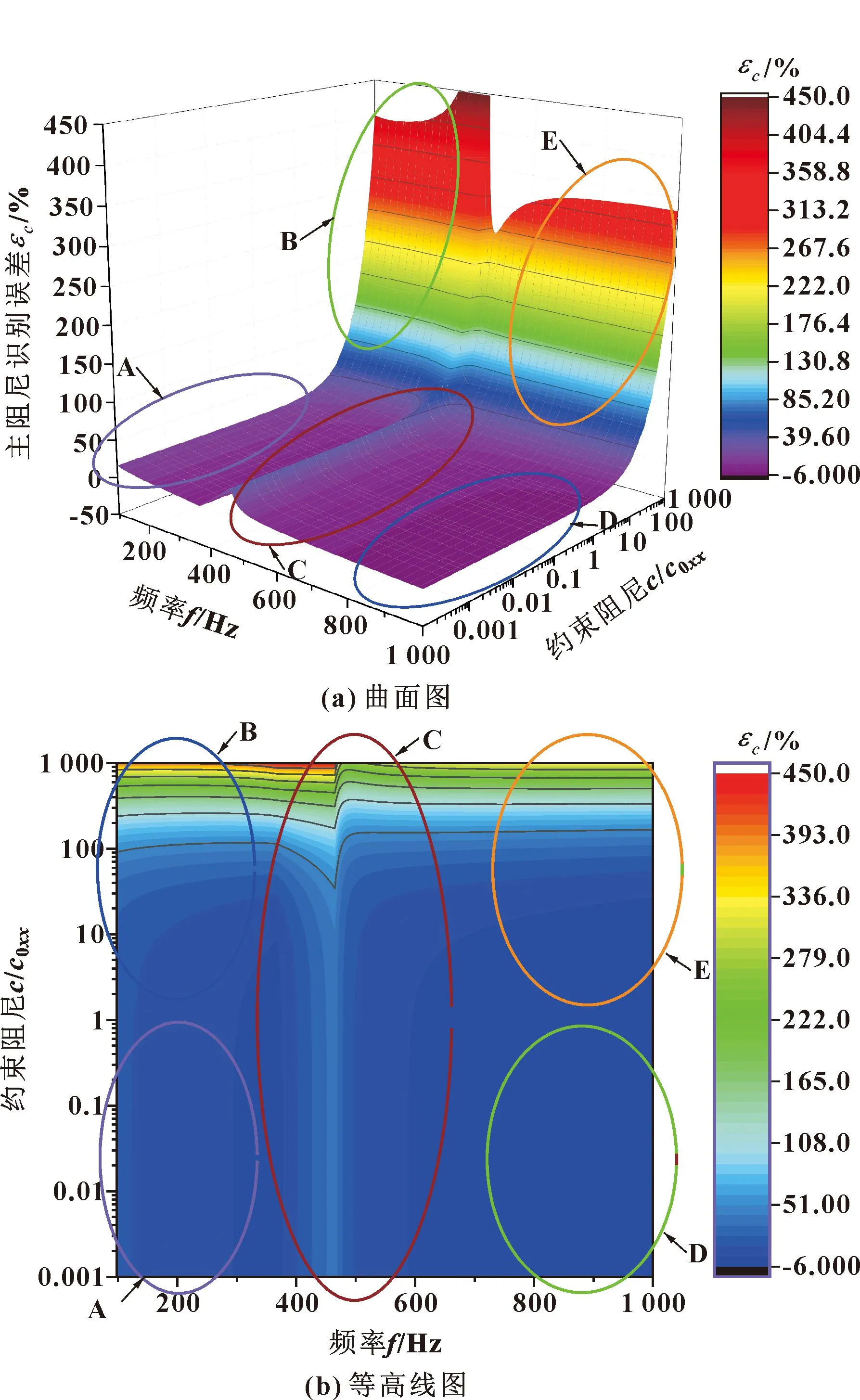
图8 不同约束阻尼时轴承主阻尼的识别误差

从图7中可以看出，当激振频率较小时，即在A部分时，轴承主刚度识别误差在0附近，主刚度识别精度较好；在D部分，轴承主刚度识别误差均有逐渐增大的趋势，主刚度识别精度次之；当试验台约束阻尼很大时，即在B和E部分，轴承主刚度识别误差较大；在C部分，由于激振频率与转子频率产生共振，所以存在较大波动，轴承主刚度识别误差最差，因此，主刚度识别精度同样最差。

从图8中可以看出，当试验台约束阻尼很小时，即在A和D部分，轴承主阻尼总体识别精度较好，但当试验台约束阻尼很大时，即在B和E部分，主阻尼会产生较大的识别误差；在C部分，由于系统共振现象的存在，所以轴承主阻尼识别误差产生较大波动，主阻尼识别精度最差。

同理，当试验台约束阻尼、激振频率发生变化时，将图7、图8按同样方式划分为5个部分，试验台约束阻尼对轴承动特性系数识别精度的影响规律如表3所示。