创设逐层递进的问题情境，发展学生的数学学科核心素养

黄雅倩

［摘  要］ 科学、合理的问题情境能有效激活学生的思维，引发学生思考与交流，发展学生的数学学科核心素养. 研究者以“弧度制”为例，从“情境创设，复习导入”“活动探究，形成概念”“揭露本质，建立联系”“应用新知，深化理解”“归纳总结，提炼升华”等方面展开教学，并从如下几点谈一些思考：注重渗透数学文化，激趣启思；关注知识内在联系，完善认知体系；加强提炼数学思想，发展素养.

［关键词］ 问题情境；核心素养；弧度制

科学、合理的问题情境往往能有效激活学生的思维，培养学生学习的内驱力，引发学生思考与交流. 基于学生的最近发展区设计逐层递进的问题情境，是践行新课标要求的基础，也是不断拔高学生思维、提升学生数学学科核心素养的保障. 为了验证这种说法，笔者对此进行了实践与研究，现以“弧度制”的教学为例，展开实践与思考.

教学分析

“弧度制”具有承上启下的作用，“上”为初中阶段所学的“度（角的度量单位）”，“下”为高中阶段推广的角的认识，学生在本节课前对“任意角”已有所了解. 本节课作为“三角函数”章节的第二课，教学初始目标在于引发学生认知矛盾，矛盾体现在“角度与三角函数值之间无法直接运算”方面，完成该目标，“弧度制”也应运而生. 关于“三角函数自变量与函数值的单位”问题的统一，可让角与实数之间形成对应的联系，这对后续研究任意角的三角函数以及函数相关运算等具有关键性的作用.

教学简录

1. 情境创设，复习导入

情境1 在正弦表的研究历程中，印度数学家阿耶波多意外发现在等式sin30°=0.5中，等号右侧的实数0.5与等号左侧的sin30°的单位制不同. 显然，这是一个矛盾. 在这种背景下，我们可否计算出sin30°+30°的具体值是多少？

设计意图 课堂起始阶段，将数学史料作为课堂导入的第一个情境，意在启发学生思考，让学生突破原本对问题封闭的认识，感知“角度”的正弦值实则为“实数”. sin30°+30°这个式子的提出，为学生思考指明了方向，即角度的正弦值与角度是否可以相加？sin30°为实数，而30°却是角的度数，因此两者并不具备相加的条件，由此成功引发了学生的认知冲突，为接下来的教学奠定了基础.

问题1 你们接触过哪些度量角的单位？

生1：初中阶段接触过度量角的单位有：度、分、秒.

师：这三个单位的进位制分别是什么？

生2：1度为60分，1分为60秒，因此为六十进制.

师：我们该如何定义1度的角呢？

生3：可将1度的角理解为周角的.

随着交流的深入，不仅勾起了学生对角度制的回忆，还促使学生自主抽象出什么是角度制，为接下来更加深入的探索做铺垫.

问题2 大家还记得之前的学习中，接触过哪些单位制可用来度量长度吗？它们各自的进位制是什么？

在这个问题的启发下，学生快速搜索知识结构，很快就总结出常见的度量长度的单位制有米、码、英尺等，而且这几种单位制均属于十進制.

师：既然度量长度的单位制有多种，那么度量角的单位制是否也存在多种呢？我们可否借助不同的单位制对角进行度量？能否应用十进制的实数来度量角的大小？

设计意图 旧知的复习意在让学生更清晰地理解度量角的单位制以及度量长度的单位制是什么，激发学生探索角度单位制的兴趣，为弧度制的引入做铺垫. 在类比思想的帮助下，学生初步感知知识间的联系，这对提升学生的数学抽象能力、类比推理能力等具有重要影响.

2. 活动探究，形成概念

探究内容 用十进制的实数来度量角的大小，需以“任意角”的定义作为出发点，探索与角度大小相关的量.

如图1所示，射线OA围绕端点O旋转至OB处形成角α. 在旋转过程中，射线OA上的一点P（非端点）形成的轨迹为一个圆弧，这个圆弧与圆心角α呈相对应的关系.

问题3 说说图1中射线OA在旋转时涉及哪些条件，所涉及的条件之间有没有什么关联点？

学生略作思考，很快就给出明确的结论：射线OA在旋转时涉及的条件有圆的半径、弧长与圆心角等，这些条件之间存在一定的关联性，如在半径不发生改变的背景下，圆心角的度数越大，则圆心角所对应的弧长也越长.

设计意图 调动学生已有的学习经验与认知基础，促使学生更好地建构与内化新知. 圆心角影响因素的研究顺利勾起了学生已有的认知经验，为抽象弧度制的概念奠定了基础.

3. 揭露本质，建立联系

师：正角、负角、零角受什么因素影响？

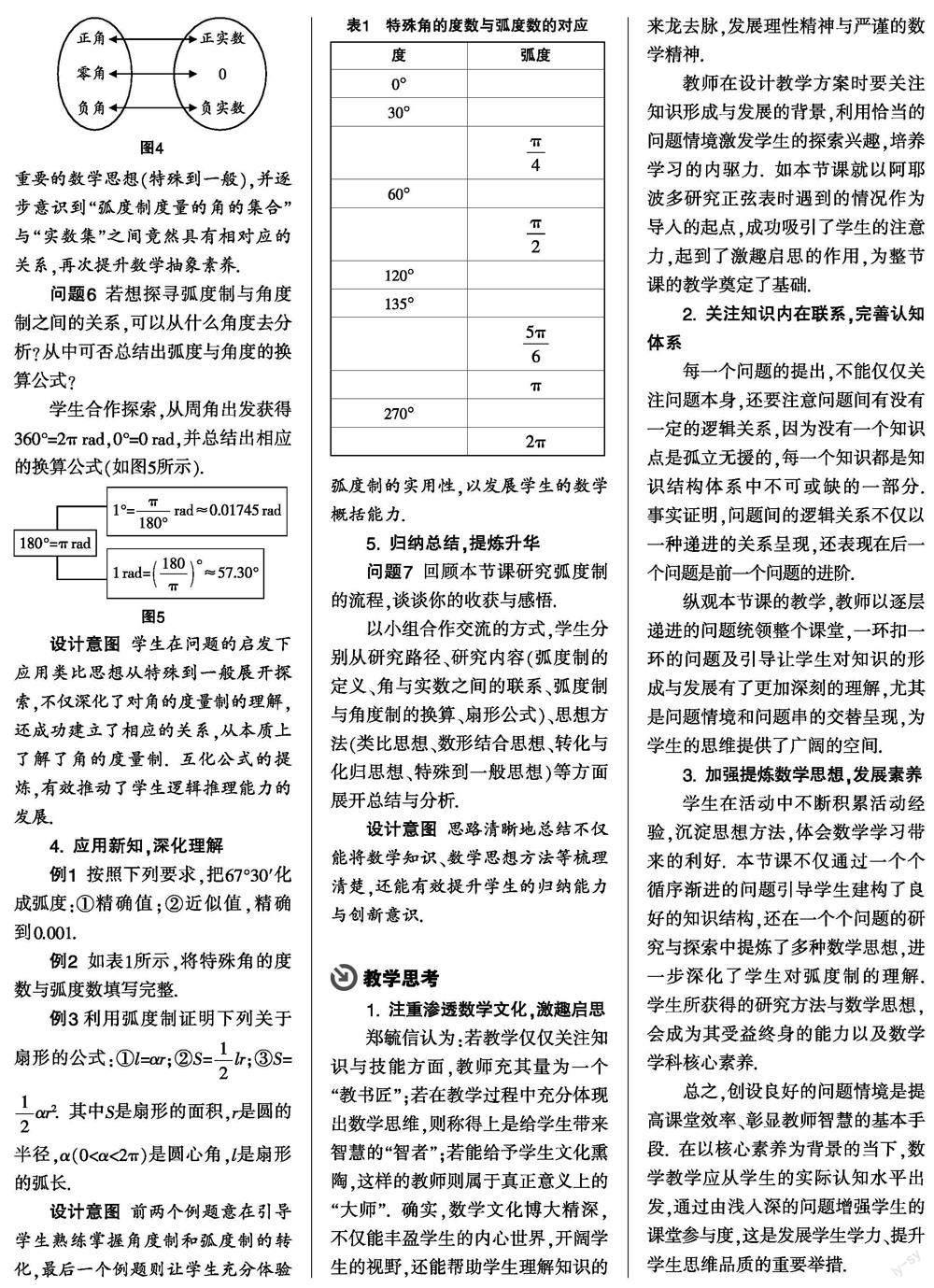
师：通过以上探索，大家觉得“弧度制度量的角的集合”与“实数集”之间有联系吗？

师生、生生积极互动，建立它们相对应的关系（如图4所示）.

设计意图 数学文化的渗透进一步激发学生对弧度制的研究兴趣，并深化学生对弧度制的认识. 学生在此环节感知到弧度制的本质，感悟到重要的数学思想（特殊到一般），并逐步意识到“弧度制度量的角的集合”与“实数集”之间竟然具有相对应的关系，再次提升数学抽象素养.

问题6 若想探寻弧度制与角度制之间的关系，可以从什么角度去分析？从中可否总结出弧度与角度的换算公式？

学生合作探索，从周角出发获得360°=2π rad，0°=0 rad，并总结出相应的换算公式（如图5所示）.

设计意图 学生在问题的启发下应用类比思想从特殊到一般展开探索，不仅深化了对角的度量制的理解，还成功建立了相应的关系，从本质上了解了角的度量制. 互化公式的提炼，有效推动了学生逻辑推理能力的发展.

4. 应用新知，深化理解

例1 按照下列要求，把67°30′化成弧度：①精确值；②近似值，精确到0.001.

例2 如表1所示，将特殊角的度数与弧度数填写完整.

设计意图 前两个例题意在引导学生熟练掌握角度制和弧度制的转化，最后一个例题则让学生充分体验弧度制的实用性，以发展学生的数学概括能力.

5. 归纳总结，提炼升华

问题7 回顾本节课研究弧度制的流程，谈谈你的收获与感悟.

以小组合作交流的方式，学生分别从研究路径、研究内容（弧度制的定义、角与实数之间的联系、弧度制与角度制的换算、扇形公式）、思想方法（类比思想、数形结合思想、转化与化归思想、特殊到一般思想）等方面展开总结与分析.

设计意图 思路清晰地总结不仅能将数学知识、数学思想方法等梳理清楚，还能有效提升学生的归纳能力与创新意识.

教学思考

1. 注重渗透数学文化，激趣启思

郑毓信认为：若教学仅仅关注知识与技能方面，教师充其量为一个“教书匠”；若在教学过程中充分体现出数学思维，则称得上是给学生带来智慧的“智者”；若能给予学生文化熏陶，这样的教师则属于真正意义上的“大师”. 确实，数学文化博大精深，不仅能丰盈学生的内心世界，开阔学生的视野，还能帮助学生理解知识的来龙去脉，发展理性精神与严谨的数学精神.

教师在设计教学方案时要关注知识形成与发展的背景，利用恰当的问题情境激发学生的探索兴趣，培养学习的内驱力. 如本节课就以阿耶波多研究正弦表时遇到的情况作为导入的起点，成功吸引了学生的注意力，起到了激趣啟思的作用，为整节课的教学奠定了基础.

2. 关注知识内在联系，完善认知体系

每一个问题的提出，不能仅仅关注问题本身，还要注意问题间有没有一定的逻辑关系，因为没有一个知识点是孤立无援的，每一个知识都是知识结构体系中不可或缺的一部分. 事实证明，问题间的逻辑关系不仅以一种递进的关系呈现，还表现在后一个问题是前一个问题的进阶.

纵观本节课的教学，教师以逐层递进的问题统领整个课堂，一环扣一环的问题及引导让学生对知识的形成与发展有了更加深刻的理解，尤其是问题情境和问题串的交替呈现，为学生的思维提供了广阔的空间.

3. 加强提炼数学思想，发展素养

学生在活动中不断积累活动经验，沉淀思想方法，体会数学学习带来的利好. 本节课不仅通过一个个循序渐进的问题引导学生建构了良好的知识结构，还在一个个问题的研究与探索中提炼了多种数学思想，进一步深化了学生对弧度制的理解. 学生所获得的研究方法与数学思想，会成为其受益终身的能力以及数学学科核心素养.

总之，创设良好的问题情境是提高课堂效率、彰显教师智慧的基本手段. 在以核心素养为背景的当下，数学教学应从学生的实际认知水平出发，通过由浅入深的问题增强学生的课堂参与度，这是发展学生学力、提升学生思维品质的重要举措.