基于三维空间的激光驾束炮射导弹设计及外弹道仿真

李冬青，朱 胤，朱元武，王 倩，黄海英

（北方自动控制技术研究所，太原 030006）

0 引言

激光驾束炮射导弹由于具有作战灵活，打击精度高，成本低，可靠性高等众多优势［1］，在近年来的一些局部战争都发挥着独特的作用，各个国家都在不断对其进行改进研制。炮射导弹是陆域战争典型的武器装备，但是其数据都为各国的机密，为了提高局部陆域战争打赢实力，改进性能和评估制导精准度及毁伤效果，促进导弹设计国家所需人才培养建设，需要对激光驾束炮射进行整体外形设计并且导弹进行外弹道仿真，炮射导弹三点法导引具有简单容易实现的特点，但先前的研究者基本没有研究在三维空间地状态下对炮射导弹的弹道进行模拟［2-3］，只是在简单的在二维平面对目标运动进行理想化假设，这严重不符合实战中目标具有不可控制、运动随机的特点。本文创新性地建立炮射导弹三维空间运动学方程，并运用三点法对具有随机运动特性的目标进行弹道仿真，可以减少实弹打击所带来的不确定性和成本偏高等问题，因此，具有实际作战意义；本文还创新性地对导弹总体进行完整便捷的设计，并对导弹气动特性运用便捷精准的方法进行获取，对初学者进行导弹设计仿真具有很好的指导作用。此外，激光驾束炮射导弹外弹道仿真还能对导弹总体设计提供相关的性能参数，对炮射导弹的不断研发和改进具有借鉴参考的意义。装备模拟器是面向战争实景的新型战术仿真系统的重要构成之一，随着仿真技术在军事方面的快速发展，通过装备模拟器构建三维场景来检验武器装备作战性能，炮射导弹弹道仿真在装备模拟器中的应用，将会促进人机实时交互军事训练模拟系统的不断发展和完善。

1 炮射导弹外弹道数学模型的建立

1.1 坐标系的建立及转换

本文研究的是激光驾束炮射导弹，其原理为炮射导弹打击目标时，射手用瞄准制导仪瞄准、跟踪目标，炮弹发射后制导系统会发射一道激光束，并按期望沿着激光束中心飞行，直到击中目标。

虽然炮射导弹的运动规律不会因为坐标系的选取而发生改变，但是在计算时会因为坐标系的选取而导致运动方程的复杂程度不同，导弹的姿态、受力的大小和方向，以及速度的大小和方向都受到坐标系的选取不同而形式不同，为了便于对导弹运动方程分析，建立不同的坐标系很有必要，下面将介绍本文所用的导弹坐标系及其转换。

1.1.1 基准坐标系Oxyz

基准坐标系Oxyz 与导弹固连，是一个动坐标系，其原点O 为导弹的瞬时质心，为了便于分析，不考虑瞬时质心位置的变化。Ox 轴为水平基准方向，沿目标方向为正，Oz 垂直于Oxy 平面，方向按右手准则确定。

1.1.2 弹道坐标系Ox2y2z2

弹道坐标系的Ox2y2z2与导弹的速度矢量固连，是一个动坐标系。弹道坐标系的原点O 也在导弹的瞬时质心上，Ox2轴沿着导弹的速度矢量方向，沿速度矢量方向为正；Oy2轴在包含Ox2的铅垂平面上，方向以向上为正；Oz2轴与Ox2y2平面垂直，右手准则确定Oz2的方向。弹道坐标系通常用来确定导弹的偏转以及导弹质心运动的动力学方程。

1.1.3 基准坐标系与弹道坐标系的转换

弹道坐标系可视作由基准坐标系以旋转φv→θ为次序，经过两次旋转而来。因此，可以直接得到弹道坐标系与基准坐标系之间的转换公式，如式（1）所示，其中，φv为弹道偏角，θ 为弹道倾角。

1.2 炮射导弹运动方程组的建立

导弹在飞行时，发动机作为推进剂会消耗燃料，导弹质量受推进剂消耗燃料质量影响，消耗燃料产生的发动机推力P 如式（2）所示［4］。

式中，mc为燃料消耗量的变化率，ue为喷管燃气排放速度，Se为喷管横截面积，Pe为喷管燃气压强，PH为导弹所在位置的大气压强。推力大小具体数值可以在试验台上测得，本文查阅相关资料，为了便于分析炮射导弹的外弹道轨迹，将导弹的推力大小及质量变化率较为理想地按式（3）计算：

由于攻角较小，可以忽略偏转给导弹带来的影响，因此，炮射导弹质心运动方程可以简化为式（4）［5］：

1.3 炮射导弹导引模型的建立

三点法属于遥控制导的一种导引方法，因其原理简单，容易实现，成为导弹制导的常用导引方法。三点法是指导弹在追寻目标的飞行过程中，从制导站看去，移动制导站时，制导站、导弹和目标始终在一条直线上。本文选取三点法作为炮射导弹的导引规律，并从三维空间出发，建立导引方程［6］，其原理图如图2 所示。

图中，R、Rm分别为制导站到导弹和目标的距离，ε、η 分别为导弹的高低角和偏航角，εm、ηm分别为目标的高低角和偏航角。

由上图可以得知三点法导引的关系方程为：

根据制导站与导弹之间、制导站与目标之间的相对运动关系，由运动学规律可得到制导站与导弹、制导站与目标的运动学方程组，如式（6）所示：

式中，vm为运动目标的速度，θm为目标的弹道倾角，φvm为目标的弹道偏角。

2 炮射导弹结构设计及参数分析

炮射导弹整体结构的设计对气动特性分析和导弹外弹道轨迹变化有着重要的影响［7］，因此，对炮射导弹的整体结构参数的设计有着十分的必要性，本文为了保证炮射导弹整体结构参数的合理性，参考了俄罗斯的“芦笛”号炮射导弹［8］，查阅相关资料可得到“芦笛”炮射导弹的主要战术技术性能指标，其具体参数如表1 所示。

表1 “芦笛”炮射导弹主要战术性能指标Table 1 Main tactical performance indexes of“Ludi”gun-launched missile

2.1 炮射导弹气动外形设计

炮射导弹气动外形设计对导弹是否具有良好的气动性能以及是否满足对机动性、稳定性和操纵性的要求十分重要。气动外形设计主要包括气动布局的选择和各部件外形几何参数的确定。

2.1.1 气动布局的选择

导弹气动布局的选择需要对弹翼、舵面和发动机等各部件之间的相互位置进行合理的确定安排，在对质心定位的计算中给出了对各部位的位置安排。研究导弹的气动布局可以聚焦到以下两个问题：

1）翼面（包括弹翼、舵面等）数目及其在弹身周侧的布置方案；

2）翼面之间（如弹翼与舵面之间）沿弹身纵向的方案布置。

本文参考“芦笛”炮射导弹，结合考虑轴对称具有简便计算，每个方向上产生升力都会使导弹舵机系统能够得到快速的响应，最终确定轴对称布置方案，尾翼选取×字形弹翼。

2.1.2 各部件几何参数的确定

各部件几何参数的选择和几何尺寸的确定，对炮射导弹的气动特性分析都有着重要的影响，因此，需要对弹翼的展弦比λ、根梢比η、前缘后掠角χ这3 个参数分别进行分析。以上3 个参数的具体影响不再详细展开，具体参数如表2 所示。

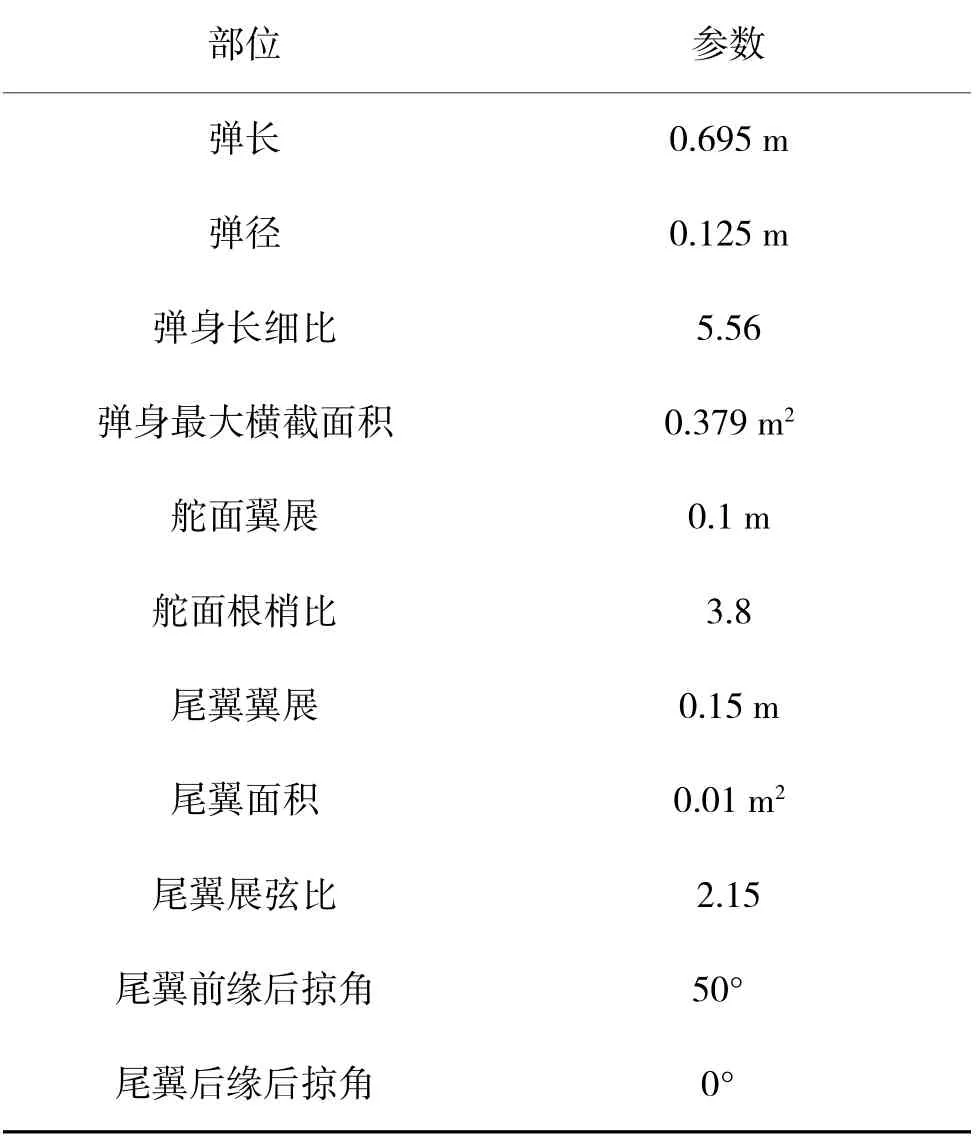
表2 炮射导弹各部位几何参数Table 2 Geometric parameters of various parts of gun-launched missile

对弹翼的展弦比λ、根梢比η、前缘后掠角χ 这3 个参数分析完后，还需要对弹翼的翼型进行选择，超声速导弹的常见翼型如图3 所示，考虑到飞行速度大小和工艺性结构，本文选取的翼型剖面是六边形。

对于弹身外形的形状及参数大小，对导弹的气动特性影响也不可忽略。导弹弹身分为头部、中段和尾部。有翼导弹的头部外形通常有锥形、抛物线形、尖拱形和半球形，综合考虑导弹气动力及制导要求，本文选取尖拱形作为炮射导弹的头部外形。导弹的中段外形通常选取圆柱形，能够在提高空间的同时减小空气阻力。导弹的尾部一般有平直圆柱形、锥台型和抛物线形3 种，考虑到空气阻力较小，加工较简单，一般导弹都选取锥台型作为导弹的尾部形状。

2.2 炮射导弹总体部位安排

2.2.1 炮射导弹总体部位

为了保证炮射导弹能够从炮射口到精准击中目标这一过程中，导弹能够具有良好的稳定性和操纵性，往往需要对炮射导弹进行总体部位安排［9］。

导弹的稳定性是整体设计的重要指标之一，衡量导弹稳定性通常需要考虑静稳定性指标和动稳定性指标。考虑到导弹静稳定一定动稳定，但动稳定不一定静稳定。因此，在本文的研究设计中，保证了导弹具有一定的静稳定度。

2018年10月11日，雅马哈株式会社社长中田卓也、全球营业本部本部长山口静一等一行亲临展会现场，在雅马哈（中国）公司总经理鹤见照彦、钢琴营业部部长刘朋、客户服务部部长新美哲嗣等的陪同下视察了雅马哈钢琴展区。

为了确定导弹的压心和质心确定位置，需要考虑试验与计算误差的约束边界

综合以上因素可得到

式中，LB为导弹长度。

通过后文的质心定位，可以得到导弹的质心位置为0.362 9 m，压心位置为0.421 6 m，经过仿真计算论证分析，该导弹的质心位置和压心位置完全满足导弹飞行过程中对稳定性和操纵性的要求。

2.2.2 炮射导弹各部位质心定位

本次炮射导弹的质心定位设计是参考俄罗斯的“芦笛”炮射导弹，各个质量参数也是在多次论证可行后加以确认的，为了确保导弹在飞行过程中满足导弹对静稳定度的要求，本文在设计时需要反复调整各个部件的位置，确定各个部件的质心位置，结合相关参考资料，最终设计的炮射导弹各部位质心及相关参数表3 所示。

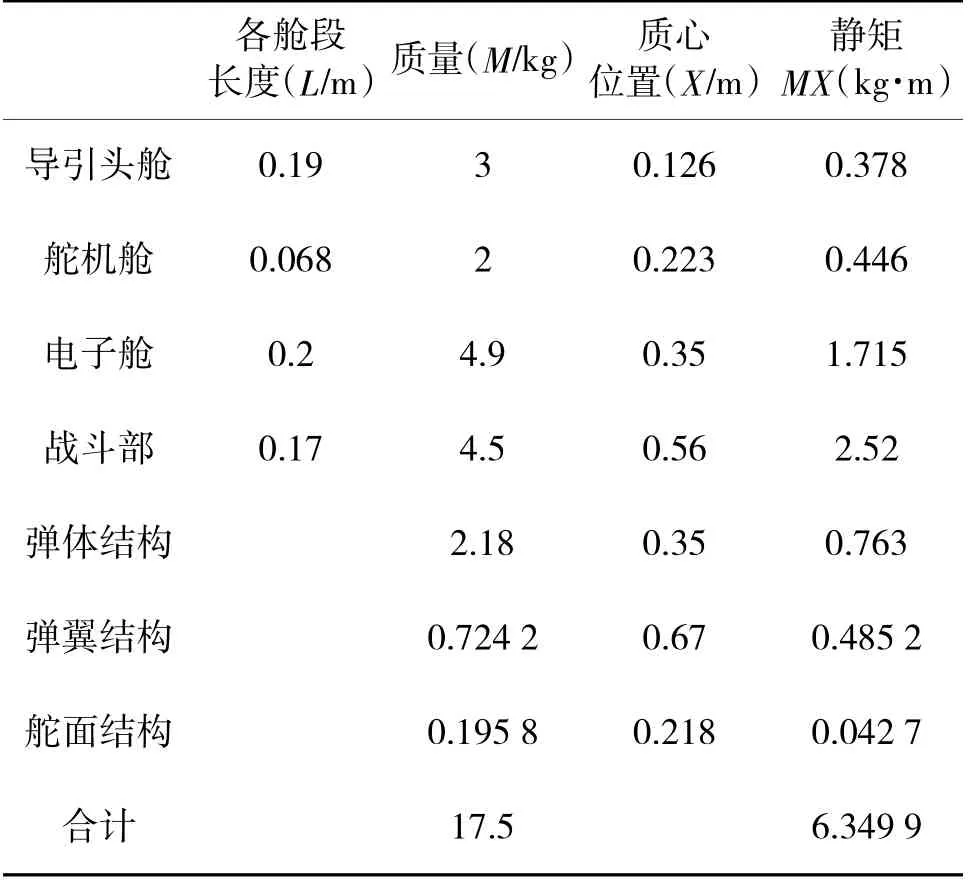
表3 炮射导弹各部位质心位置及相关参数Table 3 Centroid position and related parameters of each part of gun-launched missile

由理论力学中的力矩平衡原理可知，导弹的质心位置计算公式为：

通过质心计算公式可求出炮射导弹的质心位置：

Tecplot 是一款功能强大的数据分析和可视化处理软件。它提供了丰富的绘图格式，包括x-y 曲线图，多种格式的的2-D 和3-D 面绘图。为了便于直观分析，利用Tecplot 软件建立起导弹的三维模型，如图4 所示。

3 基于Missile Datcom 的炮射导弹气动特性分析

3.1 炮射导弹气动特性方法的选取

为了求出气动力和气动力距，一般有数值计算法、风洞实验法和工程计算法［10］，但是数值计算法不仅计算量大，还对电脑CPU 等硬件的性能设置了门槛，耗用时间过长，不适合在导弹的初步设计过程中使用，而通过风洞试验法来准确模拟导弹在飞行过程中受到的环境状况及获取导弹的气动力系数比较困难。本文主要选取工程计算法，选取的软件是Missile Datcom［11-13］。Missile Datcom 是由美国空军飞行力学实验室开发的一款气动力工程计算软件，采用了部件组合法、数据模块化和方法模块化等方法。由于其充分利用了美国空军几十年来的风洞试验数据，因此，它对于一般传统外形设计的导弹具有较强的适应性和较高精度。随着技术的发展和试验数据的积累，该软件的功能和试验数据不断完善，计算结果的精确度也不断提高，成为美国飞行器总体设计部门必备的程序。

3.2 Missile Datcom 使用流程及结果

Missile Datcom 软件一般分为无界面版，有界面版1 号和有界面版2 号3 种，本文选取的是2011版的有界面版2 号，具体见图5，将第3 章中设计的导弹参数依次利用Missile Datcom 软件进行编辑。

限于文章篇幅，下面直接给出Missile Datcom 软件部分计算结果，以下各图均是在马赫数为1.2 时，各气动力系数和气动力矩系数随攻角变化的情况。

4 炮射导弹外弹道仿真及结果分析

4.1 仿真方法的选择

MATLAB 软件具有简单易行，可视化操作强等众多优点，因此，本文选取MATLAB 软件作为仿真软件。对炮射导弹气动特性的分析可知，升力系数、阻力系数、偏航力矩系数主要受速度和攻角影响，侧向力系数、偏航力矩系数和滚转力矩系数主要受速度和侧滑角影响，因此，可以将Missile Datcom 得到的表格中的数据提取并导入到MATLAB 进行二维差值，从而可以得到其变化规律。对于炮射导弹动力学和三点法构成的微分方程组，由于弹道是连续的，并且弹道解算要求精度高，因此，可采用变步长的四阶龙格库塔法［14］进行求解运算。

4.2 仿真结果及分析

4.2.1 气动特性的仿真结果及验证

气动特性参数通过Missile Datcom 软件获取，将获取的数据制成Excel 表格，使用MATLAB 软件进行数据的读取，并通过二维插值仿真得到以下仿真结果。

在本文给定的气动布局和结构外形设计下，由图14～图16 分别可以看出，阻力系数随着马赫数的增加先增大后减小，在马赫数接近于1 时，导弹的局部和头部形成激波导致阻力系数急剧增大，在攻角比较小时，随着攻角的增大，阻力系数明显地也随着增大；在小攻角情形下，升力系数随马赫数的增加先增大后减小，可以看出在马赫数为1 左右时，升力系数会出现猛跌现象，对于攻角，随着攻角的增大，升力系数明显的也随着增大；小攻角情形下，侧向力系数随着马赫数的变化不是很明显，随着侧滑角的增大，侧向力系数不断减小。本文得到的结论与参考的一些文献资料中的结论一致，说明本文的导弹气动外形设计合理，通过Missile Datcom得到的气动数据较为准确，为炮射导弹的导弹仿真确定了准确的仿真数据。

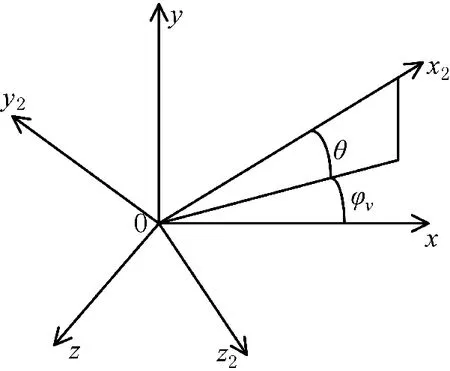
图1 弹道坐标系与基准坐标系的关系Fig.1 The relationship between ballistic coordinate system and reference coordinate system

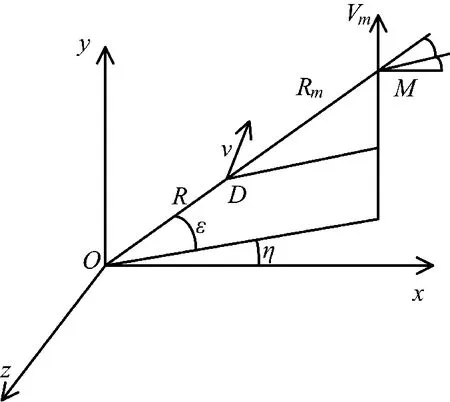
图2 三点法原理图Fig.2 Schematic diagram of three-point method

图3 超声速导弹常见翼型Fig.3 Common airfoils for supersonic missiles

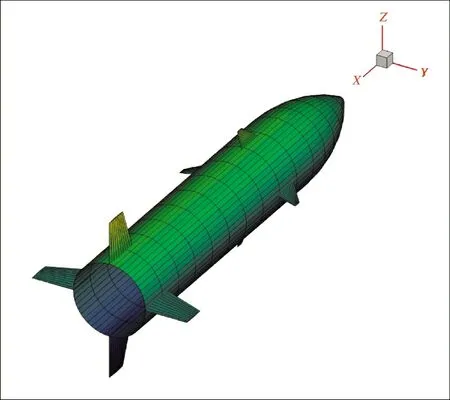
图4 炮射导弹三维模型Fig.4 Three-dimensional model of gun-launched missile

图5 Missile Datcom 软件操作界面Fig.5 Operation interface of Missile Datcom software

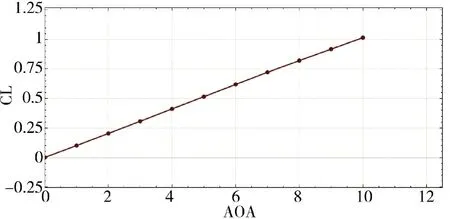
图6 升力系数随攻角变化Fig.6 The lift coefficient varies with angle of attack

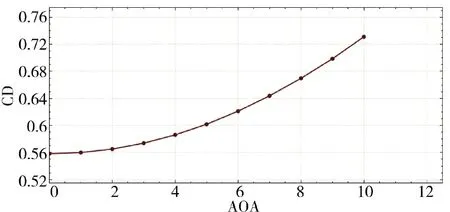
图7 阻力系数随攻角变化Fig.7 The drag coefficient varies with angle of attack

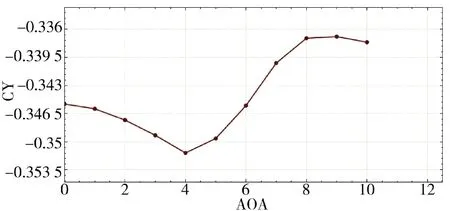
图8 侧向力系数随攻角变化Fig.8 The lateral force coefficient varies with the angle of attack

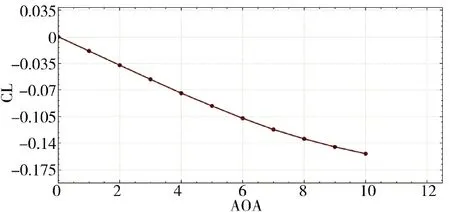
图9 俯仰力矩系数随攻角变化Fig.9 The pitching torque coefficient varies with the angle of attack

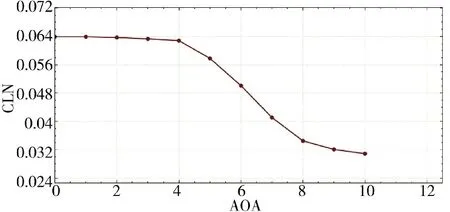
图10 偏航力矩系数随攻角变化Fig.10 The yaw torque coefficient varies with the angle of attack

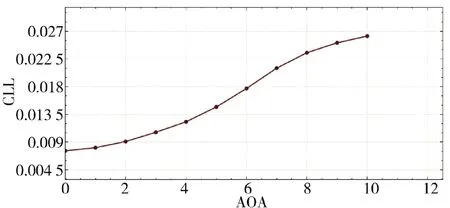
图11 滚转力矩系数随攻角变化Fig.11 The rolling torque coefficient varies with the angle of attack

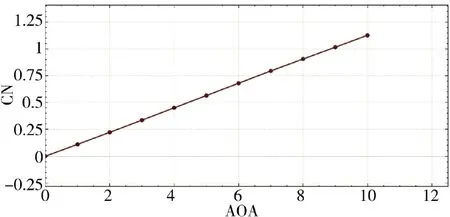
图12 法向力系数随攻角变化Fig.12 The normal force coefficient varies with the angle of attack

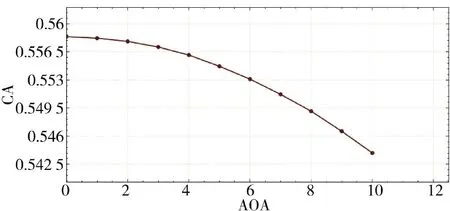
图13 轴向力系数随攻角变化Fig.13 The axial force coefficient varies with the angle of attack

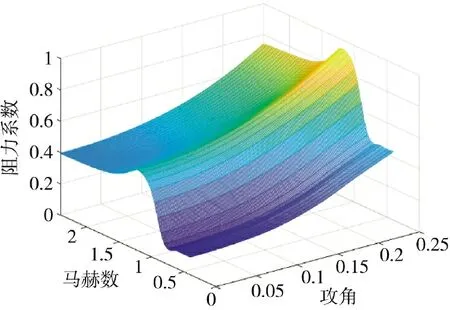
图14 阻力系数随攻角及马赫数变化Fig.14 The drag coefficient varies with angle of attack and Mach number

图15 升力系数随攻角及马赫数变化Fig.15 The lift coefficient varies with angle of attack and Mach number

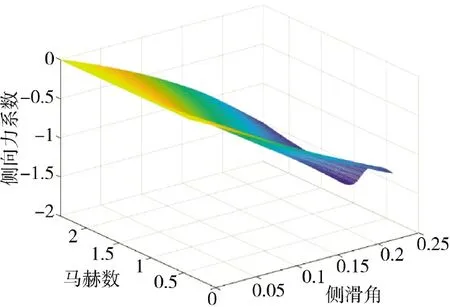
图16 侧向力系数随侧滑角及马赫数变化Fig.16 The lateral force coefficient varies with the slip angle and Mach number

4.2.2 炮射导弹弹道的仿真结果及验证

本文可以实现在较低成本下实时获取目标的动态三维飞行数据，坦克可以安装陀螺仪测高低角和方位角的角速度（通过转动激光制导器获取），激光测距仪来解算目标实时速度，通过上文建立的炮射导弹运动方程组与导引模型的结合，从而可以达到在三维空间目标任意飞行状态下依旧可以达到精确制导的效果。

为了便于分析，本文设定的初速度v=400 m/s，为了保证炮射导弹在炮口发射时能准确处于激光束中心附近，在反复实验仿真下，确定了初始弹道倾角为θ=20π/180［15］，弹道偏角为ψv=0，取坐标初始值x=y=z=0，初始高低角ε=20π/180，初始偏航角η=0，R=0，Rm=7 000，m=17.5，为了方便分析，在三维空间下简化目标的运动状态，由上文获取的目标动态三维飞行数据，其相对制导站的运动方程组为：

结合式（12），通过MATLAB 软件采用变步长的四阶龙格库塔法进行仿真计算，当R＞Rm时，仿真结束，得到的仿真结果如图17～图20 所示。

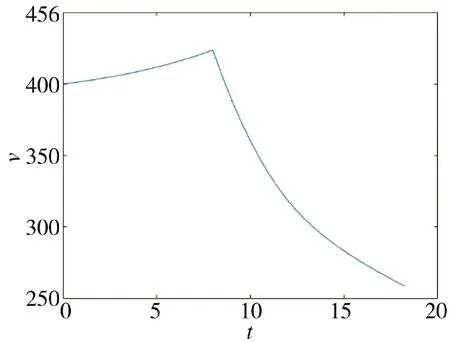
图17 速度随时间变化图Fig.17 Variation of speed with time

由图17 可以看出速度在8 s 时达到最大值，同时弹道倾角、攻角、侧滑角也在8 s 时发生明显变化，这是由于推进剂结束，炮射导弹受到的空气动力发生改变；图18 表明弹道倾角在速度降低后变化明显放缓，更为平稳，具有较好的跟随性；从图19可以看出攻角和侧滑角变化角度幅度变化较小，因此，整个炮射导弹的飞行过程较为稳定；图20描述的是炮射导弹和目标的运动轨迹图，两条轨迹相交于一点，表明炮射导弹精准击中目标，达到预期效果。

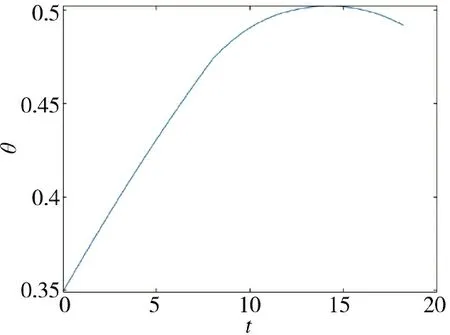
图18 弹道倾角随时间变化图Fig.18 Variation of trajectory inclination with time

图19 攻角、侧滑角随时间变化图Fig.19 Variation of attack angle and sideslip angle with time

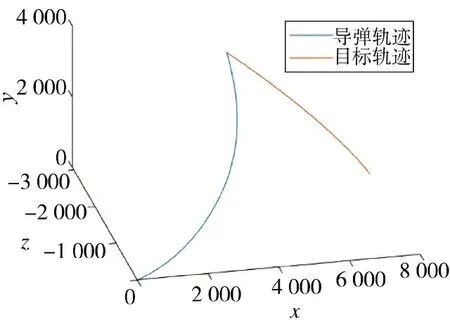
图20 炮射导弹和目标运动轨迹图Fig.20 Trajectory diagram of gun-launched missiles and targets

5 结论

本文完成了炮射导弹的总体设计，并获取了导弹的气动特性，在三维空间下建立三点法导引模型，对任意运动目标进行打击弹道仿真，最终在模拟中实现对目标的精准打击。仿真的最终目的在于应用，激光驾束炮射导弹外弹道仿真的原理及平台的搭建，对于其他导弹及相关武器具有通用性，对建立具有人机实时交互军事训练模拟系统也有着很重要的意义。未来将建立炮射导弹的动态数据库，使炮射导弹弹道仿真与装备模拟器结合，做到虚实相衬、算法调优、效能评估，通过修改炮射导弹的参数，便能实现对各种炮射导弹的半实物仿真。