500kg激光制导炸弹效能指标量化方法在评估中的应用*
2024-04-16唐璐琪郭亮亮
杨 平,肖 兵,陈 新,唐璐琪,郭亮亮
(1.空军预警学院,武汉 430000;2.解放军93052 部队,长春 130021)
0 引言
武器系统的效能评估,是指在特定的使用环境(作战环境、作战任务、气候环境、作战流程以及武器装备自身性能等)和条件下武器系统完成给定作战任务的能力。比较有代表性的评估方法有ADC法、量化标尺法、层次分析法等解析法,还有模糊综合评判与灰色理论综合集成法、云模型等综合技术与方法[1-6]。武器装备的效能评估涉及衡量指标、权重和聚合方法等一系列要素的确定,其中,评估指标值量化更是评估工作中最为重要的。
为提高评估结果的准确性与可信度,王睿等提出一种基于专家可信度与区间值集结的定性指标量化方法[7];王亚鹏等提出“装备体系和谐”的概念内涵,以协调、增效和发展三大量化准则为框架,装备体系和谐评估指标与量化方法具有一定的科学性、合理性与操作性[8];文章结合灰色理论提出了一种基于灰色AHP 的性评估指标量化方法[9];吴志飞等提出了一种对指标进行去模糊化处理,再次利用遗传算法对去模糊处理过程中的偏置量进行计算的指标量化方法[10]。上述几种处理方法仍旧是在不同层面上引入了主观不确定因素,以及在准则与尺度的设立上没有一个明确的界限。
针对评估指标在量化中出现的问题,以500 kg激光制导炸弹的效能评估为例,重点对能力向量进行拓展,分析关键评估指标。对量纲类指标提出了基于相关性隶属度函数的指标量化方法,观测数据的输入到量化指标的输出,过程清晰合理;对于概率类指标,按定量和定性分成两类,对定量类指标采用代定函数法,输入相应参数得到效能值;对于定性类指标当中的部分指标,本文重新定义了粒子群优算法的适应度函数,利用样本的航迹适应度值与适应度优化区间的比值归一化后作为效能指标。将所有指标进行无量纲化处理后进行求和聚合得到综合参数,代入评估模型得到最终评估结果。
1 系统效能建模步骤
本文主要是针对激光制导炸弹武器系统效能的评估,模型整体架构上采用的是ADC 法。系统效能E 可以表示为:
式中,A 为系统可用性向量;ai为系统初始时i 状态的概率;n 为武器系统可能的状态数;D 为系统的可信度矩阵;dij为系统在工作过程中状态由i 转入j的概率;C 为系统的能力向量;cj为系统在状态j 中完成任务的能力。
本文对指标的处理整体上进行分层和分类,对每类每层采用不同的方法,考虑载机生存能力、突防能力、目标探测能力等综合性指标,使系统综合效能的评估更趋完善,重点对能力向量进行拓展,对于分离出的可靠性指标,采用比例计算法来得到可用性,采用指数计算法来得到可信度;在指标权重的确定上除应用传统作战模拟法、专家评定法、层次分析法等方法之外,还应用了机器学习算法的分类模型,基于信息熵理论,确定了指标权重。参照评估指标体系建立的5 个原则[11],结合作战流程与原始数据建立效能评估指标体系,如图1 所示。
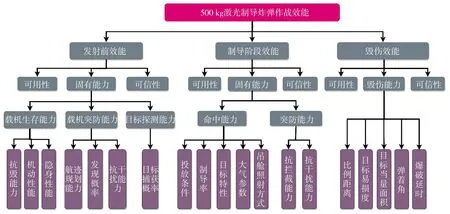
图1 激光制导炸弹效能评估指标体系Fig.1 Laser-guided bomb effectiveness evaluation index system
由于受到敌方防区范围、载机性能、目标属性、武器的性能参数等因素的影响,本文将效能评估分为3 个阶段,分别是武器发射前的效能、武器飞行制导阶段的效能以及命中毁伤效能,采用加权求和策略得到总体任务效能。因此,式(1)可以改写为:
其中,EG为总体任务效能;εi为第i 阶段效能的权重;AiDiCi为第i 阶段的效能值。
2 系统可用性模型建立
可用性向量A 表示系统在开始任务执行时可能处于的状态,对于武器系统通常指处于良好或故障状态。如果有n 种可能的状态,则为一个n 维向量,即
式中,ai为武器系统任务初始时状态i 的概率;n 为武器系统可能的状态数。
激光制导武器系统是由多个子系统组成,包括瞄准/制导系统、发射系统、飞行控制系统与引战系统。按照激光制导炸弹的作战流程,载机火控系统捕获目标,激光吊舱对目标进行连续照射,发射指令发出后发射系统动作,武器离开载机后制导系统、武器飞行控制系统、引战系统为并行工作状态。简化之后武器各子系统的串、并联结构如图2所示。

图2 激光制导炸弹武器系统串、并联关系图Fig.2 Laser-guided bomb weapon system series and parallel relationship diagram
为便于研究,假定载机携带单枚激光制导炸弹,并且各系统的初始状态一旦确定,故障状态的系统在执行任务阶段是无法自动修复的。系统的合并处理是必要的,将串联结构合并成一个单元,载机的火控系统与发射系统合并(称C 系统);制导与飞行控制系统(称G 系统),包括激光指示吊舱、导引头、中控机以及飞行控制组件;引战系统(简称为F 系统),G 与F 为并联结构。其中串联系统的可用度为发射前效能的可用度,制导与飞行控制系统的可用度为制导阶段效能可用度,引战系统的可用度属于毁伤效能阶段可用度。
激光制导炸弹武器系统由多个功能组件组合而成,可能处于多种工作状态,若考虑武器系统所有状态数,即使是合并后,可用性向量A 的维数仍非常大。另一方面,状态数过大还将导致可信度矩阵D 无法计算。因此,通常只考虑两个典型状态,即可用状态与故障状态。不同的系统状态对应效能评估的3 个阶段,可能存在的状态数为6 种:S1:C 正常,串联系统可用;S2:C 故障、串联系统故障;S3:C正常、G 正常,系统可用;S4:C 与G 至少一个故障,系统故障;S5:C 正常、G 正常、F 正常,系统可用;S6:C 正常、G、F 至少一个故障,系统故障。
S1、S2 为第1 阶段两种状态,S3、S4 为第2 阶段两种状态,S5、S6 为第3 阶段两种状态。由此,第1 阶段的效能只与C 系统有关,与G、F 系统状态无关。G 系统与F 系统属于并联关系,由于C 系统的正常工作是G、F 系统正常工作的初始条件,因此,第2 阶段只考虑制导与飞行控制系统的可用性即可。G 系统的工作状态不影响F,制导系统的正常工作可以确保命中目标,而命中是评估毁伤效能的前提,虽然G 系统与F 系统结构上是并联关系,但逻辑关系是串联关系。因此,第3 阶段的可用性可按串联系统计算。系统的可用性取决于平均故障间隔(MTBF)和平均修复时间(MTTR),则可用性向量A可以表示为[12]:
其中,MTBFi为第i 个子系统的MTBF;MTTRi为第i个子系统的MTTR。
3 系统可信度模型建立
可信性是效能模型中的另一个重要因素,它是系统效能的重要属性,它跟可用性的不同之处在于:系统的可用性是一个静态的物理量,是对武器系统在执行任务前装备系统可靠性的描述,而可信性是一个动态过程,描述武器系统在执行任务过程中是否具有稳定性和持续作战能力。由上文的假设条件,则不可修复的制导炸弹武器系统可信性矩阵可表示为[12]:
式中,dij表示武器系统在开始执行任务时,状态di向该武器系统执行任务t 时刻dj状态转移的概率。矩阵中各元素满足
3 个效能评估阶段,系统故障不可进行自我修复。每个阶段分别由两种状态,共6 种状态,状态转移关系如图3 所示。

图3 激光制导炸弹状态转移图Fig.3 State transfer diagram of laser-guided bomb
第2 阶段的效能评估是基于第1 阶段串联系统正常的基础上,如果不能正常发射,武器飞行控制系统自然无法启动,同理,如果武器的制导与飞行控制系统故障导致无法命中,单纯讨论毁伤效能是没有意义的。即前一个阶段系统的正常是下一个阶段的初始条件。则3 个阶段的可信性矩阵为:
其中,RC、RG、RF为系统的可靠性,这类系统的可用性通常成指数分布,通过任务时间可求得。
4 系统能力模型建立
由于制导炸弹武器系统任务目标的收敛性,若马尔科夫假设成立,则
式中,cj的含义是制导炸弹武器系统在状态j 中完成任务的概率。为准确获得系统能力参数cj,性能指标的选取和处理问题是关键,其量化表征是其下层指标的几种体现,反映出武器的基本性能、战场环境、适用范围等。
4.1 效能指标的分类
本文选用的激光制导炸弹武器系统效能指标有3 类。
1)量纲类指标:比例距离、平均毁伤面积、弹着角以及影响命中能力的若干指标;
2)定量概率类指标:载机被发现概率、目标捕获概率;
3)定性概率类指标:载机抗毁能力、载机机动性能、载机隐身性能、航迹规划质量、载机抗干扰能力、武器的抗拦截能力与抗干扰能力等。
4.2 效能指标的量化
在指标分类的基础上,应采取不同策略对不同的指标进行量化,使量化后的指标更能准确反映出武器在复杂环境中的真实表现。
4.2.1 量纲类指标量化
不同的量纲类指标是由不同区间的数值组成,某一指标的数值所代表的是武器在该方面的能力,而这些数值是无法直接表示其能力的,因此,需要有效的方法将数值转化为能力值。为此,本文对于量纲类指标量化的基本思路是:1)判断子类指标与父类指标的相关性,将无关指标去除;2)分析数据分布状态,应用曲线拟合的方法,得到指标数据的概率分布函数;3)根据文献[14]所提出的区间分位数最大相关性准则,即子类指标的最大相关系数所在区间,与源数据所在区间进行比较,确定指标边界值;4)结合指标边界值将指标概率分布函数更新为隶属度函数;5)指标数据值作为输入,隶属度函数值作为指标量化值输出。
以命中能力的下层指标发射离轴角为例,首先该指标与武器命中能力相关,相关系数为-0.279,通过数理统计得到发射离轴角分布的直方图,如图4 所示。

图4 发射离轴角分布直方图Fig.4 Histogram of emission off-axis angle distribution
经过分布检验,离轴角的数据为伯努利分布,对指标值应用区间分位数最大相关系数算法[14],找到最大相关区间与最大无关区间。最大相关区间为(8°~32°),即与命中结果相关系数最大区间,此时相关系数为-0.286,最大无关区间为(0°~16°)。因此,指标值<8°与结果无关,确定为隶属度函数边界值,隶属度函数值为1,指标区间在(8°~16°)选择其概率密度函数作为隶属度函数,当指标值>16°时,指标值与命中能力指标相关系数最大,即离轴角越大命中能力越差,则隶属度函数趋近于0。在区间(8°~16°)的概率密度函数可近似为正态分布。由此,离轴角指标更新后的隶属度函数为:
由图5 可知,离轴角指标可以通过隶属度函数进行指标的量化,同理将其他量纲类指标进行量化处理,再与权重聚合后得到命中能力的效能值。对所有相关系数大于0.01 的16 个指标进行分布检验,其中,正态分布的10 个;几何分布4 个;伯努利分布1 个;指数分布1 个。将指标数据作为输入代入隶属度函数,输出指标量化值并带入到评估模型可验证该方法的有效性。
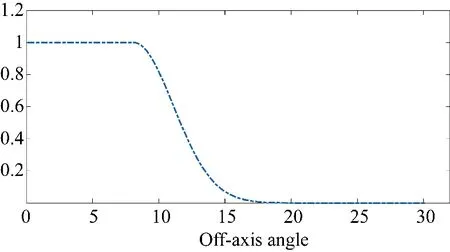
图5 离轴角指标的隶属度函数曲线Fig.5 Affiliation function curve of off-axis angle index
4.2.2 定量概率类指标的量化
主要采用代定函数法。例如:载机的被发现概率也就是敌方雷达发现概率,其表达式为:
式中,S/N 为雷达接收机输出信噪比;pf为虚警概率;erf(x)为误差函数,其表达式为:
4.2.3 定性概率类指标的量化
对于大多数的定性概率类评估指标,例如:载机抗毁能力、机动性能、隐身性能等,量化方法可采用吴志飞等提出的去模糊处理方法以及王睿等提出的基于专家可信度与区间值集结的定性指标量化方法[7,10]。
此外,本文将部分定性概率类指标转化为归一化之后的适应度函数,使其作为指标的量化值。以航迹规划质量性能指标量化为例。航迹规划是安全和高效完成飞行任务的基本要素,特别是对于战斗机,准确地规避雷达、地空导弹等危险源、地形障碍,可有效提升载机的突防能力。本文通过多约束条件下粒子群优化算法对已知航迹进行优化[15],将载机威胁、路径长度、油耗等多约束条件转化为适应度函数,属于成本型指标,极小值为最优。将适应度函数输出的最大值max(F)与最小值min(F)作为比较区间,并计算已知样本航迹的适应度值F1,归一化之后得到量化值表达式:
其中,F 为已知样本航迹的量化输出值∈(0,1),F越大说明已知航迹的质量越高。
4.3 指标的权重与聚合
4.3.1 机器学习算法确定量纲类指标权重
在制导与飞行控制段,武器的突防能力是确保命中的前提条件,命中能力可体现武器自身性能,通过分析飞行试验数据与遥测数据可以得到影响500 kg 激光制导炸弹命中结果的若干影响因素,如图6 所示。
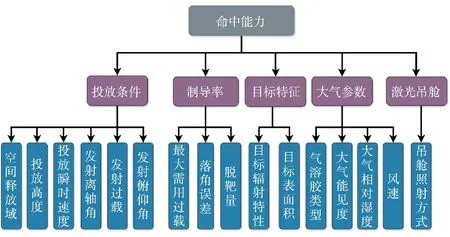
图6 激光制导炸弹命中能力指标的子类指标Fig.6 Subcategory indicators of laser-guided bomb hit capability indicators
通过数据预处理,影响激光制导炸弹命中能力的要素被分为5 类,16 个底层指标值可从数据中获得。因此,可将去量钢化的底层指标与命中结果(类标签)导入随机森林分类模型中,基于信息熵理论得到各属性的重要性即权重值。在Jupyter 环境下调用feature_importances 命令可直接得到各指标在该分类模型中的权重值。聚合后的命中能力PG1的表达式为:
式中,ω1i为影响命中能力指标的权重;Ci隶属度函数处理后的量化值。
同理可将比例距离转化为隶属度函数进行效能值的量化。在确定类标签时,基于建筑物理结构的完整性,借鉴俄陆军火力毁伤理论体系[11],将目标毁伤面积≥60%的样本标签值设为1,其他样本标签值设为0,利用随机森林模型对毁伤效能的5个指标的数据进行分类训练,与命中能力权重计算方法相同。聚合后的毁伤能力PD表达式为:
式中,ω5i为毁伤能力各指标的权重;Di为隶属度函数处理后量化值。
4.3.2 其他方法确定权重
1)专家评定法[16]:由N 个专家针抗毁能力、机动性能与隐身性能3 个因子进行打分,给出权重值来量化计算载机的生存能力。2)应用作战模拟法[17]:目标捕获概率可用作战模拟法,通过统计的飞行试验数据,得到飞机吊舱在执行任务时发现并且捕获到目标的次数n 与飞行总次数m 的比值n/m 作为吊舱的捕获概率。3)层析分析法:在评估指标体系中,可能会出现定量概率、定性概率指标以及量纲类指标在同一层级的问题,该问题可通过专家打分,用层次分析法构造判断矩阵并进行一致性检验,给出权重。
5 算例
初始条件如表1 所示,在可用度的计算上,由式(4)得到串联系统的可用度aC=0.967,导引与飞行控制系统可用度aG=0.987 6,引战系统的可用度aF=9 883,3 个阶段的可用度向量为:
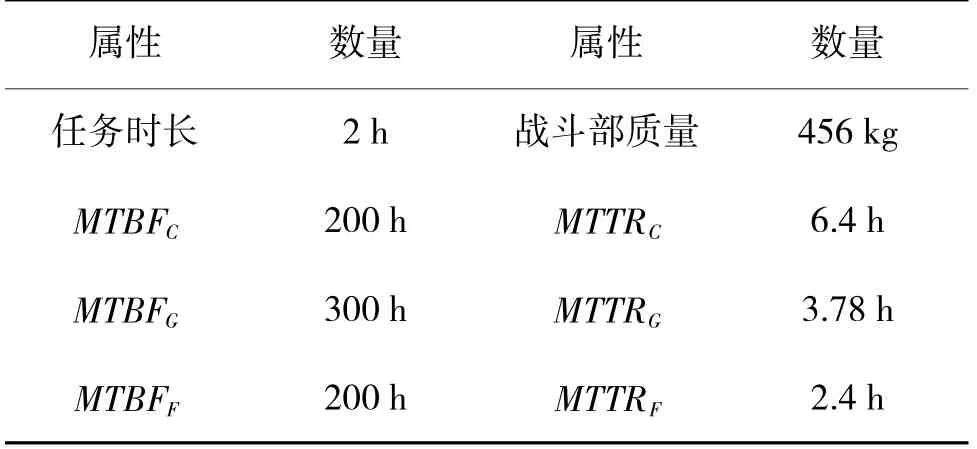
表1 评估初始条件Table 1 Initial conditions of assessment
其中,A1、A2、A3分别代表3 个阶段可用度向量,在可信性的计算上,通常制导武器各个系统的可用性成指数分布。已知任务时间T=2 h,则:
RC、RG、RF分别为3 个系统的可靠性,因此,3 个阶段的可靠性矩阵为:
如果以某个样本的效能值来评估武器的效能值过于片面,本文以20 组飞行试验数据样本作为参考,对激光制导炸弹武器系统进行评估。首先需要确定衡量标尺标度,比如优(0.85~1)、良(0.70~0.85)、中(0.60~0.70)、一般(0.40~0.60)、差(0.20~0.40)、劣(0~0.20)。数据样本代入式(10)、式(12)、式(13),各效能指标的权重见下页表2 所示,指标量化与权重聚合得到3 个阶段的能力矩阵C1、C2、C3,进而得到3 个阶段的评估结果。3 个任务阶段的权重通过层次分析法得:ε=(0.279 0.315 0.416),应用式(2)得到总体任务效能。由此得到20 组飞行数据样本的评估结果。
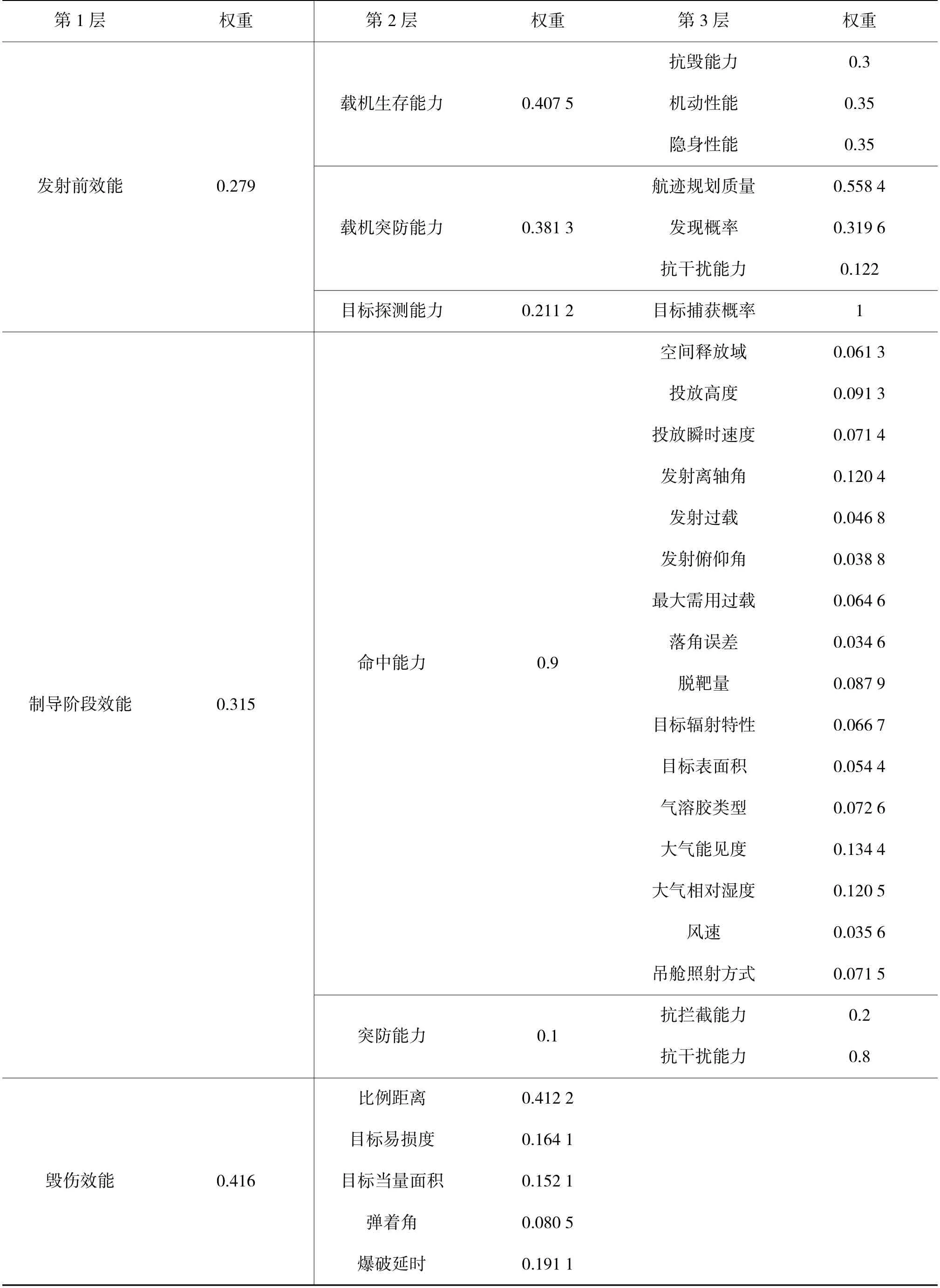
表2 激光制导炸弹指标权重表Table 2 Weighting table of laser-guided bomb indicators
第42 页表3 中所示,第1 阶段效能主要是评估载机的效能,该弹型的主要载机为二代半战机,各方面性能还略显不足,评估结果为一般;第2 阶段考察的是机- 弹协同能力与武器在战场环境中的适应能力,武器飞行制导阶段的效能评估结果介于良好与中,说明在机与武器协同能力有待提升,制导阶段受环境影响较大;第3 阶段的命中毁伤效能评估结果为优,说明武器具有很强的毁伤能力。而总体效能评估结果为良好,说明该弹型在整体作战流程中表现是不错的。通过分析获取的飞行试验数据与毁伤评估数据,比对后发现该系统效能的评估结果与实际吻合度较高,说明了模型的有效性和适用性。
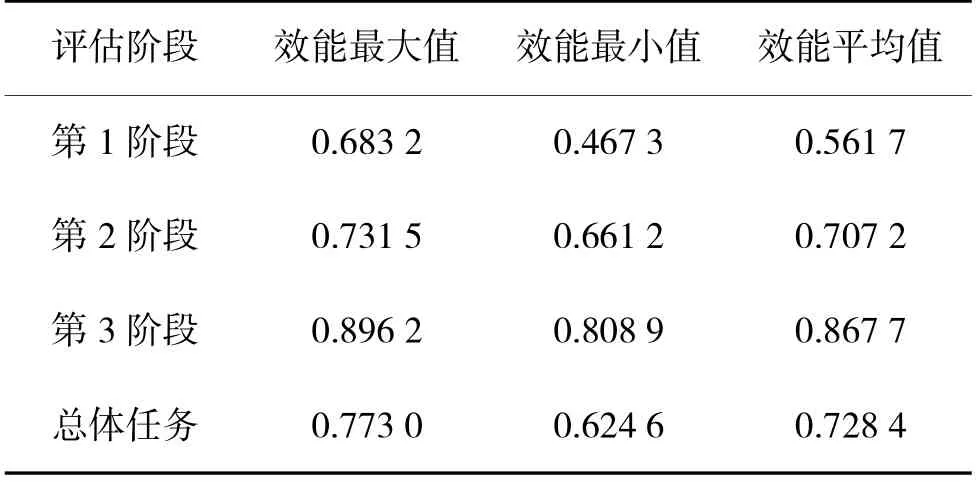
表3 阶段及总体任务评估结果Table 3 Assessment results of phase and overall mission
6 结论
为提升评估模型的准确性,针对多种效能指标选取适合的量化方法是十分必要的,针对量纲类指标,本文通过分析指标分布状态,提出了利用最大相关系数区间构建隶属度函数量化效能指标的新
方法;针对部分定性指标,应用粒子群智能优化算法构建适应度函数作为该指标量化值。在指标权重的计算方面,本文还应用机器学习算法确定了命中能力与毁伤能力各指标的权重。通过20 组典型试验数据的量化计算,得到了500 kg 激光制导炸弹3个阶段的效能值区间以及总体任务效能评估结果,该方法在效能值的量化与权重的计算方面均给出了新的思路,提升了评估模型的准确性,具有一定的应用价值。
