基于改进LADRC 的矢量推力双旋翼飞行器姿态控制*
2024-04-16蔡少泓院老虎赵维涛
蔡少泓,院老虎,赵维涛
(沈阳航空航天大学航空宇航学院,沈阳 110136)
0 引言
近年来,由于工业领域技术的变革,无人机得到迅速发展。四旋翼、六旋翼等多旋翼无人机因其易于操纵、起降场地简易等特点,被广泛应用于疫情防控、通信中继、国防工业、搜救和农业等方面[1-5],但此类飞行器推力方向单一,只能通过改变电机的转速来实现操纵。随着任务场景的复杂化,如在室内搜救等任务中,要求无人机在密闭狭窄的环境中搭载必要的设备执行任务,这对无人机的负载能力、机动性能和控制精度等提出了更高的要求,传统多旋翼的局限性在这种环境下逐渐显露,难以满足任务要求[6]。相较于传统的多旋翼,矢量双旋翼仅有两幅旋翼且结构更为紧凑。旋翼数量的减少降低了旋翼间气流的相互扰动,矢量推力使其具备更强的机动性能,并且在相同功耗下双旋翼飞行器的起飞重量比四旋翼有较大提升[7]。
双旋翼无人机的控制量包含两个旋翼的转速及其倾转角,需要完成空间内位置及姿态控制,是多输入多输出欠驱动系统。旋翼的倾转使系统耦合性更强,不确定性更大。此外,在复杂环境下工作时可能面临多种未知因素的干扰,这对双旋翼无人机可靠的姿态控制与抗干扰能力提出了更高的要求。国外学者针对双旋翼飞行器控制器的研究相对较早,已经应用了PID、LQR、反步法等算法设计飞行器的姿态控制器[8-9],但以上算法均未验证飞行器的抗扰能力。国内研究者ZHANG 等设计了PID 姿态控制器并进行飞行实验,但未验证在受到外部扰动时的稳定悬停能力[10];杨立本等设计了PID 位置控制和ADRC 姿态控制相结合的控制方法[6],通过仿真验证了该方法的可行性,但其需要整定的参数较多,不利于工程应用。
自抗扰控制由PID 算法发展而来,无需被控对象精确的数学模型,能够利用扩张状态观测器实时估计模型未建模部分和外部扰动并进行补偿,当控制对象遇到未知扰动或者参数发生变化时也能实现较好的控制效果,具有很强的鲁棒性[11]。考虑到双旋翼飞行器的飞行特性且飞行中可能遇到未知扰动,本文利用改进LESO 提高对控制对象总扰动的估计和补偿能力,引入模糊控制简化参数整定并提高系统的跟踪速度,仿真结果表明本文方法具有较好的抗扰能力,具备一定可行性。
1 建立数学模型
双旋翼飞行器通过改变两幅旋翼的推力及其偏转角度实现对飞行器的位置和姿态控制。其中,同时改变两幅旋翼的转速实现飞行高度变化;左右旋翼差速旋转可实现飞行器的滚转运动;左右旋翼同向偏转可实现俯仰运动,同时向相反方向偏转可实现偏航运动。
定义机体坐标系为OBXBYBZB和地面坐标系为ODXDYDZD。从机体坐标系到地面坐标系的转换矩阵为:
式中,θ,φ,ψ 分别代表飞行器的俯仰角、滚转角和偏航角。
机体坐标系下的角速度和欧拉角微分的关系:
为方便建模引入以下假设:1)假定横列双旋翼飞行器是均匀对称的刚体;2)飞行器质心与几何中心重合;3)忽略旋翼倾转对重心的影响。根据牛顿欧拉方程可得:
式中,L,H 分别为旋翼中心到机体坐标系原点的水平距离和垂直距离;a1,a2是左右旋翼的偏转角度;T1,T2为分别为左右旋翼的拉力。
在地面坐标系下机体的位置和速度公式如下所示:
飞行器的力矩控制角运动,平衡状态下,忽略其左右旋翼的反扭矩和陀螺力矩的影响。在无外部扰动情况下,由式(5)可得飞行器的动力学模型:
式中,U1为旋翼的总推力控制量,U2,U3,U4分别为滚转、俯仰、偏航的控制量。
2 控制器设计
由数学模型可知飞行器的3 个姿态间存在耦合,此外,无人机在实际飞行中存在很多未知因素,这些扰动难以建立精确的模型,对无人机的姿态控制产生较大影响,不利于基于模型的控制方法。传统的自抗扰控制方法虽然具有高精度和高反馈效率等优点,但其参数太多,参数校正繁琐,不利于在工程中应用。高志强等提出了LADRC,对ADRC 进行线性化改造,将扩张状态观测器的参数与观测器带宽联系,线性化为LESO[12];采用一个PD 控制组合,将比例系数、微分时间常数和控制器带宽联系。线性化后的LADRC 具有控制性能优异,控制器参数少,物理意义明确,参数设置工作量小等优点,非常便于理论分析,能够满足工程应用的需要。
无人机的3 个姿态通道间相互耦合,可将其视为系统的内部扰动,根据自抗扰控制原理,姿态运动模型可改写为以下形式[13]:
式中,fi为系统的内部扰动;ωi为外部扰动;bi为补偿参数(i=2,3,4)。
本文以俯仰通道为例设计控制器,系统的内扰和外扰构成了系统的总扰动,可视为系统的扩张状态变量,通过线性扩张状态观测器进行观测。令其中,x3可导,则俯仰通道的模型可表示为:
式中,x1,x2,x3分别代表俯仰角、俯仰角速度及俯仰通道的总扰动。
传统的LESO 的设计如下:
式中,z1,z2,z3为x1,x2,x3所对应的观测值;β1,β2,β3为其观测值增益。
传统LESO 是通过z1和x1的误差e 来控制z1,z2,z3。z1,z2,z3依次逼近x1,x2,x3,这个顺序错乱系统则会失效。在该调节机制下,在z1跟踪x1到稳态之前对z2和z3的控制意义不大。当z1跟踪x1到达稳态后,e 的值已经非常小,此时需要选取较大的β2,β3来实现调节z2,z3,造成观测器性能下降。
由式(9)可得:
整理可得基于偏差控制原理的改进型LESO 如下,文献[14]已证明其稳定性,本文不再赘述。
线性反馈控制律及补偿部分如下:
式中,kp,kd为控制器增益。控制器需要整定的参数有β1,β2,β3,kp,kd,根据文献[12]可知:
将模糊控制原理引入LADRC,对PD 的参数进行在线调整以增强其控制性能和抗干扰能力。根据经验建立ωc的模糊规则,模糊规则如表1 所示。e、ec 为期望位置和当前位置间的误差及其变化率,输出为ωc,采用三角隶属度函数,模糊推理采用Mamdani 型。ωc的参数可以表示为:
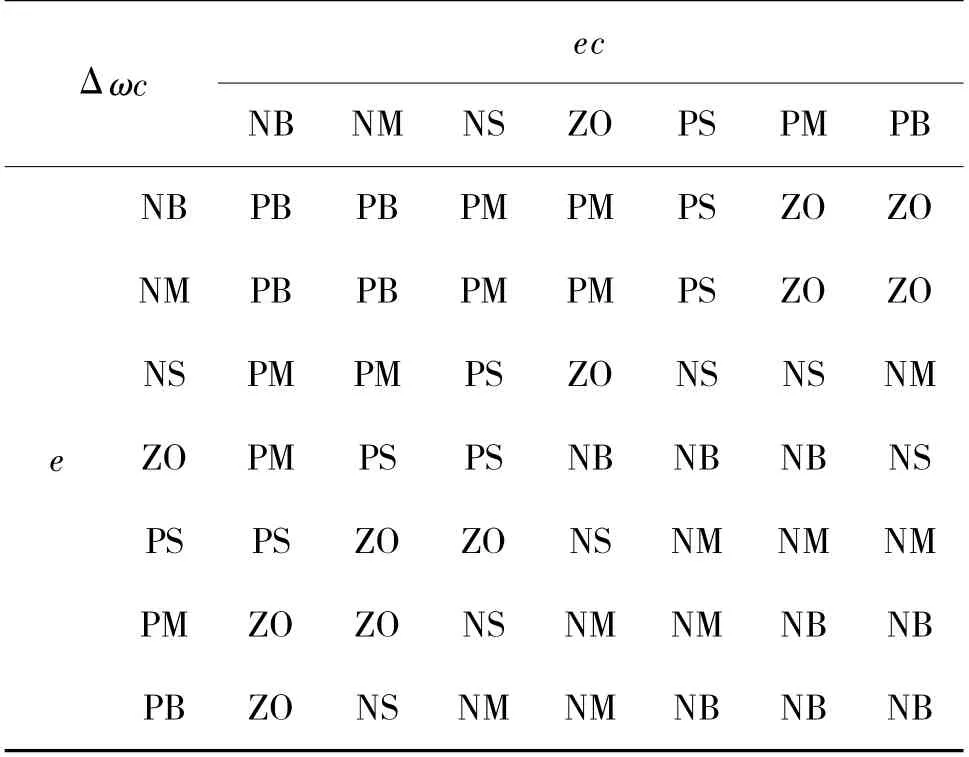
表1 Δωc 模糊规则Table 1 Δωc fuzzy rules
本文的控制方法主要由线性状态误差反馈控制律、改进型线性扩展状态观测器和模糊控制器组成。其中,改进LESO 作为控制器的核心部分,起到观测和估计扰动的作用[15],本文方法设计的姿态控制器结构如图3 所示。
3 仿真验证
通过Matlab/Simulink 验证本文所设计的双旋翼飞行器姿态控制器的性能,双旋翼飞行器的参数如表2 所示。
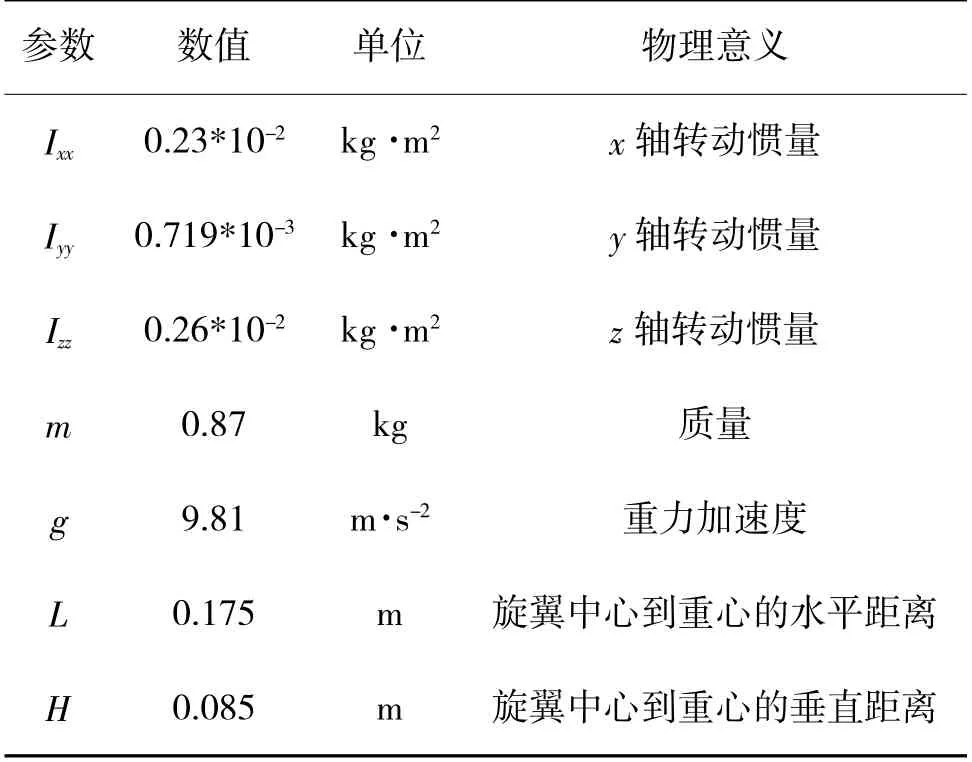
表2 双旋翼飞行器模型参数Table 2 Model parameters of dual-rotor aircrafts
将本文控制方法与传统的LADRC 控制器以及PID 控制器做对比。在无外扰动的情况下,仿真结果如图4 和图5 所示。图4 中,设置仿真时长为10 s。从图中可知PID 控制器超调量为8.9%,收敛时间最长。而本文方法,LADRC 无超调,均能较好地收敛且本文方法收敛时间最短。当控制量变化时,本文方法的控制效果最好。从图5 可以看出,本文的控制方法可以很好地跟踪输入的期望值,并且在跟踪过程中3 个姿态角的变化互不影响。
给定俯仰角的初始值θ0=0°,设其期望俯仰角θd=3°。加入图6 所示的脉冲扰动,仿真结果如图7所示。
分析表3 中俯仰通道各参数可知,在受到脉冲干扰时,本文方法的摆动幅度比传统LADRC 减少73.1%,比PID 减少76.5%;调节时间则分别缩短了49.8%及89.9%。
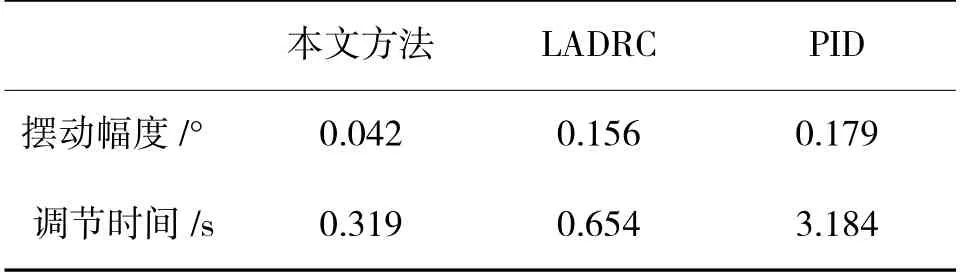
表3 脉冲扰动下俯仰通道参数Table 3 Pitch channel parameters under pulse disturbances
在t=[2,5]时加入图8 所示的随机干扰信号,仿真结果表明PID 和LADRC 控制方法的跟踪曲线波动较大,且PID 调节时间较长,而本文方法可以对扰动进行有效的抑制。根据俯仰角控制误差曲线图可知,在扰动区间内,本文所设计的控制方法对扰动的抑制效果更好,控制误差最小。
图11 显示本文算法和传统LADRC 对俯仰通道总扰动的估计情况,由图可以得出传统线性LADRC 对扰动的估计存在滞后,而本文方法能够实时估计俯仰通道的总扰动且精度明显高于传统LADRC。表明其比本文另外两种控制方法具有更好的抗扰能力。
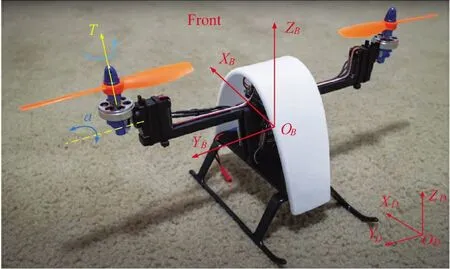
图1 机体坐标系和惯性坐标系Fig.1 Body coordinate system and inertial coordinate system
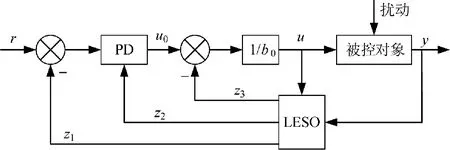
图2 LADRC 基本结构图Fig.2 Basic structure diagram of LADRC
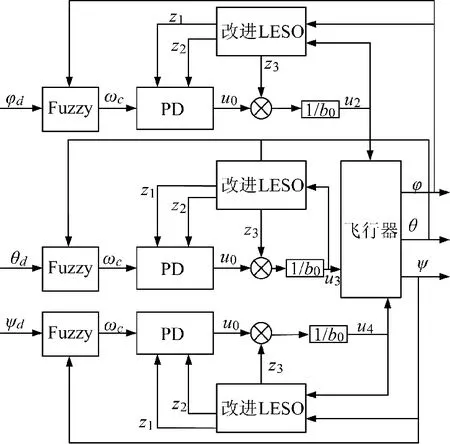
图3 姿态控制结构图Fig.3 Structure diagram of attitude control

图4 无外扰动时俯仰通道响应曲线Fig.4 Pitch channel response curve without external disturbances
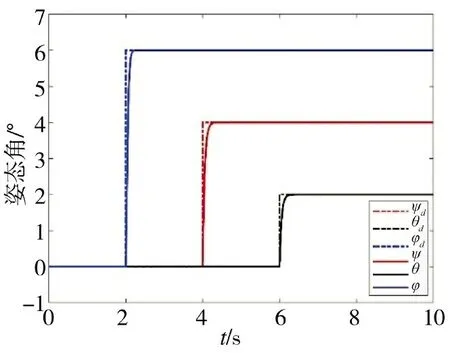
图5 本文方法的3 个姿态通道响应曲线Fig.5 Three attitude channel response curves of the proposed method

图6 脉冲干扰信号Fig.6 Pulse jamming signals
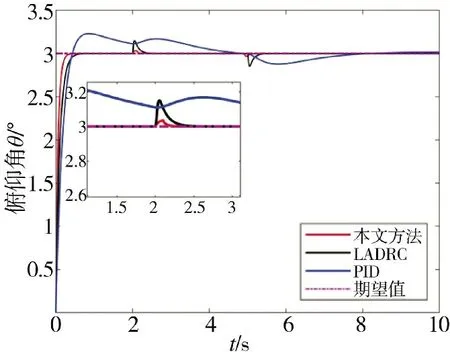
图7 脉冲扰动下俯仰通道响应曲线Fig.7 Pitch channel response curve under pulse disturbances
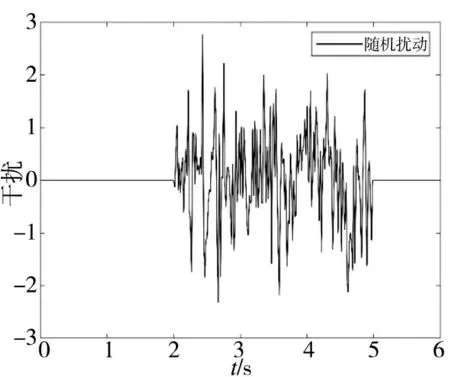
图8 随机扰动信号Fig.8 Random disturbance signals
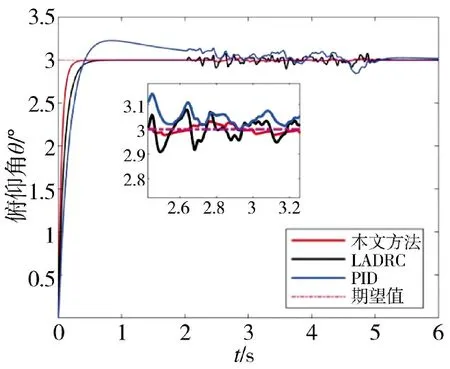
图9 随机扰动下俯仰通道响应曲线Fig.9 Response curve of pitch channel under random disturbances
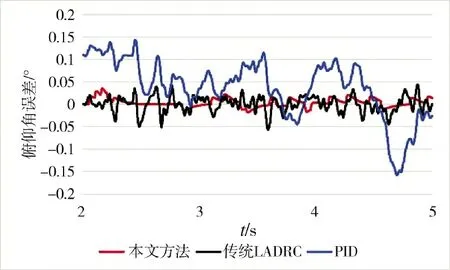
图10 俯仰角控制误差曲线Fig.10 Pitch angle control error curves
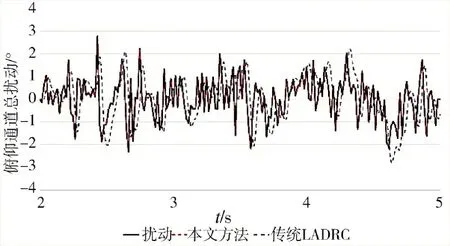
图11 俯仰通道总扰动及估计曲线Fig.11 Total disturbance and estimated curve of pitch channel
4 结论
本文针对矢量推力双旋翼飞行器耦合性强、模型建立不精确的控制问题,提出一种改进LADRC的姿态控制器。通过仿真验证了该控制器能够实时、精确的估计系统的耦合性及复合扰动,具有较强的抗干扰能力,模糊思想的引入进一步简化了参数的整定难度,相较于本文其他两种算法具有一定优越性,更适合工程领域的应用。
