改进的自适应扩展卡尔曼滤波雷达目标跟踪算法*

杨遵立，张 衡，吕 伟，余 娟，张从胜

（空军预警学院，武汉 430019）

0 引言

雷达目标跟踪是雷达数据处理中非常关键的一环，依据获取的雷达目标点迹，进行航迹起始、关联、滤波以及预测处理，实现对目标运动的实时跟踪［1-2］。标准卡尔曼滤波算法是在状态空间上的线性高斯滤波算法［3］，在雷达目标跟踪理论研究中得到广泛关注［4］。当机动目标出现非线性运动场景时，目标真实状态与滤波模型不匹配，卡尔曼滤波算法会出现跟踪精度下降，出现滤波发散甚至跟踪丢失的问题。因此，国内外学者进行研究提出了一些改进算法，其中有代表性的是扩展卡尔曼滤波（EKF）算法［5-6］。

EKF 算法对非线性系统滤波函数进行泰勒一阶线性展开式并忽略高阶项，将非线性系统模型转化为一个近似线性模型，从而对卡尔曼滤波算法进行修正［6］。该方法简单计算量小，可较好对线性、非线性机动目标运动状态进行预测跟踪。文献［7］中提出一种改进EKF 算法，通过实时计算新息方差自适应调整滤波增益，从而进行目标跟踪。

在非线性目标场景中，当系统运动模型与噪声模型失配，系统积累误差较大时，EKF 滤波算法也存在滤波效果不佳或出现滤波发散。反向传播（BP）神经网络能够自适应学习，具备良好的非线性映射能力，广泛应用于雷达数据处理场景中［8-9］，本文采用BP 神经网络对EKF 算法进行自适应修正，同时，根据噪声情况，引入可调更新因子，采用位置误差最小化的优化模型自适应地对预测位置信息进行二次优化，从而提高目标位置跟踪精度和稳定度。

1 EKF 和BP 神经网络算法原理

1.1 EKF 滤波算法原理

常用的雷达目标运动模型有匀速模型（CV）和匀加速模型（CA），本文以该两种模型为例考虑目标跟踪场景，1 个目标进行匀加速运动，另外1 个目标进行匀速运动。匀速或匀加速直线运动目标状态方程和测量方程可表示如下［1］：

其中，X（k）为k 时刻的目标状态；F 为状态转移矩阵；G 为过程噪声分布矩阵；Z（k）为测量矩阵；H 为观测矩阵，v（k）和w（k）分别是系统的过程噪声和测量噪声，两个噪声相互独立且服从均值为0 的高斯分布，方差分别为Q 和R，T 为系统采样间隔。

式（2）中测量矩阵Z（k）表示如下：

其中，（x0，y0）为观测点的坐标。

EKF 滤波使用展开一阶泰勒级数进行近似，从而近似变换为线性系统进行滤波处理。EKF 滤波基本公式如下［7］：

观测矩阵H 为非线性函数h（X（k））的一阶泰勒的雅克比矩阵，表示如下：

k+1 时刻新息u（k+1）、滤波增益K（k+1）和协方差矩阵P（k+1|k+1）更新为：

文献［7］中噪声方差R 随时间分段变化，在长度L 连续区间内可得改进滤波增益为：

上述这些公式完成了EKF 滤波更新过程，只要给定状态初始值和协方差初始值P（1|1），即可进行全部时刻迭代估计。

1.2 BP 神经网络算法原理

BP 神经网络学习过程分信号正向传递和误差逆向传递过程。以3 层的BP 神经网络为例，设各层参数分别为：输入层中输入x，神经元个数m；隐含层中输出a，神经元个数s，激活函数f1；输出层中输出o，期望输出ϑ，神经元个数n，激活函数f2［8-9］。

隐含层第i 个神经元输出ai，输出层第k 个神经元的输出ok，表示如下：

BP 神经网络输出误差定义如下：

经过信息正向传递可以求出输出值，当误差满足精度要求时，结束学习；不满足精度要求时，便通过逆向传播误差值，不断调整权值ω，使误差E 达到最小。设η 是神经网络学习率，调整后权重值和如下：

2 改进自适应EKF 滤波算法

2.1 BP 神经网络自适应修正EKF 滤波

当系统运动模型与噪声模型失配，系统积累误差较大时，EKF 滤波算法也存在滤波效果不佳或出现滤波发散。由于BP 神经网络能够自适应学习，具备良好的非线性映射能力［8-9］，本文采用BP 神经网络来辅助修正扩展卡尔曼滤波的结果，减小EKF 滤波误差，从而提高运动目标跟踪精度。

本文构建了3 层BP 神经网络，包括输入层、隐含层和输出层，如图1 所示。采用的BP 神经网络结构中，输入层参数包括更新信息，EKF 预测参数，滤波增益K（k+1），测量参数Z（k+1），输出层节点为输出预测的位置信息。隐含层节点数对BP 神经网络性能影响巨大，隐含层节点数增多可提高网络性能，但也会延长训练时间，隐含层节点数用式（19）确定：

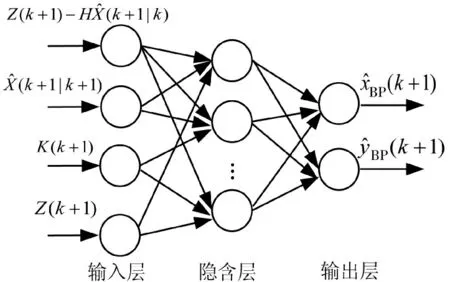
图1 BP 神经网络结构Fig.1 BP neural network architecture

式中，M 和N 分别为输入层和输出层节点数；a 是［0，10］之间的常数。

BP 神经网络，给定误差函数e，设定最大学习次数P 与精度ε，选用Tan-Sigmoid、log-sigmoid、线性purelin 函数分别为输入层、隐含层和输出层传递函数，采用L-M 算法进行训练，反复训练使得网络均方误差最小。

测量值Z（k+1）在绝对坐标系下x 和y 轴的测量信息分量xZ（k+1）和yZ（k+1）分别为：

其中，ρ（k+1）和θ（k+1）分别为k+1 时刻测量值Z（k+1）在极坐标下的长度和角度分量，其中，

依据目标运动规律，目标位置存在一定的偏差范围，不论是EKF 算法还是BP 神经网络算法的一些预测值可能存在较大偏差，需要对其进行一定的修正，这里假设在绝对坐标系下系统最大的偏差范围为δ，以测量位置信息为基准，k+1 时刻EKF 预测坐标和满足如下条件：

不满足式（19）按如下进行更新修正：

类似的，以修正后的EKF 预测值为基准，BP 神经网络预测值也满足如下条件：

2.2 优化模型自适应选择最佳预测信息

BP 神经网络算法是一种局部最优算法，结果可能不最优的，需要确定最优的预测位置结果。一种基于实际噪声情况可调更新因子，类似动态杂波图的方式自适应产生该更新因子，可根据噪声情况自适应获得，用于EKF 和BP 神经网络映射的位置预测值的加权处理，处理结果可提供进行最优化选择。

k+1 时刻，EKF 预测和测量值的第1 综合加权值坐标，表示如下：

BP 神经网络映射预测和EKF 预测第2 综合加权值坐标表示如下：

为了获得最佳的位置预测信息，本文基于误差最小化的优化模型，从上述EKF 预测值、BP 神经网络预测值以及加权值中，自适应获得最优位置预测信息和。从这4 个预测值中自适应选择最优值；从这4 个预测值中自适应选择最优值，优化模型表示如下：

本文所提算法如算法1 和图2 所示。

images/BZ_25_1288_427_1947_464.pngS0：初始值images/BZ_25_1454_523_1551_565.png，P（1）且k=1，判断运动模型是CA 还是CV，确定对应F 和G S1：计算images/BZ_25_1418_646_1854_692.pngS2：更新k+1 时刻协方差P（k+1|k+1）和EKF 位置预测信息images/BZ_25_1343_772_1547_817.pngS3：确保S2 中的images/BZ_25_1548_839_1849_884.png满足式（21）条件，不满足按照式（22）进行更新，得到k+1 时刻修正后的EKF 位置预测信息S4：基于images/BZ_25_1413_1024_2188_1078.png，用BP 神经网络映射得到预测位置信息，images/BZ_25_1935_1100_2218_1146.pngS5：确保S4 中BP 预测信息images/BZ_25_1725_1168_1997_1213.png满足式（23），不满足则对该值以S3 修正后images/BZ_25_1768_1235_2059_1279.png在δ 范围内进行修正S6：用更新因子α，β，γ 按照式（24）～式（26）计算修正后EKF预测值和BP 神经网络映射值以及测量值构成的3 个综合加权值S7：按照最优化模型式（27）～式（28）分别获取最优化的位置预测信息images/BZ_25_1492_1596_1635_1640.png和images/BZ_25_1672_1596_1807_1640.pngS8：将k+1 赋值给k，重复算法S1～S8 继续获得下一个时刻最优化位置预测信息，直到k 达到跟踪次数上限，停止算法

图2 本文提出算法的流程图Fig.2 The flow chart of the proposed algorithm

3 仿真分析

基于CA 和CV 运动模型二维平面坐标，通过仿真实现本文基于BP 神经网络修正和优化的自适应扩展卡尔曼滤波算法，其中，噪声参数设定是一个变化范围，分噪声干扰大和干扰小的场景。仿真参数如表1 所示。

图3 和图4 是在噪声干扰较大时CA 和CV 模型下，仿真出的本算法预测的目标在X 和Y 轴轨迹曲线，前8 个点文献［7］的EKF 预测作为BP 神经网络输入，从第9 个点才是所提自适应BP-EKF 预测修正值。在干扰噪声较大场景下，不论CA 还是CV 场景，本算法对文献［7］中改进EKF 算法有一定性能提升，可比较准确进行机动目标位置预测。

图3 噪声干扰较大时，CA 场景预测轨迹曲线Fig.3 Prediction trajectory curve in CA scene with stronger noise interference

图4 噪声干扰较大时，CV 场景预测轨迹曲线Fig.4 Prediction trajectory curve in CV scene with stronger noise interference

图5 和图6 是在噪声干扰较小时，CA 和CV模型下仿真出的预测目标轨迹曲线，此时本算法预测与文献［7］中算法结果相近，都可较好地进行目标位置预测，佐证本算法是在噪声较大，与系统模型不匹配场景下，可对目标位置信息的预测有较好的改善。

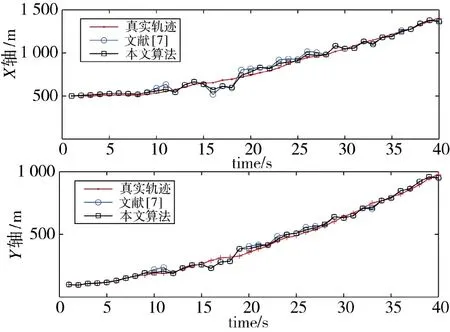
图5 噪声较小时，CA 模型预测轨迹曲线Fig.5 Prediction trajectory curve of CA model with weaker noise interference

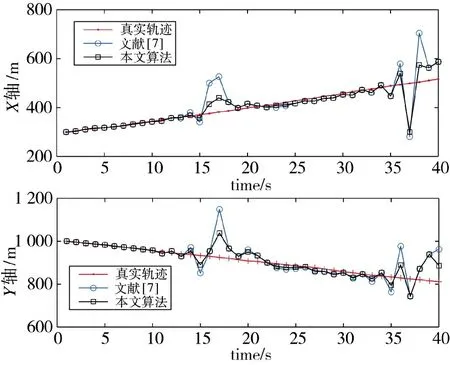
图6 噪声较小时，CV 模型预测轨迹曲线Fig.6 Prediction trajectory curve of CV model with weaker noise interference

目标跟踪精度衡量的标准是均方根误差RMSE，设M 为蒙特卡罗仿真次数，Rx（k）和Ry（k）为x 轴和y 轴在k 时刻的均方根误差，xi（k）和yi（k）为第i 次蒙泰卡罗仿真目标在k 时刻x 轴和y 轴位置真实值，和分别为第i 次蒙泰卡罗仿真目标在k 时刻x 轴和y 轴的预测值。RMSE 表示如下：

图7 和图8 分别为CA 和CV 模型下噪声干扰较大时，仿真的均方根误差RMSE 曲线图，经过50次蒙泰卡罗仿真，可看到本算法比文献［7］中改进EKF 算法均方根误差低很多，滤波误差精度和稳定度得到提升。

图7 CA 模型下预测的滤波误差曲线Fig.7 Filter error curve of CA model

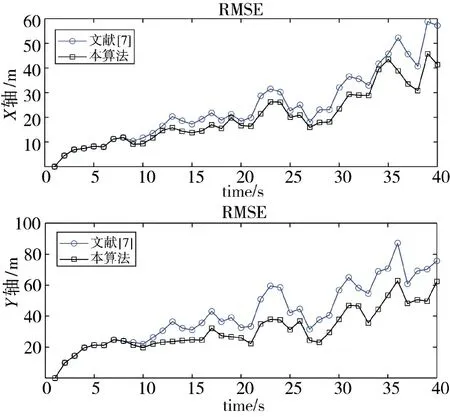
图8 CV 模型下预测的滤波误差曲线Fig.8 Filter error curve of CV model

4 结论

本文提出了一种基于BP 神经网络修正和优化的自适应的EKF 算法进行雷达目标跟踪，根据噪声影响情况，使用可调更新因子进EKF 预测位置信息、测量信息和BP-EKF 预测信息值的权重处理，并基于优化模型选择最优的位置预测信息。仿真分析表明，本算法可以减小滤波目标跟踪预测的误差，提高目标跟踪的滤波精度和稳定度。