基于射击时机的坦克射击门分析及改进*

张贤椿，姚志军，王 军，刘宗凯

（1.南京理工大学自动化学院，南京 210094；2.白城兵器试验中心，吉林 白城 137001）

0 引言

坦克身管作为弹丸的最后投射装置，在发射条件、气象条件确定的情况下，弹丸出膛瞬间身管的运动状态直接决定了弹丸的外弹道轨迹和落点。改进坦克生产制造工艺、火控以及炮控性能可优化身管的动态特性并提升坦克的瞄准精度，是提升坦克行进间射击精度的主动措施。而在坦克性能确定的前提下，增加对身管振动状态下对有效射击时机的实时判断能力，如引入射击门体制，是提升坦克的命中精度的被动措施。

传统射击门是指以火控计算机输出的射击诸元为基准的射击线角度容许误差区域，基于身管角度误差阈值的开火判据称为简单射击门［1-3］。坦克采取射击门体制的底层逻辑是：在坦克静止或低速情况下，射击门与目标截面存在较为确定的“映射”关系，即身管在射击门内开火大概率可确保弹丸命中目标，这一提升坦克射击精度的被动措施在实际射击中亦得到体现。然而随着坦克在实际路面行进速度的提高，坦克高速行进的可射击时机和命中概率下降显著［4-5］。坦克射击门是决定射击时机的关键环节，故有必要针对坦克射击门对射击时机的影响进行分析，以提升坦克在高速行进间的命中概率。本文通过对已有多种射击门的机理进行分析，指出现有射击门在射击时机判断上的不足之处，并给出了射击门的改进方法，可使坦克火控最大限度地把握已有的射击时机。

1 射击门体制

身管运动基于射击门向目标射击时的弹丸落点关系如图1 所示，在射击门的作用下，弹丸基于身管炮口端运动曲线g 点飞向目标截面W 所属平面S 的落点Q，Q 点在W 面上运动形成的曲线s 的映射关系如图1 所示。这里定义身管在高低向的完整穿越过程，为身管从射击门一侧穿入并从射击门另一侧穿出的过程，理论上身管对射击门的穿越性对应着弹丸落点Q 对目标截面的穿越性。

图1 基于射击门的弹目交汇图Fig.1 Projectile and target intersection diagram based on firing gate

坦克高速行进间射击精度的显著下降，其主要原因是坦克身管振动强度增大对发射的弹丸落点影响偏差变得不可忽略，主要体现在两个方面：1）弹丸从开火到出膛的击发时延导致出膛时的身管角度偏出射击门［6］；2）在弹丸出膛瞬间身管运动赋予弹丸的切向速度导致弹丸飞行轨迹偏离目标截面［7-8］。针对这两种情况，文献［6-7］分别给出了针对弹丸膛内运动时延和身管运动切向速度的射击门改进方法。图2 分别给出了简单射击门、考虑击发延迟的射击门（简称延迟射击门）以及考虑身管切向速度的射击门（简称速度射击门）的控制逻辑。

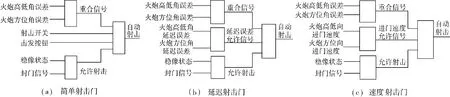
图2 不同射击门控制逻辑Fig.2 Control logic of different firing gates

以上射击门控制逻辑中，图2 除了要求的射击开关、击发状态、稳炮状态和封门信号等使能信号外，其射击门控制逻辑的主要数学模型如下描述。下面分别对图2 所示的射击门的数学控制逻辑进行分析。

1.1 简单射击门

简单射击门是以射击诸元高低和方位角度为基准，实际火炮身管角度与射击诸元角度的误差允许区间，满足简单射击门的判据逻辑为：身管处于射击门内时击发即可命中目标。表达式为：

式中，Mθ与Mφ表示方位及高低向的误差门限值，θ（t）与φ（t）表示火炮动态高低角及方位角，θ0与φ0火炮高低向与方位向装定诸元角度，该射击门仅对身管瞬时角度设置了门限值，对身管振动角速度未作约束。

1.2 延迟射击门

由于自坦克击发到弹丸出膛的击发时延ΔT的存在，ΔT 通常在10 ms 左右，可以近似认为身管在ΔT 时间内的角速度不变，则考虑击发延迟的射击门判据逻辑为：在身管进入简单射击门的前提下（自动击发底火），因击发延迟导致的身管角度依然处于射击门内。表达式如式（3），其复合射击门控制逻辑为［6］：

其中，式（3）中ωθ为高低角速度，ωφ为方位角速度。对应的身管运动角速度约束如下：

1.3 速度射击门

坦克行进间火炮身管振动赋予弹丸切向速度影响弹丸落点，且其落点偏差量与弹丸飞行时间近似呈线性关系［8］，通过简化计算落点偏差，确定射击门的开火逻辑为：自火炮身管在一侧进门时自动击发底火，弹丸因切向速度及击发时延引起的落弹偏差依然在目标着弹面内，可得约束身管运动的角速度如式（6），其复合射击门控制逻辑为［7］：

其中

且

分别为高低向和方位向的弹丸落点偏差，可知弹丸落点偏差方向与身管运动方向保持一致。上式Rgd、Rfw分别为身管高低向和方位向的回转半径，B、H 分别为炮目视角下目标的长度和宽度，D 为炮目距离，v 为弹丸出膛时的合速度。

以上不同射击门的条件可区分为身管角度条件和角速度条件，其中式（1）、式（2）和式（5）为身管角度条件，式（4）和式（6）为身管角速度条件。由上可知，无论是延迟射击门还是速度射击门，其判断射击时机的核心逻辑是：身管须处于简单射击门内，同时要求身管角速度足够小，以确保击发时延ΔT 过后的身管继续处于射击门内。下面通过分析身管高低角穿越射击门过程中的开火时机，来阐明现有射击门在射击时机的把握上存在的缺陷。

2 射击时机分析

以身管的高低向运动情况为例，身管从A 到B 一次单向运动过程，形成对高低向误差门限值［-Mθ，Mθ］的完整向下穿越，如图3 左侧所示；其身管角速度变化如图3 右侧所示。针对以上射击门的控制逻辑，可知无论火炮采取哪一种射击门体制，火炮必须在t1（对应s1位置）时刻（含）后的简单射击门阈值［-Mθ，Mθ］范围内击发。

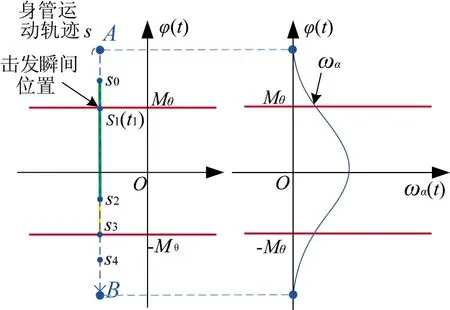
图3 高低向上射击时机示意图Fig.3 Schematic diagram of firing opportunity in elevation direction

由于弹丸落点会基于身管运动方向偏移，式（8）在身管振动速度较快时，其在射击时机的判断上存在以下两个问题：

一是部分在简单射击门外的身管位置也是有效的射击时机，由于简单射击门的角度约束导致该部分射击时机无效，如图3 中s0s1线段所示；

二是部分在简单射击门范围内的开火时机为无效射击时机，却被已有射击门当成有效射击时机，如图3 中s2s3线段所示。

同时，由于延迟门及速度门均设置了角速度的约束条件，坦克行进速度增加使得身管振动速度过大时，会导致身管在完全穿越情况下也没有射击时机。然而从原理上分析，无论身管振动速度多大，对于身管的一次完全穿越过程，如图3 中身管高低向从A 到B 点的运动过程，其对应的弹丸落点轨迹s（见图1）亦对目标截面形成穿越（方位向同理），存在有效射击时机，只要火炮的击发时刻控制合理即可。

由以上分析可知，现有的射击门均存在对有效射击时机判断不准确或错失射击时机的情况，为更好地把握可能的射击时机，本文提出了一种射击时机快速预测机制下的射击门改进方法。

3 射击时机预测模型

记身管t 时刻运动状态向量

状态向量中各分量分别为身管高低及方位的角位置、角速度和角加速度。坦克身管的运动状态可通过在身管上加装传感器的方式并进行相关的数据处理得到［10］。身管在预测时长Δt 后的高低及方位向的预测角度可表达为

影响弹丸外弹道飞行轨迹的身管运动状态参数有身管角度和角速度，加速度对弹丸落点不产生直接影响［11］。由于击发时延Δt 非常短，可认为身管角速度在Δt 内保持不变，则身管角速度影响弹目偏差近似表达如下［6］：

其中，ΔB（t）与ΔH（t）为弹丸落点在目标截面高低及方位向上相对射击诸元对应理想落点的偏差，v表示弹丸出膛时的平均飞行速度。对于坦克炮这类低伸弹道，该弹目偏差对应的身管指向角偏差亦可近似表达为

将击发时延Δt 后的预测角度θ（t+Δt）、φ（t+Δt）考虑进来，则

相当于火炮在考虑击发时延和身管切向速度影响下的对等静态开火角度。这样可基于式（13）中的身管预测角度和的计算结果，以简单射击门为身管预测角度的“目标区域”，动态判断坦克火炮的开火时机，即满足

由此给出具备身管运动预测能力的射击门控制逻辑如图4 所示，图中给出的射击门控制逻辑与传统的简单射击门控制逻辑类似，仅在简单射击门前端增加了身管运动状态的预测模型，即引入的判断变量由原来的身管当前角度替代为角度预测值，该预测值已将击发时延和身管切向速度的影响考虑在内，且无需考虑身管须处于简单射击门内的角度约束。

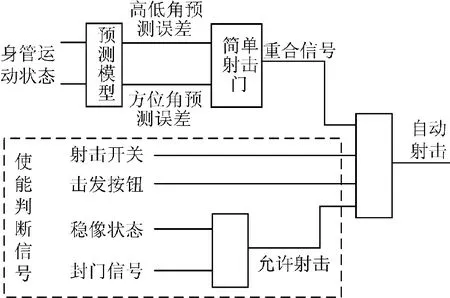
图4 基于预测模型的射击门控制逻辑Fig.4 Control logic of firing gate based on the prediction model

需指出，本文对身管在击发时延内的运动过程做了简化，仅采用了较为简单的线性预测模型描述击发时延内的身管运动过程，这是现有改进射击门的通用做法［2，7］，该简化处理不会对改进射击门模型在射击时机判断上造成显著影响。受篇幅和本文研究方向所限，身管运动预测模型可单独研究，新的预测模型可替换图4 中的对应模块，亦对该射击门的整体控制逻辑不产生影响。

4 数值仿真分析

为验证预测机制射击门在射击时机把握上的合理性，本文通过坦克动力学模型在路面谱激励下实现身管振动特性的仿真，采取数值分析法对以上各种射击门决定的射击时机进行计算和对比分析，验证本射击门在射击时机把握上的优越性。

4.1 坦克系统动力学建模简介

坦克武器系统主要由坦克底盘和炮塔火炮组成。其中，坦克底盘由车体、车体左右两侧的履带、车体两侧的多个负重轮，以及连接履带和负重轮的悬挂装置组成，悬挂装置包括减震器、弹性装置等器件。炮塔火炮部分包括炮塔（含座圈）、火炮身管、炮塔轴承装置、火炮耳轴起落装置等，炮塔在座圈回转平面内相对于坦克底盘做方位旋转运动，火炮身管在耳轴回转平面绕耳轴做俯仰运动。

为简化分析，作如下假设：

1）车体视为刚体，其载荷和负重轮简化为集中质量和弹簧、阻尼的组合，悬挂装置简化为弹簧、阻尼的组合；地面激励输入为点输入，忽略因平衡肘摆动造成的输入点与车体相对位置的变化，忽略因角振动引起的负重轮相对于车体的位置变化，仿真运算时不考虑车辆的结构振动。

2）火炮系统各部件均视为刚体，不考虑身管、炮尾、摇架之间存在的间隙，以及身管的弯曲变形。

根据以上假设，坦克系统建立下页图5 所示的受力结构。

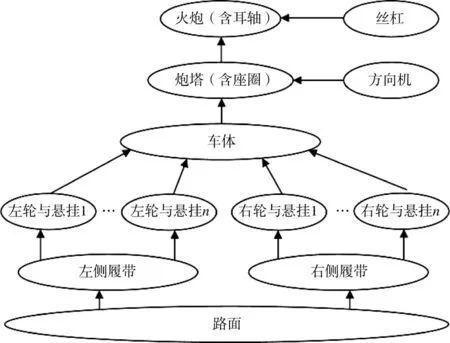
图5 路面-车体-火炮系统受力结构图Fig.5 Stressed structure diagram of road-vehicle-artillery system

通过建立图5 所示的坦克系统各部件的动力学模型（具体各部件动力学建模本文不深入阐述），结合RecurDyn/Control 模块实现坦克系统的动力学仿真，可获得不同行进速度和路面等级下的坦克身管振动特性数据。

4.2 射击时机仿真分析

已知某坦克击发时延约为10 ms，以30 km/h 的车速对2 000 m 外宽4.0 m×2.0 m 的固定目标实施行进间射击，高低向及方位向的火炮回转半径Rgd=5.5 m，Rfw=6.5 m；其对应的方位向的门限值约为Mθ=0.96 mil，高低向门限值约为Mφ=0.48 mil，其弹丸在飞行距离上的平均飞行速度v=1 600 m/s。

图6 和图7 是随机截取的坦克30 km/h 行进速度下的一段200 s 的身管振动数据，共20 000 个数据点（含高低及方位向身管的角度、角速度、角加速度）。

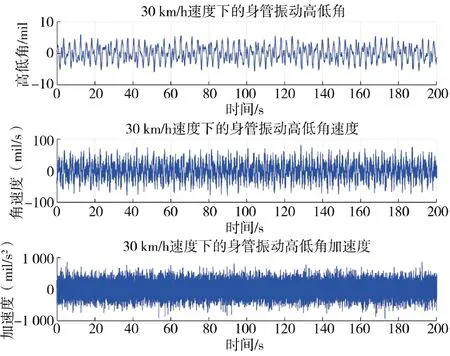
图6 身管高低角/角速度/角加速度曲线Fig.6 Curve of elevation/angular velocit/angular acceleration of tank gun barrel

图7 身管振动方位角/角速度/角加速度曲线Fig.7 Curve of azimuth/angular velocity/angular acceleration of tank gun barrel vibration

基于身管振动数据，对每一数据点分别采用简单射击门、延迟门、速度门以及预测射击门的判断逻辑来决定该数据点是否为有效射击点，形成如表1 的统计结果，表中ps为有效射击时机点数，bl（比率）部分以各类射击门判断的有效射击点数为分子，以简单射击门的有效射击点数为分母，计算的百分比。

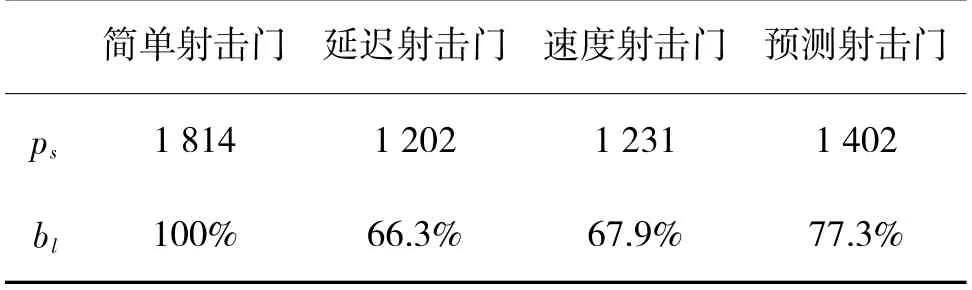
表1 不同射击门对应的射击时机统计Table 1 Firing opportunity statistical result based on different firing gates

以一次完全穿越过程的身管运动数据为例，其身管运动轨迹如图8 的圆点迹（身管由下至上运动），简单射击门限值如图8 中红色矩形框所示。图8（a）～图8（d）分别对应基于简单射击门、预测射击门、延迟射击门，以及速度射击门模型决定的有效射击时机（用“×”表示）。由图8 可知，相对延迟射击门、速度射击门对应的射击时机，预测射击门的射击时机更多，且预测射击门可把握身管尚处于简单射击门外的射击时机，如图8（b）所示。

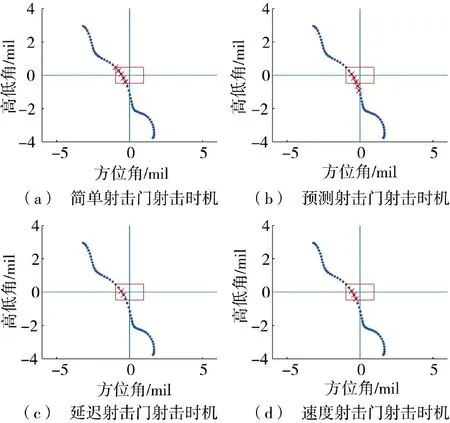
图8 不同射击门的射击时机Fig.8 Firing opportunity of different firing gate

由数值仿真的统计结果和单次身管穿越过程对射击时机的判断上看，本文给出的基于预测机制的射击门体制，能更充分地判断和利用有效的射击时机，同时能把原本不合理的射击时机剔除，有利于坦克火控更合理捕捉有效射击时机，提高坦克高速行进间的射击效能。

5 结论

本文针对射击门对高速行进间坦克有效射击时机的判断问题，分析了已有射击门在控制逻辑上的不足，并给出了基于预测机制的射击门数学模型。通过数理仿真分析，相较简单射击门、延迟射击门和速度射击门，本文给出的射击门模型简单可行，可获得更多的射击时机，也能避免无效击发，这对于提升高速行进间坦克的射击命中率具有现实意义。