创新试题·强化思维·凸显素养
2024-04-07王世朋钱良辰胡浩
王世朋 钱良辰 胡浩

摘 要:通过对2023年全国新高考Ⅰ卷的维度分析与命题特色透视,阐述新高考数学试题之印象,并对新课程标准、新教材、新高考背景下的复习教学提出建议.
关键词:新高考;数学试题;维度分析;特色透视;备考建议
中图分类号:G633.6 文献标识码:A 文章编号:1673-8284(2024)01-0050-07
引用格式:王世朋,钱良辰,胡浩. 创新试题·强化思维·凸显素养:2023年全国新高考Ⅰ卷试题
分析与备考建议[J]. 中国数学教育(高中版),2024(1):50-56.
基金项目:合肥市“十三五”规划课题——高中生数学活动经验内容与获得途径的实践研究(HJ19042).
作者简介:王世朋(1982— ),男,中学高级教师,主要从事数学课堂教学与信息技术辅助教学研究;
钱良辰(1991— ),男,中学一级教师,主要从事试题和信息技术辅助教学研究;
胡浩(1968— ),男,正高级教师,安徽省特级教师,主要从事中学数学课程、教材与教学研究.
研究和分析高考试题,把握考试动向,能为高三复习备考工作指明方向. 文章重点围绕2023年高考数学全国新高考Ⅰ卷试题,对其在试卷维度、命题特色方面呈现的特点进行分析,发挥高考的育人功能和导向推动作用,并结合后期的复习,给出一些备考建议.
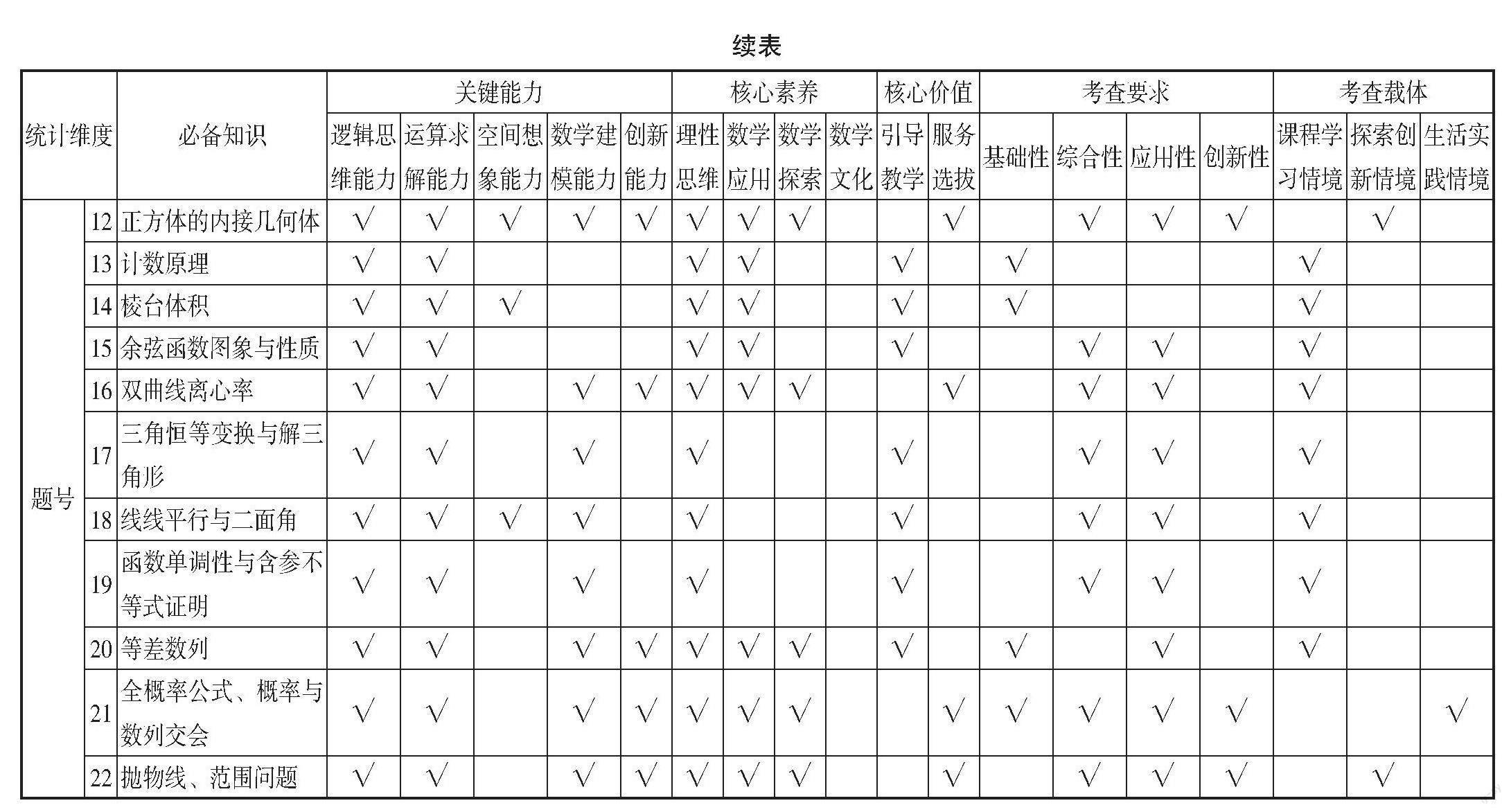
一、试卷维度分析
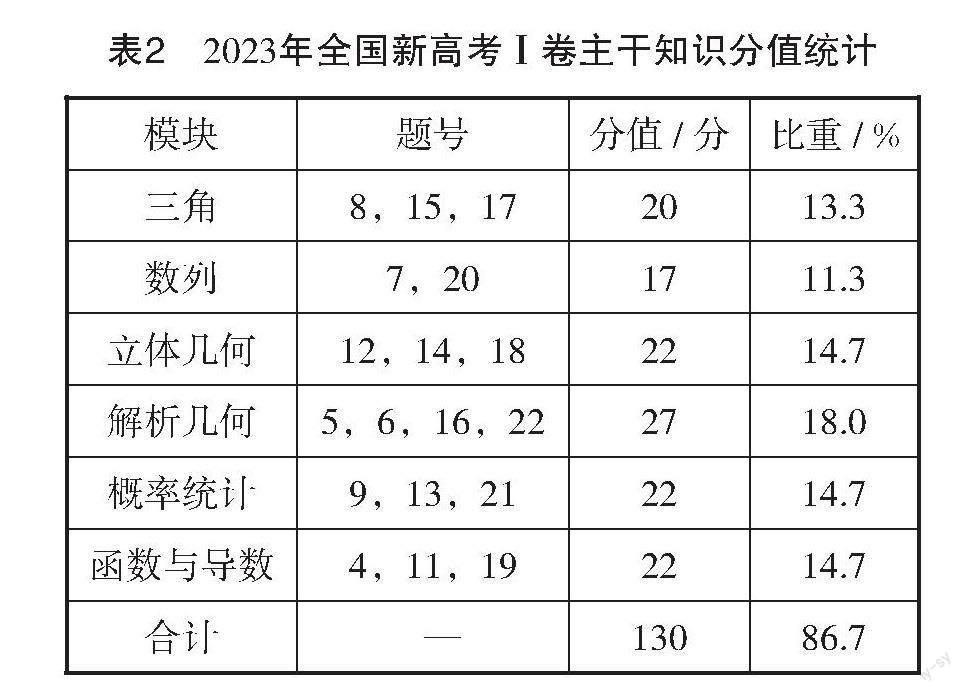
为了更细致和全面地进行分析,对2023年全国新高考Ⅰ卷的考查项目(重点是必备知识、关键能力、学科素养、核心价值、考查要求和考查载体)、考点分布及主干知识所占分值进行统计,如表1和表2所示.
基于上面的统计,不难看出:2023年全国新高考Ⅰ卷强化对主干知识的重点考查,要求学生深刻理解基本概念、性质和原理;突出对学生数学思维的测试,考查学生基于真实情境分析问题和解决问题的能力,凸显对数学核心素养的测评.
二、命题特色透视
1. 注重基础,考查主干知识
高考数学全国卷试题坚持以“一核、四层、四翼”为命题出发点,聚焦学科核心内容,坚持对主干知识和常规方法的考查,凸显对数学关键能力和数学核心素养的考查. 2023年全国新高考Ⅰ卷中的试题很好地贯彻了这一理念,突出主干知识,强化对基础知识的考查. 例如,第1题考查集合的交集运算,第2题考查复数的运算,第3题考查平面向量的坐标运算,第4题考查复合函数的单调性,第9题考查数据的数字特征,第13题考查计数问题,这些试题都是对学生基础知识掌握情况的测试. 再从主干知识来看,三角函数与解三角形涉及两道客观题、一道解答题,共20分;数列涉及一道客观题和一道解答题,共17分;立体几何涉及两道客观题和一道解答题,共22分;解析几何涉及三道客观题和一道解答题,共27分;概率统计涉及两道客观题和一道解答题,共22分;函数与导数涉及两道客观题和一道解答题,共22分. 整份试卷很好地体现了高考重点知识重点考查、促进教学回归课堂与教材、夯实学生成长的基础功能.
例1 (第3题)已知向量[a=1,1,b=1,-1],若[a+λb⊥a+μb],则( ).
(A)[λ+μ=1] (B)[λ+μ=-1]
(C)[λμ=1] (D)[λμ=-1]
解法1:因为[a=1,1,b=1,-1],
所以[a+λb=1+λ,1-λ],[a+μb=1+μ,1-μ].
由[a+λb⊥a+μb],得[a+λb ? a+μb=0],
即[1+λ1+μ+1-λ1-μ=0].
整理,得[λμ=-1].
故答案选D.
解法2:由[a+λb⊥a+μb],得[a+λb ? a+μb=0,]
即[a2+λ+μa ? b+λμb2=0].
因为[a=b=2,a ? b=0],
所以[λμ=-1].
故答案选D.
【评析】以向量的坐标计算为背景,考查向量的模及向量垂直问题. 解法1根据向量[a,b]的坐标,分别表示出向量[a+λb,] [a+μb]的坐标,把条件直译为方程进行求解,体现通性通法;解法2根据已知条件得到关于[a, b,a ? b]的关系式,再利用向量[a,b]的坐标进行求解,该方法计算量稍小.
2. 真实情境,考查关键能力
试题中充分体现了创新问题的设计. 例如,第10题以噪声污染问题为背景定义声压级,结合对数运算和不等式,旨在考查学生的逻辑推理能力、数学运算能力和数学建模能力. 又如,第12题以正方体的内接几何体为背景,重点对学生的空间想象能力、逻辑思维能力和创新能力进行考查,尤其是选项C和选项D,可以联想将签字笔或月饼等实物放入正方体盒子中的生活情境,有利于考查学生的直观想象能力. 再如,第21题以真实情境为背景考查概率统计和数列的相关知识,实现了对学生数学建模能力和运算求解能力的考查.
例2 (第12题)下列物体中,能够被整体放入棱长为1(单位:[m])的正方体容器(容器壁厚度忽略不計)内的有( ).
(A)直径为[0.99 m]的球体
(B)所有棱长均为[1.4 m]的四面体
(C)底面直径为[0.01 m],高为[1.8 m]的圆柱体
(D)底面直径为[1.2 m],高为[0.01 m]的圆柱体
解:对于选项A,因为[0.99 m<1 m],即球体的直径小于正方体的棱长,所以球体能够被整体放入正方体内,故选项A正确.
对于选项B,因为正方体的面对角线长为[2 m],且[2 m>1.4 m],所以该四面体能够被整体放入正方体内,故选项B正确.
对于选项C,因为正方体的体对角线长为[3 m],且[3 m<1.8 m],所以该圆柱体不能够被整体放入正方体内,故选项C错误.
对于选项D,因为[1.2 m>1 m],可知底面正方形不能包含圆柱的底面圆. 如图1,若底面直径为[1.2 m]的圆柱与正方体的上、下底面均相切,设圆柱的底面圆心为[O1],与正方体的下底面的切点为[M],可知[AC1⊥][O1M,O1M=0.6 m],则[tan∠CAC1=CC1AC=O1MAO1],即[12=][0.6AO1],解得[AO1=0.62 m]. 则圆柱的高为[3-2×0.62≈]
[0.035 2>0.01]. 所以该圆柱能够被整体放入正方体内.故选项D正确.
综上所述,答案选ABD.
【评析】以正方体的内接几何体为背景,考查学生的逻辑推理能力和空间想象能力. 选项A和选项B很容易确定. 对于选项C,柱体沿着正方体体对角线所在直线放置,容易确定选项C错误. 对于选项D,可以先看到圆柱体底面不能放在正方体底面正方形内,沿用选项C的想法,可以判断选项D正确. 对选项C和选项D的判断可以联想将签字笔或月饼等实物放入正方体盒子中的生活情境,对学生的直观想象能力进行了充分考查.
3. 突出理性,考查学科素养
理性思維在数学核心素养中起着最本质、最核心的作用. 试题突出地将关键能力与数学应用、数学探索、数学文化统一到理性思维的主线上,实现了对数学核心素养的重点考查. 对逻辑推理素养的考查在大多数试题中都有体现. 例如,第4题、第6题、第7题、第11题、第12题、第15题、第16题、第18题、第19题和第22题. 特别是第11题,以抽象函数为背景,重点考查学生的数学抽象、逻辑推理和数学运算素养,是学生综合素养的体现.
例3 (第11题)已知函数[fx]的定义域为R,[fxy=y2fx+x2fy],则( ).
(A)[f0=0]
(B)[f1=0]
(C)[fx]是偶函数
(D)[x=0]为[fx]的极小值点
解:由题意,知[fxy=y2fx+x2fy].
对于选项A,令[x=y=0],得[f0=0f0+0f0=0,]故选项A正确.
对于选项B,令[x=y=1],得[f1=1f1+1f1],则[f1=0],故选项B正确.
对于选项C,令[x=y=-1],[f1=f-1+f-1=][2f-1],则[f-1=0]. 令[y=-1],得[f-x=fx+x2 ·]
[f-1=fx]. 因为函数[fx]的定义域为R,所以函数[fx]为偶函数,故选项C正确.
对于选项D,当[x2y2≠0]时,对[fxy=y2fx+][x2fy]两边同时除以[x2y2],得到[fxyx2y2=fxx2+fyy2]. 故可以设[fxx2=lnx x≠0],则[fx=x2lnx,x≠ 0,0,x=0.]
当[x>0]时,[fx=x2lnx],则[fx=2xlnx+x2 ?][1x=x2lnx+1]. 令[fx<0],得[0
综上所述,答案选ABC.
【评析】利用赋值法能较容易确定选项A、选项B和选项C的正误. 对于选项D,要注意到条件可以处理为[fxyx2y2=fxx2+fyy2,xy≠0],其形式为[gxy=][gx+][gy],该函数的基本原型为对数函数. 由此可以构造函数[fx=x2lnx,x≠ 0,0,x=0.] 而该题并没有要求函数为非常函数,故直接令[fx=0]即可确定结果. 该题以学生熟悉的抽象函数为出发点命制,知识起点低,但对学生思维能力的要求逐渐提高.
4. 破除套路,强化灵活应用
2023年全国新高考Ⅰ卷中部分试题对主干知识的考查改变了以往的命题形式或调整了考查顺序,旨在引导师生改变原有认识,真正体现对学生“四基”的考查,突出“四能”. 例如,第8题的三角恒等变换、第19题的导数、第20题的数列均改变了考查顺序. 另外,第20题对数列的考查以求和或与不等式结合的命题形式,围绕等差数列的定义和性质,注重对式子的分析与处理,在考查学生逻辑推理和数学运算素养的同时,考查学生的临场应变能力. 解答题第22题同样打破了解析几何试题求解的基本套路,需要通过放缩把双变量问题转化为单变量问题,再构造函数求解,充分考查了学生对不同知识的灵活运用能力.
例4 (第20题)设等差数列[an]的公差为[d],且[d>1].令[bn=n2+nan],记[Sn,Tn]分别为数列[an, bn]的前[n]项和.
(1)若[3a2=3a1+a3,S3+T3=21],求[an]的通项公式;
(2)若[bn]为等差数列,且[S99-T99=99],求[d].
解:(1)因为[an]为等差数列, [3a2=3a1+a3],
所以[3d=a1+2d],解得[a1=d].
所以[S3=3a2=3a1+d=6d].
因为[T3=b1+b2+b3=2d+62d+123d=9d],
所以[S3+T3=6d+9d=21],即[2d2-7d+3=0].
解得[d=3]或[d=12](舍去).
所以[an=a1+n-1d=3n].
(2)因为[bn]为等差数列,
所以[2b2=b1+b3],即[12a2=2a1+12a3].
所以[61a2-1a3=6da2a3=1a1],
即[a21-3a1d+2d2=0].
解得[a1=d]或[a1=2d].
由[d>1],得[an>0].
因为[S99-T99=99],
所以由等差数列性质知[99a50-99b50=99],
即[a50-b50=1].
所以[a50-2 550a50=1],即[a250-a50-2 550=0].
解得[a50=51]或[a50=-50](舍去).
当[a1=2d]时,[a50=a1+49d=51d=51],
解得[d=1],与[d>1]矛盾,无解;
当[a1=d]时,[a50=a1+49d=50d=51],
解得[d=5150].
综上所述,[d=5150].
【评析】第(1)小题,根据等差数列的通项公式建立方程求解即可. 第(2)小题,由[bn]为等差数列,得[a1=d]或[a1=2d]. 再由等差数列的性质,得[a50-b50=1]. 分类讨论即可得解. 关键是对条件“[bn]为等差数列”进行转化,最优选择是考虑前三项,再讨论检验.
5. 服务选才,指向教考衔接
高考的核心功能是立德树人、服务选才、引导教学. 加强教考衔接是高考命题改革的既定方针. 例如,第21题和第22题特别强调对学生逻辑思维能力和创新能力的考查,与《教育部关于做好2023年普通高校招生工作的通知》中提到的“服务人才培养质量提升和现代化建设人才选拔”的选拔要求高度契合. 试题坚持素养导向、能力为重,对发挥科学选拔与育人导向功能有着积极的示范和引领作用,以考促学,为后期数学教学明确了努力的方向.
例5 (第22题)在直角坐标系[xOy]中,点[P]到[x]轴的距离等于点[P]到点[0, 12]的距离,记动点[P]的轨迹为[W].
(1)求[W]的方程;
(2)已知矩形[ABCD]有三个顶点在[W]上,证明:矩形[ABCD]的周长大于[33].
解:(1)设[Px,y],则[y=x2+y-122].
两边平方并化简,得[y=x2+14].
故[W]的方程为[y=x2+14].
(2)(方法1)设矩形的三个顶点[Aa,a2+14,][Bb,b2+14,Cc,c2+14]在[W]上,且[a 则[kABkBC=-1,a+b 令[kAB=b2+14-a2+14b-a=a+b=m<0]. 同理,令[kBC=b+c=n>0],且[mn=-1], 则[m=-1n]. 设矩形周长为[C],由对称性知[m≥n]. 不妨设[0 则[12C=AB+BC=b-a1+m2+c-b1+n2≥][c-a1+n2=n+1n1+n2]. 由[n>0],易知[n+1n1+n2>0]. 令[fx=x+1x21+x2,x∈0,1], 得[fx=2x+1x22x-1x]. 令[fx=0],解得[x=22]. 當[x∈0, 22]时,[fx<0],此时[fx]单调递减; 当[x∈22,1]时,[fx>0],此时[fx]单调递增. 则[fxmin=f22=274]. 故[12C≥274=332],即[C≥33]. 由上可知,两个等号成立的条件分别为[n=1],[n=22],显然不成立. 故[C>33],得证. (方法2)不妨设点[A,B,D]在[W]上,且[BA⊥DA]. 依题意,设[Aa,a2+14]. 易知直线[BA],[DA]的斜率均存在且不为0, 则设[BA],[DA]的斜率分别为[k]和[-1k]. 由对称性,不妨设[k≤1]. 直线[AB]的方程为[y=kx-a+a2+14], 联立方程,得[y=x2+14,y=kx-a+a2+14.] 整理,得[x2-kx+ka-a2=0]. 因为判别式[Δ=k2-4ka-a2=k-2a2>0], 所以[k≠2a]. 所以[AB=1+k2k-2a]. 同理,可得[AD=1+1k21k+2a]. 故[AB+AD=1+k2k-2a+1+1k21k+2a] [≥1+k2k-2a+1k+2a] [≥1+k2k+1k] [=1+k2k+1k]. 令[x=k>0],得[fx=x+1x21+x2,x>0]. 下同方法1. 【评析】该题考查了抛物线和不等式的综合应用. 第(1)小题直译条件,列出方程化简即可,然而结果并非抛物线的标准方程. 第(2)小题求解的前半部分是对圆锥曲线的一般处理方式,方法1设点和方法2设直线的目的均是要把矩形的半周长表达出来. 再通过放缩,把双变量问题转化为单变量问题. 最后构造函数,利用导数研究单调性和最值. 求解该小题最大的难点不在于对圆锥曲线的处理,而在于对放缩法的运用. 该题整体难度较大,鲜明地体现出高考的选拔性. 三、复习备考建议 1. 回归教材,挖掘教材资源 教材永远是最好的备考素材. 在当前的复习备考中,回归教材很多时候仅停留在口头上,行动上基本没有实际举措. 即使有回顾,大多数也是基于复习资料一带而过. 学生长期困于复习资料和海量的题目中,甚至在高考复习期间也从未翻看过教材. 这些都是极其可怕的现象. 2023年全国新高考Ⅰ卷中有很多试题可以在教材中找到相关素材. 例如,第7题考查等差数列的性质,与人教A版《普通高中教科书·数学》(以下统称“人教A版教材”)选择性必修第二册第25页习题的第7题几乎一致;第8题考查三角恒等变换,与人教A版教材必修第一册第229页习题第9题的题干条件相似,均是两角差正弦公式的直接展开,结合方程思想来处理;第21题的第(2)小题考查了概率和数列的交会问题(马尔科夫模型),而在人教A版教材选择性必修第二册第39页的例12中有过类似的研究,这是典型的对学生知识迁移能力的考查. 总之,高考复习备考中,师生不能忽视教材,更不能抛弃教材,需要认真研究教材中基于情境设置的例题和课后习题,当然也要特别重视对教材中“阅读与思考”“探究与发现”材料的运用,甚至可以组织备课组教师对教材上的相应资源进行有效整合、合理改编,生成课堂复习素材和课后训练主材,以提升复习备考效率. 2. 有效引导,培养数学思维 在高考复习备考过程中,师生要把思想与方法训练放在首位,把核心素养的落实谨记于心. 对于高考试题,师生要加强研究,明确问题导向,避免盲目刷题、机械应试,以增强复习备考的效率. 死记公式和机械训练只能实现简单模仿,不能做到举一反三. 缺乏理解和运用能力的非创新性人才培养并不是教育的最终目的. 要想真正提高学生解决问题的水平,教与学必须做出积极调整,即加强对学生数学思维的训练. 要想拥有创新性思维方式,学生不仅要真正掌握基础知识,还要有灵活运用知识解决问题的能力. 事实上,学生通过自身较难进行行为调整,此时教师的引导作用就显得意义重大. 对于复习教学工作,首先,教师要能转变教学理念,认识到思维的培养需要学生的亲身体验,需要教师强化教学活动的设计和引领. 其次,在课堂中,教师要积极调整传统的教学行为,从原有的填鸭式教育,满堂灌、一言堂的授课方式,转变为合作式、探究式和体验式的课堂教学. 最后,还需要教师充分调动学生的主观能动性,把课堂还给学生,让真实、有效的生生對话、师生对话时常发生在课堂中,让学习在课堂中真正发生,切实提升学生思维的深度和广度. 虽然学生的数学思维存在差异,但是教师的有效引导对改善和提升学生的数学思维品质必然可以发挥积极的作用,需要教师长期坚持. 3. 强化发展,提升创新能力 2023年全国新高考Ⅰ卷特别融入创新试题的考查,对学生分析问题、解决问题的能力要求很高. 例如,第20题区别于以往的数列试题,是仅基于等差数列基本概念命制的创新题. 所谓创新试题,虽然在试题呈现方式或设问角度方面比较新颖,但是其考查的基础知识、基本技能和基本思想不变,即“万变不离其宗”,只要抓住问题的本质,面对创新试题也能做到游刃有余. 在教学过程中,教师不仅要强化对学生“四基”的培养,还要提升学生的迁移类比能力. 同时,教师要不断强化对学生的学法指导,从学生学情出发,增强指导的具体性、可操作性和有效性,帮助学生调适好心态,以积极的态度、务实的举措、科学的方法学好每节课,完成每次训练. 参考文献: [1]教育部考试中心. 中国高考评价体系[M]. 北京:人民教育出版社,2019. [2]教育部考试中心. 创设情境发挥育人作用 深化基础考查核心素养:2022年高考数学全国卷试题评析[J]. 中国考试,2022(7):14-19.
