让练习课丰润、深厚起来——以苏教版数学五年级上册“多边形的面积”单元整理与练习为例

江苏省丹阳市华南实验小学 蒋明玉 钱定娟

笔者曾上过一节“多边形的面积”单元整理与练习课。对于这样的整理与练习课到底该怎么上，笔者边实践边思考，整理如下，以期给大家提供一些参考。

一、反刍推导过程，形成知识网络图

片段一：

师：除了画图，有的同学列表整理，有的同学用文字描述。虽然你们整理的方式不一样，但内容都差不多。大家都整理了三个图形的面积公式，有的同学还整理了推导过程。那么，这三个公式是怎么推导来的呢？和你的同桌说一说。

师：如果我们不除以2，那求的是什么？

师：掌握面积公式的推导过程有助于我们对面积公式的理解。推导这几种图形的面积公式时，有什么相同的地方？（生：转化）是的，转化是一种重要的数学思想方法，也是一条有效的解决问题的策略。知识获得的背后，渗透着有力量的思想方法！学习新知时，大家可以把新知转化成旧知，利用旧知推导出新知，新旧知识之间有着密切的联系。

师板书：

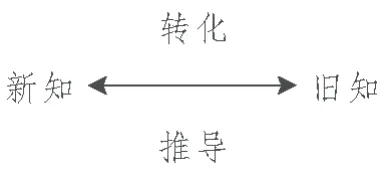
师：这几个图形的面积公式之间有着怎样的联系？你能把图形摆一摆，画箭头表示它们之间的联系吗？（出示合作要求，小组合作后反馈交流）

师：如果把“多边形的面积”这部分知识看作一棵知识树的话，树根、枝干分别是怎样的？

师（总结）：长方形的面积公式就是这棵大树的树根，是基础。平行四边形、三角形、梯形的面积公式是枝干，只有根扎实了，才能枝繁叶茂，我们的每项学习都是如此。

执教反思：

学生课前进行了单元自主整理，但是，他们基本上是围绕“公式”以及公式的“推导过程”展开的。知识的获得渗透了强有力的思想方法，在整理“多边形的面积”单元内容时，笔者除了让学生自己整理三个新学的面积公式，回顾其推导过程，还让学生体会到将新知“转化”成旧知，利用旧知“推导”新知。长方形、平行四边形、三角形、梯形的面积公式推导过程中，每一个知识的产生都是由“新”入“旧”，既是这一次的“转化”，也是下一次的“推导”。学生在这样的学习过程中领悟新旧知识间的联系，再把图形按一定的顺序摆一摆，有的学生甚至想到了“联系图”。

随后，教师话锋一转：“如果把它旋转一下，会怎么样？”知识网络结构图跃然于黑板上时，学生豁然体会到整理的“魅力”。教学时，教师要适时介入、勇敢退出，在推导公式的回顾环节，让学生同桌互说后上台展示，最终完成任务。而提炼思想方法、产生知识网络图等任务，需要教师逐步引导学生完成。

课前独立整理，课中沟通知识间的联系，如此，课堂便精彩纷呈！在知识整理的背后，揭示主要的思想方法，教师只是适时、适度地“介入”，巧妙地点拨、高效地追问，把数学课堂构建成学生数学思考的“渔场”。学生的观察、概括、分析等能力在这个“渔场”中得以孕育、成长，思维在这个“渔场”上纵情驰骋。

二、用足练习资源，知识变丰润、深厚

片段二：

师：图1 中的画图任务有几个要求？（一标数据，二写算式）

图1

（生交流）

师：平行四边形画底为5、高为3，除了这样画还可以有别的方法吗？（课件相应展示）除了画底为5、高为3，还可以怎样画？

生1：底为3，高为5。

生2：底为15、高为1，还有底为1、高为15，但是这两种方法因为画出来太“占地”，所以一般我们都不这样画。

师：那三角形呢？如果画的底是5，高应画多少？怎么想的？也能画出不同形状来吗？

师：梯形呢？高还是画6，上下底的和得画多少呢？

师：（如图2）看，我们一共画了四组图形，看每一组的图形，你想到了什么？

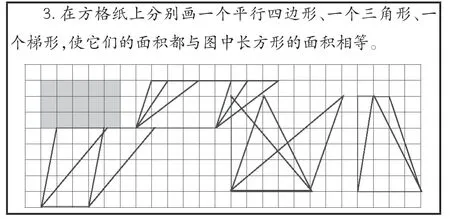
图2

生：等底等高，面积相等。

师：只看平行四边形和三角形这两组（如图3），怎么样？你发现了什么？

图3

生：面积相等、底相等，高是2 倍或一半的关系。

师：只看三角形和梯形这两组（如图4），你又发现了什么？

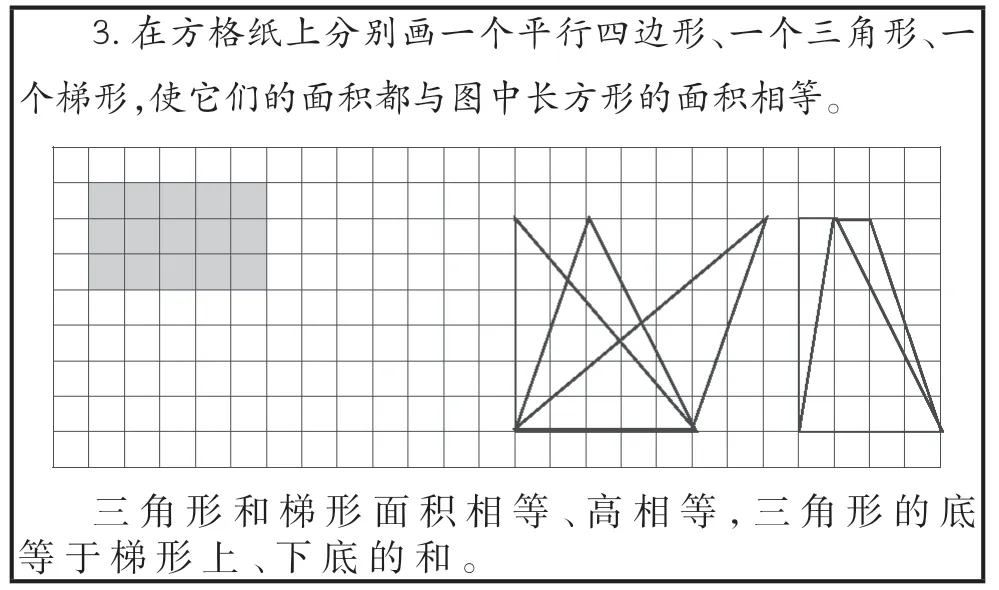
图4

师：从右往左看，当梯形的上底为0 时，就成了什么图形？（生：三角形）当梯形的上、下底相等时，就成了什么图形？（生：平行四边形）。数学知识间的联系实在太紧密了！

执教反思：

这一道练习题的处理，分成了三个层次。第一层次：学生根据要求自主完成。第二层次：除了这样画，还可以怎么画？第三层次：比较这两组图，你发现了什么？先让学生画一画，通过“标数据”“写算式”等手段，“画”的正确率可想而知。但教师对练习资源的利用不止步于此，出示了底和高分别等于长方形的长和宽的平行四边形，并在追问中出示另一组不与其等底等高的平行四边形，再在追问中出示一组三角形、一组梯形……然后，课件通过隐去其余的图形，聚焦于要比较的两组图形，让学生比较：两种图形中面积、底、高三个量中，若有两个量是相等的，第三个量又会有怎样的联系。学生轻松得出结论：平行四边形和三角形面积相等、底相等，三角形的高是平行四边形的2 倍；三角形和梯形面积相等、高相等，三角形的底等于梯形上、下底的和……

这样的安排，旨在让学生用自己的“眼光”“思维”“语言”，去“观察”，去“思考”，去“表达”，发现图形之间的联系，发现面积、底、高三者之间千丝万缕的联系。知识的整理如果只是复习的一种形式，那就失去了价值。只有引导学生抓住知识的内在联系，从不同角度、不同层次展开触动思维的整理，学生才能从简单的“概念知道”迈向深刻的“智性思考”。

三、题组对比练习，“变”中寻找“不变”

片段三：

结束了上一个画图练习后，教师出示如图5 的题组对比练习，让学生在“变”中寻找“不变”，周长、面积在三种情况下到底“变”还是“不变”。第一种情况是推导平行四边形面积公式时的转化，第二种情况是这节新授课后的巩固练习题，第三种情况是教材上单元整理与练习“探索与实践”中的习题。第一种情况，在新课的学习中，学生更多聚焦于面积的不变，而对周长怎样、有没有变化没有做过多研究；第三种情况，学生容易将其与第二种情况混淆，难以看出高的不变，确定高不变、面积不变时，对于周长有没有变化又变得犹豫不决了。

图5

执教反思：

所谓“题组”，就是将内容联系密切、题目形式相似、思维方法相近、解答方式相同或有联系的题目串联在一起构成一组题。它具有鲜明的对比性、层次性、迁移性和实效性，对学生巩固所学知识、纠正思维偏差、增强解题能力、形成知识网络、发展思维能力等发挥着独特的作用。

教师通过题组教学盘活了教学内容，促进了学生主动构建知识结构，不仅对单个知识点有更加深刻的理解，还能将各个孤立的知识点串联成知识块，进而构建完整的知识结构。“为什么变了？”“为什么没有变？”“变大还是变小了？”“变长还是变短了？”……教师适时追问，与学生进行多向、深入的交流互动，激活了学生的知识，扩充了其思维的容量，将不同层次学生的思维推向更高处。题组教学演绎的丰富和多姿，成就了课堂教学的深刻和灵动！

四、设置“易错提醒”，纠错防错

片段四：

师：一个单元的学习结束了，老师整理了大家的“当堂检测”作业纸，收集了几道易错题，我们一起来看一看。

师（出示）：（1）三角形的面积是12 平方厘米，高是4 厘米，底是多少？（2）梯形的面积是24 平方厘米，上底是4 厘米，下底是8 厘米，高是多少？

师：第一题有一名同学是这样解答的（如图6），第二题有一名同学是这样解答的（如图7）。

图6

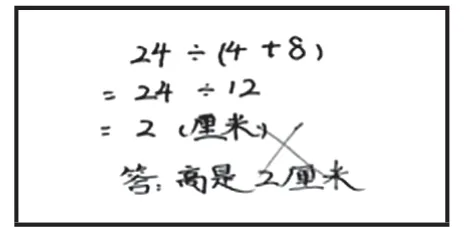
图7

师：找一找错误的原因是什么；说一说该怎样正确解答；想一想要提醒大家注意些什么。四人一组开始讨论，然后全班交流。

执教反思：

从2021 年春季开始，笔者所在学校在数学课堂中不再使用“作业本”，全面使用“当堂检测”作业纸，分“随堂练习”“当堂检测”两个板块，前一个板块主要配合课堂新授过程完成，可以是书上的“试一试”“练一练”或者“巩固练习”等，后一个板块则是精选的一些综合的分层练习。“多边形的面积”这一单元本身知识点繁多，且易错点多。在平时的练习中，教师要注意收集、积累学生的“典型错例”，单元整理练习时让学生“找一找错误的原因是什么”“说一说该怎样正确解答”“想一想要提醒大家注意些什么”，再现他们的错误，也唤醒他们的记忆，在“找一找”“说一说”“想一想”的过程中，加深学生对知识点的理解。

课堂生活本身就是丰富多彩的，“偏差”“失误”也必然是其中的一部分，当教师追求课堂的真实自然，敢于暴露学生的“错误”时，他们便会把教学时间放在促使学生积极思维上，使学生由被动的“执行者”转化为主动的“探究者”。这与课堂上直接出示同类题目练习相比，节省了练习时间，更发挥了前期练习的价值，充分利用“错误”资源，达到事半功倍的效果。