耦合环辅助多模光纤受激布里渊散射阈值分析
2024-04-03关莉珍王雨行刘嘉伟聂鹏程闫煜鹏宋锡策余先伦
关莉珍,王雨行,刘嘉伟,聂鹏程,闫煜鹏,宋锡策,余先伦
(重庆三峡学院 电子与信息工程学院,重庆 404020,中国)
0 引 言
面对网络传输时代更高速的规划需求及人们日益增长的带宽需求,多模光纤因其得天独厚的容量优势,可以解决单模光纤传输达到容量极限的问题,将在未来光纤通信系统中发挥重要作用[1-3]。但是多模光纤(multi-mode fiber,MMF)众多模式在传输过程中,由于受到外界各种环境、人为等因素干扰,会发生模式耦合现象,致使模式间发生串扰,影响通信质量。近年来,有很多通过对光纤结构进行设计以减少模式耦合提升光纤传输性能的相关研究,如空心光纤、弱耦合少模多芯光纤、偏振光纤和沟槽辅助光纤等新类型[4-12]。增大模式间有效折射率差值可以有效抑制串扰。
在整个光纤通信系统中,当入射光功率超过一定值时,会发生受激布里渊散射(stimulated Brillouin scattering,SBS)现象[13-14]。此现象是影响光纤传输系统中传输距离和容量的重要因素,会限制系统入纤功率的提升。参考文献[15]中研究了多模光纤中SBS阈值的理论和数值研究,但没有详细分析每种模式的阈值。参考文献[16]中提出并测试了一种通过管理光纤声学轮廓来抑制SBS的新方法,发现具有3层不同掺杂纤芯的光纤结构对受激布里渊散射阈值可以有效提升。参考文献[17]中对阶跃折射率少模光纤的受激布里渊散射阈值进行了理论分析。参考文献[18]中通过频率和相位调制提高受激布里渊散射阈值是抑制光纤通信中SBS的有效方法,适用于在入射光功率有限的情况。参考文献[19]中在多模光纤中采用选择性模式激励抑制受激布里渊散射,发现通过优化多模激励,可以进一步提高SBS阈值。
基于此,本文作者优化设计了一种耦合环辅助多模光纤结构,建立了耦合环辅助多模光纤结构中SBS阈值的数学模型,理论分析并数值计算耦合环辅助多模光纤光纤有效模场面积、不同阶数模式、衰减系数和纤芯半径对SBS阈值的影响,可以减少模式耦合,抑制模间串扰,且保持一定的模场面积。
1 耦合环辅助多模光纤结构

模式耦合是影响多模光纤通信质量的重要因素之一,在多模光纤中加入耦合环辅助结构可以有效减少模式耦合现象,提升通信质量。本文中设计的耦合环辅助多模光纤结构的横截面示意图如图1a所示。该结构相比于普通的阶跃折射率多模光纤结构多了两部分:纤芯中心和对称分布的耦合环,不同颜色代表不同折射率材料,其折射率分布图如图1b所示。图1b中,r0为中心低折射率耦合环半径,r1为中心耦合环外纤芯的外环半径,r2为高阶折射率耦合环的外环半径,rco为耦合环多模光纤的半径,nco为纤芯折射率,nw-为低折射率耦合环的折射率,nw+为高阶折射率耦合环的折射率,w-和w+分布为低折射率耦合环和高折射率耦合环的宽度,w为两耦合环中间纤芯宽度。
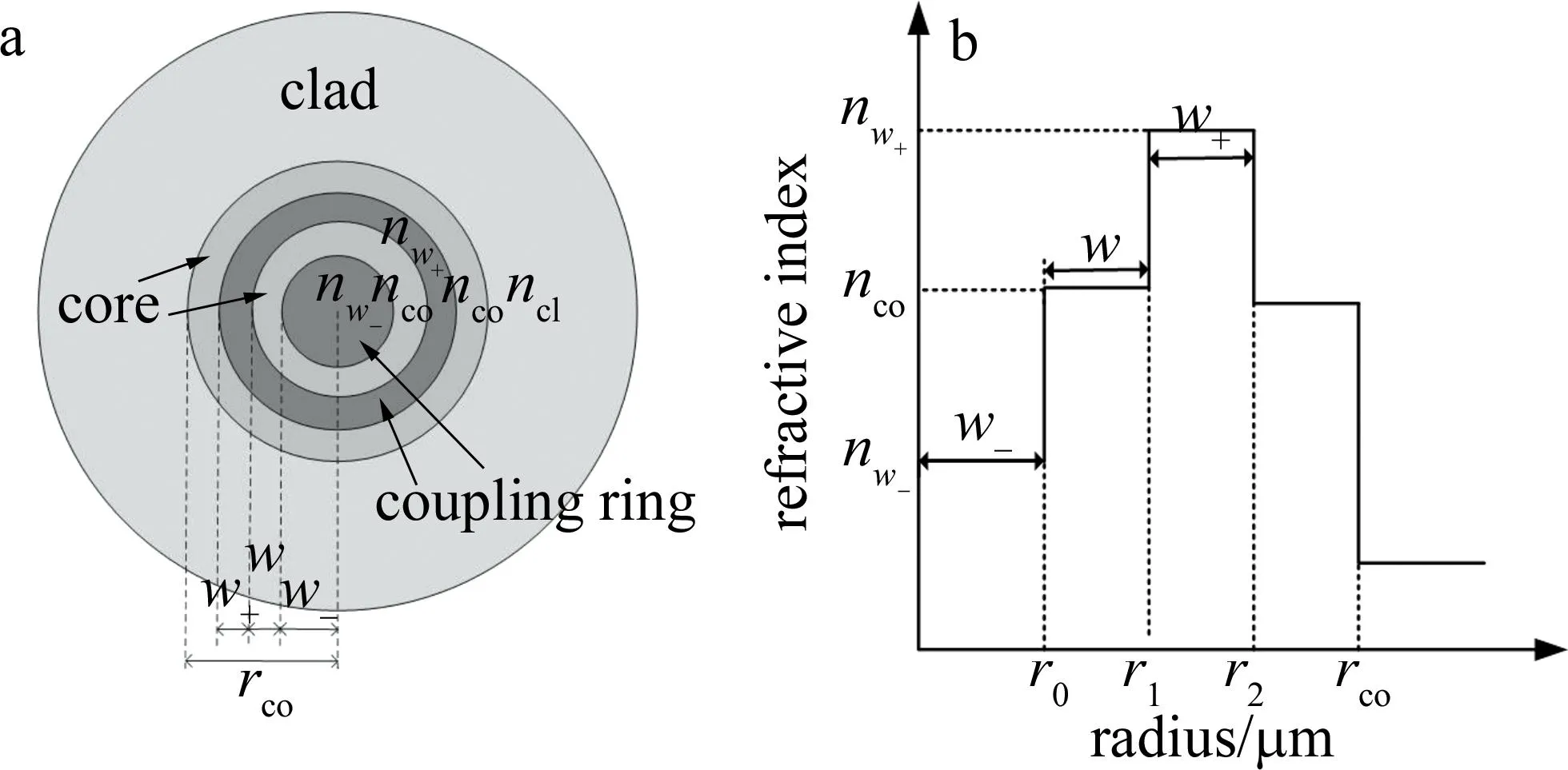
图1 耦合环辅助多模光纤结构特征图a—横截面示意图 b—折射率分布图Fig.1 Structure characteristics of coupling ring-assisted multi-mode fibera—cross-sectional diagram b—refractive index distribution
通过仿真软件对多模光纤建模,发现LP02和LP21两个模式有效折射率最接近,是影响模间串扰的关键。采用有限元法计算耦合环辅助多模光纤与常规阶跃多模光纤LP02与LP21模式的有效折射率,变化如图2所示。把其在1550 nm处的差值0.7×10-3与同环境下测得常规阶跃光纤的差值0.4×10-3进行对比,发现两模式间有效折射率差值提升了1.75倍,验证了耦合环辅助多模光纤结构串扰抑制的有效性。
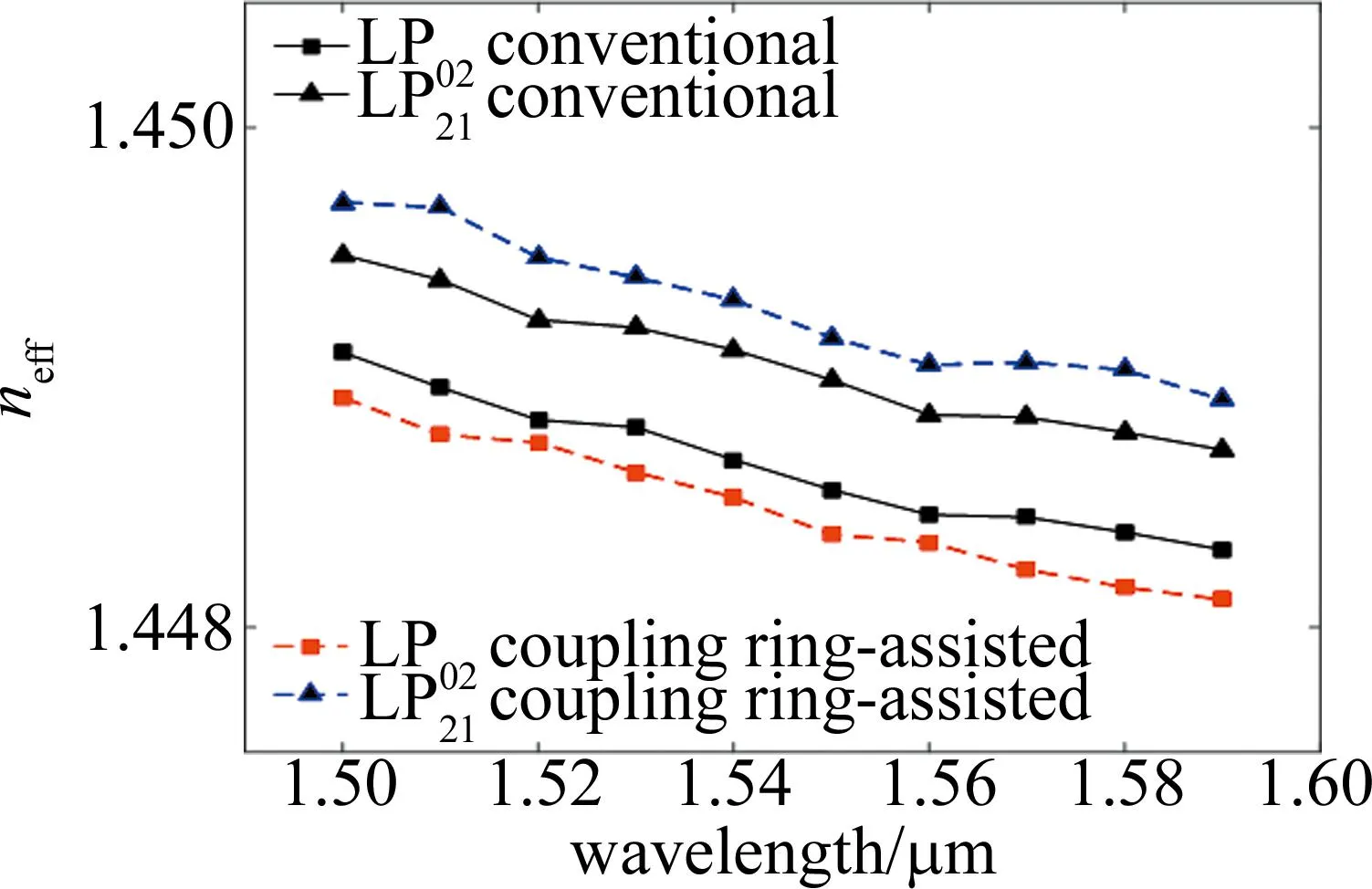
图2 耦合环辅助多模光纤与常规阶跃多模光纤LP02模和LP21模有效折射率分布图Fig.2 Effective refractive index distribution of coupling ring-assisted multi-mode fiber and conventional step multimode fiber LP02 and LP21 modes
2 耦合环辅助多模光纤SBS阈值理论模型
本文中通过常规多模光纤的SBS阈值模型,推导图1结构中SBS阈值理论模型。耦合环辅助多模光纤的布里渊增益谱服从洛伦兹分布,可以由布里渊频移、线宽和峰值增益系数等参量来描述。
布里渊频移不仅与散射光角度有关,且其值取决于光纤中传播光模式的有效折射率和相互作用的声模式的速度,耦合环的宽度及其折射率的改变都将引起传播光模式的有效折射率变化。在图1中,耦合环辅助多模光纤中的布里渊频移[14]可以表示为:
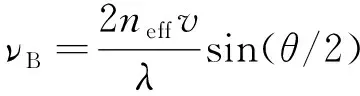
(1)
式中:neff是光纤中传输模式的有效折射率;v为光纤中的声速;θ为散射角。νB与散射角的关系为:布里渊频移在θ=π时得到最大值,定义为νB,max;在θ=0时得到最小值,定义为νB,min。
图1中耦合环辅助多模光纤中所传输模式的布里渊散射谱线宽[20]为:
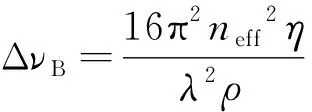
(2)
式中:ΔνB是布里渊散射谱的3 dB带宽,其值与光纤传播模式的有效折射率有关;ρ是光纤材料密度;η是运动粘滞系数。
耦合环辅助多模光纤可以有效减少多模光纤中的模式耦合现象,其布里渊散射增益谱[20]为:
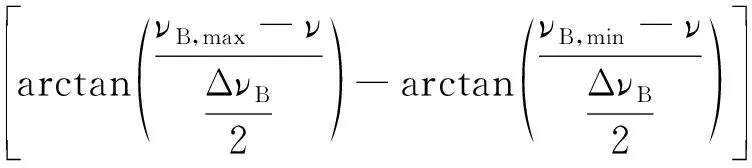
(3)
式中:g0为纯石英布里渊峰值增益。当入射光与Stokes光的频率差ν=νB时,布里渊散射谱的增益系数达到峰值,从式(3)得出其表达式[21]为:

(4)
式中:p12是光纤弹光系数;c是真空中光速。
阈值增益系数不仅与耦合环辅助多模光纤的有效长度有关,还与光纤的有效截面积和耦合环辅助多模光纤纤芯半径等很多因素有关,其表达式[17]为:
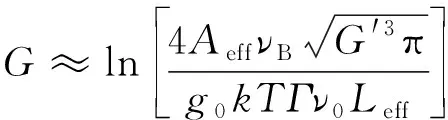
(5)
式中:布里渊阈值增益系数G的临界值G′≈21;k为玻尔兹曼常量;T为绝对温度;Γ为声子衰减速率;ν0为抽运波频率。光纤的有效长度Leff随着光纤长度L的变化与信号衰减系数α的关系表达式[17]为:

(6)
图1中由于耦合环的加入,其纤芯的有效模横截面积Aeff有所变化,表达式为:
Aeff=S2π[rco2-r02-(r22-r12)]
(7)
式中:S为图1中光纤模场面积与纤芯面积之比。多模光纤中SBS阈值的通用表达式[17]为:Pth=GAeff/(gBLeff)。将式(7)代入,可得图1耦合环辅助多模光纤的SBS阈值表达式为:

(8)
式中:r0为中心低折射率耦合环半径;r1为中心耦合环外纤芯的外环半径;r2为高阶折射率耦合环的外环半径;rco为耦合环辅助多模光纤的纤芯半径。
3 耦合环辅助多模光纤SBS阈值数值研究
根据图1耦合环辅助多模光纤结构及其SBS阈值理论模型,数值计算研究光纤有效模场面积、不同阶数模式、衰减系数和纤芯半径对耦合环辅助多模光纤SBS阈值的影响。本文中选定入射光波长为1550 nm,光纤衰减常数α=0.22 dB/km,纤芯折射率nco=1.46,包层折射率ncl=1.4462,纤芯直径d=50 μm,包层直径D=125 μm。
3.1 不同有效模场面积时,耦合环辅助多模光纤SBS阈值与光纤长度的关系
在多模光纤中加入耦合环辅助结构可以有效抑制模式耦合现象,减少模间串扰,但同时会影响纤芯的有效模场模面积。改变纤芯直径d,根据式(4)~式(8)数值计算,得到不同的有效模场面积下所测量的耦合环辅助多模光纤的SBS阈值,其值随光纤长度变化的情况如图3所示。

图3 SBS阈值随光纤长度的变化曲线Fig.3 Variation curve of SBS threshold with fiber length
从图3可以看出,耦合环辅助多模光纤纤芯有效模场面积虽不同,但其SBS阈值随光纤长度的变化趋势相同,在18 km距离范围内从急剧下降变至缓慢,在18 km后趋于一个定值。同时可以看出,有效模场面积越大,其SBS阈值就越大,当纤芯直径在50 μm~70 μm之间时,其SBS阈值为30 dBm~60 dBm。
3.2 耦合环辅助多模光纤各模式SBS阈值与光纤长度的关系
在图1耦合环辅助多模光纤中,选取LP01、LP11、LP21、LP02、LP31和LP036种模式,通过有限元方法得到各模式有效折射率分别为:1.4506,1.4498,1.4491,1.4484,1.4475和1.4463,运用式(1)~式(4)、式(8)对其阈值进行数值计算,分析它们在不同光纤长度上阈值的变化,结果如图4所示。

图4 各模式SBS阈值与光纤长度的关系Fig.4 Relationship between SBS threshold value of each mode and fiber length
从图4可以看出,耦合环辅助多模光纤的SBS阈值会随着模式阶数的增大而增大。且在10 km的光纤长度内,SBS阈值随着光纤长度的增加而减小,最终趋于30 dBm。
3.3 耦合环辅助多模光纤SBS阈值与衰减系数的关系
从式(6)可以看出,衰减系数与有效长度成反比,阈值又与有效长度成反比,故可知耦合环辅助多模光纤的SBS阈值与衰减系数成正比,其阈值会随着衰减系数的增大而增大。在一段长为20 km的光纤中,取阈值增益系数G=21,对衰减系数与SBS阈值的关系进行数值计算,结果如图5a所示。可以看出,耦合环辅助多模光纤的SBS阈值随着光纤衰减系数的增大而增大,两者呈正比关系。
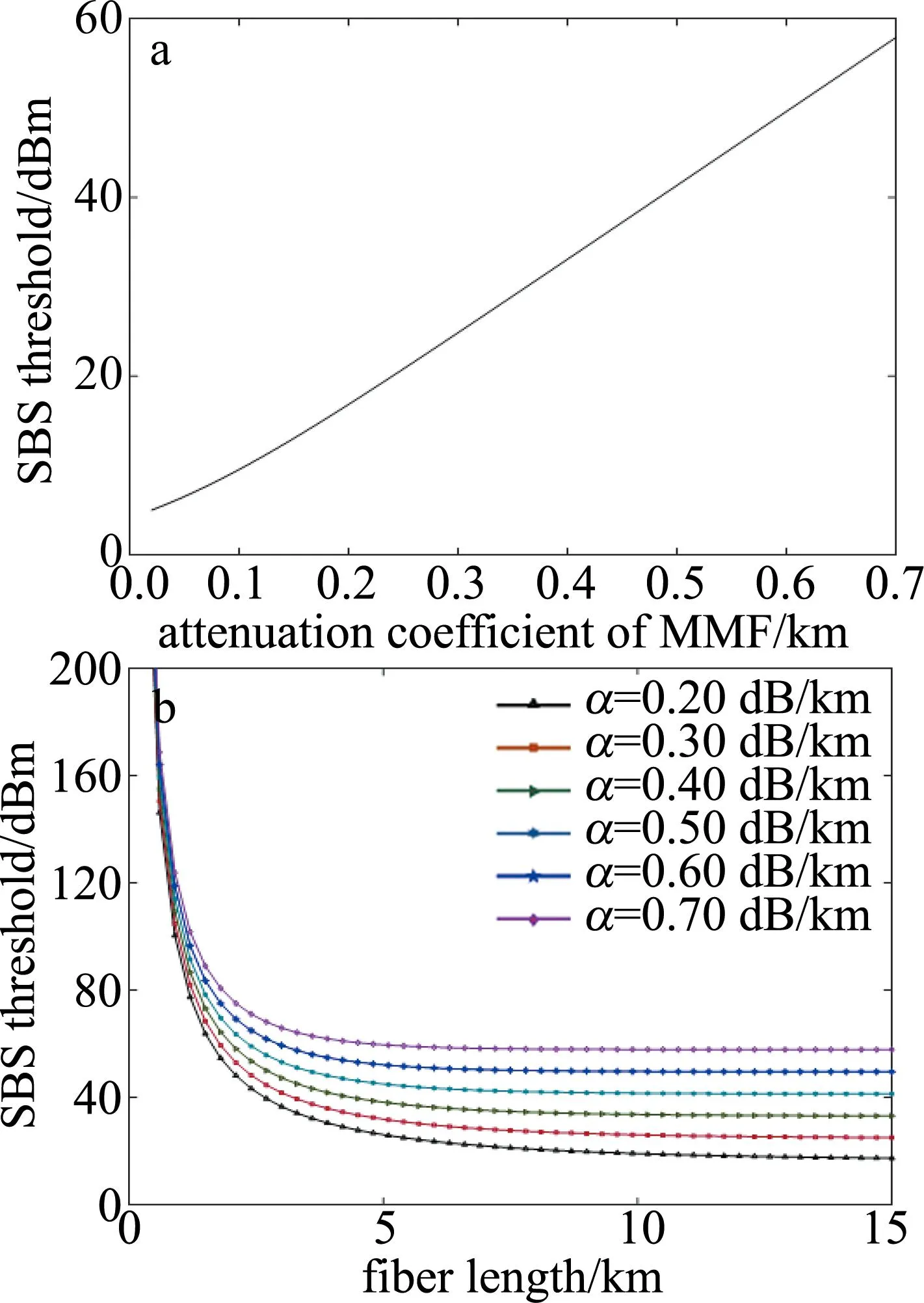
图5 SBS阈值与光纤衰减系数的关系的变化Fig.5 SBS threshold versus fiber attenuation coefficient
从图5b中可以看出,不同衰减系数的耦合环辅助多模光纤SBS阈值随着光纤长度的增加,其阈值衰减速度逐渐变缓,且在趋于一个定值后,随着光纤衰减系数α从0.20 dB/km增至0.70 dB/km,耦合环辅助多模光纤阈值从20 dBm增至60 dBm,与如图5a中结果一致。
3.4 耦合环辅助多模光纤SBS阈值与纤芯半径的关系
由式(4)~式(8)可知,耦合环辅助多模光纤纤芯半径与式(8)中的纤芯有效截面积和阈值增益系数都有关联。根据图1耦合环辅助光纤结构,在一段长为20 km的光纤中,改变最外环纤芯的半径大小,通过式(4)~式(8),数值计算纤芯半径的变化对于耦合环辅助多模光纤SBS阈值的影响。
由图6可知,耦合环辅助阶跃多模光纤SBS阈值随着纤芯半径从0 μm增至35 μm几乎呈指数形式不断增加。
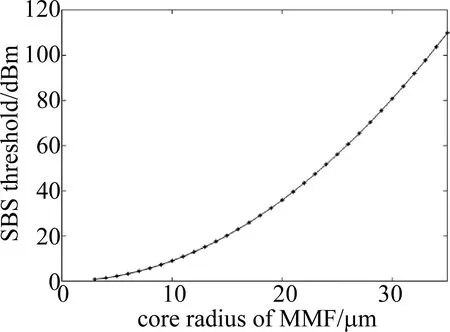
图6 SBS阈值与纤芯半径的关系Fig.6 Relationship between SBS threshold and core radius
4 结 论
由于外界环境及光纤制作缺陷等因素,常规的阶跃型多模光纤在实际的传输中,模间串扰现象会严重影响通信质量。对于此种情况,本文作者设计了一种耦合环辅助多模光纤,优化光纤结构,提升最小模间折射率差值这个关键因素,最终增大差值为原来的1.75倍,平衡了抑制模间串扰与有效模场面积之间的关系。并依据设计的耦合环辅助多模光纤,从理论上和数值上分析光纤有效模场面积、不同阶数模式、衰减系数和纤芯半径对耦合环辅助多模光纤SBS阈值的影响。通过数值计算得到:耦合环辅助多模光纤SBS阈值跟随光纤长度的增加,从急剧下降变至缓慢,最终在18 km左右趋于定值30 dBm;当光纤有效模场面积、不同阶数模式、衰减系数和纤芯半径等参量单个改变时,SBS阈值会随着这些参量的增加而增加。这些规律性的变化可以在设计布里渊分布式光纤传感系统时,为提升系统有效长度和容量提供一定的理论依据。
