宽光谱穆勒矩阵椭偏技术的拓展应用

方慧雯,杨锦宏,章美娟,贺胜男,汪卫华

(安徽大学 物质科学与信息技术研究院,合肥230601,中国)

0 引 言

光谱椭偏技术是一种无损检测技术,通过测量的数据进行反向拟合,得到薄膜的光学常数和厚度[1]。传统的光谱椭偏仪(spectroscopic ellipsometer,SE)只能获得相位差和振幅比这两个测量参数[2]。穆勒矩阵椭偏仪(Mueller matrix ellipsometer,MME)可以获得样品表面的16个穆勒矩阵参数[3],能够对样品的光学性质和结构信息做出一定表述[4]。光谱椭偏技术虽被发现和使用很久,但得益于精密加工、高分辨成像等技术,光谱椭偏在现代科学研究和工业领域仍然应用广泛。光谱椭偏检测技术也在不断发展,如法国国家科学研究中心界面与薄膜物理实验室和设备供应商Nanometrics公司都使用MME对光栅结构的特点进行测量[5]。华中科技大学学者利用MME研究了纳米压印过程中的退偏效应[6],而且还设计了具有高分辨率层析成像性能的MME[7]。ZHENG等人设计搭建了单波长中红外MME,并且误差测量在0.02[8]。国际国内多个公司研发生产出不同型号宽光谱穆勒矩阵椭偏仪,可进行镀膜工艺过程的检测,被广泛运用到集成电路、太阳能光伏、化学等领域[9]。目前椭偏仪已成为表征材料光学常数及薄膜厚度的标准工具[10]。

现有的SE功能和可测参数已经固定,无法用于扩展测量其它的物理参数。但光谱椭偏仪测量的相关偏振参数数据非常丰富,包含了多种物理量信息,通过采用适当的数据处理,可望拓展光谱椭偏仪的应用范围,获得更多的偏振数据和薄膜参数,如薄膜的反射率、透射率,并且能够根据实验需求测量多物理场情况下薄膜的光学常数,甚至测量结构复杂薄膜(例如光栅)的光学常数。本文作者将仿真软件与椭偏测量相结合,以膜厚测量为实例,通过比较仿真软件在不同入射角、不同厚度的Si基底上的SiO2薄膜数据与椭偏测量的实验数据两者之间的拟合程度,验证该方法的可行性。

1 基本原理

1.1 椭偏仪测量原理

以SiO2薄膜为研究对象,结构示意图如图1所示。图中,n1、n2、n3分别为环境/薄膜/基底这三者的折射率;膜厚为d;θ1为环境与薄膜界面的入射角,θ2为经过薄膜发生折射时的折射角(也是薄膜与基底界面的入射角),θ3为光线经过基底产生折射的折射角。

光入射在物体表面时会发生反射与折射,将光波电矢量划分为振动方向平行于入射光面的p光与振动方向垂直于入射光面的s光。由图1可知,入射光在薄膜内多次反射和折射,回到空气介质中的每束光波的振幅和相位都不同,其振幅的大小由菲涅耳公式决定,相邻两束反射光之间的相位差由光程差乘以折射率决定[11],即:

(1)

式中:δ是相邻两束反射光之间的相位差;λ为波长。

因此根据反射系数的定义,p光和s光的总反射率为:

(2)

(3)

式中:r1,p和r1,s是p光和s光在空气和薄膜界面的反射系数;r2,p和r2,s是p光和s光在薄膜与衬底界面的反射系数。

引入参量tanφ描述p光和s光振幅比Ep/Es,Δ表示相位差[12],定义如下式:

f(λ,θ1,n1,n2,k2,n3,k3,d)

(4)

式中:k2为薄膜的消光系数;k3为基底的消光系数。由式(4)可见,椭偏参数φ和Δ可以看作f(·)的函数,与薄膜和衬底的负折射率、厚度有关,即可用椭偏参数反应薄膜的光学常数和膜厚等信息[13]。但通过与仿真软件相结合能够得到更多的偏振信息,如薄膜的反射率、透射率,并且能够根据实验需求测量多物理场情况下薄膜的光学常数,甚至测量结构复杂薄膜(例如光栅)的光学常数。

1.2 穆勒矩阵

S′=MS

(5)

式中:S为入射光的斯托克斯矢量;S′为反射光的斯托克斯矢量;M即为穆勒矩阵[15]。

(6)

2 多物理场光学仿真

多物理场光学仿真可以在单个域模型中容纳多个偏微分方程并进行多物理场的耦合[16]。本文中仿真使用的是几何光学模块,不仅能对光线轨迹追踪还能通过边界条件的改变,来仿真不同情况。为了更好地模拟椭偏仪的测量过程,在软件中构建了椭偏仪内部结构模型,如图2所示。从光源发射宽光谱光经过起偏器变成偏振光;然后再经过第一旋转补偿器后打在样品表面,入射光经过样品反射后通过第二旋转补偿器、检偏器,最后到达探测器。根据实际样品的情况对于模型样品进行设置,先设置基底的材料接着在基底上表面添加薄膜材料,再不断地改变薄膜厚度,直到最后与实际测量曲线拟合成功。本文中实例主要测量膜厚,故在仿真中以膜厚为变量,测量不同的物理参数,可以相应地设其为变量。在建模时所使用的入射光源、光路、样品、测量环境等参数与椭偏仪实际测量时一致。

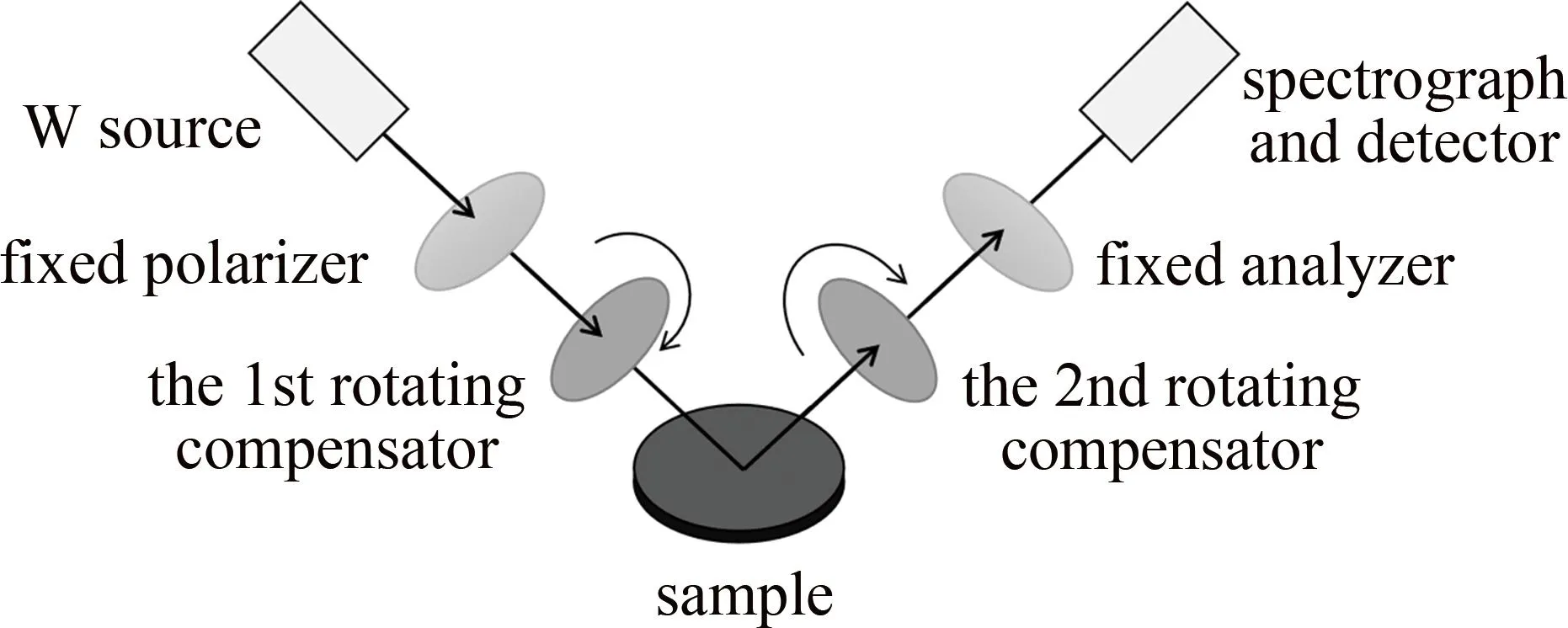
图2 椭偏仪结构示意图Fig.2 Structure diagram of ellipsometer

使用仿真软件建模后,导出不同入射光宽光谱的斯托克斯矢量数据,再根据式(6),通过4组入射光和对应反射光宽光谱的斯托克斯矢量计算样品的宽光谱穆勒矩阵。其中4组入射光初始斯托克斯矢量为:

(7)

式中:S0°代表的是水平偏振光;S45°代表的是45°线偏振光;S90°代表的是垂直偏振光;Sc代表的是圆偏振光;I0为光强。

3 实验与仿真数据对比

实验中使用MP-L穆勒椭圆偏振仪测量Si基底上不同厚度SiO2薄膜样品在不同入射角下的穆勒矩阵。由于SiO2薄膜是各向同性材料,故穆勒矩阵样式如下[17]:

(8)

式中:参数N、C、D的表达式如下:

(9)

式中:φ与Δ是式(4)中的椭偏参数;由式(8)可知,M12与M21数值相等,M33与M44数值相等,M34与M43互为相反数,斜对角的8个参数都为0;且N、C、D不独立,三者关系如下[18]:

N2+C2+D2=1

(10)

本文中用均方误差(mean squared error,MSE)eMSE来判断实验值与仿真值匹配程度的好坏,均方误差数值越小,则两者之间拟合的越好[19]。其定义式如下:

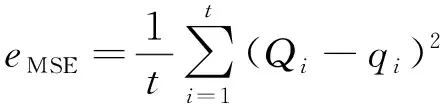
(11)

式中:t是数据个数;Qi是实验值;qi是仿真值。eMSE的值越小,说明实验值与仿真值匹配得越好。通过式(11)进行计算得到eMSE,其最小时所得的厚度即为仿真软件确定的薄膜厚度。

以Si基底上100.0 nm SiO2薄膜的测量为例,实验中入射光入射角为60°、波长范围380 nm～1000 nm,光路如图2所示,测量得到样品的穆勒矩阵。然后利用仿真软件仿真Si基底上SiO2薄膜厚度在100.0 nm附近的反射过程,计算得到不同膜厚的穆勒矩阵。由于SiO2薄膜是各向同性薄膜,采用式(8)的穆勒矩阵,因此只需要比较实验与仿真穆勒矩阵参数的M12、M33、M34,如图3所示。

图3 Si基底上100.0 nm SiO2薄膜实验值及两种SiO2薄膜仿真穆勒矩阵参数对比图Fig.3 Comparison of experimental values of 100.0 nm SiO2 thin film on Si substrate and parameters of two types of SiO2 thin film simulation Mueller matrix

图3中横坐标为波长,纵坐标是归一化后的穆勒矩阵参数值。红色实线是实验测得数值,黑色虚线是105.2 nm SiO2薄膜仿真值,蓝色点划线是100.0 nm SiO2薄膜仿真值。由图3可见,实验数据与厚度为105.2 nm SiO2薄膜仿真数据拟合较好,均方误差值也很小,并且满足各向同性材料的规律,则105.2 nm为仿真确定的薄膜厚度。图3中只列出100.0 nm与105.2 nm仿真结果,实际上做了多个膜厚仿真和计算,因为厚度为105.2 nm时仿真值与实验值的eMSE相对最小,所以为了简洁,图中只列出了两个仿真值进行比较。以下的实验与仿真对比过程中,也是直接列出eMSE相对最小的仿真数据。

3.1 不同入射角对比结果

以上对入射角为60°时实验与仿真结果进行了对比,下面比较实验与仿真的M12、M33、M34在不同入射角时匹配情况。实验测量的样件标定厚度是Si基底上121.8 nm SiO2薄膜,椭偏仪测量该薄膜厚度为122.1 nm。入射角分别为55°,65°,75°,其它参数同图3。通过与图3相同的方法对比不同入射角时实验与仿真的eMSE,如图4、图5、图6所示。120.5 nm为SiO2薄膜厚度最优结果。

图4 入射角55°下M12、M33、M34实验与仿真数据对比图Fig.4 Comparison of M12, M33 and M34 experimental and simulation data at 55° incident angle

图5 入射角65°下M12、M33、M34实验与仿真数据对比图Fig.5 Comparison of M12, M33 and M34 experimental and simulation data at 65°incident angle

图6 入射角75°下M12、M33、M34的实验与仿真数据对比图Fig.6 Comparison of M12, M33 and M34 experimental and simulation data at 75° incident angle

图4、图5、图6中黑色虚线是仿真值,红色实线是实验值,3个图中SiO2薄膜厚度一样,只是在不同入射角下的M12、M33、M34的实验与仿真数据对比。表1中将不同入射角下的M12、M33、M34的实验与仿真数据的均方误差值进行对比,随着入射角的增大,M33的拟合效果变差,这是由于过大的入射角会导致实验误差变大。

表1 不同入射角下M12、M33、M34的实验与仿真数据的均方差值Table 1 eMSE of experimental and simulation data of M12, M33 and M34 at different incident angles

为了更进一步探究入射角对M12、M33、M34的影响,分别测量了Si基底上121.8 nm SiO2薄膜在50°、52°、55°、60°、65°、70°、75°入射角下的M12、M33、M34的数据,并使用仿真软件对这些情况同时进行仿真,得到的实验值与仿真值如图7、图8所示。

图7 不同入射角下121.8 nm SiO2薄膜的M12、M33、M34实验数据图Fig.7 M12, M33 and M34 experimental data of 121.8 nm SiO2 film at different incident angles

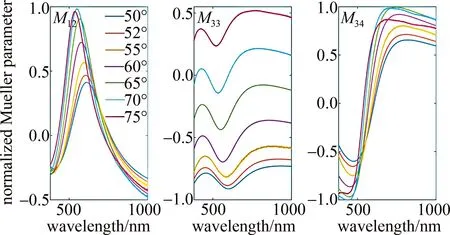
图8 不同入射角下121.8 nm SiO2薄膜的M12、M33、M34仿真数据图Fig.8 M12, M33 and M34 simulation data of 121.8 nm SiO2 film at different incident angles

图7和图8中不同颜色表示不同入射角度,其它参数同图3。由图7、图8可见,不同入射角对M12,M33,M34影响明显,但相同的入射角实验与仿真结果相符度很好,说明在这些入射角范围内进行实验与仿真拟合效果较好。

3.2 不同厚度对比结果

下面对Si基底上3种不同厚度的SiO2薄膜进行实验与仿真对比,其它参数同图3。样品标示SiO2膜厚分别为15.0 nm、100.0 nm、340.0 nm,椭偏仪测量的厚度分别为15.5 nm、101.2 nm、340.6 nm。仿真结果选取eMSE达到最小时,确定的薄膜的厚度分别为16.5 nm、105.2 nm、340.0 nm,在表2、表3、表4中列出了最佳厚度附近的仿真数据与实测厚度的穆勒矩阵参数的eMSE对比值,如图9、图10、图11所示。

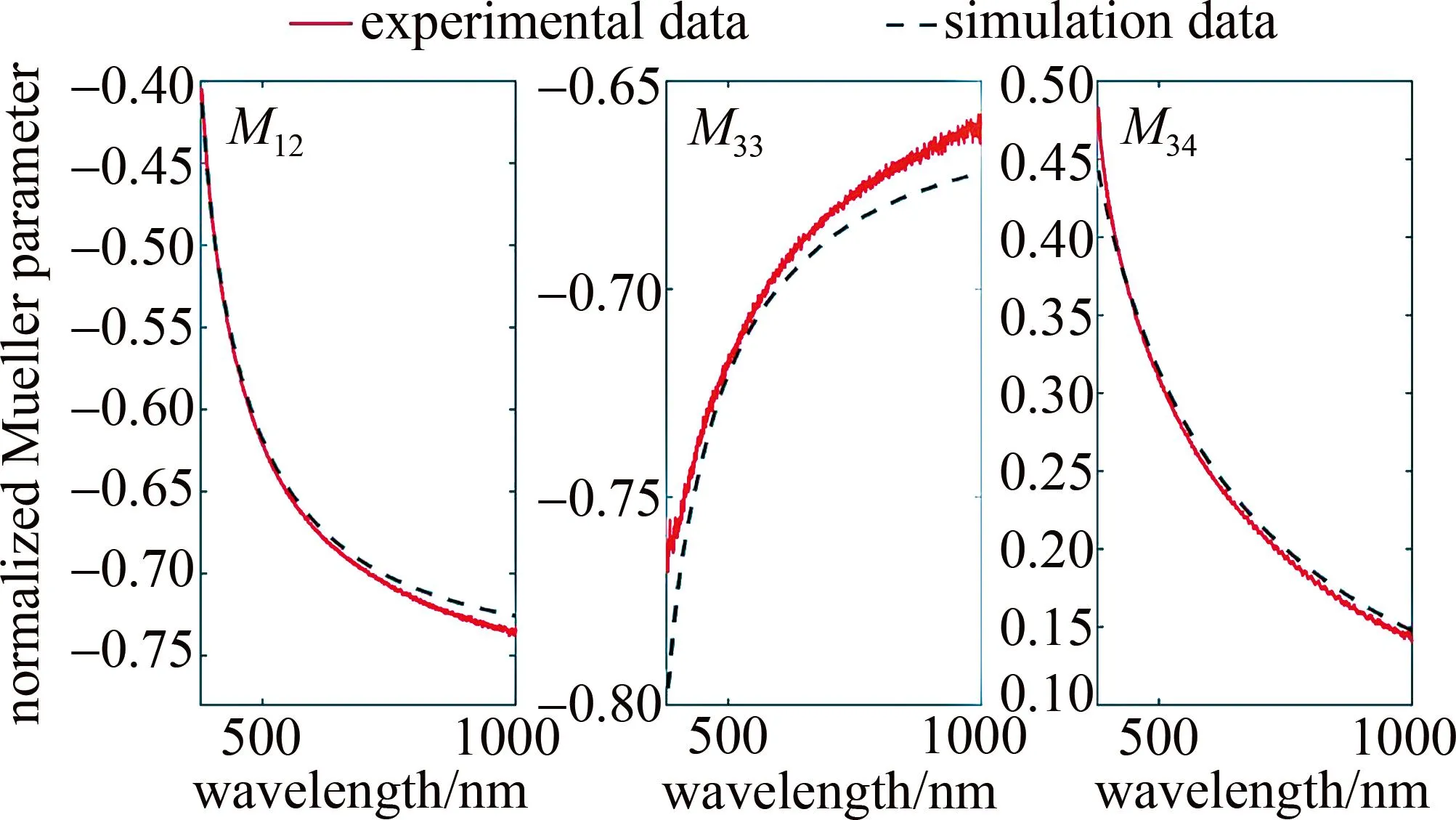
图9 实验测量Si基底上15.0 nm SiO2与仿真的16.5 nm SiO2的M12、M33、M34对比图Fig.9 Comparison between M12, M33 and M34 of 15.0 nm SiO2 on Si substrate and the simulated 16.5 nm SiO2

图10 实验测量Si基底上100.0 nm SiO2与仿真的105.2 nm SiO2的M12、M33、M34对比图Fig.10 Comparison between M12, M33 and M34 of 100.0 nm SiO2 on Si substrate and the simulated 105.2 nm SiO2

图11 实验测量Si基底上340.0 nm SiO2与仿真的340.0 nm SiO2的M12、M33、M34对比图Fig.11 Comparison between M12, M33 and M34 of 340.0 nm SiO2 on Si substrate and the simulated 340.0 nm SiO2

表2 Si基底上15.0 nm SiO2薄膜实验测量与不同厚度仿真的M12、M33、M34的eMSE值Table 2 Experimental measurements of eMSE values of 15.0 nm SiO2 films on Si substrate with different thickness simulations of M12, M33, M34

表3 Si基底上100.0 nm SiO2薄膜实验测量与不同厚度仿真的M12、M33、M34的eMSE值Table 3 Experimental measurements of eMSE values of 100.0 nm SiO2 films on Si substrate with different thickness simulations of M12, M33, M34

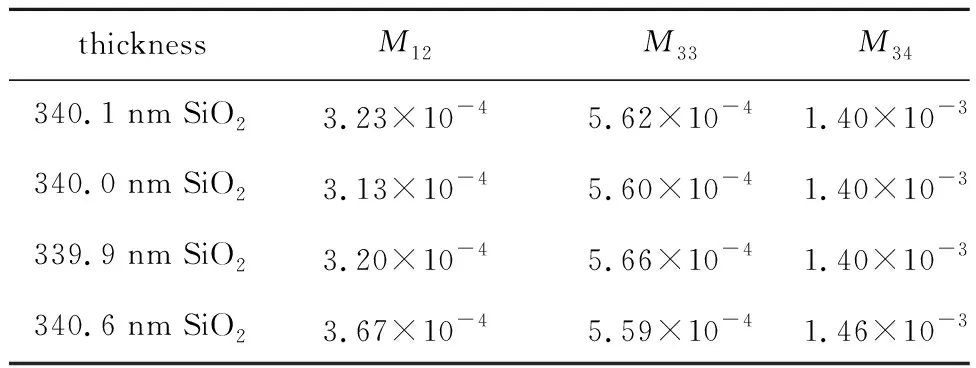
表4 Si基底上340.0 nm SiO2薄膜实验测量与不同厚度仿真的M12、M33、M34的eMSE值Table 4 Experimental measurements of eMSE values of 340.0 nm SiO2 films on Si substrate with different thickness simulations of M12, M33, M34

图9、图10、图11是在入射角同为60°时,不同厚度薄膜实验测得数据和仿真数据的对比。黑色虚线是仿真值,红色实线是实验值。由图9～图11可见,仿真的厚度与实验测量厚度非常接近,总体上各穆勒矩阵参数与实际测量数据的eMSE值都很小。

4 结 论

为了拓展宽光谱椭偏仪的功能,实现更多薄膜参数的测量,提出了椭偏仪实验数据与多物理场仿真相结合实现更多物理量测量的新方法,并以膜厚测量为例进行了验证。通过对Si基底上SiO2膜厚实验测量与仿真得到的穆勒矩阵进行比对,获得了被测样品薄膜的厚度,所得膜厚结果与实际值符合较好。该方法可以实现多物理场环境中(不限于空气中)薄膜参数的椭偏测量。