基于WRF模式高光谱分辨率测温激光雷达系统分析

赵延鹏,卜令兵*,孙博爱,王元庆,林雪飞,梁 琨

(1.南京信息工程大学 气象灾害预警与评估协同创新中心,南京 210044,中国;2.华中科技大学 电子信息与通信学院,武汉 430074;3.贵州省正安县气象局,正安 563400,中国)

0 引 言

激光雷达(light detection and ranging,LiDAR)发射的光子会和大气中的分子发生弹性散射继而产生瑞利-布里渊散射,其构成的卡班斯散射谱线反映了大气温度和压力的波动分布,能够从中解析出大气气体的温度信息[1]。然而大气的瑞利-布里渊散射光谱是分子随机热运动产生的热密度函数,通常通过求解线性玻尔兹曼方程来获得密度波动,但是方程中的碰撞算子解析比较复杂。 1974年,TENTI等人提出了通过6个时刻项来描述碰撞算子的S6模型,时刻项中的参数可以由温度、压力、内热容、导热系数、剪切粘滞系数、体粘滞系数来描述瑞利-布里渊散射的整个光谱包络线[2-3]。该模型的提出,让人们能更贴切地通过一种非解析式形式表征不同温压以及气体环境下的瑞利-布里渊散射光谱。

利用Tenti S6模型解析光谱信息成为了高光谱激光雷达研究的一个新的突破口。1992年,SHE和ALVAREZ等人利用钡分子吸收池滤去气溶胶信号来获取分子散射信号,结合Tenti S6模型反演大气温度得到1 km～5 km的垂直温度廓线,误差为14 K,虽然和探空结果偏差较大,但验证了通过分子散射信号结合Tenti S6模型反演温度理论的可行性[4]。2022年,LIN等人提出了使用菲索干涉仪和多通道光电倍增管(photomultiplier tube,PMT)的高光谱激光雷达测量大气温度廓线,把Tenti S6和干涉式光学鉴频器结合进行30 km以内的大气温度廓线仿真反演[5]。LIN等人的研究得到了相对理论3 K的温度反演误差,但Tenti S6模型对仿真环境的温压场和气体成分较为依赖,他们使用的US76大气模型不具有针对性,这对真实大气瑞利-布里渊散射光谱的展现就存在失真的可能,如将其推广到实验中,使用US76大气模型所得的正演光谱与真实的匹配就会存在误差。另外,LIN等人的研究仅讨论了积分次数对回波光子数的影响,从而影响温度仿真的误差,忽视了US76大气模型下计算所得的回波光子数,不能很好地代表某一特定时空环境下的真实情况,以致仿真结果对系统的搭建缺乏实际指导性。因此,本文作者在其研究基础上对气象场模型进行了优化。

对于中小尺度大气模型,天气预报 (weather research &forecasting,WRF)模式能够通过大气动力学、大气物理学以及大气热力学相关方程进行大气环境的建模,同时选择方案较多、模拟区域较广,能够较好地进行大气温压场的模拟,对于风场、温度场、气溶胶等方面有较好的模拟能力。2021年,XU详细分析了各种大气环境建模方式的优缺点,针对原有大气资源逼真度低且范围小的问题,对WRF模式进行理论研究并生成真实可靠的虚拟大气环境场[6]。同年,TAN综合运用WRF模式数值模拟、激光雷达实测和风洞试验进行超高层建筑的抗风设计研究,验证了结合WRF模式的数值模拟能较好地展现边界层的风场特性,对激光雷达实测具有很好的指导意义[7]。以上二人的研究说明了WRF模式的引入对真实大气环境的展现具有先进性,可以在激光雷达领域进行更多深入的研究。

为了更真实地评估高光谱分辨率测温激光雷达(high spectral resolution LiDAR,HSRL)系统的温度探测能力并提升模拟仿真结果的准确性,本文中使用WRF ver4.2.2模式进行气象场的提取,将用WRF模拟所得的特定大气特征参数代入Tenti S6模型,反演得到0 km～16 km的大气温度廓线,并对比了南京浦口地区不同季节温度反演廓线和随机误差的大小。在激光雷达仿真实验中使用更加贴近实际的大气数据,为后续相关激光雷达相关的实验系统设计提供了参考。

1 研究原理

激光在大气介质中传播会和大气中的分子发生碰撞,产生光散射。大气中的瑞利-布里渊散射源于分子随机热运动自发产生的热密度函数,密度波动会使得介电常数变化,进而使大气折射率发生变化,产生瑞利-布里渊散射现象。瑞利-布里渊散射的介电常数波动Δε在恒密度、忽略温度波动的情况下可以写为下式[8-9]:

(1)

(2)

式中:T为温度,下标T代表恒温;ε为介电常数;ρ为密度,Δρ为密度波动;p为压力,Δp为压力波动,下标p代表恒压;S为熵,ΔS为熵波动,下标S代表恒熵。式(2)等号右边第1项对应布里渊散射下的压强波动,第2项对应瑞利散射下的熵涨落。因此,仿真计算瑞利-布里渊散射光谱时,需要获取较为准确的实际环境的温压,才可以得到和实验更接近的仿真光谱。

挑选使用合适的气象温压场,并结合气象场提供的参数构造出瑞利-布里渊散射谱线,作为实验实测光谱的标准进行拟合,进而反演出大气的温度廓线。本文中的整体系统原理如图1所示。

图1 系统原理框图Fig.1 System diagram

图1展示了温度廓线的反演原理分为两个主要部分:真实大气瑞利-布里渊光谱的获取(灰色)和根据气象场提取信息并计算的理论瑞利-布里渊散射过程(紫色)。真实大气瑞利-布里渊光谱的获取首先需要望远镜接收到大气的瑞利-布里渊散射廓线,所测得的光谱线形是干涉仪仪器函数与散射光的光谱分布函数的卷积:

I1(f)=A(f)*[SR-B(T,p,f)+Nb(f)]+Nd(f)

(3)

式中:f为激光器中心频率;I1(f)为实际测得的光谱;A(f)为干涉仪的仪器函数;SR-B(T,p,f)为大气理想温度T和压力p下的大气瑞利-布里渊散射光谱;Nb(f)为背景光噪声;Nd(f)为探测器噪声;I1(f)为连续光谱,而PMT阵列只能探测到离散的光谱能量。PMT阵列实际测得的采样光谱和I1(f)有以下关系:

I1(f)=fit[I1(Δf)]

(4)

式中:I1(Δf)表示PMT阵列的离散采样点;fit[I1(Δf)]表示利用式(3)对这些离散采样点进行拟合。由此便得到了框图中的实际频谱。

图1中的左侧紫色部分为根据气象场提取信息并计算理论的瑞利-布里渊散射过程,包括理论瑞利-布里渊散射谱线性构造和回波光子数的叠加两步骤。首先是理论线性的构造,根据Tenti S6模型的线性方程组即质量方程和其它6个方程[2],其中包含以下变量:剪切粘滞系数、热传导系数、分子数密度、热速度、平均自由程与激光之比,都是以T、p为变量的物理参数,上述参数中T和p来自外部WRF或者US76提供的温度场数据和气压气象场数据,代入以上参数变量,所得温压相关变量代表了大气模型所得气象场下的大气环境参数,由此构造出根据特定气象场环境下的谱线形。然后计算谱线形对应条件下的回波光子数,地基激光雷达系统接收到的回波光子数可以表示为[10]:

(5)

式中:N(z)是z高度处的回波光子数;h是普朗克常数;c是光速;P(λ)是脉冲峰值功率;Δz是距离分辨率;λ是波长;A是接收望远镜的镜面有效面积;η是系统的光学效率;β(λ,z)是分子和气溶胶的总后向散射系数;α(λ,r)是大气总的消光系数;r是距离的积分变量。

US76和WRF可以为Tenti S6模型提供大气温度场、压力场、分子消光系数、气溶胶消光系数这4个气象场参数, WRF不直接提供大气分子消光系数,可按照经验公式计算得到单个大气分子的瑞利后向散射截面σ1(m2·sr-1)[10]:

(6)

该式使用范围为高度0 km～100 km的混合大气。海拔高度z处单位体积内的分子数目N1(z)为[10]:

(7)

式中:T(z)为使用WRF模式输出的z高度处的大气温度;p(z)为对应的大气压强,同样代入WRF模式的气压产品;Q为温度296 K、压强1.013×105Pa时的单位体积分子数目,取值为2.479×1025/m3。单位体积内所有大气分子的后向散射截面之和,即后向散射系数β1表示为[10]:

β1(z)=N1(z)σ1

(8)

则大气分子消光系数与后向散射系数的关系为[10]:

α1(z)=L×β1(z)

(9)

式中:L为大气分子激光雷达比,设定为8π/3。利用WRF或者US76提供的分子消光系数和气溶胶消光系数,结合激光雷达参数并代入式(5),最终计算得到US76或WRF模拟所得大气环境下的大气回波光子数,叠加背景光子数与散粒噪声光子数后得到完整的理论回波光子数。

将回波光子数与根据WRF或者US76提供的气象场得到的瑞利-布里渊散射光谱叠加,得到理论上由Tenti S6模型计算的理论光谱I2(f),即图1中的理论光谱。

光谱重构时以温度作为自由拟合参数,将实验测得的I1(f)与I2(f)进行最小二乘拟合,根据瑞利-布里渊光谱的匹配度输出对应理论光谱I2(f)下的温度,进而获取理论上的大气的温度廓线,即图1中的温度廓线。为量化系统在不同模型和季节下的随机误差,本文中的温度仿真实验对0 km～16 km高度的廓线结果进行10组平均,即:

(10)

(11)

式中:Nb为背景光子数;Nd为光电倍增管的暗计数;M为累计脉冲数。在夜间时,背景光子数可以近似为0。因此,在保证一定时间分辨率的情况下,尽可能多地叠加脉冲次数会提升信噪比。

2 系统合理性验证

为了验证不同大气场模型对激光雷达工作环境反映的真实可靠性,本文中选取了WRF ver4.2.2大气模型和US76大气模型,结合德国大气物理研究所研制的小型瑞利自主激光雷达(compact Rayleigh autonomous LiDAR,CORAL)的技术参数计算了0 km～40 km以内的大气回波光子数廓线,并将两种模型计算下的大气回波光子数与参考文献中的实验结果做了对比,进行不同模型温压场的适用性参考[11]。其中WRF ver4.2.2模式初始场和边界场使用的是美国国家环境预报中心数据集 (National Centers for Environmental Prediction final,NCEP FNL)0.25°×0.25°的6 h再分析资料,覆盖面积为:1359 km×1440 km,624 km×561 km,220 km×202 km;长波辐射与短波辐射传输方案为RRTMG Shortwave and Longwave Schemes方案[12-14];边界层参数化方案为Yonsei University Scheme方案[15-16];第1层嵌套积云参数化方案采用Grell-Freitas Ensemble方案[17-18],第2、第3层嵌套关闭积云参数化方案,3层云微物理参数化方案为HUJI SBM (full)方案[19-20]。表1为模式的主要输入参数。表中,UTC表示协调世界时(universal time coordinated)。CORAL的技术参数如表2所示[11]。

表1 WRF模式的输入参数Table 1 Input parameters of WRF

表2 CORAL实验系统参数Table 2 CORAL system parameters

得到的结果如图2所示。图2中,simulation 1是基于US76模型下得到的回波光子数,simulation 2是基于WRF模式下得到的回波光子数,observation是CORAL的第三通道实验数据,10 km以下的几何重叠区域已扣除。

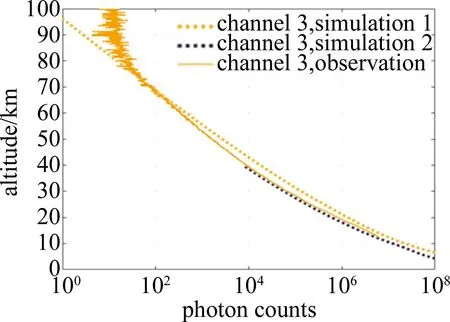
图2 CORAL系统回波光子数Fig.2 Echo photons of CORAL

由于WRF模式参数化方案的限制,模式顶气压设置上限为300 Pa,所以图2中只给出了40 km到地面的回波光子数。两种模型计算所得的回波光子数差如图3所示。由图2、图3可知,在10 km～40 km范围内基于WRF模式得到的温压场因其更接近实验真实环境,所以得到的仿真结果较US76模型得到的实验结果与实验数据更吻合。随着高度的上升,两种模型的回波光子数逐渐减少,但基于US76模型下得到的回波光子数下降速率更快,信噪比相应下降地更快,而基于WRF模式下得到的信噪比相比下降地较慢。因此,使用WRF模式得到的温压场在环境构造上有着更高时空真实性的优势,利用其得到的气象场要素代入Tenti S6模型内会更贴近地引入准确的回波光子数,并降低与实验的误差。

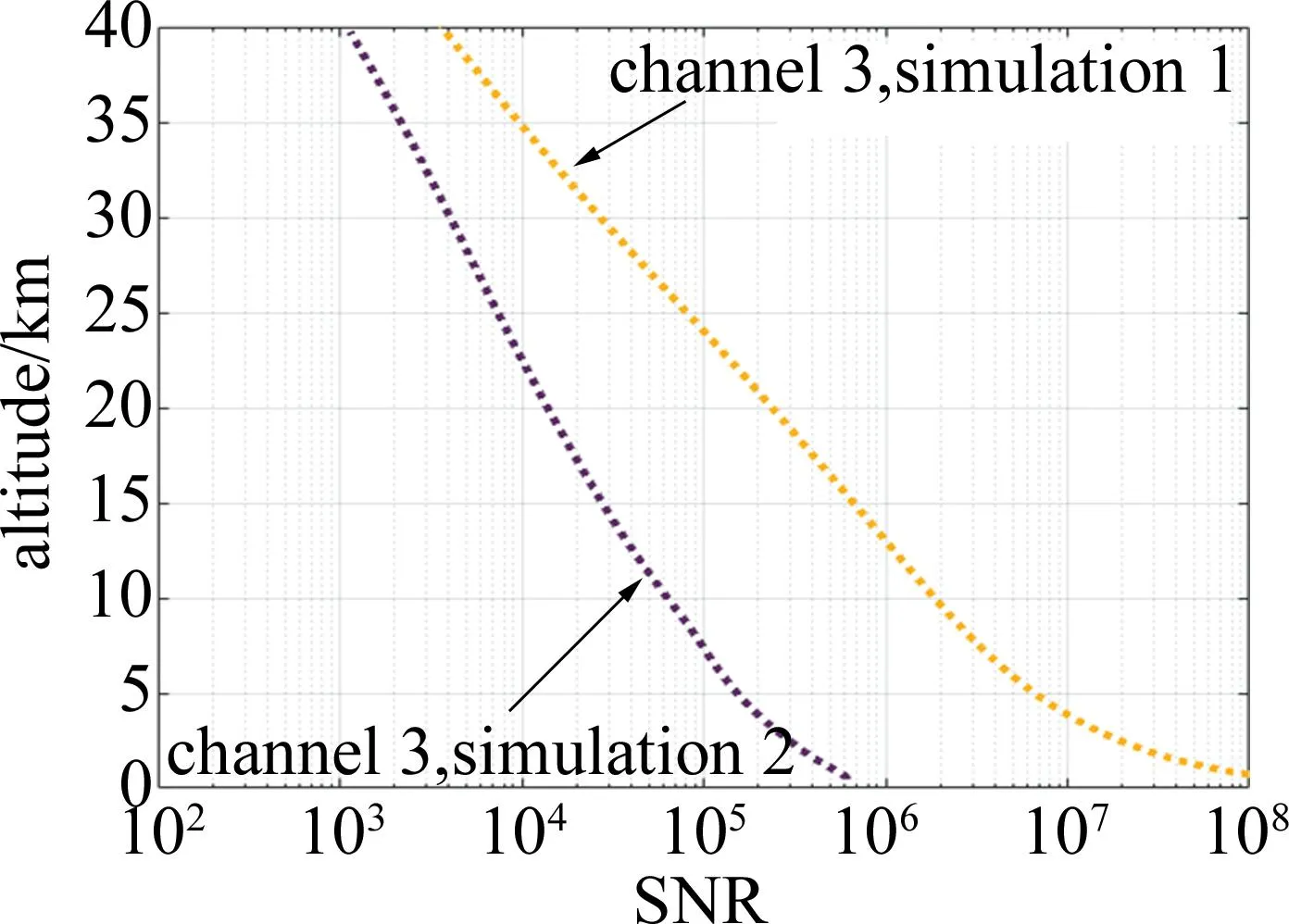
图3 CORAL信噪比对比Fig.3 Difference of CORAL SNR

3 温度及误差仿真结果

对于温度廓线的仿真,采用表1中的WRF边界场、初始场以及微物理、积云方案和嵌套输入参数,将中心区域改为南京市浦口区(118°E, 32.2°N),对以下几个季节环境时间点春(2021-03-19T16:00—2021-03-20T16:00 UTC)、夏(2021-06-20T16:00—2021-06-21T16:00 UTC)、秋(2021-09-22T16:00—2021-09-23T16:00 UTC)、冬(2021-12-20T16:00—2021-12-21T16:00 UTC)无强降水和深厚低云4个日期进行模型的温压场搭建。表3为来自“reliable prognosis”的4个日期20:00时的天气现象记录。表中cloud amount为云量(无量纲),H为云高。

表3 选取日期天气现象Table 3 Date weather

图4为两种模型的温度廓线与该地区对应时间点20:00时探空数据的对比。从图4可知,在0 km～16 km范围内,温度廓线的变化趋势WRF模式的输出产品与该地区该时刻的探空数据保持着较好的一致性,同时在数值上也较US76模型更接近探空数据。

图4 不同季节时间点下的温度场对比Fig.4 Comparison of temperature fields at different seasonal time

两种模型的气压廓线与该地区对应时间点的探空数据对比如图5所示。从图5可知,3种模型在0 km～16 km的气压廓线变化趋势和数值都较温度廓线一致性高,在数值上WRF的输出产品比US76更为接近探空数据一点,综上所述,采用本文中所选方案的WRF产品输出温压场较US76大气模型和探空更为接近,可以认为在该晴空、无强干扰的情况下可以为干涉式HSRL系统提供一个较好的仿真计算用模拟大气环境。

图5 不同季节时间点下的气压场对比Fig.5 Comparison of pressure fields at different seasonal time

本文作者设计的一套干涉式大气瑞利-布里渊散射采集激光雷达系统,参数如表4所示。

表4 实验系统参数Table 4 Experiment system parameters

由式(11)可知,信噪比与累计脉冲数的二分之一次方成正比,在讨论不同的季节与气象场的差异引起的回波光子数之前,需对累计脉冲数进行讨论。

图6为春季15 km高度处不同积分次数下的瑞利-布里渊散射光谱。其中绿线为积分10次的光谱,红线为积分100次的光谱,蓝线为积分10000次的光谱。由图6可知,随着积分次数的变多,瑞利-布里渊散射光谱的还原度逐渐提高,在10次积分的情况下,瑞利-布里渊散射光谱被噪声淹没,几乎难以辨认。在积分次数达到10000次时,可以清晰地分辨出瑞利-布里渊散射光谱。因此本文中后续的仿真实验都基于10000次脉冲积分进行。

图6 春季15 km不同积分次数下的瑞利-布里渊光谱Fig.6 Rayleigh-Brillouin spectrum of different times pulse in 15 km spring

结合US76模型计算所得的回波光子数和结合WRF计算所得的回波光子数如图7所示。图7中红线、蓝线、绿线、粉线分别为结合WRF模式10000次脉冲积分所得春季、夏季、秋季、冬季的回波光子数。

图7 WRF和US76的回波光子数Fig.7 Echo photons of WRF and US76

青线为结合US76模型气象场经过10000次脉冲积分的回波光子数,因江苏南京浦口地区4个季节下的分子、气溶胶种类和垂直密度在实际情况下有不同的分布,4个季节下使用结合WRF模式所得的回波光子数存在差异。因为结合US76模型计算所得的回波光子数不存在季节差异,所以只有一条线。

使用两种模型计算的回波光子数在不同季节的差如图8所示。图8中红线、蓝线、绿线、粉线分别为结合WRF模式计算的回波光子数与结合US76模型计算所得的回波光子数在春季、夏季、秋季、冬季的绝对差异。从图中可以看出,两种模型计算的回波光子数夏冬两季时在12 km处相等,春季和秋季分别在12.9 km、13.3 km处相等。

图8 WRF与US76回波光子数差Fig.8 Echo photons difference of WRF and US76

随着高度上升,两种模型计算所得回波光子数逐渐由WRF大于US76转变为US76大于WRF。两种模型计算所得的信噪比如图9所示。图9中蓝线、红线、绿线、粉线为结合WRF模式所得春季、夏季、秋季、冬季经过10000次积分的信噪比廓线,青线为结合US76模型经过10000次积分所得信噪比廓线。由图9可知,信噪比和回波光子数有一致的变化趋势,同样符合随高度衰减的特性。当积分次数在10000次时,16 km处结合WRF模式的信噪比为100,略低于结合US76模型所得信噪比,但在0 km～12 km处结合WRF模式计算所得信噪比大于US76模型。

图9 WRF和US76的信噪比Fig.9 SNR of WRF and US76

由光谱反演得到的温度随机误差如图10所示。图10中蓝线、红线、绿线、青线分别为结合WRF模式积分10000次所得的春季、夏季、秋季、冬季的随机误差,粉线为结合US76模型积分10000次所得的随机误差。由图10可知,16 km以下结合WRF模式所得的反演温度廓线随机误差为:春季不超过0.65 K;夏季不超过0.98 K;秋季不超过0.59 K;冬季不超过0.63 K。结合US76模型计算所得16 km以下温度随机误差无季节特征最大不超过1.1 K。图中两种模型的随机误差相差最大的地方在10 km处,有0.3 K。因在12 km以下WRF计算所得的回波光子数大于US76计算所得,图8中粉线代表的随机误差大于其它4条线。随着高度逐渐升高,回波光子数逐渐减少。同时两种模型计算所得回波光子数大小关系转变后,两种模型的随机误差廓线逐渐靠拢同时不确定度增加。从图5中两种模型计算所得的回波光子数可以看出,结合WRF模式所得的回波光子数在南京浦口地区随高度衰减速度较快,而结合US76模型所得的回波光子数随高度衰减较慢,此特征反映在图10中为结合WRF模式所得的四季随机误差在0 km～16 km的增速要比结合US76模型快。由此,基于菲索干涉仪和PMT阵列探测大气瑞利-布里渊散射光谱的地基激光雷达系统进行温度反演,在南京浦口地区无强降水和深厚低云的天气环境下,探测能力最强的地方应当是16 km以下的低空,随机误差小于0.98 K。随着探测高度的继续升高,反演温度的随机误差会突破1 K。

图10 WRF和US76产生的随机误差Fig.10 Random error of WRF and US76

4个季节下的温度仿真结果如图11所示。图11中,红线、绿线、蓝线、粉线为结合WRF模式仿真计算的春季、夏季、秋季、冬季0 km～16 km温度仿真廓线,黑线为结合US76模型仿真计算所得。由于US76大气模型较为单一,任何季节的反演温度都是一致的,综合来看,结合WRF模式仿真计算的温度仿真廓线更能代表特定地区的不同季节环境下的温度场信息,且温度随高度变化与实际变化一致。

综上可知,利用积分次数达到10000次还原出的瑞利-布里渊散射光谱,16 km以内的温度仿真可以得到较好的结果。证明基于Tenti S6模型拟合大气瑞利-布里渊散射光谱反演大气温度廓线具有可行性。结合WRF模式输出的气象场的反演方法,对开展其它地区HSRL系统观测应用研究,有积极的参考意义。

4 结 论

从解析大气瑞利-布里渊散射光谱并反演0 km～16 km的温度需求出发,对基于光电倍增管阵列采集经过菲索干涉仪的HSRL在不同季节的温度反演能力及系统误差进行了评估。结果表明:在结合Tenti S6模型进行瑞利-布里渊光谱拟合的情况下,常规的US76大气模型不具备针对性和代表性,在具体时空位置的大气要素场反演具有一定的局限性;WRF模型系统的数据源对某一特定时空要素场具有更贴近真实的表现,同时在设置上更为灵活方便,在无强降水和深厚低云的天气条件下,对于实际瑞利-布里渊回波光谱的展现也更准确。在经过10000次脉冲平均后,16 km以下结合WRF模式所得的反演温度廓线随机误差为:春季环境下不超过0.65 K;夏季环境下不超过0.98 K;秋季环境下不超过0.59 K;冬季环境下不超过0.63 K。相关研究对未来多通道高光谱雷达系统的设计与优化具有一定参考意义。