多芯激励下实际多芯光纤芯间串扰特性研究
2023-01-08向练潘洪峰金树林邵卫东
向练,潘洪峰,金树林,邵卫东
(1.苏州大学光通信网络技术重点实验室,江苏 苏州 215006;2.苏州大学电子信息学院,江苏 苏州 215006)
0 引言
为了解决未来高速增长的通信容量需求问题,基于空分复用原理的多芯光纤(MCF,multi-core fiber)技术应运而生[1-3]。然而,多个纤芯之间存在的芯间串扰(ICXT,inter-core crosstalk)现象(本文简称为串扰),会极大地影响光纤通信的质量。因此,对MCF 的串扰特性研究是广泛应用MCF 传输系统的前提。
多芯光纤串扰特性的理论研究主要运用耦合模理论和耦合功率理论[4-8]。基于耦合模理论,Hayashi 等[9]提出了匀质弱耦合多芯光纤中串扰随距离纵向变化的离散变化模型(DCM,discrete change model),该模型是研究同质MCF 的经典模型,但不适用于异质MCF 的非相位匹配区。随后改进的离散变化模型[10]被提出,解决了这一局限性。Wang 等[11]提出一种通用半解析模型,该模型最大的特点是可以反映光纤内在物理参数对芯间串扰的影响,但是由于其串扰是通过多段累加计算获得的,因此其计算耗时较长。此外,考虑实际光纤铺设场景,Marcuse[12]提出了耦合功率理论。由于弯曲和扭转扰动的存在,光纤在传输一段距离后,其功率趋于动态平衡状态。此后,Koshiba 等[13-14]对功率耦合系数进行重新定义,在传播常数差中加入了弯曲和扭转扰动,并且对扭转进行积分得出平均功率耦合系数,在与实验数据对比中得到指数自相关函数更适合模拟扰动的平稳随机过程的结论。此外,Macho 等[15-16]将耦合模理论和耦合功率理论推广到非线性领域,建立了线性和非线性串扰的统一模型。该模型包含弯曲和扭转扰动,并与实验结果对比,进行均值、方差和相位匹配点数量的统计分析。以上对串扰特性的研究都是基于单输入下的多芯光纤,即单芯激励的情况,对多芯激励下多芯光纤串扰特性的研究工作还很少[17-18]。汪文杰等[18]对多芯激励下的串扰特性进行了研究,将多芯激励下的多芯光纤拆分成多组单芯激励的双芯光纤,通过线性叠加获得了多芯激励下的串扰评估。这种近似处理方法虽然在一些特定条件下对弱耦合多芯光纤是适用的,但是在外部随机扰动影响下与实际多芯激励的情况存在一定的偏差,限制了其适用范围。
本文基于耦合功率理论,采用中心对称结构的七芯光纤模型,得到简化后的七芯光纤功率耦合方程,针对实际多芯光纤模型,推导了3 种多芯激励情况下各纤芯的光功率和ICXT 的解析表达式,并根据表达式研究多芯激励下归一化功率和ICXT 随距离的变化关系。研究发现,经过长距离传输后,在外界随机扰动的影响下,各纤芯的归一化功率都会收敛到一个定值,达到动态平衡状态,并且其收敛距离随着弯曲半径的增大呈指数级减小,逐渐趋于一个定值。此外,还研究了多芯激励和单芯激励的关系,在多芯同时激励和分别激励下推导其功率和ICXT 解析表达式,并在仿真分析中得出多芯激励的本质特性,即多芯激励对串扰的贡献是不相关的,多芯激励的串扰可以等同于每个激励纤芯单独激励时串扰的线性叠加。
1 多芯激励下串扰评估模型
在多芯光纤串扰特性研究中,为了减少不必要的相位等信息,本文采用耦合功率理论进行串扰估计。此处考虑纤芯间距大于4 倍纤芯半径时的弱耦合情况,忽略光纤传输的衰减、色散和非线性效应的影响,也忽略纤芯的自耦合影响和纤芯间的交叉耦合影响,此时纤芯m中功率Pm可表示为[19]

其中,(xm,ym)为纤芯m的坐标,(xn,yn)为纤芯n的坐标;Rb为弯曲半径;Δβmn=βm-βn为纤芯m和纤芯n之间的固有传播常数差,其中βm和βn分别为纤芯m和n的无扰传播常数。
本文根据以上功率耦合方程组,以七芯光纤模型为例进行串扰评估,七芯光纤截面如图1 所示,除了中间纤芯外,外部6 根纤芯呈正六边形分布。
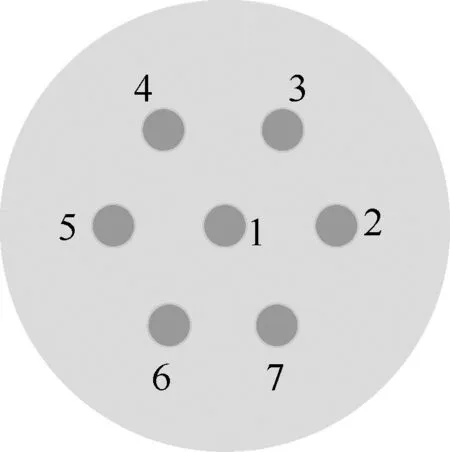
图1 七芯光纤截面
如图1 所示,假设中间纤芯1 和外部纤芯2~7之间的功率耦合系数相同,记为h,外部纤芯m和n之间功率耦合系数为kmn。假设相邻纤芯的功率耦合系数相等,即kmn=knm,并且根据光纤的对称结构假设k23=k27,k24=k26。根据以上假设,主要功率耦合系数参数为h、k23、k24和k25。则式(1)功率耦合方程在七芯光纤中的具体形式可以表示为[22]

以图1 所示的七芯光纤进行研究,考虑3 种多芯激励情况,如图2 所示。其中,激励纤芯指的是需要注入光功率的纤芯,耦合纤芯指的是不注入功率,只进行耦合的纤芯。情况1 表示纤芯2、4、6为激励纤芯,纤芯1、3、5、7 为耦合纤芯;情况2表示纤芯1、3、5、7 为激励纤芯,纤芯2、4、6为耦合纤芯;情况3 表示纤芯2~7 为激励纤芯,纤芯1 为耦合纤芯。

图2 3 种多芯激励情况
在情况1 中,基于式(7)~式(13)的七芯光纤的功率耦合方程,从纤芯2、4、6 注入光信号,采用归一化功率,即功率耦合方程的初值为P1=P3=P5=P7=0,P2=P4=P6=1,可以得到各纤芯中光功率的解析解为

在情况2 中,从纤芯1、3、5、7 注入光信号,采用归一化功率,即功率耦合方程的初值为P1=P3=P5=P7=1,P2=P4=P6=0,与情况1 相反,可以得到各纤芯中光功率的解析解为
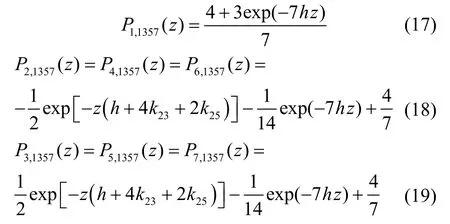
其中,Pn,1357(z)表示经过纤芯1、3、5、7 注入功率,传输距离z后纤芯n的功率。
在情况3 中,从纤芯2~7 注入光信号,采用归一化功率,即功率耦合方程的初值为P1=0,Pn= 1,n≠ 1,可以得到各纤芯中光功率的解析解为
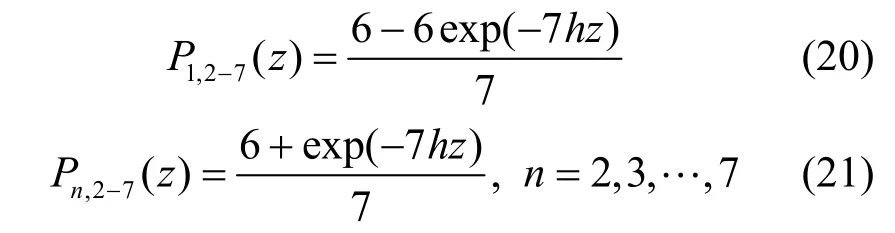
其中,Pn,2-7(z)表示经过外部纤芯2~7 注入功率,传输距离z后纤芯n的功率。
在多芯激励多芯光纤系统中,某一纤芯的串扰是指激励纤芯同时激励时对该纤芯耦合的功率与耦合纤芯同时激励时自身的功率之比[9]。因此,对于情况1 中各耦合纤芯的串扰可以表示为
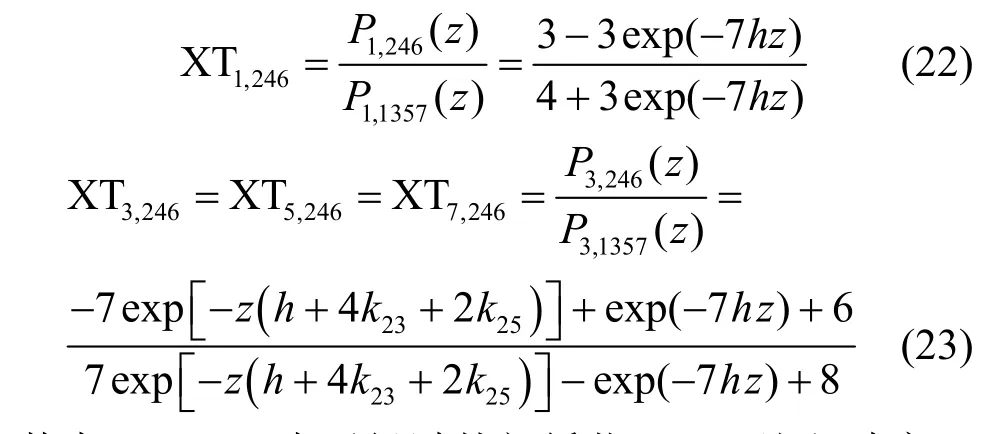
其中,XTn,246表示经过外部纤芯2~7 注入功率,传输距离z后对纤芯n的芯间串扰。
对于情况2 中各耦合纤芯的串扰可以表示为

其中,XTn,1357表示经过外部纤芯1、3、5、7 注入功率,传输距离z后对纤芯n的芯间串扰。
对于情况3 中耦合纤芯1 的串扰可以表示为

2 仿真验证及串扰特性分析
本节将根据以上多芯激励下多芯光纤的串扰评估模型,通过仿真研究3 种多芯激励情况下归一化功率和串扰随传输距离的变化情况,进而研究其串扰特性,并在串扰特性分析的基础上,深入探究多芯激励的本质特性。仿真设定的MCF 是完全同质的,各纤芯的无扰传播常数相等,主要实验参数如表1 所示。

表1 七芯阶跃型同质多芯光纤的主要实验参数
2.1 3 种激励情况的串扰特性分析
本文第1 节推导了3 种多芯激励情况下纤芯的功率和串扰评估模型。在情况1 下进行仿真,得到如图3所示的归一化功率和芯间串扰与传输距离的关系。
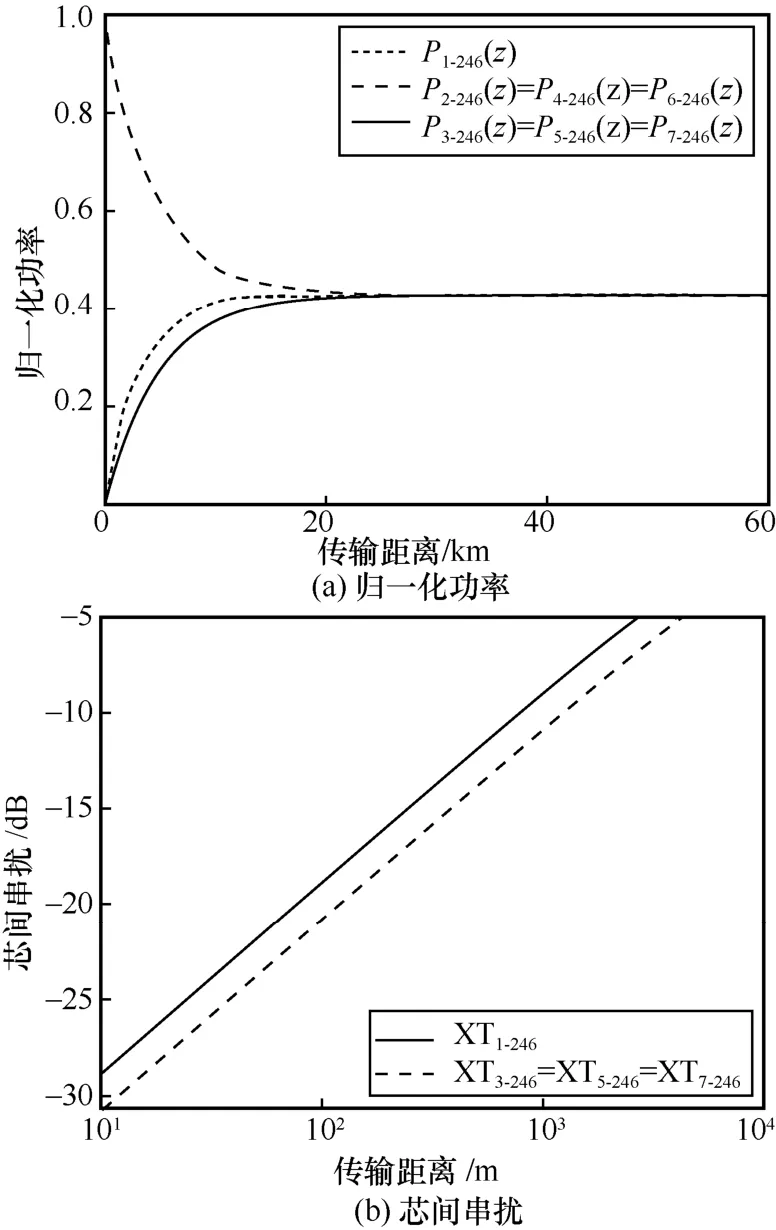
图3 纤芯2、4、6 激励下归一化功率和芯间串扰与传输距离的关系
如图3(a)所示,在纤芯2、4、6 激励时,纤芯2、4、6 的归一化功率相等且随传输距离的增加呈指数级减小,而纤芯1、3、5、7 的归一化功率随传输距离的增加呈指数级增加,最后所有纤芯的功率都趋于一致。需要指出的是,由于光波传输时功率一直处于波动状态,其功率趋于一致不代表功率值不变,而是处于动态平衡的状态。在功率趋于一致前,纤芯1 的功率比纤芯3、5、7 的功率大。从图3(b)可以看出,虽然纤芯1 和纤芯3、5、7 的串扰都随传输距离的增加而增加,但是纤芯1 的串扰一直都比纤芯3、5、7 的串扰大。究其原因,在七芯光纤的纤芯分布中,纤芯1 处于纤芯2、4、6 的中间,而纤芯3、5、7 处于周边,在纤芯2、4、6激励时,纤芯1 距离纤芯2、4、6 的相对距离总和较近,因此会造成更大的串扰。纤芯排布的中心对称结构与激励纤芯的对称分布是导致纤芯3、5、7和纤芯2、4、6 的功率相等的原因。
对于情况2 和情况3,归一化功率和芯间串扰与传输距离的关系如图4 和图5 所示。情况2 与情况1 相反,激励纤芯和耦合纤芯互换,其归一化功率和串扰变化情况和情况1 分析类似,只是激励纤芯1 的归一化功率相比于纤芯3、5、7 的归一化功率下降得更快,主要是因为激励纤芯1 与耦合纤芯2、4、6 的相对距离较近,对耦合纤芯的功率耦合更强,从而导致功率下降更快。对于情况3,其归一化功率和串扰特性与前2种情况一致。在纤芯2~7 激励下,纤芯1 的耦合功率增加很快,其串扰增加得也很快。在多芯(六芯)激励下,只有中间纤芯为耦合纤芯,其耦合功率值刚好是单芯激励情况时耦合功率值的6 倍。
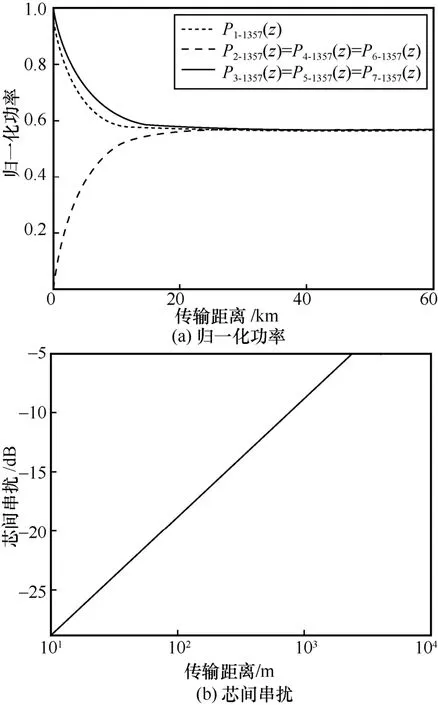
图4 纤芯1、3、5、7 激励下归一化功率和芯间串扰与传输距离的关系
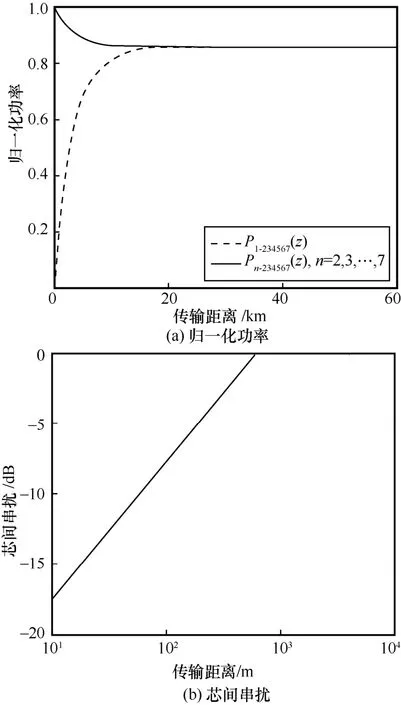
图5 纤芯2~7 激励下归一化功率和芯间串扰与传输距离的关系
外部随机扰动对MCF 的串扰的影响因素主要有弯曲和扭转。本文基于耦合功率理论的串扰估计模型在扭转率上取积分平均,因此扭转扰动的影响取平均值,不体现在最终的串扰估计中。而弯曲扰动会对串扰造成较大的影响,在相位匹配区和非相位匹配区,串扰的差值超过10 dB[4]。因此,本文研究了弯曲半径对多芯激励下多芯光纤芯间耦合的影响。图6 为纤芯2、4、6 激励下弯曲半径Rb分别为200 mm 和500 mm 下的归一化功率与传输距离的关系。当弯曲半径为200 mm时,其收敛点在33.3 km 处;当弯曲半径为500 mm时,收敛点在13.7 km 处。从图6 可以看出,当弯曲半径变化时,其归一化功率趋于一致的距离是不一样的。其主要原因是弯曲半径会造成芯模耦合的相位失配,从而影响其归一化功率的收敛距离。图7 为归一化功率的收敛距离与弯曲半径的关系。从图7 可以看出,随着弯曲半径的增大,收敛距离呈指数级减小,并且逐渐趋近于一个恒定值。该恒定值为没有弯曲影响下水平放置光纤的收敛距离。

图6 纤芯2、4、6 激励下归一化功率与传输距离的关系
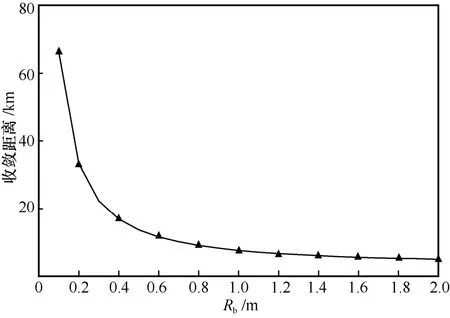
图7 归一化功率的收敛距离与弯曲半径的关系
2.2 多芯激励下串扰的本质特性分析
以上多芯激励多芯光纤串扰特性的研究说明了多芯光纤多芯激励下的光功率和串扰变化情况。通过分析图5 可知,在周边六根纤芯的激励下,中间纤芯的耦合功率大小是在单芯激励情况下的6 倍。由此是否可以推测多芯激励下对周边纤芯的耦合是每个激励纤芯分别耦合之和?本节将会对此进行深入研究。以图2 中情况1 和情况3 为例,分别计算同时激励和分别激励情况下的功率和串扰分布。
在情况1 中,纤芯2、4、6 为激励纤芯,其他纤芯为耦合纤芯。以对纤芯1 进行耦合为例,当只有外部纤芯2 激励时,纤芯1 的归一化功率记为P1,2(z)。同样,由于纤芯的中心对称分布,当只有纤芯4、6 分别激励时,纤芯1 的归一化功率和P1,2(z)相等。对七芯光纤功率耦合方程 式(7)~式(13)代入初值P2(0)=1,Pn(0)= 0,n≠ 2,求解可以得到

纤芯2、4、6 同时激励时纤芯1 的耦合功率P1,246(z)如式(14)所示,根据式(14)和式(26)可知,纤芯2、4、6 同时激励时对纤芯1 的耦合功率是分别激励时之和,即P1,246(z)=P1,2(z) +P1,4(z) +P1,6(z)。由此可以看出,多芯激励情况下可以等效于每根激励纤芯分别激励时对其他纤芯的耦合。上述是对中间纤芯1 耦合的分析,为了普遍分析这个结论的适用性,对于周边纤芯3 的耦合进行同样的分析。对于七芯光纤模型,根据功率耦合方程,在纤芯2激励下,耦合功率和串扰分别为

其中,P3,2(z)和P2,2(z)分别表示在纤芯2 激励时纤芯3 和纤芯2 中的功率变化情况;XT3,2表示纤芯2激励时对纤芯3 耦合的串扰。以下标记表示同样含义,不再赘述。
在纤芯4 激励下,由于纤芯4 和纤芯2 关于纤芯3 呈对称分布,因此纤芯3 的耦合功率和串扰和纤芯 2 激励时结果一样,即P3,4(z)=P3,2(z),XT3,4=XT3,2。
在纤芯6 激励下,纤芯3 的耦合功率和串扰分别表示为
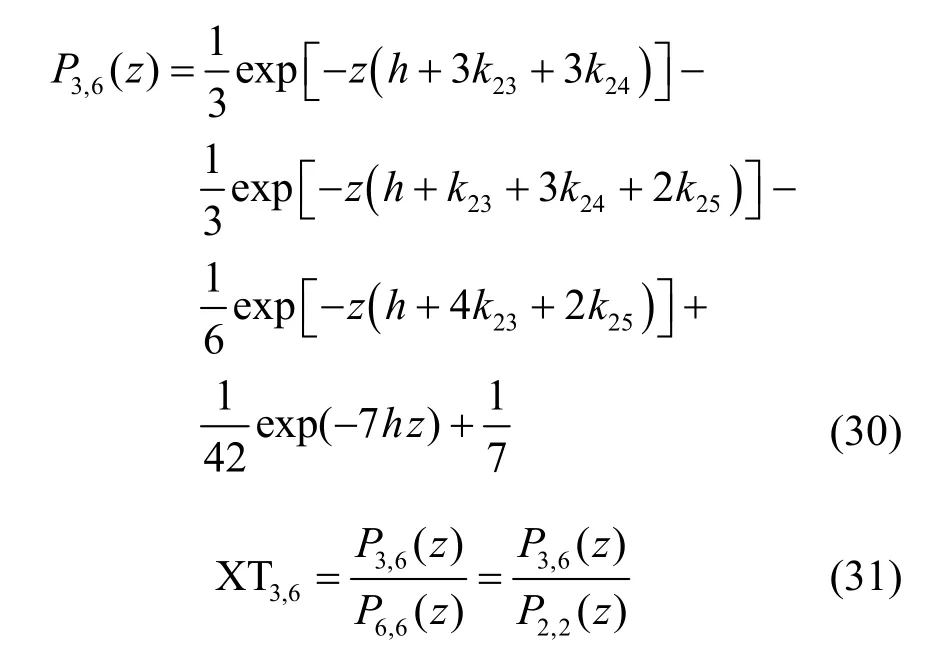
在纤芯2、4、6 同时激励下,纤芯3 的耦合功率和串扰分别由式(16)和式(23)表示。
基于以上分析,本文在纤芯2、4、6 分别激励和同时激励情况下进行了仿真,其归一化功率和芯间串扰与传输距离的关系如图8 所示。图8(a)中,P3-2(z) +P3-4(z) +P3-6(z)表示纤芯2、4、6 分别激励时对纤芯3 耦合的功率之和,P3-246(z)表示纤芯2、4、6 同时激励时对纤芯3 耦合的功率。从图8(a)中可以看出,纤芯2、4、6 分别激励时对纤芯3耦合的功率之和与纤芯2、4、6 同时激励时对纤芯3 耦合的功率相等,即P3-246(z)=P3-2(z) +P3-4(z)+P3-6(z)。图8(b)中,XT3-2+XT3-4+XT3-6表示纤芯2、4、6 分别激励时对纤芯3 耦合的串扰之和。同样可以看出,纤芯2、4、6 分别激励时对纤芯3 耦合的串扰之和与纤芯2、4、6 同时激励时对纤芯3耦合的串扰几乎重合,其不完全相等的原因是单芯激励和多芯激励的串扰计算式有所差别,但这不影响本文得出结论:多芯激励多芯光纤的串扰可以等同于每个激励纤芯分别激励时的串扰之和。纤芯2、4、6 分别激励与单芯激励关系的原理如图9 所示。

图9 纤芯2、4、6 分别激励与单芯激励关系的原理
对于情况3,纤芯2~7 为激励纤芯,纤芯1 为耦合纤芯。当外部纤芯同时激励时,纤芯1 的耦合功率如式(20)所示,其串扰如式(25)所示。当外部纤芯分别进行激励时,由于其激励纤芯的对称性,各个外部纤芯对纤芯1 耦合的功率相等,即P1,2(z)=P1,3(z)=P1,4(z)=P1,5(z)=P1,6(z)=P1,7(z),并且其表达式如式(26)所示,并且其串扰也相等,如式(29)所示。本文在纤芯2~7 分别激励和同时激励情况下,仿真了其归一化功率和芯间串扰与传输距离的关系,如图10 所示。图10(a)中,P1-n(z),n= 2,3,…,7表示纤芯2~7 分别激励时对纤芯1 耦合的功率,由于外部纤芯在七芯光纤模型中处于外部位置,呈中心对称分布,其对纤芯1 耦合的功率都相等。P1-sum(z)表示纤芯2~7 分别激励时对纤芯1耦合的功率之和,且P1-sum(z)= 6P1-n(z),n= 2,3,…,7。P1-234567(z)表示纤芯2~7 同时激励时对纤芯1 耦合的功率。从图10(a)中可以看出,纤芯2~7 分别激励时对纤芯1耦合的功率之和与纤芯2~7同时激励时对纤芯1 耦合的功率相等,即P1-sum(z)=P1-234567(z)。图10(b)中,XT1-n,n= 2,3,…,7表示纤芯2~7 分别激励时对纤芯1 的串扰且都相等。XT1-sum表示纤芯2~7 分别激励时对纤芯1 耦合的串扰之和,且 XT1-sum=6XT1-n,n= 2,3,…,7。XT1-234567表示纤芯2~7 同时激励时对纤芯1 耦合的串扰。从图10 中可以看出,纤芯2~7分别激励时对纤芯1耦合的串扰之和与纤芯2~7同时激励时对纤芯 1 耦合的串扰相等,即XT1-sum=XT1-234567,图10(b)中串扰结果略有偏差的原因是多芯激励和单芯激励下串扰计算方式略有不同。此处的结果也验证了上述得出的结论。纤芯2~7 分别激励与单芯激励关系的原理如图11 所示。

图10 纤芯2~7 分别激励和同时激励下归一化功率和芯间串扰与传输距离的关系
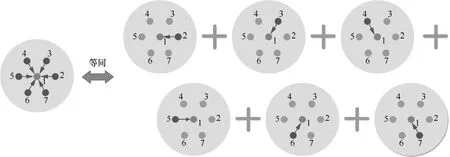
图11 纤芯2~7 分别激励与单芯激励关系的原理
文献[18]将七芯光纤的多芯激励的串扰等效成多个双芯光纤模型单芯激励情况的线性叠加,本节将七芯光纤的多芯激励串扰等同于七芯光纤中多个单芯激励的叠加,并且每个单芯激励的耦合都是通过直接求解七芯光纤的功率耦合方程得出的,这更符合实际多芯激励情况。通过以上对纤芯2、4、6 和纤芯2~7 同时激励和分别激励情况下对耦合纤芯的功率和串扰情况分析,本文可以得到如下结论:多芯激励下多耦合纤芯串扰的贡献是不相关的,多芯激励的串扰等同于每个激励纤芯分别激励得到的串扰之和。
3 结束语
本文考虑多芯激励下的七芯光纤,选取了3 种多芯激励模型,根据七芯光纤的功率耦合方程,推导了多芯激励下实际七芯光纤的功率和ICXT 的解析表达式,研究了多芯激励下归一化功率和串扰随距离的变化关系。结果表明,由于实际光纤铺设中存在弯曲和扭转的影响,经过长距离传输后,各纤芯的归一化功率都会收敛到一个定值,达到动态平衡状态,并且其收敛距离随着弯曲半径的增大呈指数级减小,逐渐趋于一个定值。此外,本文还研究了多芯激励和单芯激励的关系,在多芯同时激励和分别激励下推导其功率和串扰解析表达式,并在仿真分析中得出多芯激励本质特性,即多芯激励对串扰的贡献是不相关的,多芯激励多芯光纤的串扰可以等同于每个激励纤芯单独激励时的串扰之和。该结论适用于任意纤芯数量多芯光纤以及任意纤芯数量激励的情况,为多芯光纤传输系统的多通道传输信号的研究提供了理论基础。
