多基色显示系统基色亮度求解及讨论
2024-04-03姚昞晖邓林宵许立新
姚昞晖,邓林宵,许立新*
(1.中国科学技术大学 核探测与核电子学国家重点实验室,合肥 230026,中国;2.中国科学技术大学 物理学院 安徽省光电子科学与技术重点实验室,合肥 230026,中国;3.先进激光技术安徽省实验室,合肥 230026,中国)
0 引 言
从早期的黑白显示到现在蓬勃发展的激光显示[1],显示一直在人们的生活中扮演着重要的角色,人们对它的要求也越来越高。显示色彩的优劣直接影响显示的效果。对于显示系统,通常使用色域来衡量其显示颜色的能力[2]。色域越大,则显示系统可渲染的颜色越丰富。为了定量表征颜色,国际照明委员会(Commission Internationale de I’Eclairage,CIE)首先提出了CIEXYZ颜色空间,并将其简化为xy色度图[3],其直观的特点让其被广泛应用在显示领域来表征色域。但颜色是一个3维的物理量,2维的xy色品图为了直观而牺牲了亮度属性,这也导致其准确性相对较低[4]。为了更准确地描述人眼感知的颜色,CIE进一步提出了CIEL*a*b*颜色空间,它是目前应用最广泛的均匀颜色空间[5]。立体颜色空间中的色域称为立体色域。在均匀颜色空间中,精确定量描述颜色成为可能[6]。MAcADAM最早于1935年提出了计算色域的方法[7],但由于时代限制,只将色域在xy色品图中进行了表示[8]。MASAOKA改进了他的方法,并将其应用于立体颜色空间,获得了立体色域[9]。而WANG等人继续改进了MAcADAM的方法,使其适用于当前常见的基色显示系统[10]。WANG等人进一步研究了色温或者说白平衡点色坐标对色域的影响[11]。根据这些研究可以看出,目前的三基色显示系统的理论基础已经较为完备。在此基础上,为了方便不同设备之间色彩还原的准确性,美国国家电视标准委员会(National Television Standards Committee, NTSC)与电影和电视工程师协会等提出了NTSC Rec.709[12]、Rec.2020[13]等色域标准,其对应的色域大小也不尽相同,其中Rec.2020是当今最先进的色域标准。《中国制造2025》中明确提出,2020年激光显示的色域要达到160% NTSC标准所对应的色域,2025年要进一步达到200% NTSC标准所对应的色域,这说明色域有重要意义且具有很高的研究价值。
随着激光光源的发展,三基色激光显示系统已经达到149% NTSC的平面色域面积[14],这说明减小基色谱宽是提升色域的重要方法,但基色谱宽过窄会导致激光散斑增大的问题[15],并且三基色显示系统的上限较为明显[16]。为了进一步提升色域,势必要采用多基色显示的方案[17]。随着多基色显示技术的发展,目前已经有相关的研究,成功搭建了六基色显示系统,并使其立体色域的体积超过了180% NTSC[18]。在作者团队前期的研究中,提出了多基色显示系统基色亮度通解的计算方案,利用格拉斯曼定律来获得多基色显示系统对应的亮度解空间,以得到其所有可能的基色搭配,并采用实际的六基色显示系统进行了验证[19],但这些探究尚不完善。本文作者将对之前提出的解空间理论计算的数学形式进行规范化,并对其数学形式上的完备性和等价性进行证明。进一步地,将探究了解空间的几何性质,并采用理想的多基色显示系统进行演示。为简化起见,本文中的讨论仅限于颜色可加性良好的显示系统,为了探究显示系统的基本特性,本文中不考虑不同环境光源对颜色外观带来的颜色变化,即认为显示系统位于一个理想暗室中。
1 多基色显示系统的基色峰值亮度推导
对于显示系统而言,存在一个最基本的约束条件,即所有基色的最高亮度之和为白色,该白色也称为该系统的白平衡点。为了更好地说明多基色显示系统亮度通解的求解,此处对作者团队之前的工作进行了数学形式的优化。根据格拉斯曼定律,一个颜色可以由3种在颜色空间中不共线的颜色混合而得到,利用公式表达,即为:

(1)

(2)
式中:X,Y,Z及其下标1,2,3分别代表三基色的三刺激值;x,y,z代表对应的色坐标,下文同理;下标mix代表混合后的颜色。如果令混合后的颜色为白色,则最终得到的计算结果就是常见的三基色显示系统。在已知基色和白色的色坐标的前提下,上述6个方程可以简化成含有3个未知数的三方程组,因此对应特定的基色和白色,三基色显示系统只有一组特定的Y刺激值的解。需要说明的是,Y刺激值和亮度存在对应的转化关系,因此获得了Y刺激值即相当于获得了基色的亮度比例。而对于N(N>3)基色显示系统,令j=N-3,公式则变为:
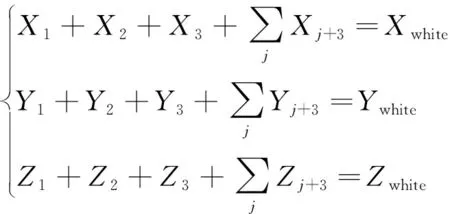
(3)
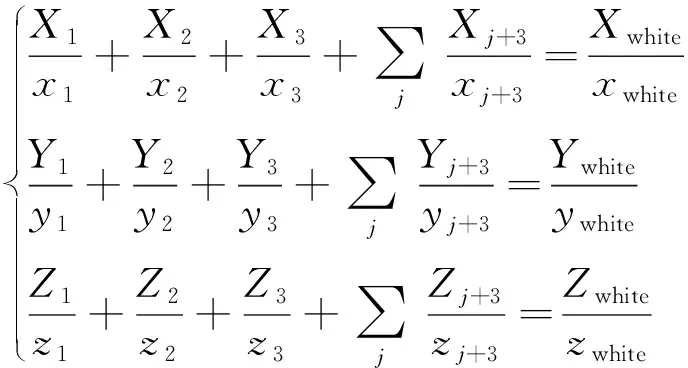
(4)
式中:下标white代表白色。显然,对于多基色系统,上述方程由于增加了新的未知数,因此变为不定解方程,不存在如同三基色系统的一组定解来获得白平衡,而是有无数种解。这对控制多基色显示系统的白平衡,以及优化系统的基色参数提出了挑战。
对于一个N(N>3)基色显示系统,假设已知所有基色的色坐标和白色的色坐标。首先任意选取其中3个基色,得到如下刺激值条件限制:

(5)
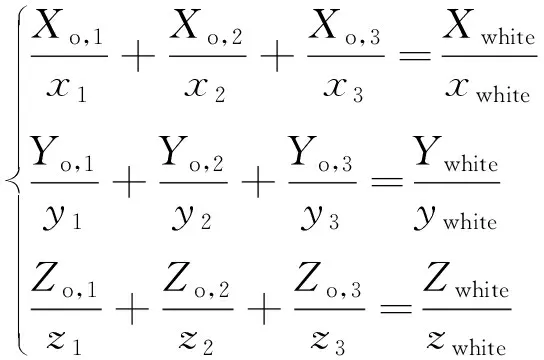
(6)
式中:下标o代表选取的初始三基色混合成白色的情形。计算得到Yo,1,Yo,2,Yo,3,该结果代表选取的初始三基色混合成白色所需要的Y刺激值。在理论计算中通常令Ywhite=100来简化计算,再将第j+3 (j≥1)个基色用前3个基色进行表示,有:
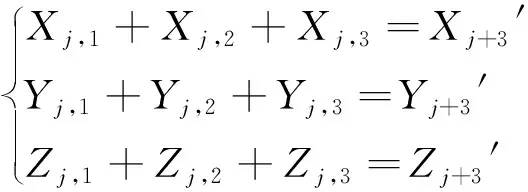
(7)

(8)
式中:下标j代表初始三基色混合成第j+3个基色的情形;Xj+3′,Yj+3′,Zj+3′代表此时第j+3个基色的三刺激值;xj+3,yj+3,zj+3代表其对应色坐标,下文同理。假设第j+3个基色的Y刺激值为kjYj+3′,引入kj参数作为变量,并令Yj+3′为常数方便计算,用这6个式子可以计算出Yj,1,Yj,2和Yj,3。由于多基色系统的定义是每个基色都不能由其它基色混合得到,因此此时Yj,1,Yj,2和Yj,3必然有负值,但并不影响后续计算,则此时多基色系统满足:
(Yj,1+Yj,2+Yj,3)]=Ywhite
(9)
即:
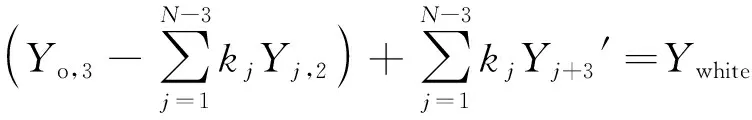
(10)
上述两个式子的物理意义是:为了增加新基色的Y刺激值,则必须按照比例降低原有三基色的Y刺激值;不难看出,式中每一项即对应每一个基色的Y刺激值。对于多基色显示系统,每个基色的Y刺激值都应该大于0,因此有:
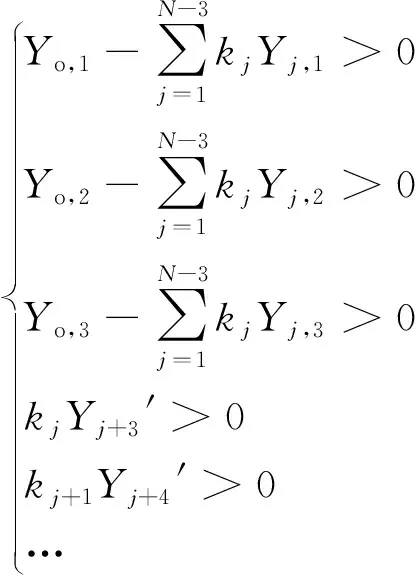
(11)
此不等式组即为N(N>3)基色系统的解空间,根据不等式组的性质,不难得出解空间的维度为N-3,而此时解空间中的点(k1,k2, …,kj, …)对应的多基色系统的基色亮度解为:
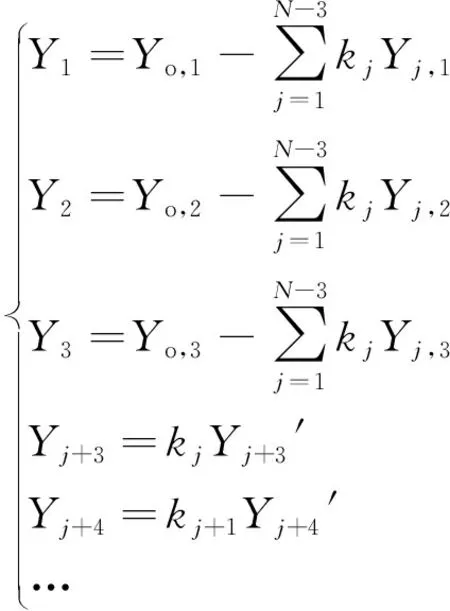
(12)
式中:Yj+3′都为常数,为了计算方便,通常设置为100。获得了每个基色的Y刺激值后,根据每个基色的色坐标(xi,yi)(其中i=1,2,…,N)求出所有基色的三刺激值,将显示系统的亮度按照Y刺激值的比例进行设置,即可得到一个多基色显示系统。
在获得了三刺激值后,在立体颜色空间中,根据参考文献[20]中的计算方法,即得到立体色域,代表此多基色显示系统可以显示颜色的集合,目前最常用的立体颜色空间为CIEL*a*b*颜色空间。对于一组特定的基色和白平衡点参数,比较解空间中不同点对应的立体色域,即可获得某组基色的最优亮度组合;而对比不同的基色和白平衡点参数组合的解空间,即可获得最优的基色组合。
2 对解空间完备性和等价性的讨论
首先,只有获得多基色显示系统的所有可能的参数组合前提下,才能进行最优化。因此有必要证明上述推导中的解空间是完备的,即该解空间包含了该特定基色和白色参数组合下所有的Y刺激值的可能搭配。
此处证明采用反证法。假设在某基色和白色参数组合下,存在一组Y刺激值(Y1′,Y2′,…,Yj′,…)在解空间中不存在点(k1,k2,…,kj,…)和其对应。将(Y1′,Y2′,…,Yj′,…)代入式(12),由于式(12)的未知数为Yo,1′,Yo,2′,Yo,3′和kj′,未知数数目和方程数一致,且方程互相线性无关,故该方程可必然反解出唯一解(k1′,k2′,…,kj′,…),此点不在解空间内,故该点必然不满足式(11),即Yj′中存在负值。因为Y刺激值和亮度可按照比例对应,由于负亮度不存在,故不存在这样一组Y刺激值不在式(11)和式(12)的包含范围内。因此解空间是完备的。
然后需要证明解空间的等价性。从之前的推导中可以看出,解空间的推导基于最先选择的三基色的参数。不同的初始三基色计算出来的解空间的范围显然不同。但是,解空间中的点对应的基色Y刺激值是等价的,即一个初始三基色计算出的解空间中的点(k1,k2,…,kj,…)对应的一组基色Y刺激值,必然可以在另一组初始三基色计算出的解空间找到一个对应点(k1*,k2*,…,kj*,…)。
对于解空间1,其中的坐标点(k1,k2,…,kj,…)对应的基色Y刺激值如下式所示:
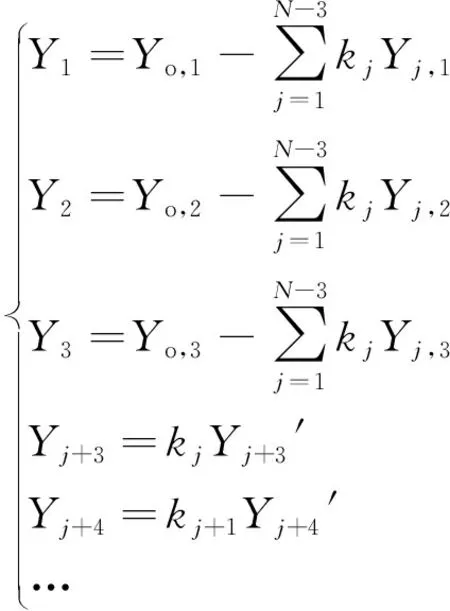
(13)
其对应的解空间为:
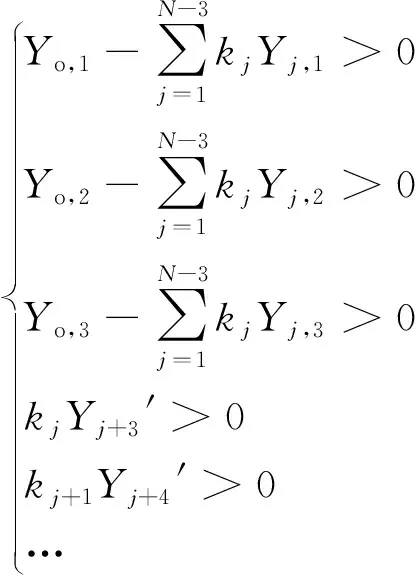
(14)
对于解空间2,初始三基色更换后,其解空间和基色Y刺激值如下所示:
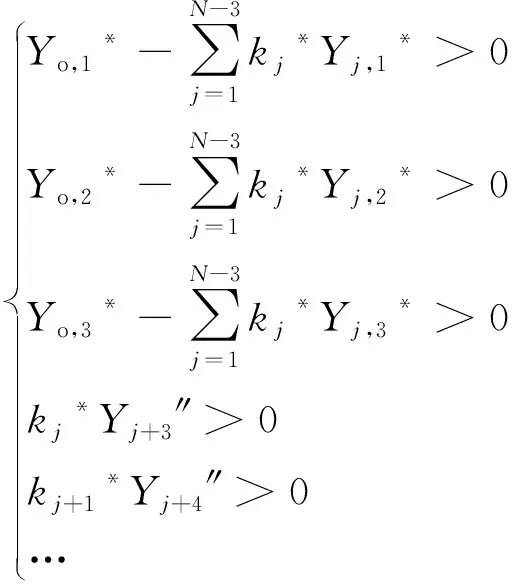
(15)
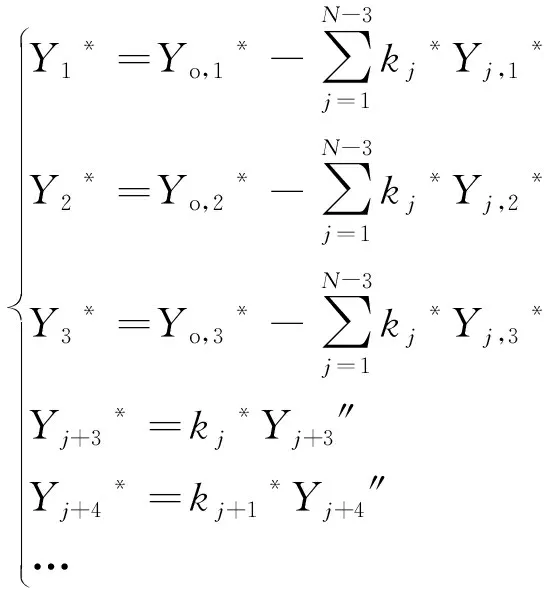
(16)
注意此时的两套符号中,虽然仍为原基色组,但编号顺序发生了变化,这是由于选取的初始三基色不同导致的,也即式(13)和式(14)中的Yi与式(15)及式(16)中的Yi*(其中i=1,2,…,N)代表不同的基色,相当于交换了顺序,更换了初始三基色,原先用来表征其它基色的颜色变成了被表征颜色,而Yj+3′和Yj+3对应,Yj+3″和Yj+3*对应,形式的含义和式(11)、式(12)表征的解空间的基本形式一致。根据解空间的完备性,即式(13)和式(15)对应的解空间都是完备的,则解空间1中的基色Y刺激值组,必然满足式(15),因此根据式(16)必然可以反解出解空间2中的唯一点(k1*,k2*,…,kj*,…)。因此不同初始三基色的选择虽然会导致解空间的差异,但是由解空间中的点导出的基色Y刺激值组,是完备并且一致的。由此可以得出结论:该方案对于多基色系统的基色亮度计算是成功的。
3 计算范例及解空间的相关性质
为了进一步说明本文中的算法,现采用模拟样例进行说明。表1中给出了模拟样例的色坐标,这里从三基色激光显示系统出发,添加新基色扩展为四基色、五基色和六基色系统,观察其解空间的演化。最初的三基色显示系统,选择其色坐标匹配Rec.2020色域标准。白色的色坐标(xwhite,ywhite)均设置为(0.3127,0.3290),其Y刺激值设置为100。表中3P,4P,5P,6P分别代表三基色、四基色、五基色、六基色激光显示系统,R1,R2,G1,G2,B1,B2分别代表不同波长的两种红基色、绿基色和蓝基色。

表1 模拟中采用的基色色坐标Table 1 Chromatic coordinates in the simulation
对于三基色系统,根据式(5)和式(6)可计算出:
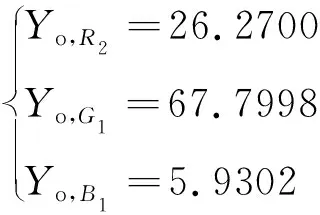
(17)
根据MASAOKA提出的方案[20]来计算立体色域,在CIEL*a*b*空间中画出其立体色域,如图1所示。图中,L*为亮度,a*轴正负分别代表红绿色,b*轴正负分别代表黄蓝色,其立体色域的体积为1854900。
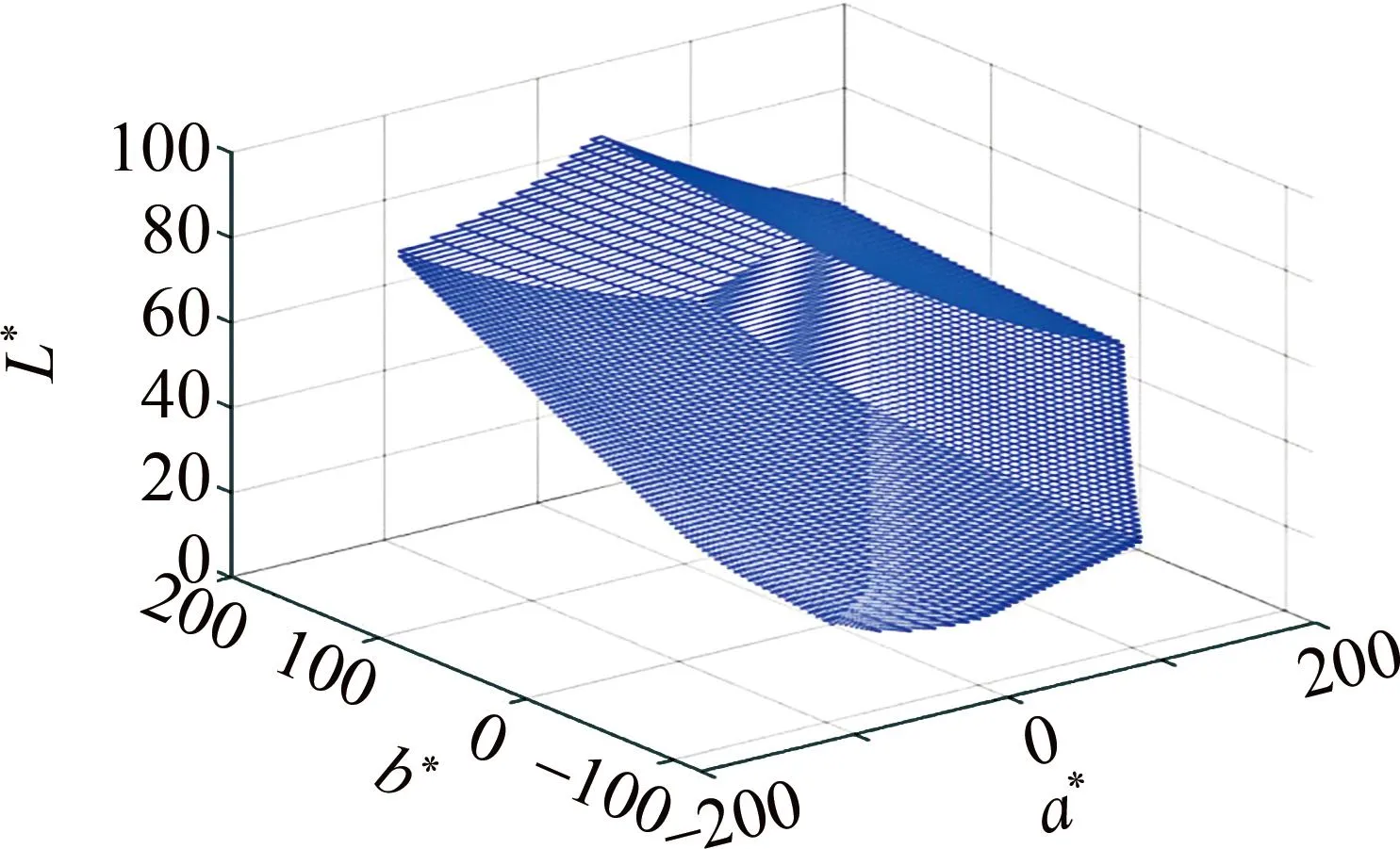
图1 R2,G1,B1构成的理想三基色显示系统的色域Fig.1 Gamut of the ideal three-primary color display composed of R2,G1,B1
利用式(1)和式(2),将第4个基色G2用初始的三基色R2,G1,B1进行表示,有:

(18)
代入式(11),得到四基色显示系统的解空间:
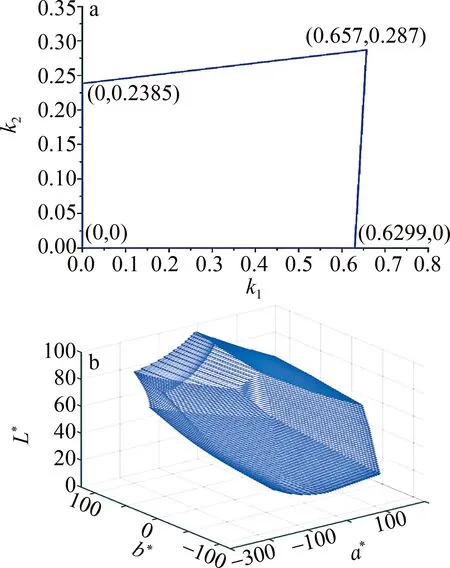
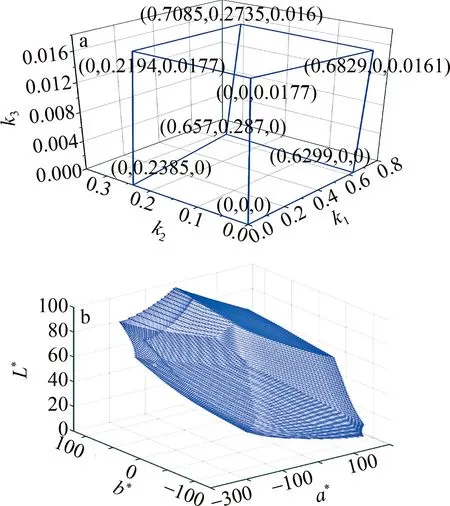
0 (19) 图2a中给出了四基色显示系统的色域体积随k1变化的趋势。利用MASAOKA提出的多基色立体色域计算方法[20]对色域体积进行计算,可以看出,在k1=0.34时,色域体积取最大值2185100,此时色域如图2b所示。 图2 a—解空间及对应的k1的取值范围和色域体积 b—当k1=0.34时的色域Fig.2 a—solution space and the range of k1 and the corresponding values of color gamut volume b—the gamut when k1= 0.34 再添加基色R1,同样按照上述步骤,有: (20) 图3a为五基色显示系统的解空间,在一个平面范围;图3b为k1=0.34和k2=0.15时的立体色域,色域体积为2258400。 图3 a— 解空间及对应的k1和k2的取值范围 b—当k1=0.34,k2=0.15时的色域Fig.3 a—solution space and the range of k1 and k2 b—the gamut when k1=0.34 and k2=0.15 对于六基色显示系统,添加基色B2,同样的,有: (21) 其解空间如图4所示。当k1=0.34、k2=0.15、k3=0.01时,立体色域如图4b所示,色域体积为2395800。 图4 a—解空间及对应的k1,k2和k3的取值范围 b—当k1=0.34,k2=0.15,k3=0.01时的色域Fig.4 a—solution space and the range of k1, k2 and k3 b—the gamut when k1=0.34, k2=0.15 and k3=0.01 根据图例中的解空间可以看出,每增加一个基色,解空间就增加一个维度。本文中的解空间获取,是在基色亮度无限制的情况下进行计算的。在实际应用中,考虑到实际光源的亮度和成本限制,必然存在更多的约束条件,比如要求某种基色的亮度低于某个值。在这种情况下,就需要对计算添加更多的约束条件,即增加不等式的数目,但这并不改变解空间的维度,只是改变了解空间的形状。在约束后的解空间中,依旧可以采取同样的方式,来获得需要的基色亮度配比。从上述的计算样例中可以发现,四基色显示系统的解空间,为五基色显示系统的解空间的一条边界,而五基色显示系统的解空间,为六基色显示系统解空间的底面。因为解空间由式(11)构成,其边界应当为其中某些不等式等于0的情形,即对应维数降低的显示系统。因此N基色显示系统的解空间的边界实际上涵盖了(N-1),(N-2)…,一直到三基色,所有以这些参数作为基色的理论显示系统的解空间。本文作者提出的方法成功解决了多基色显示系统中基色亮度选择的问题。结合色域体积的计算,可以对多基色显示系统的光源参数进行适当的优化,以满足实际的显示需求。 基于多基色显示系统和和三基色显示系统的差异,本文作者通过参数不等式的方式,在给定白平衡点和基色色坐标的情况下,理论上推导了多基色显示系统中基色亮度的设置问题。求解出多基色显示系统的亮度所对应的解空间,并对解空间的等价性和完备性进行了证明。同时,本文中采用理想的四基色、五基色和六基色显示系统对整体算法进行了演示,并探究了解空间的相关性质。结合立体色域的计算,通过遍历解空间,可以很容易地得到理论最大色域体积。该算法可以推广至任意种光源的多基色显示系统。结合色域体积的计算,该理论可用于指导基色波长、谱宽和亮度的选择。在未来的工作中,将继续探索基于该方法的颜色管理理论,提升色彩的还原程度和表现力。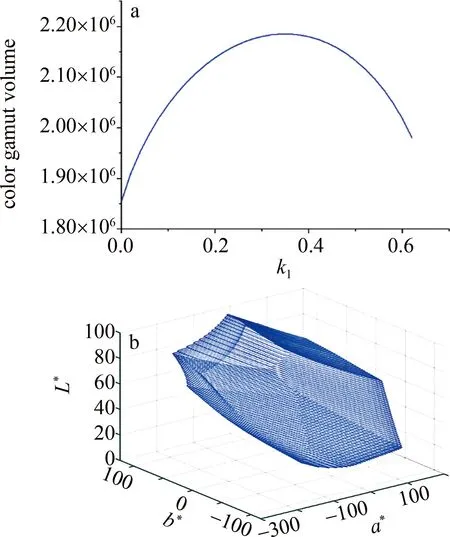
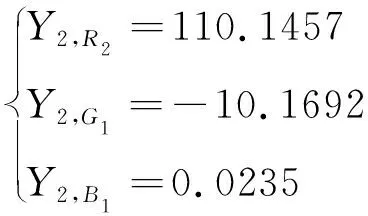
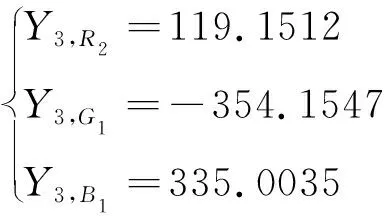
4 讨 论
5 结 论
