几何最值中巧用隐形圆解题
2024-03-31付波勇
付波勇
在初中数学题型中,有一类涉及到动点与最值的几何题型,题目中并没有圆,但是动点的运动轨迹形成了圆,从而转化为与圆有关的最值问题,我们把这种类型称为最值问题的隐形圆模型。这里对此进行探究,以找出它们共有的特征,总结出解题方法。
实际教学时,教师可先复习圆外一点到圆上的最长距离与最短距离的求解方法。
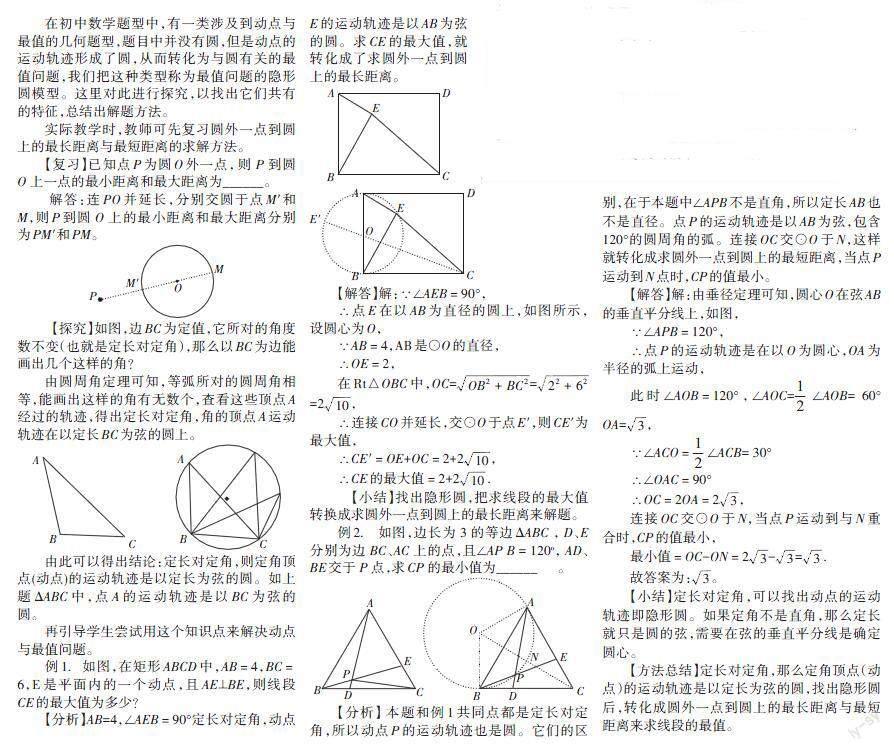
【复习】已知点P为圆O外一点, 则 P 到圆O 上一点的最小距离和最大距离为______。
解答:连PO并延长,分别交圆于点M′和M,则P到圆 O 上的最小距离和最大距离分别为PM′和PM。
【探究】如图,边BC为定值,它所对的角度数不变(也就是定长对定角),那么以BC为边能画出几个这样的角?
由圆周角定理可知,等弧所对的圆周角相等,能画出这样的角有无数个,查看这些顶点A经过的轨迹,得出定长对定角,角的顶点A运动轨迹在以定长BC为弦的圆上。
由此可以得出结论:定长对定角,则定角顶点(动点)的运动轨迹是以定长为弦的圆。如上题ΔABC中,点A的运动轨迹是以BC为弦的圆。
再引导学生尝试用这个知识点来解决动点与最值问题。
例1.如图,在矩形ABCD中,AB=4,BC=6,E是平面内的一个动点,且AE⊥BE,则线段CE的最大值为多少?
【分析】AB=4,∠AEB=90°定长对定角,动点E的运动轨迹是以AB为弦的圆。求CE的最大值,就转化成了求圆外一点到圆上的最长距离。
【解答】解:∵∠AEB=90°,
∴点E在以AB为直径的圆上,如图所示,设圆心为O,
∵AB=4,AB是⊙O的直径,
∴OE=2,
在Rt△OBC中,OC=[OB2+BC2]=[22+62]=2[10],
∴连接CO并延长,交⊙O于点E′,则CE′为最大值,
∴CE′=OE+OC=2+2[10],
∴CE的最大值=2+2[10].
【小结】找出隐形圆,把求线段的最大值转换成求圆外一点到圆上的最长距离来解题。
例2. 如图,边长为 3 的等边ΔABC , D、E 分别为边 BC、AC 上的點,且∠AP B = 120?, AD、BE交于 P 点,求CP 的最小值为______ 。
【分析】 本题和例1共同点都是定长对定角,所以动点P的运动轨迹也是圆。它们的区别,在于本题中∠APB不是直角,所以定长AB也不是直径。点P的运动轨迹是以AB为弦,包含120°的圆周角的弧。连接OC交⊙O于N,这样就转化成求圆外一点到圆上的最短距离,当点P运动到N点时,CP的值最小。
【解答】解:由垂径定理可知,圆心O在弦AB的垂直平分线上,如图,
∵∠APB=120°,
∴点P的运动轨迹是在以O为圆心,OA为半径的弧上运动,
此时∠AOB=120°,∠AOC=[12] ∠AOB= 60° OA=[3],
∵∠ACO=[12] ∠ACB= 30°
∴∠OAC=90°
∴OC=2OA=2[3],
连接OC交⊙O于N,当点P运动到与N重合时,CP的值最小,
最小值=OC-ON=2[3]-[3]=[3].
故答案为:[3]。
【小结】定长对定角,可以找出动点的运动轨迹即隐形圆。如果定角不是直角,那么定长就只是圆的弦,需要在弦的垂直平分线是确定圆心。
【方法总结】定长对定角,那么定角顶点(动点)的运动轨迹是以定长为弦的圆,找出隐形圆后,转化成圆外一点到圆上的最长距离与最短距离来求线段的最值。
