成人计算整数除法的试商策略探查

巩子坤 余丽丽

【摘   要】试商是整数除法的重点和难点。当前教材对试商策略的编排较为繁琐，未能关注到通性通法，导致学生频繁出现试商错误，而成人在计算整数除法时，总能表现得游刃有余。为探究易于学生掌握且长久有效的试商策略，研究调查了成人计算不同类型的整数除法时采用的试商策略，并与教材编排的试商策略进行比较。结果发现：成人在采用教材中的四条试商策略之余，还生成了教材之外的“五舍试商法”与“直接试商法”；无论“五入”试商是否需要调商，成人均主要采用“五舍試商法”；“四舍”或“五入”试商均需调商时，部分成人一贯采用“直接试商法”。最后，对教材编写与教师教学提出建议。

【关键词】成人；整数除法；试商；策略

一、研究缘起

《义务教育数学课程标准（2022年版）》提出了在运算教学中要注重运算能力的培养。加、减、乘、除运算是小学数学“数与运算”中最重要的知识与技能，其中，除法虽然是四则运算中最后学习的运算，但从学习的逻辑顺序和内容比重上看，它的重要性和难度都不容小觑［1］。现行不同版本教材都以螺旋上升的方式编排有关整数除法的内容，而“除数是两位数的除法”单元是小学阶段整数除法最后安排的教学内容，在此单元中解决整数除法的算法问题，可以促进算法的迁移［2］。除此之外，相较于其他整数除法内容，“除数是两位数的除法”无法直接利用口诀试商，且需要多次调商，计算过程复杂，学生容易出现算法错误。

因此，研究“除数是两位数的除法”的算法问题具有典型性，其中试商更是学生运算过程中的“重灾区”。学生在计算除数是两位数的除法时，存在试商速度较慢、试商的除数选择不恰当等问题，使得计算结果容易出现偏差［3］14。原因可能是教材在“除数是两位数的除法”单元中，过于强调用“四舍五入法”进行试商［4］，且针对不同类型的算式还呈现了“凑五试商法”“同头无除试商8、9”“除数折半估商5”等多种试商策略，使得认知水平较低的学生掌握的试商策略过于繁杂，无法形成试商技能［5］，最终导致学生在计算整数除法时困难重重。

与之相反，成人在计算整数除法时往往游刃有余。作为整数除法的关键运算技能，试商是否被成人完全掌握？成人是否会生成教材之外的试商策略？本研究通过问卷调查，梳理成人计算除数是两位数和除数是三位数的除法时的试商策略，并与教材呈现的试商策略进行比较，进而为教材编写与教师教学提出建议。

二、研究设计

（一）研究对象

本研究的调查对象为浙江省某师范大学数学与应用数学专业的在校大学生，也就是本文所说的成人。其中，男生26人，女生37人。

（二）研究方法

1. 问卷法

为探查成人计算整数除法的试商策略，设计了四道计算题。发放问卷63份，回收有效问卷63份。

2. 访谈法

为深入了解成人的试商策略，问卷测试完成之后，挑选若干名被试，针对问卷内容进行一对一访谈，并用录音笔记录访谈内容。

（三）问卷设计

问卷共有四个问题，均为整数除法计算题，但类型有所不同，包括“四舍、无调商”“四舍、需调商”“五入、无调商”和“五入、需调商”四种类型，具体内容如下。

考虑到成人心算的能力已经十分成熟，试商的过程可能隐含在成人心算的过程中。因此，要求被试在问卷中不仅要保留笔算过程，还要借助文字或横式表达出计算的全过程，从而完整地展示被试的试商策略。例如在计算7942÷47时，可以分两步来表达心算过程：第一步，每一次试商时，脑海里最先想到商几，是如何想到这个数的？第二步，想到商几后，通过什么方法验证试商的结果是合适的？

（四）数据处理

问卷回收后，对问卷内容进行赋分［6］：计算结果错误，记0分；计算结果正确，记1分。此外，由两名评分者对被试计算整数除法的试商策略分别编码（具体策略见下文），结果显示编码的一致性信度为0.943，说明编码的信度较高，并针对不一致的编码结果进行讨论，形成一致意见。

三、研究结果与分析

（一）成人计算整数除法的试商策略

1.策略类型

通过对问卷进行统计分析，发现被试主要采取以下五种策略进行试商。

策略一：“四舍试商法”。当除数的个位介于0～4之间时，通过“四舍”将除数看成与它接近的整十数，利用乘法口诀试除被除数［3］15。例如，在计算238÷32时，使用“四舍试商法”，无需调商。由于除数是两位数，故与被除数前两位进行比较，23＜32，则商在个位且被除数向后多看一位；将32“四舍”为30，计算238÷30，联想3的乘法口诀，几×3（十）最接近且小于238，得到个位试商7（如图1）。

策略二：“五入试商法”。当除数的个位介于5～9之间时，通过“五入”将除数看成与它接近的整十数，利用乘法口诀试除被除数［3］15。例如，在计算7942÷47时，使用“五入试商法”，无需调商。由于除数是两位数，故与7942的前两位进行比较，79>47，则商在百位；将47“五入”为50，计算79÷50，联想5的乘法口诀，几×5（十）最接近且小于等于79，得到百位试商1。同理，由于余数32<47，故商在十位且被除数向后多看一位，仍将47“五入”为50，计算324÷50，联想5的乘法口诀，几×5（十）最接近且小于等于324，得到十位试商6。以此类推，得到个位试商8（如图2）。

策略三：“五舍试商法”。当除数的个位介于5～9之间时，将除数“五舍”为整十数后，再利用乘法口诀试除被除数。例如，在计算7942÷47时，使用“五舍试商法”，需要调商。由于除数是两位数，故与7942的前两位进行比较，79>47，则商在百位；将47“五舍”为40，计算79÷40，联想4的乘法口诀，几×4（十）最接近且小于等于79，得到百位试商1。同理，由于余数32<47，故商在十位且被除数向后多看一位，仍将47“五舍”为40，计算324÷40，联想4的乘法口诀，几×4（十）最接近且小于等于324，得到十位试商8。以此类推，再在个位试商9（如图3）。

策略四：“凑五试商法”。当除数的个位为4、5、6时，将除数看作□5（几十五），通过口算找到几×□5最接近被除数，进行试商。例如，在计算682÷24时，使用“凑五试商法”，无需调商。由于除数是两位数，故与682的前两位进行比较，68>25，则商在十位；将24“凑五”成25，计算68÷25，易得3×25>68>2×25，所以十位试商2。同理，由于余数20<24，故商在个位且被除数向后多看一位，仍将24“凑五”成25，计算202÷25，易得25×4=100，所以个位试商8（如图4）。

策略五：“直接试商法”。直接利用做除法想乘法，口算（ ）×除数最接近被除数，跳跃加商进而调商［7］。例如，在计算7942÷47时，使用“直接试商法”，需要调商。由于除数是两位数，故与7942的前两位进行比较，79>47，则商在百位，且47×2>79>47×1，因此在百位上商1；又由于余数32<47，故商在十位且被除数向后多看一位，计算324÷47，口算几×47最接近324，易知1×47和2×47远小于324，故跳着试商，发现5×47和6×47依然小于324，但7×47>324，所以十位商6；最后，由于余数42<47，故被除数再向后多看一位，计算422÷47，口算10×47接近但大于422，所以尝试商9和8，发现9×47>422，8×47<422，因此在个位商8（如图5）。

此外，在成人计算过程中，极少部分出现了“除数折半估商5”和“同头无除试商8、9”的试商策略，但这是成人在特殊情形下所采用的试商策略，不属于本研究调查的四种除法类型下成人所采用的试商策略，故下文不作统计。

2.策略统计

通过统计，得到不同试商策略在不同类型除法算式中的使用率及正确率，如表1所示。

从表1中可以发现：

（1）当除法算式满足“四舍、无调商”时，95.24%的被试采用“四舍试商法”试商，且正确率达到98.33%；还有4.76%的被试选择“直接试商法”，且正确率达到100.00%。

（2）满足“四舍、需调商”时，有58.73%的被试仍采用“四舍试商法”试商，且正确率达到94.59％；有12.70%的被试选择“凑五试商法”，且正确率达到100.00%；还有28.57%的被试选择“直接试商法”，且正确率达到94.44%。

（3）满足“五入、无调商”时，有17.46%的被试选择“五入试商法”试商，且正确率达到90.91%；有20.64%的被试选择“直接试商法”，且正确率达到92.31%；还有61.90%的被试选择“五舍试商法”，且正确率达到94.87%。

（4）满足“五入、需调商”时，8.57%的被试仍选择“五入试商法”试商，且正确率达到100.00%；还有2.86%的被试选择“凑五试商法”，且正确率达到100.00%；然而有34.29%的被试选择“直接试商法”，且正确率达到91.67%；甚至有54.28%的被试选择“五舍试商法”，且正确率达到94.74%。

综上所述，成人在计算不同类型的整数除法时主要选择“四舍试商法”或“五舍试商法”，即把除数看作与它最高位的数字所对应的整十或整百数进行试商，并且正确率较高。

（二）教材中关于整数除法计算的试商策略

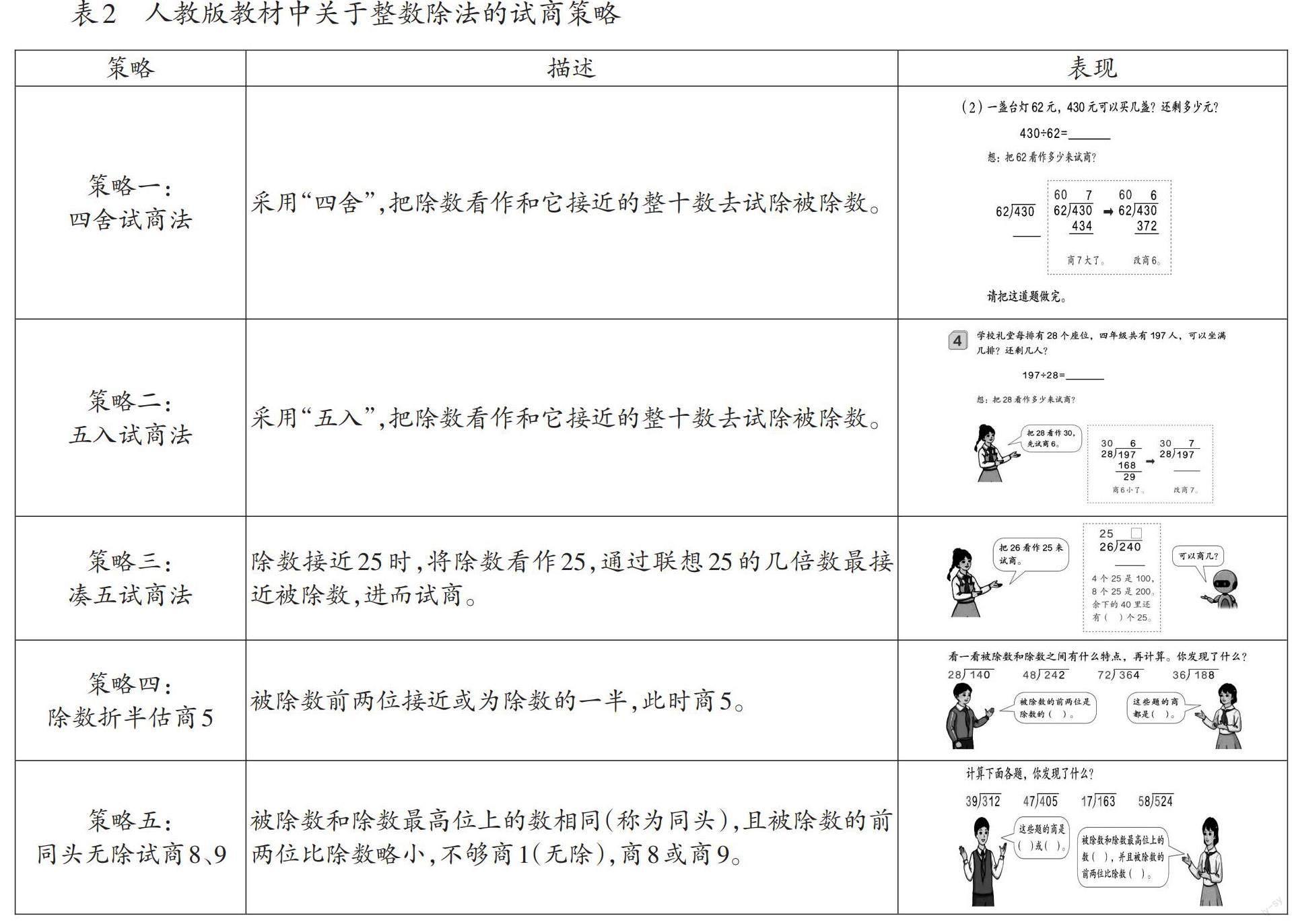
通过梳理人教版教材中“除数是两位数的除法”单元中的例题与课后习题，得到教材中关于整数除法的试商策略，如表2所示。

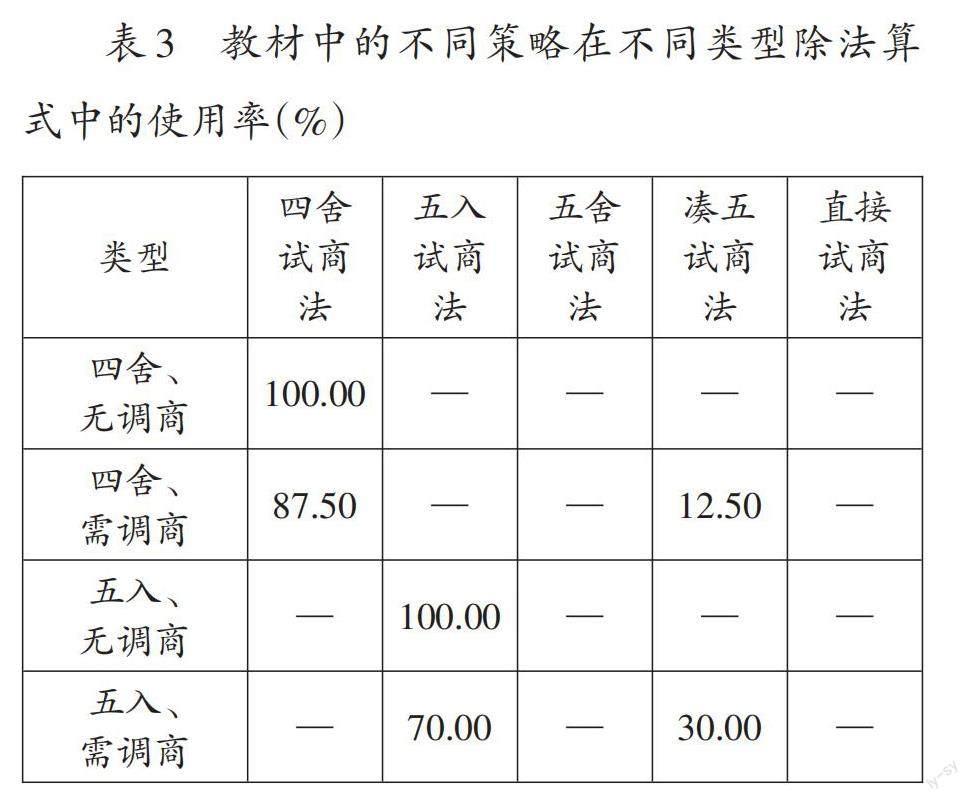
同样，通过统计教材中对于不同类型的除数是两位数的除法所采用的策略，得到不同策略在不同类型除法算式中的使用率，如表3所示。

（三）成人与教材的试商策略比较分析

1. 一致性

（1）除法算式满足“四舍、无调商”时，成人的计算策略与教材的策略均为“四舍试商法”

通过上述调查统计发现，对于满足“四舍、无调商”的除法算式，教材采用“四舍试商法”，即把除数看作和它接近的整十数去试除被除数。在此类除法中，95.24%的被试采用的策略与教材策略一致。

（2）除法算式满足“四舍、需调商”时，成人的主要计算策略与教材的主要策略均为“四舍试商法”

对于满足“四舍、需调商”的除法算式，教材主要采用“四舍试商法”，仅在少部分习题中选择“凑五试商法”。在此类除法中，有58.73%的被试采用“四舍试商法”，12.70%的被试采用“凑五试商法”。因此，超七成的被试采用的策略与教材策略一致。

2. 差异性

（1）除法算式满足“五入、无调商”时，教材使用“五入试商法”，成人主要采用“五舍试商法”

对于满足“五入、无调商”的除法算式，教材仅介绍“五入试商法”。在调查中，仅有17.46%的被试采用与教材一致的试商策略。另有61.90%的被试选择“五舍试商法”、20.64%的被试选择“直接试商法”试商，这与教材中的策略产生了差异。通过访谈得知，成人认为，“五舍试商法”将除数“五舍”后，保持除数的最高位不变，可以直接观察最高位快速试商，无需人为赋予一个新的除数，尽管调商次数可能会增加，但只需重复调小余数直至小于除数即可；“直接试商法”可以直接通过口算乘法试商并通过跳跃加或减商进行调整，直至余数小于除数。两种策略的产生均源于成人追求直观且熟练口算乘法。

（2）除法算式满足“五入、需调商”时，教材主要使用“五入试商法”，成人主要采用“五舍试商法”以及“直接试商法”

对于满足“五入、需调商”的除法算式，教材主要采用“五入试商法”，仅在少部分习题中使用“凑五试商法”。在调查中，仅有11.43%的被试采用的策略与教材策略一致。另有54.28%的被試采用“五舍试商法”试商，34.29%的被试采用“直接试商法”试商，这与教材中的策略产生了差异。这同样也是因为成人对直观的追求以及对口算乘法的熟练掌握。此外，只有当除数为25或26时，成人才会考虑使用“凑五试商法”，一方面是因为25易于构建整百数，另一方面是由于成人经过长期的练习，对25的几倍数已形成长时记忆，可直接将25的几倍数与被除数进行比较，提高了试商效率。

四、研究结论与建议

（一）结论

1. 成人仍继续使用教材中的四种试商策略，并生成了“五舍试商法”与“直接试商法”

成人在整数除法的运算过程中依然继续使用教材中的“四舍试商法”“五入试商法”“凑五试商法”“同头无除试商8、9”四种试商策略，但也使用了教材之外的“五舍试商法”与“直接试商法”。但是，针对不同类型的整数除法，成人采用的主要试商策略与教材并不完全一致，并且成人已不常用“五入试商法”与“凑五试商法”。

2. 无论“五入”试商是否需要调商，成人均主要采用“五舍试商法”

在各种类型的整数除法中，成人主要考虑使用“舍”的策略进行试商。其中，在计算“四舍、无调商”和“四舍、需调商”类型的除法算式时，成人与教材采用的策略一致，均主要采用“四舍试商法”。然而，在计算“五入、无调商”和“五入、需调商”类型的除法算式时，为了提高试商的效率，成人使用的策略不同于教材，主要采用“五舍试商法”。

3. “四舍”或“五入”试商均需调商时，部分成人一贯采用“直接试商法”

在各种类型的整数除法中，均有成人使用“直接试商法”试商。其中，在计算“四舍、需调商”和“五舍、需调商”类型的除法算式时，更多的成人采用“直接试商法”试商。这恰恰说明大部分成人在计算复杂的除法时，会抛弃生硬的技巧，回归最直接的乘除法的关系进行找商。

（二）建议

1. 适当补充“五舍试商法”，帮助学生养成灵活试商的意识

众所周知，教材只是一个教学工具，教师应该“用教材”，而不是“教教材”。在“除数是两位数的除法”单元中补充“五舍试商法”内容作为思考环节，有助于教师引导学生比较“五入试商法”和“五舍试商法”二者的优缺点，感受“五舍试商法”与“五入试商法”并无本质区别，仅在找商的效率上有所不同，进而帮助学生选择试商策略，养成灵活试商的意识。

2. 贯彻“直接试商法”，促进学生掌握除法运算的通性通法

运算过程中对通性通法的追求可以使个体的思维更加灵活，运算更加优化［8］。“直接试商法”作为个体除法运算的自然状态，应该是除法运算的通性通法，能够带领学生经历试错和比较的过程，从而解决除法运算问题。因此，教材在“表内除法”“有余数的除法”“除数是一位数的除法”以及“除数是两位数的除法”单元应贯彻 “直接试商法”的策略。

3. 重视口算乘法的训练教学，提升学生的运算能力

成人之所以偏向于使用“五舍试商法”和“直接试商法”进行试商，是因为他们具有很好的口算能力。口算是学生计算的基本能力，教师在教学整数除法的过程中仍需重视学生口算乘法的训练，以推动学生运算能力的逐步提升。在学生熟练掌握基本试商方法之余，教师可以适当传授“同头无除试商8、9”“凑五试商”“除数折半估商5”等策略，在有效提升他们运算能力的同时，培养他们的数感，提升他们数学学习的兴趣。

参考文献：

［1］刘东伟. 小学整数除法的教学研究［D］.武汉：华中师范大学，2014.

［2］徐国裕.有效课堂从研读教材起步［J］.教育评论，2014（2）：123-125.

［3］曹永泉.除数是两位数除法试商方法的教学探究［J］.中小学数学（小学版），2013（7/8）：14-16.

［4］何伟，董连春，法旭，等.南疆小学生数学运算错误类型及分析：基于新疆大规模测评数据［J］.数学教育学报，2020，29（1）：70-75，80.

［5］刘方帅.化繁为简，以“借”代“理”：解决除数是两位数除法试商难的问题［J］.数学教学通讯，2021（28）：57-58.

［6］巩子坤，王敏，程玲，等.直观表征与形式表征，孰难孰易：师生选择的分数除法算理表征方式比较研究［J］.中小学教师培训，2020（1）：45-50.

［7］杨岚，王亚宁.浅谈珠心算除法的八种试商方法［J］.珠算與珠心算，2020（2）：38-42.

［8］吕世虎，吴振英.数学核心素养的内涵及其体系构建［J］.课程·教材·教法，2017，37（9）：12-17.

（1.杭州师范大学经亨颐教育学院 2.杭州师范大学中国教育现代化研究院）