深度调研 有效迁移 细化与比较
——以“商中间有0 小数除法”为例
2024-03-28甘肃省陇南市文县东坝中学小学部梁学勤
甘肃省陇南市文县东坝中学小学部 梁学勤
小学生数学学习中有两类问题需要注意,一是由于旧知巩固不扎实出现的老问题, 称之为“老病根”; 二是经验迁移不得力出现的新问题,这些可统称为“并发症”。 两类问题互有联系,并且在学生的练习中反复出现。“老病根”根除不了,“并发症”就会连续出现。 深刻调查学生出错的原因并对症下药很有必要,教师要准确把握学生的学情,预判可能出现的思维障碍,抓住学困点,辨清出错类型,并探究出针对性强的方法、策略和路径,提高学生的数学学习力[1]。
一、问题和困惑
人教版小学数学四年级下册的小数除法中涉及到商中间有0 的问题。 与商末尾有0 的问题相比,学生更容易在商中间有0 的计算中出错,有的弄不清算理,有的糊涂于算法,有的是整数除法中遗留下来的问题。 还有的学生因为多了个小数点,碰到“商中间有0 小数除法”就头疼,过往的经验无法有效迁移, 数位上稍不注意就会出错,就会引发新问题。
二、调查与分析
没有调查,就没有发言权。整体解决“老病根”与“并发症”,必须建立在学生真实学情的前测上,以便后续对策有依据,有针对性。我们选择四年一班与四年二班共90 名学生进行前测。商中间有0 整数除法的正确率远远大于商中间有0 的小数除法(见表1)。

表1 商中间有0 的整数除法与小数除法前测表统计
那么,出现如此明显差异的现象根源是什么呢? 是学生粗心大意,还是算理与算法的迁移不够呢? 为此我们进一步深入到一些细节之中进行调研,抽取了部分学生的竖式计算草稿,发现商中间漏0 的学生比比皆是。
探究学生如此竖式计算背后的原因很有必要。 于是,我们从问卷测试过渡到深入访谈,从更细微的层面梳理学生出错的原因。 访谈分三步走(见表2)。

表2 “商中间有0 小数除法”访谈一览表
访谈中得知, 优等生的想法中最重要的一个概念是“除法平均分”。他们做过太多“把算式按商的位数分一分”的试题。 这样的试题实际上就是强调商是几位数的问题,即商是几位数是有规律可循的,不能因为小数点的介入而少一位或者多一位。相比较而言,学困生的想法是错误的。显然,“够了才能分”不是除法(包括整数除法与小数除法)的本质属性。事实上,除法的本质是平均分,每次把余数的计数单位变小合并到下一个数位继续分,“商中为什么会有0” 是与平均分有关系的。 对于那些本身对除法核心概念理解不透彻的学困生而言,“老病根”自然会延续到“并发症”中。“够了才能分”这种观念导致的就是“被除数一定要大于除数”。 这样的惯性思维“害人不浅”——学生碰到“被除数比除数小”时就觉得茫然无措,很容易做出错误的判断或计算。
我们还访谈了那些喜欢估算的学生。商中间有0 的整数除法与小数除法,之所以前者正确率高,是因为整数除法中学生将估算运用得特别熟稔,但在小数除法中,估算不顶用了,稍不小心就会出错。比如面对2568÷24,估算能力较强的学生一眼可以看出最高位在百位,如果学生忘记了中间补0,那么17 这样的结果与估算相差太大,学生肯定会回头检查, 最终通过补0 形成正确答案。 但是面对16.2÷15 这道题, 理所应当添加0 也罢, 粗心大意漏掉0也罢,不影响估算的结果,由此出现大面积的错题成为常态。 可见,小数点的出现,对学生的惯性思维形成冲击,增加了运算的复杂性,引发了新问题,“老病根”与“并发症”同时存在。
在分析学情的基础上,我们进一步分析教材。 教材的编排蕴涵着极强的结构性和逻辑性,它由一个个知识点按照一定的知识序列排列组成[2]。但是教材毕竟是静态的,而且因为篇幅限制,诸多逻辑空白并未呈现出来,而这需要教师去发掘并填补。 如果教师疏于这方面的探究,也有可能会给学生造成误解及负面影响。
比如,下图中的内容就需要教师左右勾连,进行细微意义上的甄别及引领。 很多学生看到12.6÷12 的竖式后,误以为第二步中的60 是一次性移下来的,这也是“不够就移”思维定势的体现。如果教师不用心强调,不通过更多的练习进行举一反三或者举三反一,那么学生就会把这种误解迁移到其他试题的计算之中,由此错题的出现也就不足为怪了。
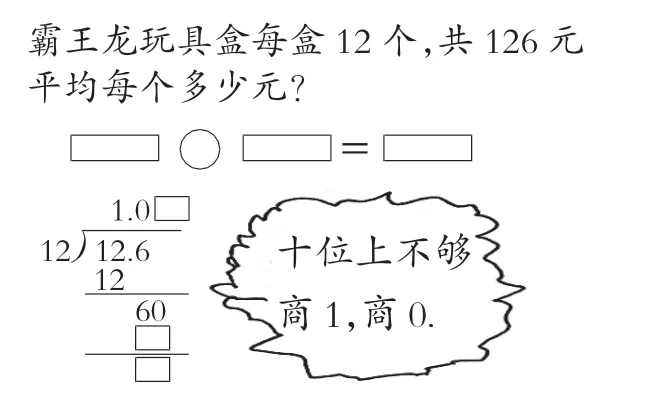
三、策略与思考
既然造成错误的根源是多方面的,那么,重新审视学生与教材以及重构教学的新框架就是大有必要的; 既然“老病根”是因为整数除法学得不扎实所导致,那么以跨单元与整体教学的姿态回到过去重温旧知,进行有意义的迁移、细化与比较,剔除学生思维中僵化与定势因子,就更是必要的。
(一)迁移:算理、算法一脉相承
所谓“迁移”,即在新旧知识联接点对学生加以点拨,即培养学生的知识迁移能力[3]。 学生迁移力的提升不是一蹴而就的,需要由此及彼的追问、换位思考的逆问,需要前后贯通、勾连,进行更深处的沿径探源。真正高质量的迁移必须是“有根”的,即把已有的方法、经验运用到未知的学习中,正所谓:“由根生干,由干生枝。 ”
就除法的本质属性而言,所谓的平均分,就是竖式中分到哪一位,商就写在哪一位上面,哪一位不够商1,就在那位上商0。 这一点,无论是整数除法还是小数除法,都是不变的,这样的算理、算法是一脉相承的。 所以,如果学生对此理解不透彻,教师就应该通过复习旧知,通过一些试题的训练再次强化除法的意义。
教师出示两道整数除法算式:①912÷3,②1260÷2,组织学生自主完成计算, 并说说商中间的0 是怎么来的。优等生可能会很快回答出来,但学困生则知其然而不知所以然。 因此,教师直接出示以下竖式图帮助学生理解之所以写0 的原因。

上图既有较为细致的过程,又有简化后的过程,简洁明了。通过对比,学生厘清了其算理与算法,明白了商中间0 的来历。这为学生学习小数除法起到承上作用。接下来,出示算式12.6÷12,从整数除法过渡到小数除法,形成承上启下——学生自然而然地迁移运用整除除法的方法去解决小数除法问题。 这里迁移发挥的是正迁移作用,而非负迁移,因为学生做到了两者之间算理、算法上的一脉相承。
但仅仅这样是不够的。 完成12.6÷12 一题后,教师进一步追问:“假如把小数点继续往左移一位, 结果会如何呢? ”请仔细观察下图中的三个竖式。

通过更为细微的对比,大部分学生已经发现了三个算式的相同之处,那就是不论什么“位”上的0,哪怕计数单位不同,但其产生的过程和方法是永远不变的——凡是某个数位上的数不够商时就补0。 这是除法的本质意义, 是解决任何题型都绕不开的。 这样的举一反三,促使学生完成了有意义的迁移,其效果事半功倍。
(二)细化:改变“不够就移”的做法
1.细化板书,消除负面影响
上文中那个学生误以为第二步中的60 是一次性移下来的。教材竖式过于简单,对于学困生而言,会造成理解障碍。 为此,我们“由粗到细”,进一步细化板书,将原来简单的一个竖式变为能够充分显示其细微过程的三个竖式。可以利用大屏幕动态演示其细微的过程。

教师引领学生用醒目的颜色划出其中关键的步骤及重点, 尤其表示出哪个数移下来了, 厘清哪个地方是商0还是移0。 当学生理解到这两点后,对所谓的“先商0 而后移0”的理解就显得水到渠成。
2.细化过程,破除思维定势
数学学习中的思维定势既有好处,又有坏处。 尤其是学生对数学核心概念理解不透的情况下, 其负面作用更大。“不够就移”这样的思维定势就是这样,就是造成学生漏0 现象的原因。因此,想方设法破除定势,帮助学生形成理性与科学思维, 应该成为解决小数除法中“老病根”与“并发症”的一个重点。 我们的做法是细化教学环节,引领学生针对最后一个竖式对如下三个问题进行充分讨论,最终达成共识。
一是“商中0 来自何方又去向何处”的讨论。教师鼓励学生自由表达,在此基础上,剔除不成熟的说法。以下是两种比较理想的说法:
生1: 我认为商中0 是这样来的:6 移下来是为了细分,分成6 个0.1,而这是不够分成12 份的。 既然不够分,那么其分的结果就应该为0。
生2:关于0 将去向何处,我是这么理解的:既然6 个0.1 平均分成12 份最后的结果是0 个0.1, 按照0 乘以任何数都是0 的法则,我们只能理解为没分走,所以这里的0可以省略。
二是“竖式中的60 可以一起移下来吗”的讨论。 针对“可以移下来”与“不能移下来”,教师组织两方学生进行辩论。 一种意见认为既然结果是不变的,那么完全可以移下来;另一种意见认为不能一起移下来,应该先移6,接着移0。其理由是十分位与百分位不同,直接移动的结果会造成中间的0 没有补上,少了平均分0.6 的这一步。 毕竟,商中的0 意味着十分位而非百分位。 一位一位向下平均分,看似啰嗦,但必须遵守,这正是数学学科必须讲究严谨精神的象征。
三是“如果商中这个0 不补会造成何种影响”的讨论。通过讨论,学生理解到仅仅漏了一个0,5 个0.01 就变成5个0.1,1.05 与1.5 可是完全不一样的结果。 可见,0 所引起的数位之差,不可小觑。
如此,通过上述三个问题的讨论,学生对“不够就移”有了更深刻的认识:不是随意就移,而是在补0 的基础上才移;学生也理解到,有些竖式省略了分0.6 的过程,但头脑中不能省略,做题时不能怕麻烦,尽量写清每一步,关注到每步先后顺利,这样就能够避免错误,有效杜绝作业中的失误现象。
(三)比较:明晰“加与不加”的区别
比较中寻方法,比较中找规律。 以比较为手段的思维方式,既是打破思维定势的需要,又是解决“老病根”与“并发症”的需要。商中间有0 的小数除法教学中,教师有意识地把漏掉0 或者不应有0 却补上了0 的错题呈现出来,同时呈现正确竖式,两两比较,引领学生明晰“加与不加”的区别,必能更好地帮助学生厘清相关概念,加深正确解题步骤的印象,提高学生的整体解题能力。
分析中,教师发问:“这个竖式的商中间为什么不能补0?”引领学生看一看商中的数位与下面的数位是不是有错位,是否有对应分的过程,学生自然而然明白问题出在哪里。教师应该多多出示这样的比较题型,通过细微的捕捉,“比”出问题的根源所在,“比”出正确的步骤,顺利地解决“老病根”与“并发症”。
通过上述三环节,学生在“商中间有0 小数除法”的练习中提高了正确率。 实践证明,商中间有0 小数除法的学习中,必须找准问题,分析根源,紧扣学情,采取针对性较强的对策,如整体把握,结构性迁移,真正厘清其中的内在机理,既防止“老病根”复发,又把“并发症”解决在萌芽状态。
