IWSNs防移动干扰节点的两层协作Stackelberg博弈

孙子文, 杨晨曦

(1. 江南大学物联网工程学院, 江苏 无锡 214122; 2. 物联网技术应用教育部工程研究中心, 江苏 无锡 214122)

0 引 言

工业无线传感器网络(industrial wireless sensor networks, IWSNs)具有自组织性和多跳特性,可用于工业生产和监控的工业数据的实时传输,可远程实时监控工业生产过程[1-2]。但受能量、连接性和安全性的限制,IWSNs面临来自无线通信信道的干扰攻击[3-4],尤其是具有随机性和灵活特性的移动干扰的攻击[5-7]。

移动干扰攻击与防御干扰两者之间的行为可视为一个博弈的过程。现有研究抵御移动干扰的文献较少,初步可查询到在随机移动攻击场景中,由边缘计算设备选取最佳协作节点发射干扰信号和合法节点共同抵御恶意攻击,来提高无线网络的安全速率[8]。描述博弈的方法主要为静态干扰攻击[9-10],将合法用户和智能干扰器的交互关系建模为Stackelberg博弈,采用最优功率分配算法得到最佳合法用户发射功率,以提高无线网络抗干扰能力[9];将攻击者和合法用户的竞争关系建模为联合博弈,通过提高合法用户的信干噪比(signal-to-interference-plus-noise-ratio, SINR)和降低攻击者的信号接收强度,求得博弈均衡条件,保证无线网络的安全速率[10]。目前缺乏通过将攻防双方的竞争行为建模为博弈模型并抵御移动攻击的方法,同时防御方被动参与博弈无法保证有效降低攻击方的干扰能力。

协作干扰技术利用无线信道的固有特性[11],协作方通过向攻击方发送反干扰信号,削弱攻击方的干扰攻击,降低防御方独自抵御攻击的损耗,有效保证通信安全[12-13]。通过建立多信道Stackelberg博弈模型,可保证传感器和控制器之间的信道传输安全[14]。为提高无线通信系统网络安全速率,建立非完全信息Stackelberg博弈,求解合法节点最佳功率[15]。为解决从控制器到执行器的下行链路通信安全问题,采用协作节点向攻击者发送干扰信号,以最大化提高合法通信信道的安全速率[16]。采用非合作博弈的人工干扰噪声策略对抗网络攻击,提高无线认知传感网络抵御隐私攻击的能力[17]。为提高车联网的安全性能,引入协作者向窃听信道发送干扰信号,建立平均安全速率,求出合法者和协作者的最佳功率[18]。利用协作干扰信号混淆无人机攻击方的信号,抵御无人机攻击[19]。在无协作前提下仅采用合法者与攻击者进行对抗博弈[14-15],合法者自身消耗较大,通过引入协作干扰技术[16-19],可降低消耗,但由于合法者之间的效益非均衡最优,无法保证长期稳定的协作,因此通信网络的安全速率无法保证。

为解决IWSNs物理层移动干扰攻击问题,本文将博弈论结合协作干扰技术,建立sink节点和簇头节点协作的两层Stackelberg博弈模型。以网络安全速率为优化目标,将sink节点、最佳协作节点和攻击节点之间的合作竞争关系建立为两层Stackelberg博弈,采用逆向归纳法求解sink节点最佳发送功率和协作节点最佳协作单价,提高协作节点积极性,提高IWSNs通信网络安全速率。

1 问题描述

1.1 网络模型

图1为IWSNs模型。

图1 IWSNs模型Fig.1 IWSNs model

设网络中有η个sink节点、N个簇头节点(包含N-1个协作干扰节点和1个发送节点i)、若干个普通节点和1个攻击节点。sink节点按照自身的路由路径移动,同时,收集一跳之内来自簇头节点的数据信息;簇头节点随机分布在sink节点的周围,收集簇内普通节点的数据信息并转发给就近的sink节点;攻击节点在移动过程中随机向通信范围内的sink节点发送干扰信号。被选为最佳协作节点的簇头节点J*,负责向攻击节点发送反干扰信号。

为排除信号衰落和噪声因素对模型的影响,假设以下前提条件:① 在整个IWSNs模型中,攻击节点处于随机干扰状态;② 所有节点端含有独立分布且具有相同方差的加性高斯白噪声。

1.2 干扰度量值

节点的干扰度量值是指节点受到邻居簇头节点信道干扰和自身自干扰对节点能量和传输功率的损耗。IWSNs中,节点采用电池供电,能量有限,且较大能耗的节点将加速剩余能量较小的节点死亡,故将节点剩余能量也作为节点的干扰度量。

考虑节点处于移动环境下,定义t时刻协作节点J的干扰度量值为

(1)

1.3 能量消耗模型

假设节点J每轮数据收集一跳通信范围内的簇头节点产生lbit的消息,则节点J接收到的信息量和节点J向其他K个邻居节点发送的信息量分别为

(2)

(3)

式中:ETNg,J表示节点对每条路径的期望传输次数,IEEE802.15.4规定数据发送次数最大不超过5[20],当ETNJ,g>5和ETNg,J>5,节点g和节点J不能相互通信。

假设节点单位时间内接收和发送lbit信息所耗能量分别为Er和Et,在每轮数据收集过程中,节点J发送和接收lbit数据时的能耗分别为

(4)

1.4 信道增益和信道容量

结合信道容量与SINR[21],描述IWSNs通信安全。

由文献[22]可得信道增益,则t时刻簇头节点i和攻击节点A到sink节点的信道增益、节点J到节点A和sink节点的信道增益分别为

(5)

(6)

(7)

(8)

从发送节点i到sink节点的SINR为

(9)

由香农定理,从节点i到sink节点的主信道容量为

Ci,s=B1log2(1+γi,s)

(10)

式中:B1为主信道带宽。

从攻击节点到sink节点的SINR为

(11)

由香农定理,从攻击节点到sink节点的干扰信道容量为

CA,s=B2log2(1+γA,s)

(12)

式中:B2为干扰信道带宽。

1.5 网络安全速率

以sink节点的抗干扰和攻击节点的攻击表征IWSNs安全性能,而sink节点的抗干扰和攻击节点的攻击分别体现为主信道容量和干扰信道容量,因此定义网络安全速率[23]为主信道容量和干扰信道容量的差值:

SRi=max(Ci,s-CA,s,0)

(13)

由式(13)可知,网络安全速率越高,说明主信道容量相比干扰信道容量越大,间接表明sink节点的抗干扰能力越强,攻击节点的干扰能力越弱。因此,可通过提高网络安全速率来提高sink节点的抗干扰能力,降低攻击节点的干扰能力。

(14)

1.6 协作节点选择方案

以IWSNs网络安全速率为优化目标,簇头节点在N-1个协作节点中选择最佳J*:

(15)

化简得到最佳协作节点J*:

(16)

研究对合法节点最不利的条件,即攻击节点可获得sink节点和协作节点的信道信息,同时预测二者的策略选择。研究式(14)的博弈策略可知:

(1) 攻击节点和sink节点具有竞争关系。sink节点为最大化IWSNs安全速率,选择数据发送功率以获得最大主信道容量;攻击节点根据预测到的sink节点的策略,选择最佳恶意干扰功率以获得最大干扰信道容量,以最小化IWSNs安全速率。

(2) 协作节点和sink节点具有竞争合作关系。为sink节点和协作节点的合作关系长久保持,sink节点需要向协作节点支付报酬,以激励协作节点共同合作抵御攻击。对sink节点,为最大化IWSNs安全速率,需要选择最佳发送功率,同时向协作节点购买最佳协作干扰功率;由于提供协作功率所需付出的额外消耗,协作节点为达到收支平衡,选择最佳协作干扰功率单价。

由分析可知,研究利用两层协作Stackelberg博弈模型分析sink节点、攻击节点和协作节点之间的多层竞争合作关系。

2 两层Stackelberg博弈模型

2.1 防移动干扰攻击的两层Stackelberg博弈建模

根据协作节点共同防御移动干扰攻击的方案中的两层嵌套竞争和合作关系,在第一层Stackelberg博弈中,将攻击节点设置为领导者,将sink节点设置为跟随者;在第二层Stackelberg博弈中,将最佳协作节点设置为领导者,将sink节点设置为跟随者。建立两层协作Stackelberg博弈模型:

G=[{A,J*,s},{PA,μ,(Ps,PJ*)},{UA,UJ,Us}]

(17)

两层协作Stackelberg博弈模型包含3个阶段,如图2所示。

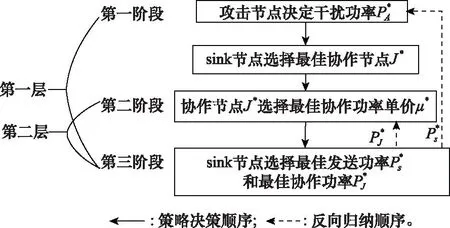
图2 两层协作Stackelberg博弈模型Fig.2 Two-layer cooperative Stackelberg game model

两层协作Stackelberg博弈是经典Stackelberg博弈的多层嵌套[24],第一层博弈领导者攻击节点同时也是第二层博弈的领导者,根据上一轮sink节点的策略选择自身的攻击功率;最佳协作节点作为第二层博弈的领导者,通过观察攻击节点的策略,调整协作功率单价;sink节点作为第一层和第二层博弈领导者的跟随者,通过观察两个领导者的策略做出最佳选择。第一层和第二层的博弈者之间按照决策顺序参与博弈,形成嵌套关系,相互影响,相互制约,直至三方选择出符合自身利益最大化原则的决策。

第一阶段:对攻击节点,为最小化网络安全速率,同时考虑到自身受到的信道干扰和能量消耗,设计效用函数如下:

(18)

式中:第1项表示攻击节点通过增加干扰信道容量使得网络安全速率降低后的收益,安全速率越低,攻击节点收益越大;第2项表示攻击节点的能量消耗;第3项表示攻击节点的信道干扰度量值。

由式(18),解决问题式(19)可得最佳干扰攻击功率:

(19)

第二阶段:对最佳协作节点J*,有偿对sink节点提供协作服务,同时考虑协作后的能量消耗和信道干扰度量值,设计效用函数如下:

(20)

式中:第1项表示节点J*提供服务后的收益;第2项表示节点J*的能量消耗;第3项表示节点J*的信道干扰度量值。

由式(20),解决问题式(21)可得最佳协作干扰功率单价:

(21)

第三阶段:对sink节点,为最大化网络安全速率,同时考虑到节点的能量消耗和信道干扰度量值,设计效用函数如下:

(22)

式中:第1项表示sink节点提高安全速率获得的收益;第2项表示节点的能量消耗;第3项表示节点的信道干扰度量值;第4项为sink节点付给协作节点的报酬。

由式(22),解决问题式(23)可得sink节点最佳数据发送功率和最佳协作功率:

(23)

2.2 防移动干扰攻击的两层Stackelberg博弈均衡分析

安全速率式(13)经博弈建模转化为3个节点的效用函数最大化问题,分别为式(19)、式(21)和式(23)的3个子优化问题,子优化问题的解即为博弈均衡解。

2.2.1 sink节点最佳策略分析

sink节点为最大化主信道容量,考虑节点的能量消耗和信道干扰,问题式(23)可转化为问题式(24):

(24)

(25)

(26)

(27)

(28)

(29)

证明由式(24)和式(27)得到相应的海塞矩阵:

(30)

式中:

证毕

2.2.2 最佳协作节点的最佳策略分析

(31)

令式(31)等于0,得μ*的均衡解为

(32)

当μ*<0时,协作节点认为需无偿提供协作干扰功率到攻击节点,这种情况不符合现实场景,本文不讨论此条件。

2.2.3 攻击节点的最佳策略分析

攻击节点以最大化干扰信道容量为优化目标,选择最佳恶意干扰功率,考虑到能量消耗和信道干扰,优化问题式(19)可转化为

(33)

(34)

(35)

Stackelberg博弈是一种完全信息的动态博弈,采用逆向归纳法求解Stackelberg博弈均衡解,可体现博弈动态性,同时降低博弈中不可信的策略选择,提高博弈均衡解的准确性。

2.3 博弈均衡解分析流程

防移动干扰攻击的两层博弈模型均衡解的分析流程如图3所示。

图3 博弈均衡解的分析流程Fig.3 Analysis process for game equilibrium solution

该分析流程主要分为以下几个步骤:

步骤 1初始化

步骤 2循环迭代

步骤 2.4循环迭代,t=t+1。

3 仿真与分析

使用软件进行仿真分析,参数配置如表1所示,其中sink节点和攻击节点在移动过程中的路由协议参考低延迟最佳链路状态路由[26],噪声方差归一化为1×10-3[27]。移动路由协议采用低延迟最佳链路状态路由(low latency-optimized link state routing, LL-OLSR)。

表1 仿真参数Table 1 Simulation parameters

3.1 算法性能分析

选取sink节点发送功率和效用函数、攻击节点效用函数和协作节点的协作功率为评价指标,攻击节点和sink节点的初始位置随机设为(0,0)和(40,0),由式(5)～式(8),在节点区域内随机选取6组攻击节点和sink节点之间距离由近及远的位置坐标,分析sink节点有簇头节点协作和无簇头节点协作时的发送功率,仿真结果如图4、图5和表2、表3所示。

表2 不同位置坐标对的节点协作干扰功率Table 2 Cooperative interference power of cooperative nodes of coordinate pairs of different positions W

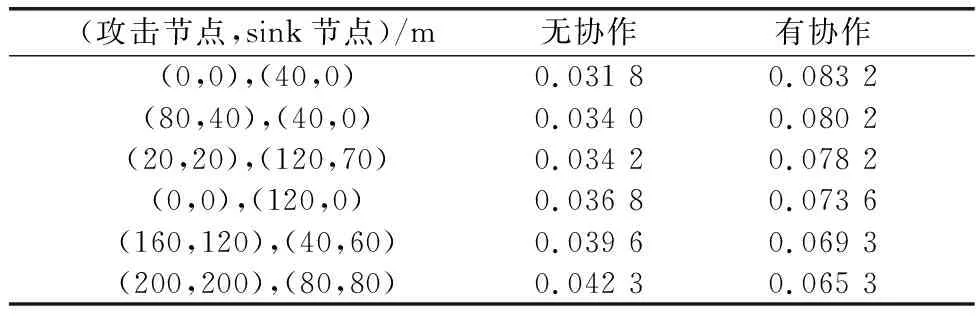
表3 有无协作时不同位置坐标对的sink节点发送功率Table 3 Sending power of sink node of different coordinate pairs of different positions with or without collaboration W

图4 不同位置坐标对的sink节点效用函数Fig.4 Utility function of sink node of coordinate pairs of different positions

图5 不同位置坐标对的攻击节点效用函数Fig.5 Utility function of attack node of coordinate pairs of different positions

由图4和图5可知,sink节点和攻击节点距离较近的效用函数值低于距离较远的效用函数值,这是因为距离较近时,sink节点接收攻击节点的信号强度高于距离较远时的信号强度,受到的干扰更大。攻击节点在距离sink节点较近的效用函数值高于距离较远的效用函数值,这是因为距离较近时,攻击节点更易攻击到sink节点,效用函数也更高。

由表2可知,sink节点距离攻击节点较近时,sink节点采取积极的防御策略,向协作节点购买的协作功率降低;sink节点距离攻击节点较远时,sink节点采取消极的防御策略,向协作节点购买的协作功率增加。因此,协作节点起到了防御攻击节点的作用。

表3对比分析了有无协作时sink节点的发送功率。在无协作节点时,sink节点在距离攻击节点较远的位置获得较大的发送功率,这是因为攻击节点远离sink节点较远时,发射的干扰信号较弱,sink节点的发送功率得到提高;在有簇头节点作为协作节点时,sink节点在距离攻击节点较远时获得较小的发送功率,这是因为攻击节点远离sink节点时,协作节点通过发射反干扰信号给攻击节点,使sink节点在发射功率较小的条件下完成数据收集过程。总之,sink节点在有协作条件下的发送功率比无协作时平均提升了101.5%。

3.2 安全性能分析

分析本文方案在网络安全速率方面的性能,选取网络安全速率为评价指标,将无协作干扰(no cooperative jamming, NCJ)方案和边缘计算设备协作方案[8]进行仿真对比分析,结果如图6所示。

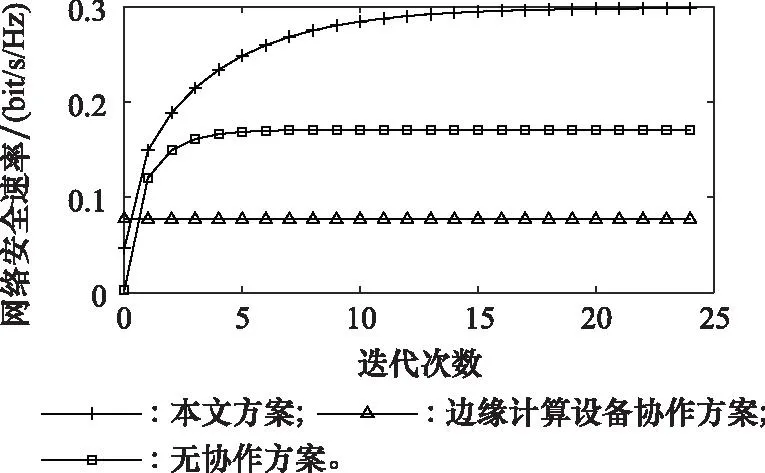
图6 不同方案的网络安全速率Fig.6 Network security rates of different schemes

由图6可知,NCJ方案和边缘计算设备协作方案的网络安全速率均低于本文所提协作节点选择方案,这是因为NCJ方案中的合法节点只依靠自身功率和能量抵御攻击节点,边缘计算设备协作方案采用边缘设备选择协作节点,大大增加了协作成本,导致协作节点服务积极性不高,协作节点选择方案选取对攻击节点干扰程度最大且对sink节点影响最低的协作节点,在降低干扰信道容量的同时降低了对主信道容量的影响。

分析sink节点抗干扰性能的提升,选取sink节点效用函数为评价指标,与基于抗干扰信道的积极吸引[28](active attraction based anti-jamming channel access, 3ACA)算法、基于博弈的信道分配[29](channel allocation based on Stackelberg game, CASG)算法和纳什讨价还价博弈[30](Nash bargaining game, NBG)算法进行仿真对比分析,结果如图7所示。

图7 不同方案的sink节点效用函数Fig.7 Utility function of sink node of different schemes

由图7可知,本文方案的sink节点效用函数值高于其他3种方案。这是因为3ACA算法和CASG算法以牺牲节点的信道访问方式为代价,且没有其他抗干扰技术共同抵御攻击,NBG模型中博弈双方在未考虑彼此策略的前提下独立且同步地进行决策,无法保证合法节点的收益函数。本文所提sink节点通过购买协作功率获得协作节点有偿服务,实现了效用函数的最大化。

4 结 论

针对IWSNs物理层抵御移动干扰攻击节点的安全问题,研究sink节点和簇头节点共同协作的两层抗干扰博弈模型。首先,利用协作干扰技术在簇头节点中选择最佳协作节点,共同抵御移动干扰节点。其次,利用两层Stackelberg博弈模型为sink节点、最佳协作节点和攻击节点之间的合作竞争关系行为建模,以网络安全速率为优化目标,采用逆向归纳法求解博弈均衡解。仿真结果表明,与其他博弈模型相比,本文采用的协作节点选择方案对移动攻击节点的抵御效果更佳,两层协作Stackelberg博弈模型可有效提高通信网络安全速率。