空中目标动态HRRP特征可重构模拟方法

徐 勇, 冯德军, 王俊杰, 徐志明, 隋 冉

(国防科技大学电子科学学院, 湖南 长沙 410073)

0 引 言

随着技术的发展,无论是在民用或是在军事领域中,空中目标都越来越普遍,如无人机、直升机、战斗机等,其已经成为雷达探测的主要目标之一。与地面固定目标不同,随着雷达与目标相对运动状态的变化,空中目标的雷达电磁特征也是动态变化的,其特征较为复杂[1-3]。而在雷达系统测试、电子对抗防护等领域中,为了构建逼真的电磁环境,往往需要对目标的雷达电磁特征进行精确的模拟[4],空中目标的动态电磁特征正是目前雷达目标模拟技术领域的关键难题之一。

目前的雷达目标模拟技术可以分为有源和无源两类。有源模拟技术可以生成较为精确的目标特征,然而其成本较高,计算复杂,不易于灵活布置[5-9]。而无源模拟技术并不需要主动发射电磁波信号,只需要将无源器件放入指定区域,使其产生的回波与真实目标回波相似,即可达到目标模拟的目的[10-13]。例如,利用箔条模拟空中威胁目标[10],吸引对方雷达系统的注意力;利用小型靶标加载龙伯透镜反射器模拟空袭武器雷达散射截面[11];利用角反射器阵列模拟电磁靶船[12]等。Luo等[13]提出了一种使用不同尺寸的角反射器阵列来模拟真实舰船目标的方法,不同尺寸角反射器分布在不同位置,能够形成与真实目标相似的一维高分辨距离像(high resolution range profile, HRRP)结果,产生更加逼真的模拟效果。然而,传统无源器件在加工完成后,其雷达特征无法改变。因此,上述研究均只针对固定的目标特征进行模拟,针对空中目标的动态电磁特征模拟的研究较少。

可调控电磁超表面技术的问世为雷达目标模拟技术领域的难题带来了可能的解决方案。电磁超表面是一种人为加工设计出来并具有自然界材料所不具备的奇特电磁特征的复合材料[14-16]。可调控技术是指在电磁超表面加入可调器件,通过外加激励实现对超表面特征的灵活调控。可调控电磁超表面的可设计性、可灵活调控性使得其在多个领域都成为了热点研究话题。随着可调控电磁超表面技术的不断发展,各种新型材料相继问世,频率选择表面[17-20]、相位调制表面(phase-switched screen, PSS)[21-24]、完美吸波体[25-27]、编码超表面[28-30]等多种新型超表面材料已经具备了对雷达回波多个维度的精准调控能力。Xu等[31]提出了一种利用PSS对雷达反射信号进行相位调制的方法,该方法能够将雷达入射信号的能量进行重新分配,在入射信号频点两端产生对称的谐波分量。可调控电磁超表面的调控能力使得其能够实现电磁特征可重构的模拟效果,同时又保持着传统无源器件的优势,成本低、布置灵活。这些特点使得可调控电磁超表面能够被很好地应用于雷达目标模拟技术领域。

基于上述思想,本文提出了一种基于PSS的空中目标动态HRRP特征可重构模拟方法。PSS通过其对雷达入射波的调制作用,能够生成可控的谐波分量。通过对调制信号的设计,使得生成的谐波分量可以随时间变化,其变化规律与目标动态HRRP特征变化规律相似,从而实现目标动态HRRP特征的模拟效果。本文第1节以无人直升机旋翼为例,对其旋翼的运动状态进行了建模,并分析了其在不同运动参数下的动态HRRP特征规律。第2节对可重构模拟技术理论进行了介绍,分析了周期信号调控下,PSS的调制频率对调制效果的影响。根据PSS对雷达入射波的调制效果,提出了调制频率时变的PSS调制模拟方法,该方法生成的谐波分量位置随时间变化规律与无人直升机旋翼的动态HRRP特征变换规律相似。第3节利用Matlab软件对模拟效果进行仿真分析,并对模拟误差进行了计算,最后考虑了信噪比(signal to noise ratio, SNR)对模拟效果的影响。第4节对本文的主要内容进行了总结。

1 目标动态HRRP特征分析

1.1 目标运动状态建模

无人直升机在运动过程中,其动态电磁特征主要包含两个方面,一是无人直升机整体平动带来的多普勒频移,主要包含了无人直升机运动的速度信息;二是无人直升机旋翼旋转带来的多普勒信息,主要包含了无人直升机旋翼的精细结构特征,这些结构特征对无人直升机的识别具有重要意义。本文主要针对无人直升机旋翼的动态HRRP特征进行分析。

以双旋翼无人直升机为例,由于旋翼长度大于雷达入射波波长,因此旋翼叶片的散射可以看作是多个散射点的散射场的叠加。取叶片最外端的两个散射点进行建模,将其简化为两个点目标的旋转运动。假设叶片长度为1 m,两个点目标之间的距离则为L=2 m,初始位置分别设为A(-0.5L,0)和B(0.5L,0),其分别围绕中心点O(0,0)进行匀速旋转运动,旋转角速度为ω=2 π rad/s,如图1所示。

图1 直升机旋翼等效运动模型Fig.1 Equivalent motion model of helicopter rotors

根据二维欧拉旋转矩阵可知,当目标初始位置为M(x1,y1),旋转中心位置为O(x0,y0),旋转角速度为ω时,任意时刻t的目标位置可表示为

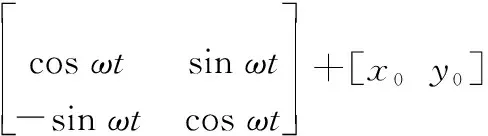
(1)

按照式(1)可知,任意时刻点目标A和B的位置可表示为

(2)

(3)

1.2 目标动态HRRP特征分析

图2 目标与雷达的空间相对位置Fig.2 Relative position of target and radar in space

根据式(2)和式(3),可以计算目标与雷达的实时距离为

(4)

雷达采用线性调频(linear frequency modulation, LFM)体制雷达,其发射信号为

(5)

式中:Tp为发射信号的脉冲宽度;fc为信号中心频率;Kr=Bw/Tp为信号的调频斜率,Bw为信号带宽。

采用Matlab仿真软件对目标的动态HRRP特征进行仿真,雷达系统仿真参数如表1所示。

表1 雷达系统仿真参数Table 1 Radar system simulation parameters

采用脉冲压缩技术检测目标的动态HRRP特征,检测结果如图3所示。

图3 目标动态HRRP特征仿真结果Fig.3 Simulation results of dynamic HRRP feature of targets

从仿真结果可以看出,随着时间的变化,目标的HRRP特征呈现周期性变化。目标检测峰值位置在旋转中心附近呈周期变化,变化范围为(-0.7 m,0.7 m)。与式(4)计算结果一致,变化周期为1 s,与角速度ω=2 π rad/s相符。当t=0 s时,两目标之间的相对距离最远,随着时间的增加,目标的相对距离减小。当t=0.25 s时,两个目标与雷达距离相等,两个回波叠加为一个回波,回波幅度变大。在这之后,目标相对距离又会增加,呈现周期变化,与第1.1节中所设目标运动模型相符。

分别改变目标间距L和旋转角速度ω。仿真结果如图4所示。与图3相比,当目标间距L增大时,目标HRRP变化范围增大。当L=4 m时,变化范围为(-1.4 m,1.4 m)。当旋转角速度ω增大时,HRRP变化周期会变小,当ω=5×2 π rad/s时,变化周期为0.2 s。

图4 不同运动参数下的目标动态HRRP特征仿真结果Fig.4 Simulation results of dynamic HRRP feature of targets with different motion parameters

2 可重构模拟技术理论分析

2.1 PSS调控效果分析

PSS是一种新型的超表面结构,主要由可调控阻抗层、介质层和金属底板层构成,如图5所示。可调控阻抗层包含可调控器件,能够改变阻抗层的散射状态,使得其可在全反射和全透射状态间切换。这种切换能够实现频谱搬移的效果,在原始入射波载频处信号能量为零,载频附近生成可控的谐波分量,调控效果能够被很好地用来实现空中目标动态HRRP特征的可重构模拟。

假设入射电磁波的载频为fc、波长为λ,入射角度为90°垂直入射。PSS介质层的介电常数为1、厚度为d=λ/4。当可调控阻抗层为全反射状态时,从PSS阻抗层反射的电磁波可表示为cos(fct)。当可调控阻抗层为全透射状态时,电磁波完全穿过阻抗层并经金属底板层反射,此时反射波可以表示为cos(fct+2βd)=-cos(fct),其中波数表示为β=2π/λ,两种状态下的反射电磁波相位相反。

当PSS的状态在全反射状态和全透射状态之间周期切换时,可以等效为PSS对入射电磁波施加了一个双极性周期矩形脉冲形式的相位调制信号,调制信号模型如图6所示,其幅值在+1和-1之间变换。

图6 PSS相位调制信号模型Fig.6 PSS phase modulation signal model

将状态周期变化的PSS等效为周期调制信号,其时域信号可以用傅里叶级数表示为

(6)

式中:A0=|2τ/T-1|,An=(1/nπ)(1-cos(2nπτ/T))。τ表示+1的驻留时间,T为调制信号周期,fs=1/T为调制频率,τ/T为调制信号的占空比。信号频谱可表示为

(7)

当入射电磁波s(t)垂直照射到PSS上时,其反射信号时域可以表示为

r(t)=s(t)·p(t)

(8)

反射信号频谱为

(9)

根据式(9)可知,PSS的调制效果为在中心频率附近生成许多对称的谐波分量ΣS(f-nfs),当调制信号的占空比τ/T=0.5时,A0=|2τ/T-1|=0,原入射信号中心频率所在位置的输出峰值为0,An=(1/nπ)(1-cos(2nπτ/T))=(1/nπ)(1-cos(nπ)),其偶次谐波分量也为0,只有奇次谐波分量,且其幅值逐渐减小。其谐波生成位置与调制频率fs有关,不同调制频率能够产生不同位置的谐波分量,如图7所示。

图7 调制频率对谐波位置的影响Fig.7 Effect of modulation frequency on harmonic position

2.2 目标动态HRRP特征模拟原理

以LEM雷达为例,其发射信号s(t)如式(5)所示。LEM信号经过PSS调制后,返回雷达接收机,经混频和滤波处理后,反射信号变为基带信号,其可以表示为

(10)

(11)

当调制信号占空比为0.5时,A0=0,PSS原始中心位置输出为0,在其附近位置输出对称的谐波分量,第n阶谐波分量位置为

(12)

式中:tpeak为谐波分量出现的时间;c为光速。

由式(12)可知,PSS生成的谐波位置与调制频率fs有关。由于其高次谐波分量与一阶谐波分量相比,幅值较低,当忽略其余高次谐波分量时,则一阶谐波分量位置为

(13)

目标的位置随时间呈现周期性变化,如式(2)和式(3)所示,由于其是对称的,定义目标与旋转中心位置的距离为ΔR(t)。PSS能够改变调制频率,从而实现对生成的谐波分量位置的控制。想要模拟不同时刻目标位置的变化规律,则要求不同时刻调制频率与生成谐波分量位置的关系为

(14)

以一个雷达脉冲信号周期为时间间隔,忽略脉冲内目标位置的变化,在不同脉冲信号之间,调制频率是不同的,则调制信号更改为

(15)

式中:tk=kT为第k个脉冲发射时刻,T为脉冲发射周期,k是一个正整数,代表发射的脉冲数。调制频率时变的调制信号模型如图8所示。

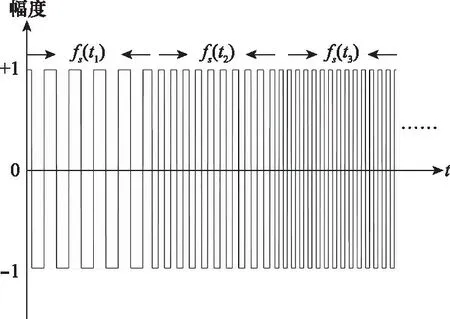
图8 调制频率时变的调制信号模型Fig.8 Modulation signal model with time-varying modulation frequency

根据式(2)～式(4)和式(14),调制频率的表达式如下所示:

(16)

当采用调制频率时变的调制信号控制PSS的状态切换时,由于调制频率的变化,其生成的谐波位置也在发生变化,根据式(13)和式(14)可知:

(17)

PSS调制效果产生的一阶谐波分量位置与实际目标所在位置一致,这就实现了目标动态HRRP特征的模拟。

3 模拟效果分析

3.1 不同运动参数下的目标动态HRRP特征模拟

由第2节的分析可知,PSS对入射电磁波的调制效果为消隐其中心频率分量,在其附近生成多个对称的谐波分量,同时可以通过调制频率的变化控制生成谐波分量的位置。将谐波分量的位置分布规律调控为与第1节中分析的目标动态HRRP特征变化的规律相同,即可实现目标的动态HRRP特征模拟。

采用Matlab仿真软件对模拟效果进行分析,目标参数设置和雷达参数设置与第1节一致,将PSS调制信号设置为调制频率时变的双极性周期脉冲信号,其表达式如式(15)所示,其占空比为0.5,调制频率随时间变化,如式(16)所示。当L=2 m,ω=2 π rad/s时,根据式(16)计算可得所需的调制频率变化区间为(0,233)kHz。将PSS反射率设置为实际目标的2倍,以模拟2个目标重合时的雷达散射截面(radar cross section, RCS)大小。仿真模拟结果如图9所示。

图9 目标动态HRRP特征模拟效果Fig.9 Simulation effect of dynamic HRRP feature of targets

由图9可知,目标动态HRRP特征模拟效果与图3真实目标的动态HRRP特征变化规律一致,多余的高阶谐波分量由于幅值很小,可以忽略不计。

定义目标实际HRRP归一化幅值大小为E_t(t,r),t为动态HRRP特征的时间变化范围,取(0,2) s,r为HRRP的距离轴,取值范围为(-4,4)m。定义模拟HRRP归一化幅值大小为E_s(t,r)。则模拟绝对误差可以表示为

Error(t,r)=|E_s(t,r)-E_t(t,r)|

(18)

误差计算结果如图10所示。

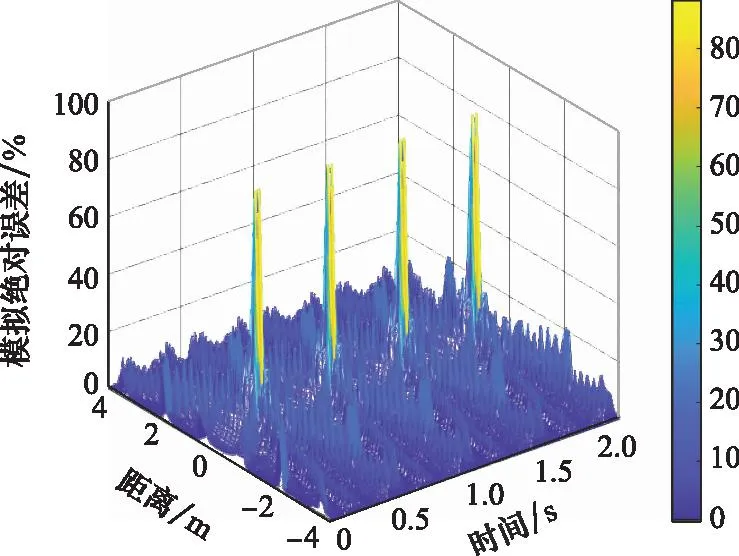
图10 模拟效果的绝对误差计算结果Fig.10 Calculation results of simulation effect absolute error

从图10可以看出,t=0.25 s,t=0.75 s,t=1.25 s和t=1.75 s附近误差较大,这是由于此时两个点目标距离过近。由式(14)可知,目标距离越近,所需的调制频率越小,当调制频率小于20 kHz时,PSS调制信号失去调制效果,表现为在实际PSS位置处检测到信号,没有其他谐波产生,此时的模拟效果失效,导致误差急剧增大。调制频率小于20 kHz对应的目标间距约为±0.05 m,因此当ΔR(t)<0.05 m时,模拟误差约为80%,无法实现目标的HRRP特征模拟。当目标间距ΔR(t)>0.05 m时,由图10可知,在PSS调制产生高次谐波的位置,模拟绝对误差在20%左右,其他区域模拟绝对误差在10%左右。

当目标运动参数发生变化时,可以根据式(16)改变PSS调制信号的调制频率,从而实现不同运动参数下的目标动态HRRP特征模拟。当目标参数变为L=4 m,ω=2 π rad/s和L=2 m,ω=5×2 π rad/s时,模拟结果如图11所示。

图11 不同运动参数下的目标动态HRRP特征模拟效果Fig.11 Simulation effect of dynamic HRRP feature of targets with different motion parameters

通过控制调制频率的变化,不同运动参数下的目标动态HRRP特征也可以被模拟,其误差情况与图10类似,在此不再分析。

3.2 不同SNR下的目标动态HRRP特征模拟

上述分析均是基于最理想的情况,然而在实际情况下,雷达系统和自然环境中都会存在噪声,接下来分析噪声对目标动态HRRP特征模拟的影响。

对目标实际信号和模拟信号添加高斯白噪声,采用仿真软件对模拟效果进行分析,其余参数设置保持不变,设置SNR=20 dB,目标动态HRRP特征模拟效果及误差如图12所示。

图12 目标实际动态HRRP特征模拟效果及绝对误差计算结果Fig.12 Simulation effect of target actual dynamic HRRP feature and calculation results of absolute error

与图3、图9和图10相比,SNR为20 dB时,噪声对目标模拟的影响几乎可以忽略不计,模拟误差情况与无噪声时类似。

改变SNR大小,不同SNR下的目标模拟效果的绝对误差计算结果如图13所示。

图13 不同SNR下的目标模拟效果的绝对误差计算结果Fig.13 Calculation results of absolute error of target simulation effect with different SNRs

从图13可以看出,随着SNR的减小,相对噪声能量增大,模拟误差也在增大。其中,ΔR(t)<0.05 m时的误差是由PSS调制原理引起的,与噪声无关,因此随着SNR的变化,该部分区域的误差不变。在其他时间区域内,随着SNR的减小,高阶谐波分量所在位置引起的误差在减小。这是由于SNR越小,相对噪声能量越大,这使得高阶谐波分量被淹没在噪声中,减小了模拟误差。非高阶谐波分量位置处的模拟误差会随着噪声的增大而增大,因此总体的模拟误差随着SNR的减小而增大。

4 结 论

本文提出了一种基于PSS的空中目标动态HRRP特征可重构模拟方法。以无人直升机旋翼的旋转运动为例,通过运动建模和仿真分析可知,其HRRP特征呈现周期性变化。为了实现这种动态HRRP特征的模拟,本文提出了调制频率时变的PSS调控方法。通过对PSS调制信号进行设计,使得其调制效果为产生位置随时间变化的可控谐波分量,这种调制效果可以实现空中目标的动态HRRP特征模拟。仿真结果表明,由调制频率时变的PSS调控方法模拟的动态HRRP特征与真实无人直升机旋翼的动态HRRP特征基本一致。另外,由于调控方法的不足,在某些时刻,模拟绝对误差过大,但在其他时刻的模拟绝对误差均小于10%,模拟效果逼真。随着SNR的减小,模拟误差会逐渐增大。本文所提方法为无源电磁调控目标动态特征模拟提供了新的方案,对实现结构简单、布置灵活、可实时重构的雷达目标特征模拟技术研究而言具有借鉴意义。