地形遮蔽下的电磁波绕射效应对机载电子战影响

张施雨, 吴 煜, 熊怡因

(中国电子科技集团公司第二十九研究所, 四川 成都 610036)

0 引 言

现代信息化战场上,机载电子战设备担负着监视战场电磁态势、夺取战场制电磁权的重要使命[1]。受机载电子战设备与地面雷达视距连线内的山岗、丘陵等遮蔽物影响[2-5],即使两者之间的距离在理论视距范围内,通视条件往往无法形成[6-8]。这时,由于电磁波绕射效应[9-11],机载电子战设备不一定会完全丧失侦察、干扰功能,但是随着绕射效应下电磁波空间传输损耗增大,其效能会下降[12-14]。

国内外在定量评估山峰绕射造成的电磁波传输损耗时,一般采用刃型绕射模型[15-19]。机载电子战典型作战距离达到数百千米,电子战设备与雷达之间往往会遇到两个及两个以上山峰的阻挡,这种情况在高山起伏的山区或丘陵地带相当普遍。国内外研究双/多峰绕射的模型主要有Bullington模型[20]、Epstein-Peterson模型[21]以及Picquenard模型[22]。常规的Bullington模型适应复杂环境的能力不强;Epstein-Peterson模型在两个刃形山峰距离较远时提供了良好的计算精度,但在两个山峰较近时精度较差;Picquenard模型适用性广,对远、近山峰均有良好的计算精度,因而被广泛应用于工程计算中,并推广至刃形多峰绕射模型中[23-29]。在机载电子战相距数百千米的对抗场景下,地球曲率对绕射模型的影响不可忽略,传统的文献缺乏针对此场景的研究。

本文研究了地形遮蔽条件下电磁波绕射效应对机载电子战的影响,主要工作分为如下3点:其一是根据地球曲率提出了基于传统刃形单峰绕射模型的山峰绕射高度算法;其二是根据地球曲率提出了基于Picquenard刃形多峰绕射模型的主峰迭代搜索算法,并利用试验实测数据验证了算法的正确性;其三是基于地形遮蔽条件下电磁波绕射效应提出了机载电子战作战应对策略。

1 地形遮蔽下电磁波绕射模型

1.1 基于地球曲率的刃形单峰绕射模型

在经典的电磁理论中,通常用电磁波衰减因子A表征单峰绕射后电磁波的传输衰减:

(1)

式中:E0为无刃形屏障时的自由空间场强;E为电磁波绕射后场强。

工程计算上通常利用下列代数近似计算A[30-31]:

(2)

式中:υ为几何尺度因子[30-31],其定义为

(3)

式中:d1、d2分别是雷达、机载电子战设备到屏障平面的距离;hp是山峰绕射高度,即屏障顶至雷达、机载电子战设备连线的距离。hp<0时,υ为负值,场强随υ的变化而围绕着自由空间场强E0上下波动;hp>0时,阴影区场强呈单调变化;hp=0时,直射线掠过障碍顶点时,场强恰好是自由空间场强值的一半,绕射损失为6 dB。

考虑到地球曲率,本文提出了一种直接通过几何关系解算山峰绕射高度hp的算法,如图1所示。

图1 地球曲率下计算山峰绕射高度Fig.1 Diffraction height of mountain peaks with the curvature of the Earth

(4)

(5)

(6)

式中:H1、H2分别是雷达、机载电子战设备绝对高程;Hp是屏障绝对高程;D1、D2分别是雷达、机载电子战设备到屏障平面地表距离。

1.2 基于地球曲率的刃形多峰绕射模型

多峰绕射Picquenard模型由其双峰绕射模型推广而来。双峰模式下,首先选取双峰中比较高的作为主峰,在假定其他山峰不存在的情况下,按照单峰模型计算主峰的绕射高度hp1及d1、d2,计算单峰绕射损耗A1,然后主峰和较远天线直线相交,求得第二峰的绕射高度hp2,计算其绕射损耗A2,总绕射损耗为A1+A2。

将Picquenard模型推广至多峰绕射后,第一步也即最重要的一步是对主峰多次进行迭代排序,筛选出每一步计算时的主峰、次峰。在收发天线距离不远时,由地球曲率带来的影响可以忽略,主峰与次峰之间的关系可由其高程数据表征。然而,机载电子战设备通常在距雷达数百千米外进行电子对抗,受地球曲率影响,主峰的筛选与山峰距雷达距离、山峰高程等综合因素相关。

本文提出了一种基于雷达上视角的主峰搜索算法,以解决地球曲率影响下Picquenard模型迭代搜索主/从峰的难题。雷达在观测不同高度的目标时,其发射电磁波方向与地平线间的夹角也称雷达上视观测角θ1。电磁波到达被观测目标的方向与地平线之间的夹角也称下视观测角θ2。如图2所示,雷达与目标地表距离为D,对应地心张角α。

图2 无折射条件下地面雷达上视观测角Fig.2 Observation angle on ground radar with non refractive condition

由几何关系可得

(7)

式中:α=D/R;θ2=θ1+α。化简后可得无折射条件下雷达对目标上视观测角为

(8)

电磁波在均匀大气中传播使其射线轨迹为直线,但实际上大气是不均匀的,其折射指数随高度变化,这导致电磁波在大气中的传播轨迹是弯曲的。文献[32-33]引入了等效地球半径Re的概念,用于替代地球实际半径R,此时非均匀大气可被等效为均匀大气,弯曲的射线被看作直线处理。地球等效半径Re与地球半径R之比为等效地球半径因子K,即K=Re/R。

补偿大气折射后,雷达上视观测角θ1为

(9)

1.3 Picquenard模型主峰迭代搜索算法

将上述雷达上视角计算方法应用到Picquenard模型,图3给出了以4个山峰屏障为例的多峰绕射模型,Hp1～Hp4分别为4个屏障高程,D1～D5分别为雷达与雷达之间、各个屏障之间、各个机载电子战设备之间的地表距离。

图3 Picquenard模型雷达上视观测角应用Fig.3 Application of Picquenard model radar for observation angle

基于Picquenard模型推广到地球曲面下的多峰绕射模型具体实现步骤如下。

步骤 1利用本文计算方法得出位于雷达与机载电子战设备之间各屏障的上视观测角θ1～θ4,选出具有最大观测角θ3的屏障3作为主峰1,计算其绕射高度hp3。

步骤 2去掉次峰屏障1、次峰屏障2、次峰屏障4后简化为单峰绕射模型,计算绕射损耗A1,其中d1=(R+H1)·sin[(D1+D2+D3)/R],d2=(R+H2)sin[(D4+D5)/R]。

步骤 4去掉次峰屏障2、次峰屏障4后建立雷达与主峰屏障3之间关于次峰屏障1的单峰绕射模型,计算绕射损耗A2-1,其中d1=(R+H1)sin(D1/R),d2=(R+Hp3)·sin[(D2+D3)/R]。

图4 次主峰选择中雷达上视观测角的应用Fig.4 Application of observation angle in secondary peak selection

步骤 6去掉次峰屏障1、次峰屏障2后建立主峰屏障3与机载电子战设备之间关于次峰屏障4的单峰绕射模型,计算绕射损耗A2-2,其中d1=(R+Hp1)sin(D4/R),d2=(R+H2)sin(D5/R)。

步骤 8去掉次峰屏障4后建立次主峰屏障1与主峰屏障3之间关于次峰屏障2的单峰绕射模型,计算绕射损耗A3-1,其中d1=(R+Hp1)sin(D2/R),d2=(R+Hp3)·sin(D3/R)。

步骤 9求出雷达与机载电子战设备总绕射损耗A=A1+A2-1+A2-2+A3-1。

2 绕射效应对机载电子战影响的仿真分析

2.1 刃形单峰绕射

固定屏障距雷达距离、机载电子战设备高程,研究屏障高程、雷达与机载电子战设备位置关系对电磁波传输损耗的影响情况。雷达高程为10 m,机载电子战设备高程为6 000 m,雷达载频为3 000 MHz,屏障距雷达20 km,屏障高程为0～1 500 m,电磁波传输损耗随距离(视距331.9 km内)的变化情况如图5所示。

图5 雷达高程为10 m时的电磁波传输损耗情况Fig.5 Electromagnetic wave transmission loss situation with radar elevation of 10 m

雷达高程为500 m,屏障高程为400～1 500 m,其他条件不变,电磁波传输损耗随距离的变化情况如图6所示。

图6 雷达高程为500 m时的电磁波传输损耗情况Fig.6 Electromagnetic wave transmission loss situation with radar elevation of 500 m

固定机载电子战设备阵位研究屏障高程、距离雷达位置对机载电子战设备侦收的影响情况,雷达高程为500 m,机载电子战设备距雷达300 km,屏障高程为400～1 000 m,其他条件不变,电磁波传输损耗随屏障距雷达距离的变化情况如图7所示。

图7 不同高程屏障、距雷达不同距离下电磁波传输损耗情况Fig.7 Electromagnetic wave transmission loss situation with different elevation barriers and radar distances

2.2 刃形多峰绕射

固定雷达高程、机载电子战设备高程、屏障与雷达位置关系,研究多个不同高程屏障下,雷达与机载电子战设备位置关系对电磁波传输损耗的影响情况。雷达高程为500 m,机载电子战设备高程为8 000 m,雷达载频为3 000 MHz,屏障1距雷达20 km,屏障高程为700 m,屏障2距雷达50 km,屏障高程为700/1 400 m,电磁波传输损耗随距离的变化情况如图8和图9所示。

图8 屏障1为主峰时电磁波传输损耗情况Fig.8 Electromagnetic wave transmission loss situation when Barrier 1 is the main peak

图9 屏障2为主峰时电磁波传输损耗情况Fig.9 Electromagnetic wave transmission loss situation when Barrier 2 is the main peak

仿真结果表明,当屏障2高度为700 m时,对于雷达屏障1为主峰,由山峰遮蔽造成的电磁波绕射效应以屏障1为主,直至次峰屏障2对主峰屏障1与机载电子战设备之间的连线形成二次遮蔽,加剧了电磁波传输损耗;当屏障2高度为1 400 m时,对于雷达屏障2为主峰,次峰屏障1对主峰屏障2与雷达之间的连线未形成二次遮蔽,因此电磁波绕射效应与单独只有屏障2的曲线相同。

2.3 试验数据验证

采用搭载电子侦察设备的某商用试验机对地面临时辐射源进行远距离侦收,地面辐射源X频段,飞机距辐射源150～300 km,飞行高度为7 900 m,沿径向航线远离辐射源。

地面临时辐射源架设高程1 300 m,试验机与辐射源之间,在距离辐射源10 km处和20 km处分别有高程为1 350 m和1 400 m的两个屏障,如图10所示。试验机侦收到该辐射源的信号幅度在260 km后开始陡降,直至285 km后无法侦收。利用本文多峰绕射模型所构建的算法,按同样的参数进行仿真计算,在150～272.8 km距离区间内,仿真结果与试验数据在形成遮蔽的距离、遮蔽后电磁衰减曲线上均吻合;在272.8～285.0 km距离区间内,试验机转弯,切换了接收天线象限,导致电磁衰减曲线略有偏离(5 dB),如图11所示。

图10 辐射源近处屏障位置Fig.10 Barrier position near radiation source

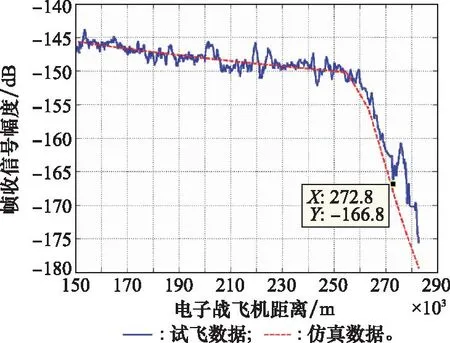
图11 试验数据与仿真结果的对比情况Fig.11 Comparison between experimental data and simulation results

试验与仿真结果对比表明,该算法可适用于计算地形遮蔽对机载电子战设备的影响。

3 机载电子战应对地形遮蔽下电磁绕射效应的策略

3.1 机载电子战突防高度的选择

现代战争中,突防电子战飞机为躲避对方地面雷达的探测与打击,往往采取低空、超低空突防的策略[34]。然而,深入纵深的超低空突防机常有被单兵肩抗式导弹击落的记录。

本文依据前文电磁波绕射效应模型,给出了地形遮蔽条件下雷达对不同距离、不同高度层突防飞机探测能力的影响,提供了突防编队在躲避地面雷达探测条件下尽可能拉高突防高程、规避低空肩抗式导弹攻击的路径规划思路。

假设对方雷达可在距离R0处刚好探测到雷达散射截面(radar cross section, RCS)为σ0的目标,根据雷达方程,该雷达接收灵敏度为

(10)

式中:Gt为雷达发射天线增益;Gr为雷达接收天线增益;Pt为雷达发射功率;λ为探测雷达波长。

对于RCS为σ的突防机,若希望借助地形遮挡获得的电波传输损耗,将雷达探测距离压缩到R,则由地形遮蔽引入的空间电磁波传输损耗A(计入雷达收发双程损耗)应为

将式(10)代入式(11),化简后可得

以在R0=300 km可探测到RCS=0.1 m2目标的雷达为对象进行仿真建模,电子战突防机RCS=10 m2,雷达高程500 m,屏障距雷达20 km,高程1 000 m,飞机在不同距离上满足不被雷达发现的最大高程如图12所示。

图12 突防机在不同距离可不被雷达探测的最大高程(屏障距雷达20 km,高程1 000 m)Fig.12 When the barrier is 20 km away from the radar, with an elevation of 1 000 m, the maximum elevation at which aircraft cannot be detected from different distances

雷达高程500 m,屏障距雷达50 km,高程1 500 m,其他条件不变,飞机在不同距离上满足不被雷达发现的最大高程如图13所示。

图13 突防机在不同距离可不被雷达探测的最大高程(屏障距雷达50 km,高程1 500 m)Fig.13 When the barrier is 50 km away from the radar, with an elevation of 1 500 m, the maximum elevation at which aircraft cannot be detected from different distances

3.2 地形遮蔽下远距离支援干扰阵位选择

机载电子战设备执行远距离支援干扰任务时,受地形遮蔽的影响,支援干扰效能会下降。本文依据电磁波绕射效应模型,从干扰功率维度给出了地形遮蔽条件下支援干扰掩护距离与机载电子战设备阵位选择之间的关系。

假定机载电子战设备可在距离对方雷达Rj0外(通视条件,无地形遮蔽)下将RCS为σ的突防机掩护至距雷达Rt0处,此时到雷达接收口面的干信比[35]为

(11)

式中:Gj为机载电子战设备发射天线增益;Pj为雷达发射功率;rj为干扰信号极化损耗。引入地形遮蔽电磁衰减Aj后,机载电子战设备在Rj的距离上可将突防机按照同样的JSR条件进行掩护,最大可掩护距离变为

(12)

将式(12)代入式(11),化简式(12),可得

(13)

对在Rj0=300 km将目标掩护至Rt0=50 km处的机载电子战设备进行建模分析,雷达高程500 m,屏障距雷达20 km,屏障高程700 m,机载电子战设备在不同高度层、不同距离上实施支援干扰,有效掩护距离如图14和图15所示。

图14 地形遮蔽下机载电子战设备在不同高程上对突防机的掩护效果(屏障距雷达20 km)Fig.14 With a barrier of 20 km away from the radar, the cover effect of airborne electronic warfare equipment with different elevations

图15 地形遮蔽下机载电子战设备在不同高程上对突防机的掩护效果(屏障距雷达50 km)Fig.15 With a barrier of 50 km away from the radar, the cover effect of airborne electronic warfare equipment with different elevations

上述条件下的仿真结果表明,机载电子战设备高度为8 000 m,若屏障距雷达20 km,将突防机掩护至距雷达100 km处,机载电子战设备距离需在267 km以内;若屏障距雷达50 km,将突防机掩护至距雷达100 km处,机载电子战设备距离需在312.5 km以内。

4 结 论

机载电子战设备与雷达在地形遮蔽非通视条件下,通过电磁波绕射效应,仍可衍生出诸多对抗策略。本文依据地球曲率修正了传统刃形单峰绕射模型,提出了基于Picquenard刃形多峰绕射模型的迭代主峰搜索算法;基于上述模型仿真了机载电子战设备与雷达之间不同距离、不同高程障碍物下的电磁绕射效应,并通过实际试验数据进行了验证。最后,给出了突防飞机如何利用地形遮蔽条件实现最大高程突防的边界条件;提供了执行远距离支援干扰任务的机载电子战设备如何利用地形遮蔽情况选择作战阵位的思考及仿真分析,能够为机载电子战作战部署提供决策参考。