计数原理单元测试卷（A卷）答案与提示

一、单选题

1.B 提示:从4名男生与3名女生中选2人,其中男女各1 人,由分步计数原理可得,不同的选派方法数为4×3=12。

2.A 提示:先将不相邻的两队排除,将贵阳折耳根队与柳州螺蛳粉队看成一个整体,与余下两队排列,有A33种方法,再将不相邻的两队插入它们的空隙中,有A24种方法,最后贵阳折耳根队与柳州螺蛳粉队之间的排法有A22种,故不同的站法有A33A24A22=144(种)。

3.A 提示:由组合数性质知,C7n+C8n=,故

解得n=14。

4.D 提示:(解法一)用间接方法,从这7个点中任选2 个点作直线,一共有C27条,其中从共线的B,D,E,F的4个点中任选2个点,可得C24条直线。因此,所得直线的条数为

(解法二)用直接方法,①过点B,D,E,F的直线只有1条;

②过A,C,G中的任意2 个点作直线,可作3条直线;

③从B,D,E,F中任取1 个点,从A,C,G中任取1个点作直线,可作直线条数为4×3=12。

综上,所得直线的条数为1+3+12=16。

5.C 提示:梯形的上、下底平行且不相等,如图1所示。

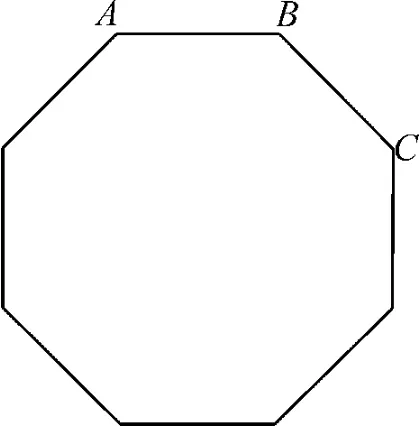
图1

若以AB为底边,则可构成2个梯形,根据对称性可知此类梯形有2×8=16(个)。

若以AC为底边,则可构成1个梯形,此类梯形共有1×8=8(个)。

所以梯形总共的个数是16+8=24。

则含x2的项的系数为1·C26(-1)2-1·C36(-1)3=35。

7.C 提示:先将5个人分为3组, 每组的人数分别为3、1、1或2、2、1。

若3组的人数分别为3、1、1,则教师夫妇必在3 人的一组,则教师夫妇这组还需从剩余的3人中抽1人,此时不同的分组方法数为

若3组人数分别为2、2、1,则2人一组中有一组是教师夫妇,只需将剩余3 人分为2组,且这2组的人数分别为2、1,此时不同的分组方法数为

接下来,将所分的3 组分配给3 所不同的学校,不同的安排方案种数为(3+3)A33=6×6=36。

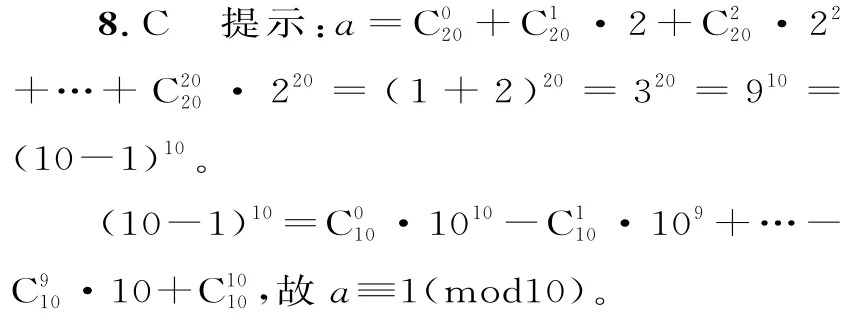
依次验证选项知2 021≡1(mod10)。

二、多选题

9.BCD 提示:对于选项A,Amn=n×(n-1)×(n-2)×…×(n-m+1),故A1020=20×19×18×…×11,A 错误。

对于选项D,甲、乙、丙3 名教师需分配一个班级,才能达到最优化教学效果。

故剩余5名教师可按1,2,2和1,1,3两种情况分类,有种分配方法,故D 正确。

12.AC 提示:由题中图知,从A地出发到B地的最短路径包含7步,其中3步向上,4步向右,且前3步中至少有1步向上,则不同的路径共有C13C24+C23C14+C33=31(条),故A 正确、B错误。

若甲途经C地,则不同的路径共有=18(条),故C正确。

若甲途经C地,且不经过D地,则不同的路径共有C13C13=9(条),故D 错误。

三、填空题

13.41 提示:a9=C99(-1)9+mC=10m-1,a10=m。

因为a9=a10,所以10m-1=m,解得m

14.2 提示:(1-ax+x2)4=[1+(x2-ax)]4,所以[1+(x2-ax)]4的展开式的通项为:

展开式共有9项,当r=0,4,8 时,展开式为有理项。

把展开式中所有的项重新排成一列,有理项都互不相邻,即把其他的6 个无理项先任意排,再把这3个有理项插入形成的7 个空隙中,方法共有A66·A37种方法。

故有理项都互不相邻的概率P=

16.12 提示:①当a=0时,b取集合内任一实数均有实数解,此时有4对。

②当a≠0时,一元二次方程有解则满足Δ=4-4ab≥0,即ab≤1。

当a=-1时,b可取的值有-1、0、2、3;

当a=2时,b可取的值有-1、0;

当a=3时,b可取的值有-1、0。

共有12个实数对满足题意。

四、解答题

17.(1)先将4名女生排在一起,有A44种排法;

甲、乙相邻,他们之间有A22种排法。

最后将排好的甲、乙这个整体与丙分别插入原先排好的4人形成的5个空隙中,有种排法。

化简整理得n2-3n-54=0。而n≥6,解得n=9。

所以n=9。

19.(1)由1＜log2x＜3,得log22＜log2x＜log223,故2＜x＜8。所以A={3,4,5,6,7},A∪B={3,4,5,6,7,8}。

从A∪B中取出3个不同的元素组成三位数,可以组成A36=120(个)三位数。

(2)由(1)得A={3,4,5,6,7},而且B={4,5,6,7,8}。

若从集合A中取元素3,则3不能作千位上的数字,有C35·C13·A33=180(个)满足题意的正整数。

若不从集合A中取元素3,则有=384(个)满足题意的正整数。

所以,满足题意的正整数的个数为180+384=564。

解得n=6或n=-7(舍去)。

因为所有项的系数之和为1,所以(a-1)6=1,解得a=0(舍去)或a=2。

(2)展开式中存在常数项。

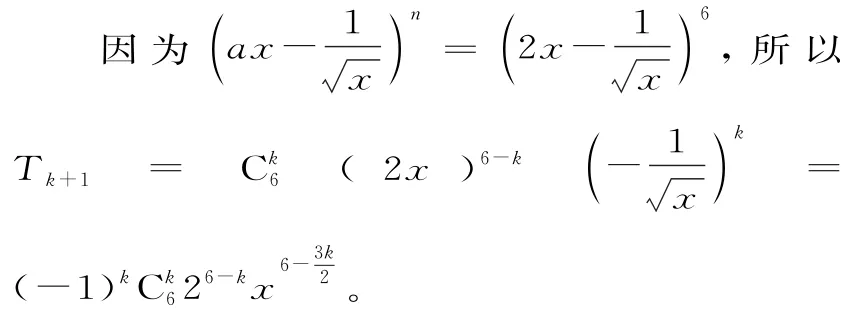
所以展开式中常数项为T5=(-1)4C4622x0=60。

21.(1)要组成无重复数字的四位偶数,则个位数字为2、4、6其中一个即可,可以组成C13·A35=180(个)四位偶数。

(2)要组成数字1、3、5 互不相邻的六位数,先将2、4、6排列好,再将1、3、5插入到排列所形成的空隙中,则可以组成A33·A34=144(个)数字1、3、5互不相邻的六位数。

(3)将六位数的数字从左到右分别记作第一位、第二位、…。

将6、4分别安排在第一位和第二位,则有C14A33=24(个)。

将6、4分别安排在第一位和第五位,则有A33=6(个)。

将6、4分别安排在第三位和第四位,则有C12A33=12(个)。

将6、4分别安排在第三位和第五位,则有A33=6(个)。

综上,共有24+18+12+6+18+12+6+12+6+6=120(个)满足题意的六位数。

22.(1)(a-2x)8的二项展开式的通项为Tr+1= Cr8a8-r· (- 2x)r=(-2)ra8-rCr8xr。

令r=2,得(-2)2a8-2C28=81 648。

又a＞0,故a3=27,a=3。

(2)(ⅰ)由(1)得(3-2x)8=a0+a1(x-1)+a2(x-1)2+…+a8(x-1)8。

令x=2,得a0+a1+a2+…+a8=(3-2×2)8=1。①

令x=0,得a0-a1+a2-…-a7+a8=38。②

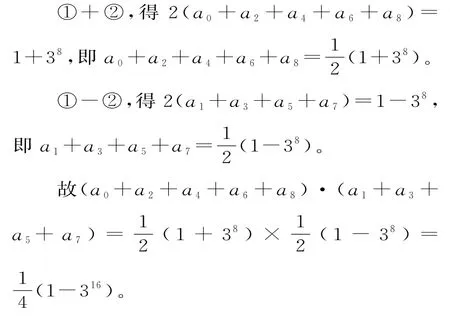
(ⅱ)令x-1=t,则x=t+1。

[3-2(t+1)]8=(1-2t)8=a0+a1t+a2t2+…+a8t8。

(1-2t)8的二项展开式的通项为Tk+1

故a0,a2,a4,a6,a8为正数,a1,a3,a5,a7为负数。

因此,|a0|+|a1|+|a2|+…+|a8|=a0-a1+a2-…+a8=38。