递推思想在排列组合中的应用

■河北南宫中学 韩文娟 霍忠林

利用递推思想求解排列组合问题是一种解题思路,但对同学们的数学素养要求较高,是排列组合中的难点。如何借助分类加法计数原理和分步乘法计数原理找到递推关系这是解题的关键点,下面通过六种题型来分析递推思想在排列组合中的应用。

题型一、爬楼梯问题

例1一段楼梯,有10个台阶,小明每次走一个或两个台阶,则他有多少种不同的走法?

解析:问题一般化:一段楼梯,有n个台阶,小明每次走一个或两个台阶,则他有多少种不同的走法?

设小明走n个台阶有an种走法,则a1=1,a2=2。

思路一 按第一步走的台阶数分类

若第一步走一个台阶,则余下的n-1个台阶共有an-1种走法。

若第一步走两个台阶,则余下的n-2个台阶共有an-2种走法。

所以an=an-1+an-2(n≥3)。

当n=10时,易得a10=89。

思路二 按最后一步走的台阶数分类

若最后一步走一个台阶,则前n-1个台阶共有an-1种走法。

若最后一步走两个台阶,则前n-2个台阶共有an-2种走法。

所以an=an-1+an-2(n≥3)。

当n=10时,易得a10=89。

评析:“爬楼梯问题”本质上就是“斐波那契数列”,该数列是普通高中教材人教A 版《数学选择性必修第二册》第11页、第12页的内容。采用类似方法还可以处理下面变式。

变式1:一段楼梯,有5个台阶,小明每次走一个或两个或三个台阶,则他有多少种不同的走法?

解析:该问题等价于:已知数列an=an-1+an-2+an-3(n≥4),其中a1=1,a2=2,a3=4,求a5的值。过程略。

题型二、平面划分问题

例23 条直线最多能将平面分成几部分?4条直线最多能将平面分成几部分呢?

解析:问题一般化:n条直线最多能将平面分成几部分?

设n条直线最多将平面分成an部分,则前n-1 条直线最多将平面分成an-1部分。要使第n条直线将平面分成的部分最多,则第n条直线必须与前n-1条直线均相交,此时共有n-1 个交点,增加n部分,从而有an=an-1+n(n≥2),其中a1=2。容易得到a3=7,a4=11,即为本题所求的答案。

评析:平面划分问题是典型的an=an-1+f(n)型递推公式的应用,通过累加法可以得到

题型三、错排问题

例3甲、乙、丙、丁、戊5 个人排成一排,重新站队,各人都不站在原来的位置,共有多少种不同的站队方式?

解析:问题一般化:n个人排成一排,重新站队,各人都不站在原来的位置,共有多少种不同的站队方式?

设n个人排成一排,重新站队,各人都不站在原来的位置共有an种方法。

第一步,第一个人不站在原来的位置共有n-1种方法。

第二步,不妨设第一个人站在第二个人的原来位置,则第二个人的站法又可以分为两类:

第一类是第二个人站在第一个人原来的位置,此时余下的n-2人共有an-2种站法;

第二类是第二个人不站在第一个人原来的位置,此时第三个人不站在第三个人原来的位置,第四个人不站在第四个人原来的位置,……,第n个人不站在第n个人原来的位置,所以有an-1种站法。

由分类加法计数原理和分步乘法计数原理得an=(n-1)·(an-1+an-2)(n≥3),其中a1=0,a2=1。

容易得到a5=44,即为本题所求的答案。

评析:错排问题的本质是先把n个不同元素排成一排,再重新排列,所有元素各有一个指定位置不能站,且不同元素不能站的指定位置也不同。上述解题过程中第二步的第二类:从第二个人到第n个人,每个人均有一个指定位置不能站,且不同的人不能站的指定位置也不同,因此是n-1个人的错排问题。比如例3与下面变式本质是一样的。

变式2:甲、乙、丙、丁、戊排成一排,重新站队时,甲不能站原来乙的位置,乙不能站原来丙的位置,丙不能站原来丁的位置,丁不能站原来戊的位置,戊不能站原来甲的位置,则不同的站队方式有多少种? (答案略。)

题型四、传球问题

例4甲、乙、丙三人传球,由甲开始发球,并作为第一次传球,经过5 次传球后,球仍回到甲手中,则不同的传球方式有多少种?

解析:问题一般化:甲、乙、丙三人传球,由甲开始发球,并作为第一次传球,经过n次传球后,球仍回到甲手中,则不同的传球方式有多少种?

设n次传球后,球仍回到甲手中有an种方法,要使第n次传球后,球在甲手中,则第n-1次传球后球一定在乙或丙手中,而n-1次传球一共有2n-1种方法,所以第n-1次传球后球在乙或丙手中的种类数为2n-1-an-1。

接着乙或丙再向甲传最后一次球,所以an=2n-1-an-1(n≥2),其中a1=0。

容易得到a5=10,即为本题所求的答案。

评析:传球问题是排列组合中最经典的问题。实际上例4还可以推广为“m(m≥2)个人传球,由甲开始发球,并作为第一次传球,经过n(n≥2)次传球后,球仍回到甲手中,则递推关系为an=(m-1)n-1-an-1(m≥2,n≥2),其中a1=0”。

题型五、环形区域染色问题

例5用4 种不同颜色给六边形A1A2A3A4A5A6的6个顶点染色,每个顶点染一种颜色,相邻的顶点染不同的颜色,则有多少种不同的染色方法?

解析:问题一般化:用m种不同颜色给n边形A1A2…An的n个顶点染色(其中m≥3,n≥3),每个顶点染一种颜色,相邻的顶点染不同的颜色,则有多少种不同的染色方法?

设用m种不同颜色给n边形A1A2…An的n个顶点染色(其中m≥3,n≥3),每个顶点染一种颜色,相邻的顶点染不同的颜色的染色方法有an种,现在从A1到An依次染色。

第一步,染A1共有m种方法。

第二步,染A2共有m-1种方法,同理染A3,…,An均有m-1种方法,根据分步乘法计数原理得共有m(m-1)n-1种方法,但是要去掉A1与An同色的种类数。当A1与An同色时,此时可将A1与An合并看成一个点,则此时有an-1种方法,故an=m(m-1)n-1-an-1(其中m≥3,n≥3),其中a3=A3m。

容易得到当m=4,n=6时a6=732,即为本题所求的答案。

评析:环形区域染色问题与传球问题的求解思路类似,不同点是传球问题第一个发球者是固定的,而环形区域染色问题第一个染色点不固定。若将例4 改为“甲、乙、丙三人传球,第一次发球者传给其他任意一人,第二次由拿球者再传给其他任意一人,经过5次传球后,球仍回到最初发球者手中,则不同的传球方式有多少种”,这样就是环形区域染色问题。

题型六、结草成环问题

例6现有3根草,共有6 个草头,现将6个草头平均分成3组,每两个草头打结,则打结后所有草构成一个圆环的打结方法有多少种?

解析:问题一般化:现有n根草,共有2n个草头,现将2n个草头平均分成n组,每两个草头打结,则打结后所有草构成一个圆环的打结方法有多少种?

设n根草构成一个圆环的打结方法共有an种,现将草头如图1 编号为1,2,3,…,2n-1,2n。

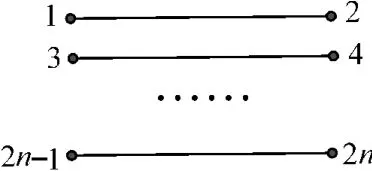
图1

草头1可以与草头3,4,…,2n-1,2n打结,共2n-2种方法;不妨设草头1与草头3打结,此时可将问题转化为“n-1 根草打结后所有草构成一个圆环的问题”,故共有an-1种方法,根据分步乘法计数原理得an=(2n-2)·an-1(n≥2),其中a1=1。

容易得到a3=8,即为本题所求的答案。

评析:结草成环问题是一个古老的游戏问题,是典型的an=f(n)·an-1型递推公式的应用,通过累乘法可以得到an=2n-1(n-1)!。

通过对上述六种题型的研究可以发现,有些排列组合问题通过合理分步、恰当分类,巧妙地运用递推数列的思想方法,不仅可以化繁为简,轻松破解,还能将问题拓展和推广,从而达到“做一题、会一类、通一片”的效果。