涂色问题的解题技巧
2024-03-26江苏省张家港中等专业学校韩文美
■江苏省张家港中等专业学校 张 娴 韩文美
排列组合中有一类常见问题——涂色问题,此类问题基于两个计数原理与排列组合知识,关注图形的结构特征,解决方法技巧性强且灵活多变,有利于培养同学们的创新思维能力、分析问题与观察问题以及解决问题的能力,已成为数学命题中比较常见的一类基本题型,备受各方关注。
1.直线型涂色问题
例1(2022—2023学年江苏省常州一中高二下学期段考数学试卷)现有6种不同的颜色,给图1 中的5 个格子涂色,每个格子涂一种颜色,要求最多使用4种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有_____种。

图1
分析:根据题设条件,选出的颜色可以是2种,3种或者4种,依次通过直线型的图形结构特征求出方法数,通过分类法求和,即可得以分析与求解。
解:由题意选出的颜色可以是2种,3种或者4种,规定左边起为第一个空,不同情况如下。
当选出2种颜色时,第一个空有2 种选择,第一个空颜色确定后,其余空颜色就确定了,共有C26×2=30(种)方法。
当选出3种颜色时,第一个空有3 种选择,第二个空有2种选择,第三个空可分为与第一个空颜色相同和不同的情况,第四个空和第五个空都各有2 种选择,但要去掉整体只用了2 种颜色的情况,共有C36C13C12·=840(种)方法。
当选出4种颜色时,必有2种颜色相同,可采用插空法,将这2 种相同颜色去插入另外3种颜色形成的空,共有(种)方法。
综上分析,不同的涂色方法共有30+840+2 160=3 030(种)。
点评:直线型涂色问题往往从第一个位置入手,逐一分析,在前一个已涂色的条件下涂下一个位置,注意对不同位置的分析加以合理分类讨论与分步处理,进而确定直线型涂色问题的种数。
2.区域型涂色问题
例2(2022—2023学年湖北省武汉市高二下学期期中数学试卷)七巧板是古代劳动人民智慧的结晶。图2是某同学用木板制作的七巧板,它包括5个等腰直角三角形、一个正方形和一个平行四边形。若用四种颜色给各板块涂色,要求正方形板块单独一色,其余板块两块一种颜色,而且有公共边的板块不同色,则不同的涂色方案有____种。
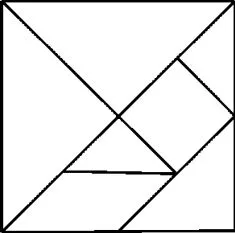
图2
分析:根据题设条件,先对七巧板中的不同区域加以合理标记,并通过画图分析其中四板块A,B,C,D必涂上不同颜色,再根据分类、分步计数原理计算剩下的部分即可得以分析与求解。
解:由题意知,对七巧板中的不同区域加以合理标记,如图3所示。

图3
由于一共4种颜色,板块A需单独一色,剩下6个板块中每2个区域涂同一种颜色,且板块B,C,D两两有公共边不能同色,故板块A,B,C,D必定涂不同的颜色。
①当板块E与板块C同色时,则板块F,G与板块B,D或板块D,B分别同色,共有2种情况。
②当板块E与板块B同色时,则板块F只能与D同色,板块G只能与C同色,共1种情况。
又板块A,B,C,D颜色可排列,故共(2+1)×=72(种)方案。
点评:区域型涂色问题,应该给区域依次标上相应的序号,以便分析问题。在给各区域涂色时,要注意不同的涂色顺序,其解题就有繁简之分。在实际解答时,应按不同的涂色顺序多多尝试,看哪一种最简单。
3.立体型涂色问题
例3(2024 届上海市七宝中学高三上学期期中数学试卷)某数学兴趣小组用纸板制作正方体教具,如图4 所示,现给图中的正方体展开图的6个区域涂色,有红、橙、黄、绿4种颜色可选,要求制作出的正方体相邻面所涂颜色均不同,共有_____种不同的涂色方法。
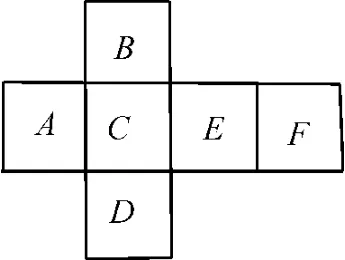
图4
分析:根据题设条件,由正方体展开图的平面图形回归正方体的立体图形,先从涂A入手,再分C与F同 色、C与F不 同 色 两 种情况讨论,利用分步、分类计数原理分析与运算可得答案。
解:如图5 所示,还原回正方体后,D、B为正方体的前后两个对面,A、E为正方体的左右两个对面,F、C为正方体的上下两个对面,先涂A有4种涂法。①当C与F同色时,涂C有3种涂法,若D与B同色,则有2种涂法,最后涂E有2种涂法;若D与B不同色,则有种涂法,最后涂E有1种涂法。
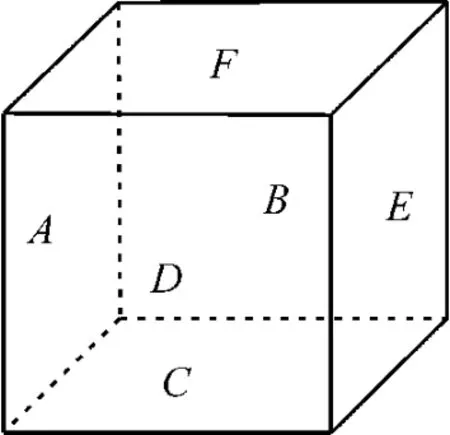
图5
②当C与F不 同 色 时,涂C有3 种 涂法,涂F有2种涂法,此时D与B必同色且只有1种涂法,E也只有1种涂法。
则有4×3×2×1×1=24(种)涂法。
综上分析可得,一共有72+24=96(种)不同的涂法。
点评:立体型涂色问题,往往要同时考虑平面几何的结构特征,又要考虑立体几何的结构特征,综合“二维”与“三维”中的涂色要求与限制条件,全面考查同学们的空间想象能力与逻辑推理能力。
4.环状型涂色问题
例4(2024届浙江省名校联盟高三上学期9 月份月考数学试卷)五行是华夏民族创造的哲学思想,多用于哲学、中医学和占卜方面。五行学说是华夏文明重要的组成部分。古代先民认为,天下万物皆由五类元素组成,分别是金、木、水、火、土,彼此之间存在相生相克的关系。图6 是五行图,现有5种颜色可供选择给五“行”涂色,要求五行相生不能用同一种颜色(例如金生火,水生木,不能同色),五行相克可以用同一种颜色(例如水克火,木克土,可以用同一种颜色),则不同的涂色方法种数为( )。

图6
A.3 125 B.1 000
C.1 040 D.1 020
分析:根据题设条件,从数学文化场景中加以合理转化,抽象问题的本质与内涵,通过环状型涂色问题来转化,并加以分析,先根据不相邻区域是否同色进行分类,确定涂色顺序,再分步计数即可。
解:依题可知五行相克可以用同一种颜色,也可以不用同一种颜色,即无限制条件而五行相生不能用同一种颜色,即相邻位置不能用同一种颜色。
故问题转化为图7中A,B,C,D,E5个区域,有5种不同的颜色可用,要求相邻区域不能涂同一种颜色,即5种颜色5个区域的环状涂色问题。
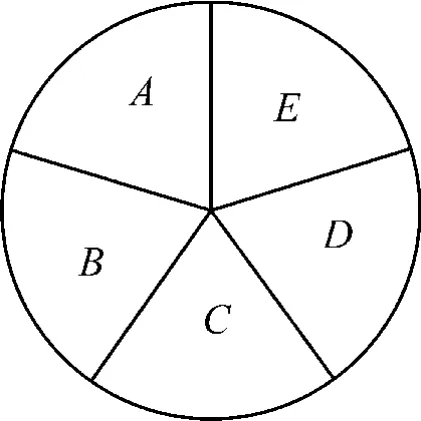
图7
分为以下两类情况。
第一类,A,C,D3个区域涂3种不同的颜色。
第一步涂A,C,D区域,从5 种不同的颜色中选3 种按顺序涂在不同的3 个区域上,则有A35种方法;
第二步涂B区域,由于A,C颜色不同,则有3种方法;
第三步涂E区域,由于A,D颜色不同,则有3种方法。
由分步计数原理知,共有3×3×A35=540(种)方法。
第二类,A,C,D3个区域涂2种不同的颜色。
C,D不能涂同种颜色,则A,C涂色相同,或A,D涂色相同,两种情况方法数相同。
若A,C涂色相同,第一步涂A,C,D区域,A,C可看成同一区域,且A,D区域不同色,即涂2个区域不同色,从5种不同的颜色中选2种按顺序涂在不同的2个区域上,则有A25种方法;
第二步涂B区域,由于A,C颜色相同,则有4种方法;
第三步涂E区域,由于A,D颜色不同,则有3种方法。
由分步计数原理知,共有4×3×A25=240(种)方法。
若A,D涂一色,与A,C涂一色的方法数相同,则共有2×240=480(种)方法。
由分类计数原理可知,不同的涂色方法数为540+480=1 020。选D。
点评:求解环状型涂色问题,是基于直线型涂色问题加以分析与处理,同时要考虑最后一个位置与原来第一个位置之间的限制,这样才能形成一个闭环,这也是解决问题中比较容易出错的一个环节,要加以高度重视。
5.探究型涂色问题
例5(2023 年吉林省长春市高考数学质检试卷)将圆分成n(n≥2,且n∈N*)个扇形,每个扇形用红、黄、蓝、橙四色之一涂色,要求相邻扇形不同色,设这n个扇形的涂色方法为an种,则an与an-1的递推关系是____。
分析:根据题设条件,对n个扇形依次加以编号,按n=2与n>2两种情况加以分类讨论an的情况,由分步计数原理得到an与an-1之间的关系。
解:将圆分成n个扇形时,将n个扇形依次设为T1,T2,…,Tn。
设这n个扇形的涂色方法为an种。
当n=2时,a2=4×3=12。
当n>2 时,T1有4 种 涂 法,T2有3 种涂法,接着T3,T4,…,Tn-1,Tn,依次有3种涂法,故共有4×3n-1种涂法。
但当Tn与T1的颜色相同时,有an-1种涂法,an=4×3n-1-an-1。
点评:求解探究型涂色问题,往往从最简单的图形入手,依次分析两个图形涂色之间的联系与差别,进而加以合理推理,构建相应的关系式,得以解决对应的探究性问题,从而实现问题的解决。
对于涂色问题,抓住探究问题的本质,结合涂色图形的结构特征,以及涂色的种数与限制条件,从关键点入手,结合选取颜色加以分析,合理分类讨论,借助两个计数原理以及排列组合知识,注意“重”或者“漏”的情形,进而加以合理操作与计算。
