利用二级结论 优解椭圆小题——2023年高考数学甲卷理科第12题解法探究

■甘肃省张掖市实验中学 王新宏

圆锥曲线试题是高考数学的必考试题,是重点也是难点。大部分同学对其有畏惧心理,找不到解决的突破口。2023年高考数学甲卷理科第12题是一道椭圆压轴小题,它以椭圆焦点三角形为背景,考查椭圆的定义、余弦定理、焦点三角形等知识,题干简洁,设问直接,内涵丰富。本题入手比较容易,方法比较多,考查同学们理性思维与数学探究能力,体现了逻辑推理、直观想象、数学运算等核心素养。解决本题的关键在于数形结合,即可考虑用余弦定理,也可考虑焦半径公式、焦点三角形面积公式、中线的向量公式、中线定理、极化恒等式等相关二级结论迅速求解。试题凝聚了命题专家的心血与智慧,简约而不简单,为不同能力水平的同学提供了相应的思考空间,是一道独具匠心的好题。

1.试题呈现

2023年高考数学甲卷理科第12题:

如图1 所示,设O为坐标原点,F1,F2为椭圆C=1 的两个焦点,点P在 椭 圆C上,cos ∠F1PF2=,则|OP|=( )。

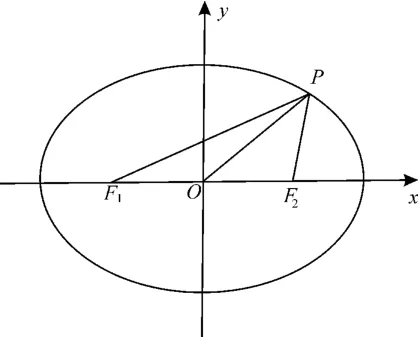
图1

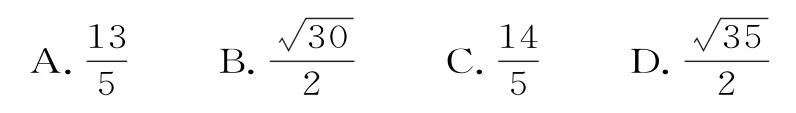
2.解法探究

解法1:(挖出两角互补这个隐含条件)

由椭圆方程知a2=9,b2=6。

因为c2=a2-b2,所以a=3,c= 3,e=

在△PF1F2中,由余弦定理得:

点评:解题的关键是发现∠POF1+∠POF2=π,cos ∠POF1=-cos ∠POF2这样的隐含条件,它往往能帮助整个题目的顺利求解。

解法2:(借焦半径之力)

解法3:(与焦点三角形面积公式结合)

证明过程:如图2 所示,设P(x,y),由余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cosα。①

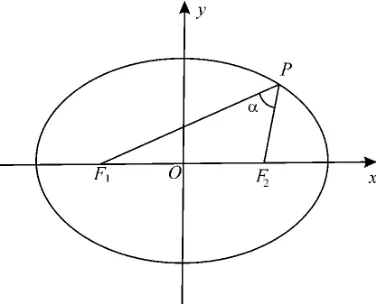
图2

由椭圆的定义得:

|PF1|+|PF2|=2a。②

则 ②2- ① 得:|PF1|· |PF2| =

解法4:(与中线的向量公式结合)

点评:如图3所 示,若AD为△ABC边BC的中 线,则,中线的向量公式在高考中也备受青睐。

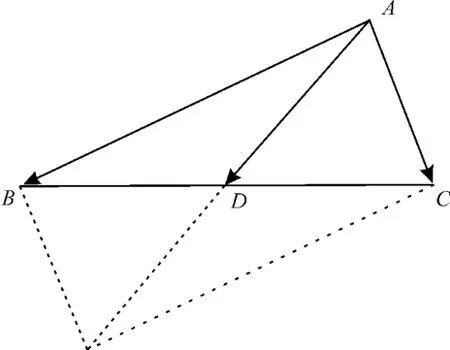
图3

图4

解法5:(与中线定理结合)

由题意知|PF1|+|PF2|=2a=6。①

|PF1|2+|PF2|2-2|PF1||PF2|·cos∠F1PF2= |F1F2|2,即|PF1|2+

联立①②,解得|PF1|2+|PF2|2=21。

解法6:(与极化恒等式结合)

极化恒等式在处理与中线有关的数量积时,往往会出奇制胜,事半功倍。

3.巩固练习

(2)(2019年全国Ⅰ卷文科第12题)已知椭圆C的焦点为F1(-1,0),F2(1,0),过F2的直线与椭圆C交于A,B两点,如果|AF2|=2|F2B|,|AB|=|BF1|,则椭圆C的方程为( )。

4.小结与启示

从以上内容可以看出,对于解析几何小题,一般不直接考虑设点的坐标运算,而是先画草图,接着充分考虑图形的几何性质特征与圆锥曲线定义,以及相关的二级结论,这样往往更能帮助同学们看清图形元素间内在的联系,挖掘问题本质,简化解题过程,减少运算量,提高解题的效率,快速准确解题。

对高考真题进行适当的研究,不但可以明确高考重难点,把握高考方向,避免学习的随意性、盲目性,而且可以有效训练同学们的思维能力,培养创新意识,提高学习数学的兴趣。