基于改进虚拟同步发电机控制的功率交互振荡抑制策略

2024-03-26贾焦心秦本双颜湘武陈一丹杨添淇

电力自动化设备 2024年3期

贾焦心，秦本双，颜湘武，陈一丹，杨添淇

（1.华北电力大学分布式储能与微网河北省重点实验室，河北保定 071003；2.河南理工大学电气工程与自动化学院，河南焦作 454003；3.河南省煤矿装备智能检测与控制重点实验室，河南焦作 454003；4.国网上海浦东供电公司，上海 200122）

0 引言

为实现“双碳”目标［1-3］，大规模开发和利用可再生能源是一种重要的技术手段。随着高渗透率新能源的并网，电力系统逐渐呈现“双高”特点［4-5］。新能源发电主要通过并网逆变器接入电网，因此，并网逆变器控制对“双高”电网具有重要作用，这就需要并网逆变器具备组网能力和惯性支撑能力［6］。

虚拟同步发电机（virtual synchronous generator，VSG）技术［7-8］因满足电网“双高”特点对并网逆变器的需求而得到了快速发展［9-10］。与同步发电机（synchronous generator，SG）相比，VSG 的参数设计相对灵活，VSG 不仅能够从外特性上完全模拟SG，而且能够实现比SG 更宽的运行范围和更快的动态响应速度［11］。然而，虚拟惯量的引入将VSG 有功功率-频率控制环路的一阶特性转化为二阶振荡特性。在指令功率发生扰动时，由于电网阻抗的存在，VSG控制环路间会产生交互作用，易引发功率间的交互振荡。

目前，许多学者已对VSG 接入电网引起的振荡问题开展了研究。文献［12］建立3 台VSG 并网系统的状态空间模型，基于特征值分析法研究不同系统参数变化对系统低频特征根的影响。文献［13］通过构建VSG 的宽频域动态耦合模型分析功率的同步频率谐振特性，并提出采用有源阻尼控制抑制功率振荡。文献［14］通过在控制算法中增加虚拟阻尼和虚拟阻抗抑制并联系统孤岛运行的功率低频振荡。文献［15］提出基于分布式通信架构的互阻尼控制策略，通过相邻VSG 间的互阻尼控制抑制孤岛运行时的功率振荡，但没有考虑弱电网工况下的振荡特性。文献［16-17］构建多VSG 并网系统的机械导纳模型，揭示多机系统的低频振荡机理，并研究不同参数变化时系统的振荡特性。在文献［16］的基础上，文献［18］提出通过引入虚拟阻抗抑制VSG 的低频振荡，但当虚拟阻抗取值过大时会引起有功、无功环路的耦合。文献［19］在构建多VSG 并网系统机械导纳模型的基础上，提出采用相对增益矩阵（relative gain array，RGA）原理定量分析VSG 控制环路角频率响应间的交互作用，但未对控制环路间交互作用的抑制方法进行研究。随着电力系统电力电子化程度的提高，构网型逆变器间的功率交互振荡特性愈加复杂，因此，有必要对VSG 控制环路功率间的交互振荡特性及振荡抑制策略进行研究。

本文首先在文献［19］的基础上，采用RGA 原理定量分析不同参数变化时VSG 有功功率间的交互作用；其次，基于RGA 原理的分析结果，提出采用转速阻尼功率高通反馈改进VSG 的有功功率-频率控制环路，对VSG 控制环路间的交互振荡进行抑制；然后，对比传统VSG 控制策略与改进VSG 控制策略的暂态性能和稳态性能，并进一步采用RGA 原理分析改进VSG 控制策略的交互振荡抑制效果；最后，通过仿真和实验验证所提改进VSG控制策略对VSG间交互振荡抑制的有效性。

1 VSG输出功率响应间的交互作用

1.1 VSG输出功率响应间交互作用研究的必要性

1）VSG输出功率响应间交互作用的理论分析。

采用的VSG 控制策略如图1所示。单台VSG 并网模式下的有功功率-频率环路小信号模型如图2所示。图中：eabc为VSG 输出电压瞬时值；irefabc为电感电流参考值；P、Q分别为VSG输出的电磁有功、无功功率；Pref、Qref分别为有功、无功功率参考值；kq为无功下垂系数；E0为VSG 电压参考值；E为VSG 输出电压；uabc为滤波电容电压；R为滤波电感的寄生电阻；L为滤波电感；θ为VSG 输出相角；ωs为VSG 参考角频率；ω为VSG输出角频率；DP为下垂系数；J为VSG虚拟惯量；iabc为电感电流；P̂ref为VSG 有功功率指令变化量；Ya( )s为VSG 的第一机械导纳；D为阻尼系数；ω̂为VSG 内禀角频率变化量；ω̂c为并网母线角频率变化量；Yb( )s为VSG的第二机械导纳；KP=EUPCC/Z为同步系数［16］，UPCC为公共耦合点处的电压初始值，Z为VSG 传输阻抗（输出阻抗与线路阻抗Zline之和）；δ̂为VSG相角变化量。

图1 VSG控制策略Fig.1 Control strategy of VSG

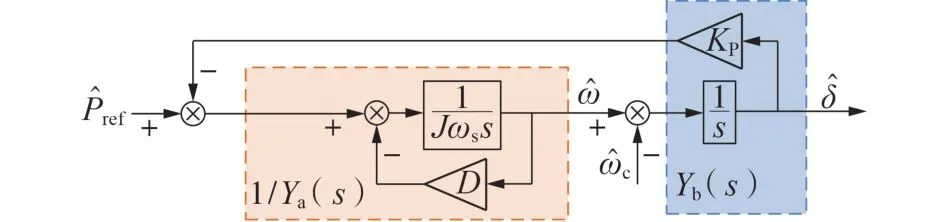
图2 单台VSG并网模式下的有功功率-频率环路小信号模型Fig.2 Small-signal model of active power-frequency loop under unit VSG grid-connection mode

针对图2 所示的VSG 有功功率-频率环路小信号模型，文献［16-17］利用机电比拟原理构建附录A图A1所示的单台VSG 机械导纳模型。Ya(s)和Yb(s)的表达式分别为：

在图A1单台VSG机械导纳模型的基础上，进一步计及电网阻抗的影响，可建立多台VSG 并网的机械导纳模型，如附录A 图A2所示。图中电网阻抗的机械导纳Yg( )s=Kg/s，同步系数Kg的计算方法与同步系数KP相同［19］。

根据图A2，基于叠加定理和基尔霍夫定律推导出VSG输出功率响应的具体表达式［16-17］，即：

式中：P̂m(s)为第m台VSG 输出有功功率的变化量；(s)为第m台VSG 有功功率指令变化量；n为并网VSG 的数量；ω̂g为电网角频率变化量；Ypm（s）为第m台VSG 的等效机械导纳；Mm(s)、Tm，l(s)、Sgm(s)、Ytemp(s)无物理含义。

由式（2）可知，VSG 的输出功率变化量由三部分组成：第一部分为VSG 自身有功功率指令输入扰动；第二部分为其他VSG 的交互作用；第三部分为电网频率扰动。

由上述推导可知，VSG 有功功率-频率控制环路功率响应间存在交互作用。

2）VSG输出功率响应间交互作用的仿真分析。

基于MATLAB／Simulink 仿真平台搭建4 台VSG（VSG1—VSG4）并联并网运行的仿真模型，如附录A 图A3 所示。仿真参数如附录B 表B1 所示。取电网电抗Xg=ωLg=0.157 Ω，其中Lg为电网电感。仿真工况如下：在0.2 s 时对VSG1的有功功率指令Pref1施加幅值为50 kW 的阶跃扰动。不同并网VSG数量下VSG1和VSG2的有功功率响应波形如附录A 图A4所示，图中Pi为第i台VSG的有功功率。

在有功功率指令Pref1的扰动下，当Lg=0.5 mH时，存在VSG 有功功率-频率控制间的交互作用大于扰动的情况，即图A4 中VSG2的有功功率响应超调量（n=2 时超调量为24.34 %，n=4 时超调量为21.42 %）大于VSG1的有功功率响应超调量（n=2 和n=4 时超调量均为11.8 %），这表明在某些参数下VSG控制环路间的交互作用可能影响系统的安全稳定运行。

由理论分析和仿真分析结果知，VSG 控制环路间的交互作用不可忽视，有必要对其进行定量分析。

1.2 VSG输出功率响应间交互作用的定量分析

RGA 原理是一种被广泛用于分析多输入多输出系统交互作用的有效方法，具有计算简单、可定量分析控制回路间交互作用强弱的优点［20］。文献［19］采用RGA 原理定量分析VSG 角频率响应间的交互作用，确定了角频率响应间的主要作用频率区间，但未对VSG 输出功率响应间的交互作用进行定量分析。本文将采用RGA 原理对VSG 输出功率间的交互作用进行定量分析，RGA 原理的分析流程参考文献［19］。基于RGA 原理计算出控制环路间的相对增益即可评定交互作用，相关标准参考文献［21］。文献［19］表明：并网VSG 数量n对角频率响应间交互作用的影响较小，虚拟惯量J、阻尼系数D及电网电感Lg对角频率响应间交互作用的影响较大，因此，本文主要研究参数J、D、Lg对VSG 输出功率响应间交互作用的影响。

为了验证RGA 分析结果的准确性，以传递函数Tm（s）的频域分析结果作为对比。VSG 的仿真参数如表B1 所示。参数J、D、Lg变化时VSG 有功功率间的交互影响分别如图3 及附录A 图A5、A6 所示。图中：λ11为VSG 有功环路间的相对增益值，为标幺值，后同；f为频率。

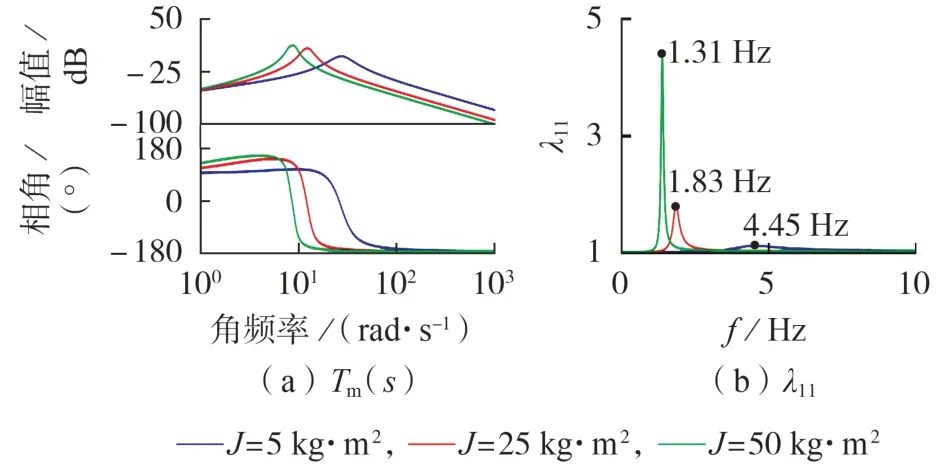
图3 J 变化时VSG有功功率间的交互影响Fig.3 Interaction between active powers of VSG when J changes

由图3 和图A6 可知：随着J和Lg的增大，VSG 控制环路间的负交互作用增大，且频率向低频方向移动；在所选择的参数下，与Lg增大时相比，J增大时频率向低频方向移动的速度更快。由图3可知，当J变化时，各相对增益曲线的谱峰均较尖，这表明J变化时控制环路间产生的负交互影响作用范围的频率区间较窄。由图A6 可知，当Lg变化时，各相对增益曲线的谱峰相对较宽，这表明Lg变化时控制环路间产生的负交互影响作用范围的频率区间较宽。由图A5 可知：当D增大时，VSG 控制环路间的耦合作用减小，且频率向高频方向移动；当D为60 N·m·s／rad或者90 N·m·s／rad 时，在所研究的频率区间内，控制环路间的相对增益λ11＜1.2 p.u.，这表明此时控制环路间的耦合作用较弱。

综上可以得出如下结论：不同参数变化时，VSG控制环路间的交互作用范围为1 Hz＜f＜8 Hz，其中，参数Lg变化时，控制环路间的交互作用范围最大且相对增益较大，这表明参数Lg对控制环路间的交互作用影响最大；当f＞8 Hz 时，VSG 控制环路间的相对增益λ11≠1 p.u.，这表明控制环路间存在交互作用，但由于λ11＜1.2 p.u.，交互作用较弱，因此可以忽略；增大D以及减小J和Lg有助于减小控制环路间的交互作用。

需要说明的是，与文献［19］相比，不同参数变化时VSG 输出功率间交互作用的变化规律与VSG 角频率响应间的变化趋势具有一致性，并且主要作用区间相同。通过对比发现两交互作用的区别在于：当f＞8 Hz 时，VSG 输出功率间的相对增益范围为1 p.u.＜λ11＜1.2 p.u.，而角频率间的相对增益λ11≈1 p.u.。虽然VSG 输出功率在f＞8 Hz 时仍然存在交互作用，但其影响较小，因此可以忽略。

2 控制策略对比

由1.2 节的分析可知，多台VSG 并网时存在有功功率间的交互作用，不利于系统的安全稳定运行，因此，本文提出抑制该交互作用的控制策略。

2.1 VSG控制策略

传统VSG 控制策略的有功功率-频率控制环路框图如图4（a）所示。由1.2 节的RGA 分析结果可知，增大D以及减小J和Lg有助于降低VSG 控制环路间的交互作用。由文献［22］可知，传统VSG 控制策略为典型的二阶系统，其高频段呈衰减特性。基于上述分析，本文提出采用转速阻尼功率高通反馈改进VSG有功功率-频率控制环路，增加VSG控制策略在低频段的阻尼，进而实现VSG 控制环路间交互作用的抑制，具体控制策略如图4（b）所示。图4中：TD为滤波器时间常数，其取值范围为（5～100）τ，τ=Jωs/D为时间常数；DH为高通阻尼系数，主要影响系统的动态性能，而对系统的稳态性能无影响，增大高通阻尼系数能够更好地抑制频率波动但调节过程的持续时间会增长。

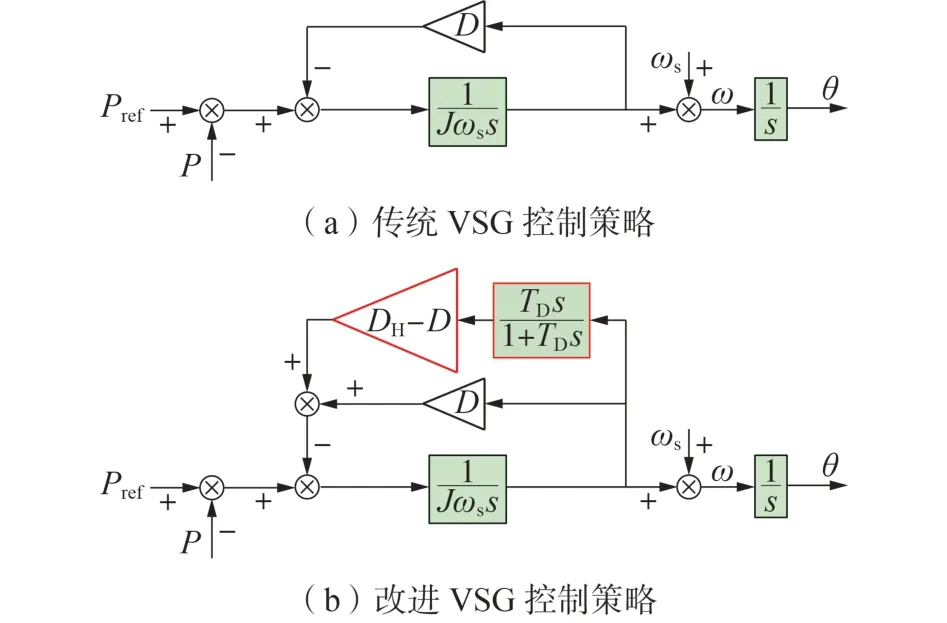
图4 VSG有功功率-频率控制框图Fig.4 Block diagram of active power-frequency control for VSG

基于图4 可写出传统VSG 控制策略和改进VSG控制策略的有功功率-频率环路的微分方程，分别如式（7）、（8）所示。

2.2 2种VSG控制策略的稳态性能对比

根据图4 所示的VSG 有功功率-频率控制环路框图，可构建传统VSG 控制策略及改进VSG 控制策略的统一小信号模型，如图5所示。

图5 VSG有功功率-频率环路小信号模型Fig.5 Small-signal model of active power-frequency loop for VSG

传统VSG 控制策略和改进VSG 控制策略有功功率到角频率的开环传递函数分别为G1( )s和G2(s)，即：

基于式（9）、（10），可得到2 种控制策略的稳态下垂方程，如式（11）所示。

式（11）表明，在VSG 的阻尼项中加入滤波环节会增大系统低频段阻尼，但不影响系统的稳态性能。

2.3 2种VSG控制策略的暂态特性对比

根据图5 所示的VSG 有功功率-频率小信号模型，可得到角频率扰动下VSG 输出功率响应的表达式，即：

式中：Yp1(s)为在角频率扰动下传统VSG控制策略输出功率响应的传递函数；Yp2( )s为在角频率扰动下改进VSG控制策略输出功率响应的传递函数。

由式（13）、（14）可知，传统VSG 控制策略的传递函数Yp1( )s是典型的二阶传递函数，而改进VSG控制策略的传递函数Yp2( )s是一个三阶的传递函数。为比较2种控制策略的暂态性能，对比2种控制策略输出功率响应传递函数的Bode 图，如附录A 图A7 所示。由图可知：2 种控制策略的高频衰减特性相同；2 种控制策略在中频段呈现的惯量阻尼特性不同，在1.4 Hz 处，传统VSG 控制策略产生幅值为1.05×106W 的谐振峰，而改进VSG 控制策略产生幅值为3.08×105W 的谐振峰，这表明改进VSG 控制策略增加系统阻尼，有助于抑制传统VSG 控制策略的低频振荡；在低频段，改进VSG 控制策略的增益略大于传统VSG 控制策略，但不影响系统的响应特性。

3 改进VSG控制的振荡抑制效果分析

为验证改进VSG 控制策略的振荡抑制效果，给出虚拟惯量J和电网电感Lg变化时采用改进VSG 控制策略的RGA 分析结果，分别如附录A 图A8、A9 所示。表1 给出了2 种VSG 控制策略的RGA 分析结果对比，表中Δλ11为传统VSG 控制策略与改进VSG 控制策略的相对增益差，为标幺值。

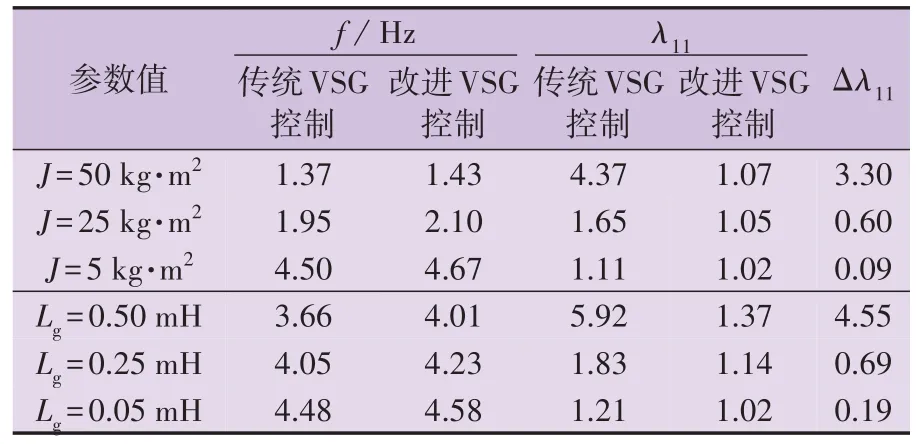
表1 2种VSG控制策略的RGA分析结果对比Table 1 Comparison of RGA analysis results between two VSG control strategies

由图A8、A9 可知，在不同的虚拟惯量J和电网电感Lg下，相较于传统VSG控制策略，采用改进VSG控制策略后，VSG 控制环路间的相对增益λ11大幅减小，而振荡频率变化较小，这表明采用改进VSG 控制策略可有效抑制VSG 控制环路间的交互作用。由表1 可知，虚拟惯量J和电网电感Lg越大，则相对增益差Δλ11越大，这表明VSG 控制环路间的耦合作用越强，改进VSG 控制策略的振荡抑制效果越明显。

4 仿真验证

为验证采用RGA 定量分析VSG 控制环路间交互作用的正确性及所提改进VSG 控制策略的有效性，基于MATLAB／Simulink 搭建图A3 所示的仿真模型，系统参数设置如表B1所示。

4.1 RGA结果验证

依次改变虚拟惯量J，对VSG1的有功功率指令Pref1施加幅值为20 kW，频率分别为1、2、4、8 Hz的正弦扰动。在上述仿真工况下VSG2有功功率响应曲线如图6 所示，VSG2有功功率响应曲线幅值如表2所示。不同D和Lg下VSG2有功功率响应曲线幅值分别如附录B表B2、B3所示。

表2 不同J下VSG2有功功率响应曲线幅值Table 2 Active power response curve amplitudes under different values of J

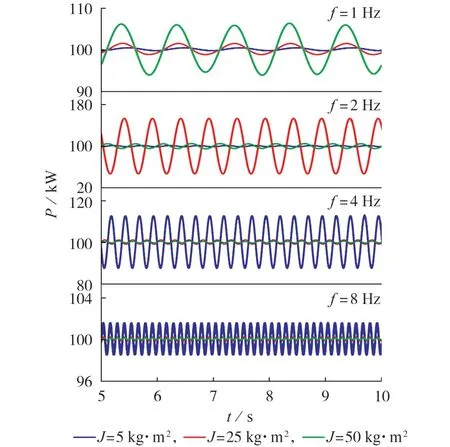
图6 不同J下VSG2有功功率响应曲线Fig.6 Active power response curves of VSG2 under different values of J

由图6以及表2和表B2、B3可知：在不同的虚拟惯量下，当施加相同幅值、不同频率的正弦扰动时，VSG 有功功率响应幅值差别较大，这是由于不同频率点的VSG 控制通道间的功率交互作用不同；振荡频率附近的功率响应幅值相对较大，低频和高频之间的耦合相对较弱；不同虚拟惯量、阻尼系数和电网电感下的VSG 响应幅值变化与1.2 节RGA 定量分析的结果一致，这表明了所提RGA 定量分析方法的正确性。

4.2 改进VSG控制策略的振荡抑制效果验证

由第3 章的RGA 分析结果可知，在各参数谐振点处，不同电网阻抗下的振荡抑制效果比不同虚拟惯量下的振荡抑制效果更明显。为验证所提改进VSG控制策略对控制环路间功率交互作用的抑制效果，对不同虚拟惯量和不同电网电感下施加幅值为20 kW、频率分别为2 Hz和4 Hz的正弦扰动，其余仿真工况设置与4.1 节相同。不同虚拟惯量下采用改进VSG 控制策略前后施加2 Hz 正弦扰动时VSG2有功功率响应波形的对比结果如附录A 图A10 所示，幅值对比结果如附录A图A11（a）所示。不同Lg下采用改进VSG 控制策略前后施加4 Hz 正弦扰动时VSG2有功功率响应波形的对比结果如附录A 图A12所示，幅值对比结果如附录A图A11（b）所示。

由图A10 和图A11（a）可知，相较于采用改进VSG控制策略前，采用改进VSG控制策略后，当施加2 Hz 的正弦扰动时，不同虚拟惯量下VSG2有功功率响应幅值均有所降低，其中，J=25 kg·m2时的有功功率响应幅值降低为105 kW，此时，控制环路间的耦合作用可以忽略。由图A12 和A11（b）可知，当施加4 Hz 的正弦扰动时，采用改进VSG 控制策略可以有效降低不同电网电感下VSG2有功功率响应的幅值。上述仿真分析结果与第3 章的RGA 分析结果一致，这表明在传统VSG 控制策略中引入高通滤波环节可有效增大VSG 在低频段的阻尼，进而抑制VSG 有功功率-频率控制环路间的交互作用。

5 实验验证

为了进一步验证所提改进VSG 控制策略抑制VSG 控制环路间交互作用的有效性，搭建2 台VSG并联并网系统的实验平台，如附录A 图A13 所示。相关实验参数如附录B表B4所示。

实验工况设置如下：VSG1和VSG2的初始有功功率指令Pref1=Pref2=1.5 kW，对VSG1的有功功率指令Pref1施加幅值为0.1 kW，频率分别为0.8、1.0、1.5、2.0、3.0、4.0 Hz的正弦扰动。图7给出了不同正弦扰动频率下传统VSG 控制策略和改进VSG 控制策略的有功功率响应曲线。图8 给出了传统VSG 控制策略和改进VSG控制策略的有功功率响应曲线幅值。

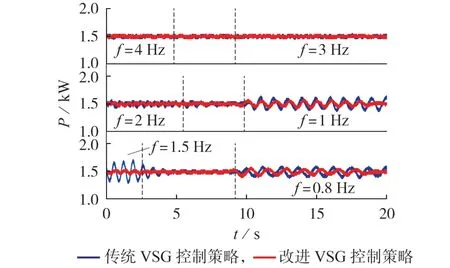
图7 不同正弦扰动频率下传统VSG控制策略和改进VSG控制策略的有功功率响应曲线Fig.7 Active power response curves of traditional VSG control and improved VSG control strategies under different sine disturbance frequencies

图8 传统VSG控制策略和改进VSG控制策略的有功功率响应曲线幅值Fig.8 Active power response curve amplitudes of traditional VSG control and improved VSG control strategies

由图7 和图8 可知，采用改进VSG 控制策略可以较好地抑制VSG 控制环路间的功率交互振荡，其中，当施加1.5 Hz的正弦扰动时，采用传统VSG 控制策略的有功功率响应幅值为170 W，而采用改进VSG 控制策略的有功功率响应幅值为40 W。此外，实验结果与RGA 分析结果一致，这表明了所提改进VSG控制策略的有效性及准确性。