基于改进Shapley值法的风-光-水-储多主体互补发电系统合作增益分配策略

2024-03-26段佳南赵心怡常逸凡葛远裕

电力自动化设备 2024年3期

段佳南，谢俊，赵心怡，常逸凡，葛远裕

（河海大学能源与电气学院，江苏南京 211100）

0 引言

开发利用可再生能源是实现“双碳”目标的重要途径。但风、光出力具有随机性和间歇性特征，其大规模接入电网时存在并网难和消纳难的问题［1］。多能互补运行是目前解决可再生能源并网与消纳问题的可行方法之一［2-3］，其核心在于如何利用水电、储能等可调节资源提升新能源系统的运行灵活性。径流式小水电站以无调节和日调节为主，调节性能较差，故目前引入储能来增强系统的灵活性已成为行业共识［4］。抽水蓄能（抽蓄）电站作为技术成熟、成本低廉的大容量储能设施，大多与风、光捆绑作为独立调节资源或与其他调节资源配合参与系统优化运行［5］。为了最大限度地消纳风电，文献［6］建立了考虑火-储深度调峰容量二次分配的分层优化调度模型；文献［7］利用水电补偿电源端的出力波动，利用抽蓄补偿系统的上网功率波动，构建了考虑光电、负荷不确定性的水-光-蓄联合优化调度模型。上述研究以小时为时间尺度，大多关注解决风、光小时级的间歇性波动问题，鲜有关注风、光秒级时间尺度快速锯齿状波动的研究。文献［8］指出阵风引起的风机短期功率剧烈波动可能会引发系统电压越限、网损增加等危害，这种剧烈波动会对系统的安全运行产生不容忽视的不利影响。变速抽蓄机组因其转速可调、调节范围更广、响应速度更快，现已被应用于平抑风、光快速功率波动的研究中［9］。但上述研究均针对变速抽蓄机组的控制策略展开，亟需研究考虑变速抽蓄控制效果的风-光-水-变速抽蓄互补发电系统的调度模型与方法。

多能互补运行为系统带来了合作增量收益（增益），制定公平的合作增益分配策略能促使多主体能源稳定形成互补运行系统［10］。合作博弈理论现已被广泛地应用于能源管理［11］、增益分配［12］等领域。Shapley 值法是传统的合作博弈分配方法，一些研究在Shapley 值法的基础上，结合优化调度的影响因素，引入综合修正系数，提出了基于改进Shapley 值法的增益分配模型［13］，此类改进能更准确地衡量个体的贡献价值，但无法克服Shapley 值法应用于大规模系统时固有的组合爆炸问题［14］。合作博弈简约算法被提出用于解决大规模利益主体的合作增益分配问题。文献［15］提出了利用奥曼夏普利（Aumann-Shapley，A-S）值法对巴西水电系统共100 座水电站的合作电量增益进行分配；文献［16］将最大最小成本法（minimum cost remaining saving，MCRS）应用于雅砻江流域风-光-水9 利益主体系统的增益电量分配问题。相较于Shapley 值法，MCRS 的求解速度更快，计算所占内存更少。上述合作博弈简约算法能较好地克服大规模利益主体增益分配时的组合爆炸问题，具备计算高效性，但当利用目前提出的高效性算法进行增益分配时，仍以成员个体为计算单位，随着系统规模持续扩大，只能将计算复杂度由指数级增长降低至线性增长，且难以进一步降低。

针对上述问题，本文以风-光-小型常规水电-变速抽蓄多主体互补发电系统为研究对象，主要围绕系统的联合优化调度、合作增益分配两大问题进行研究。考虑常规小水电机组和变速抽蓄机组的常规调节特性及变速抽蓄机组的快速调节特性，提出了兼顾系统小时级、秒级安全性的风-光-水-储多主体互补发电系统联合优化调度模型；通过资源聚合，以同类型主体为计算单位进行增益分配，对高维度问题进行降维处理，构建合作增益贡献指标作为同类型主体间细化分配的量化标准，并结合Shapley 值法以及非对称纳什谈判理论，提出了一种基于改进Shapley 值法的合作增益分配策略。最后通过算例仿真验证所提方法的高效性、可行性。

1 风-光-水-储多主体互补发电系统的联合优化调度模型

在非合作运行模式下，风电场、光伏电站、小型常规水电（小水电）、抽蓄电站（储能）分别以自身为利益主体，风、光、水按照自然资源的多寡发电上网，获取个体运行收益，抽蓄电站作为系统的调节资源，不考虑其独立承担发电任务，故无单独运行收益。在合作运行模式下，将风-光-水-储多主体互补发电系统视为一个利益主体，由抽蓄机组向系统提供旋转备用容量。为了保证互补发电系统出力安全上网，抽蓄机组配合常规小水电对电量进行储存，并共同平抑风、光小时级出力波动。利用变速抽蓄机组的快速响应特性来补偿风、光的秒级快速功率波动，实现风、光秒级出力波动的平抑。

假设某风-光-水-储多主体互补发电系统含n个利益主体，其集合记为大联盟N，S(S⊆N)为其任一子联盟，调度周期总时段数为T，下文对所有联盟组合情况下的系统统一建立优化调度模型。

1.1 风电场／光伏电站的出力预测模型

风／光出力具有随机性，地理位置相邻的风电场／光伏电站的出力具有相关性，为了综合考虑多个风／光出力的不确定性特征与相关性特征，按如下步骤构建风电场／光伏电站的出力预测模型。

1）根据中心极限定理，由于预测时间尺度为24 h，假设风／光出力服从正态分布［11］。

2）基于风／光出力历史数据样本X=[x1，x2，…，xK] （K为样本数量），利用极大似然估计法获取各风／光利益主体出力PWD/PVi的正态分布概率密度函数f(PWD/PVi)的最优似然估计参数，如式（1）所示（具体推导过程见附录A）。

式中：xi（i=1，2，…，K）为第i个风／光出力历史数据样本；μMLE、σMLE分别为正态分布的均值、标准差的最优似然估计参数。

3）根据概率密度函数进一步求解边缘分布函数F()，同一时段t内风／光出力联合概率分布可通过其边缘分布函数与高斯Copula 函数C（·）构建［14］，如式（2）所示。

式中：P为时段t风／光利益主体i的出力随机变量；ρ为风／光出力的相关系数矩阵。

4）基于高斯Copula函数与蒙特卡罗模拟法生成1 000 个风／光出力场景，取置信度为ζ，设定风／光预测出力的上限、下限分别如式（3）和式（4）所示。

式中：ω为出力场景；Ω̂WD/PV为风／光预测出力场景集合；G(ω)为场景ω出现的概率。

1.2 系统运行约束

风电场、光伏电站、小水电、抽蓄机组的运行约束较常规，具体见附录B 式（B1）—（B16）。记风电场、光伏电站、小水电、抽蓄机组集合分别为ΩWD、ΩPV、ΩHY、ΩPS。

1.2.1 系统旋转备用约束

小水电因库容受限通常难以提供备用支撑，因此由抽蓄机组向互补发电系统提供旋转备用容量，须满足的约束如下：

1.2.2 系统小时级安全性约束

为了保证系统安全运行，要求系统出力打捆上网时具备平稳性特征，虽然风、光、水出力在日内时间尺度具有自然互补特性，但只能在一定程度上平抑风、光出力波动。因此，本文考虑抽蓄机组配合小水电以实现系统小时级安全运行，调度小水电出力缓解系统上网出力波动，当其调节能力受限时，抽蓄机组通过储能来实现剩余电能在时间上的转移。以上网出力曲线的变化率、峰值、谷值作为系统小时级安全上网的评价指标［17］，具体约束如下：

式中：βWD，t、βPV，t、βHY，t、βPS，t、βt分别为时段t风、光、水、抽蓄、系统的上网出力变化率；Δt为单位时段间隔；分别为时段t风电场w、光伏电站p的上网出力；P为时段t小水电h的上网出力；P为时段t系统的上网出力；Pave为调度周期内系统的平均上网出力；Cr、Cp、Cv分别为上网出力曲线的变化率、峰值、谷值。

1.2.3 系统秒级安全性约束

风、光电出力除了在小时级时间尺度上具有间歇性波动，在秒级时间尺度上也会出现0.1PN（PN为额定功率）及以上的功率波动。在阴雨等极端天气下，风、光出力的秒级波动概率将更大［4］。小水电需通过几十秒到分钟级完成一次、二次调频，难以平抑大规模风、光的秒级功率波动。变速抽蓄机组除具备常规调峰、调频能力外，还具备百毫秒级的暂态功率支撑能力［4］，因此本文考虑利用变速抽蓄机组的快速响应能力来平抑风、光出力的秒级功率波动。为了合理利用机组的快速调节性能以及便于量化秒级功率波动，规定当风、光功率波动超过0.005PN时，须实行快速功率控制。系统秒级安全性约束具体如下：

1.3 目标函数

以系统运行收益最大为优化目标，统一建立所有联盟组合情况下的系统调度模型，见式（19）。

2 基于改进Shapley值法的增益分配模型

Shapley 值法基于利益主体自身的边际贡献价值对合作增益进行分配，分配结果满足个体理性、合作理性以及整体理性。但在实际工程中，多主体互补发电系统所包含的利益主体规模较大，采用传统Shapley值法求解时会出现组合爆炸现象。

为了解决大规模利益主体的合作增益分配问题，本文提出了一种基于改进Shapley 值法的分配策略。在合作联盟的联合优化调度中，考虑到在相同的时段内同一类型的利益主体往往具备相似的行为特性，例如：光电利益主体在正午时段出力占比最大，若其上网电价较低，为了平抑上网出力波动，最大化系统运行收益，则联盟中所有光电利益主体均将大量储能而少量上网。因此，首先将合作联盟中相同类型的利益主体进行资源聚合，打捆视作一个利益主体以削减联盟规模，并对聚合利益主体组成的所有子联盟进行优化调度求解；然后，根据调度求解结果，采用Shapley 值法进行初始分配，得到同一类型下聚合利益主体的合作增益初始分配结果；接着，在聚合利益主体内，量化各子主体在大联盟中的贡献价值，构建合作增益贡献指标；最后，以聚合利益主体的初始分配结果为基础，结合各子主体的合作增益贡献因子，采用非对称纳什谈判理论［18］进一步细化分配，获得各子主体的合作增益分配结果。

2.1 基于资源聚合的增益函数

将同类型的利益主体打捆视作一个整体，记作聚合体A（A=ΩWDorA=ΩPVorA=ΩHYorA=ΩPS），对于风-光-水-储多主体互补发电系统N，不论其规模大小，所有利益主体最终均可以聚合为4 类利益主体。根据合作博弈理论，这4 类聚合利益主体共存在24-1=15 种子联盟组合情况，记由聚合利益主体产生的子联盟为S͂，构建基于资源聚合的增益函数如下：

式中：V(S͂)为子联盟S͂合作产生的增量收益；F(S͂)为子联盟S͂合作产生的总收益；F({A})为子联盟S͂中各聚合体A单独运行时产生的收益。

2.2 基于Shapley值法的增益分配模型

基于Shapley 值法进行增益分配是以某利益主体对联盟的边际贡献价值作为增益分配的衡量标准。根据增益函数式（20）量化各聚合利益主体的边际增益贡献，构建基于Shapley 值法的增益分配模型如下：

式中：x为聚合体A初始分配所得合作增益；V(S͂ A)为子联盟S͂除去聚合体A后合作产生的增量收益；|S͂|、|N|分别为子联盟S͂、大联盟N内的主体数量；WS͂为计及各聚合利益主体加入联盟顺序的分配权重系数。

2.3 基于非对称纳什谈判的分配模型

对于同一类型的利益主体而言，通过构建若干合作增益贡献指标来综合量化个体的贡献大小。聚合利益主体内子利益主体之间以各自贡献因子作为谈判标准，从而确定细化分配结果，最终实现各利益主体公平共享联盟合作增益。具体分配步骤如下。

1）基于大联盟N的调度结果，建立合作增益贡献指标作为聚合体A内各主体之间的细化分配量化标准。

a）风／光聚合体内的合作增益贡献指标。

b）小水电聚合体内合作增益贡献指标。

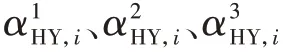
式中分别为聚合体内小水电利益主体i的发电贡献量、小时级波动平抑贡献量、上下游级联发电贡献量；P为时段t小水电利益主体i的出力；U为小水电利益主体i上一级开始所有上游小水电集合；D为小水电利益主体i下一级开始所有下游小水电集合。

c）抽蓄机组聚合体内合作增益贡献指标。

2）根据合作增益贡献指标，分别针对各聚合利益主体建立增益贡献初始矩阵，如式（25）所示。

式中：a为合作增益贡献指标的数量；k′为某类聚合体A内的主体数量。

3）根据单位电价／收益系数对各贡献指标进行影响程度修正，如式（26）所示。

式中：ψ̂k′×aA为聚合体A修正后的合作增益贡献矩阵；θj为第j个合作增益贡献指标的修正因子；λj为第j个合作增益贡献指标量化结果所对应的单位电价／收益系数。

4）归一化矩阵元素，并计算第i(i=1，2，…，k′)个主体的综合贡献价值HA，i，如式（27）所示。

式中：rij为增益贡献矩阵中的第i行第j列元素；εij为归一化后增益贡献矩阵中的第i行第j列元素。

5）计算各聚合体中每个主体的合作增益贡献因子ϖA，i，如式（28）所示。

6）结合各类聚合体的Shapley 值初始分配结果，构建基于合作增益贡献因子的风-光-水-储多主体互补发电系统非对称纳什谈判模型，如式（29）所示。

各利益主体最终分配的合作增益xNai为：

式中：F({i})为利益主体i单独运行产生的收益。

本文所提基于改进Shapley 值法的合作增益分配策略思路框架图以及具体求解步骤见附录C。

3 算例分析

本文以四川某流域规划的风-光-水-储10 主体互补发电系统为算例，选取木坡电站（额定装机容量为45 MW）、杨家湾电站（额定装机容量为60 MW）、猛固桥电站（额定装机容量为54 MW）这3 座日调节水电站，分别记作HY1、HY2、HY3，其在地理位置上形成级联关系，集合记作ΩHY；选取已建成以及规划中的风电场和光伏电站各3 座，其中风电场WD1、WD2、WD3的装机容量分别为20、20、30 MW，集合记作ΩWD，光伏电站PV1、PV2、PV3的装机容量分别为50、50、30 MW，集合记作ΩPV；选取1 台全功率变速抽蓄机组，记作PS。根据2022年夏季的风／光历史出力数据、秒级功率波动数据（聚合为小时级波动系数）以及某日水电站的天然来水数据，建立风-光-水-储10 主体互补发电系统的联合优化调度模型（时段间隔为1 h，1 d被分为24个时段）。基于高斯Copula函数对风／光出力进行随机模拟，置信度取为95 %，风／光出力预测上下限模拟结果见附录D 图D1。其他相关参数取值见附录D 表D1 — D4。本文的优化调度以及合作增益分配均采用MATLAB R2016a软件调用Gurobi进行求解。

3.1 不同运行模式下的调度结果分析

对风-光-水-储10 主体互补发电系统进行联合优化调度，其中小时级安全上网的评价指标设定为Cr=0.15、Cp=Cv=0.18。对比非合作、合作运行模式下各利益主体的收益和成本，结果见表1。

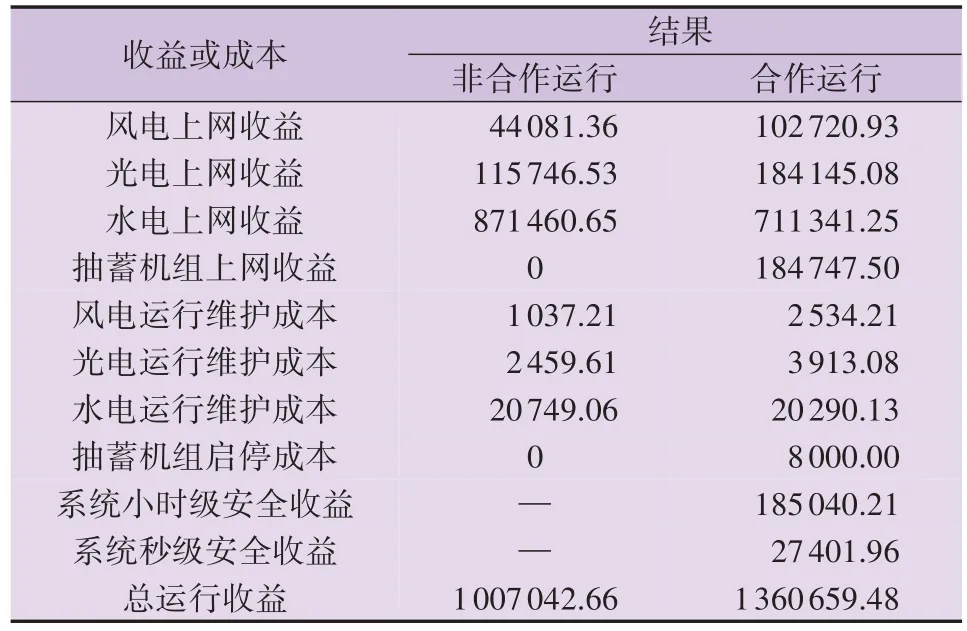
表1 非合作、合作运行模式下各利益主体的收益和成本Table 1 Benefits and costs of each stakeholder under non-cooperative and cooperative operation modes单位：元

由表1 可知，在合作运行模式下，抽蓄机组为系统提供上下旋转备用容量，支撑消纳风／光预测波动出力，风电、光电利益主体均在非合作运行模式的基础上增发电量，因此相较于非合作运行模式，合作运行模式下的风电、光电上网收益均有所提升，运行维护成本也相应有所增加。对于水电利益主体而言，为了平抑系统小时级出力波动，其除了调整自身出力计划外，还在系统发电高峰时段将电能大量储存于抽蓄机组，因此相较于非合作运行模式下水电出力全部上网，合作运行模式下的水电直接上网收益有所减少；且由于库容受限，在联合优化调度时水电少量弃水，总出力减少，因此合作运行模式下的水电运行维护成本稍有降低。在合作运行模式下，抽蓄机组存储系统多余的电能，实现电量在发电峰谷时段之间的转移，从而产生了上网收益与启停成本，相较于非合作运行模式，合作运行模式下系统的总运行收益提高，产生了35.1 % 的增量收益。

在联合优化运行调度中，抽蓄机组分时储能以配合水电灵活调节，平抑系统小时级上网出力波动。在安全上网评价指标的约束下，非合作、合作运行模式下的系统总上网电量曲线以及合作运行模式下各机组的发电量结果如图1 所示。由图可知：在合作运行模式下，抽蓄机组在系统发电高峰时段（时段8 — 17）从风、光、水电获取功率以抽水储能，水电站HY1、HY3在该时段内调节并减少自身出力；在时段1 — 7、18 — 24，抽蓄机组发电上网，水电站适当增加出力以平抑系统中风、光出力的间歇性。对比图中的系统总上网电量可知，合作运行模式下的系统总上网电量曲线更加平稳，峰谷差值由非合作运行模式的47.84 MW·h减少为19.53 MW·h。

图1 运行调度结果Fig.1 Operating and scheduling results

图1 中的红色曲线表明，非合作运行模式下系统上网电量的秒级波动特征明显。在合作运行模式下，变速抽蓄机组利用快速调节特性，在日内可平抑的风、光快速功率波动分别为风电场装机容量的42.6 %、光伏电站装机容量的45.1 %，秒级时间尺度内的上网电量曲线更加平滑，实现了系统的秒级安全性保障。以当前风、光出力秒级波动为参照设置基础场景，将波动率扩大3 倍、5 倍、7 倍、9 倍，可求得合作运行模式下的系统运行收益分别为182.64、197.86、200.63、200.63 万元。由此可知，风、光出力秒级波动越剧烈，合作运行模式下的系统运行收益越高，但当秒级波动持续增强，抽蓄机组的快速控制能力受限，无法进一步平抑风、光波动，因此合作运行模式下的系统运行收益不再增长且系统上网电量的秒级波动开始增强。

3.2 基于改进Shapley值法的合作增益分配结果

首先将系统中同类型的利益主体进行聚合，形成风-光-水-储4 利益主体系统，对其组成的15 种联盟组合情况进行优化调度求解。根据增益函数式（20），各子联盟的增量收益求解结果见附录E表E1。

根据各子联盟的增量收益求解结果，以大联盟的合作增益为分配基础，采用Shapely 值法进行初始分配，求得风电、光电、水电、抽蓄聚合利益主体的合作增益分别为58 315.51、65 985.75、108 152.66、121 162.92 元。原系统中仅有1 个抽蓄机组利益主体，因此抽蓄机组的增益分配结果可直接求得。下面根据合作增益贡献指标，采用非对称纳什谈判理论分别对风电、光电、水电聚合利益主体中的各主体进行进一步细化分配。求得：风电聚合利益主体中，各主体的合作增益贡献因子分别为0.32、0.27、0.41；光电聚合利益主体中，各主体的合作增益贡献因子分别为0.40、0.39、0.22；水电聚合利益主体中，各主体的合作增益贡献因子分别为0.44、0.31、0.25。经计算，各利益主体的合作增益分配结果满足个体理性以及整体理性，具体见附录E图E1。

3.3 增益分配方法的对比分析

为了验证本文所提增益分配方法的可行性，将其与MCRS 以及A-S 值法这2 种高效分配方法进行对比，从求解精度、计算效率两方面进行分析。

3.3.1 增益分配方法的求解精度分析

MCRS、A-S 值法均以个体对联盟的边际贡献价值作为分配的衡量标准。A-S 值法将各利益主体的发电资源等分为若干分段，每一分段都被视为独立的利益主体参与Shapley 值分配，当分段数量越大时，A-S 值法的分配结果越精确。MCRS 省略了部分子联盟的求解，将个体边际贡献简单量化为最大收益与最小收益之差，因而求解存在一定的偏差。因此，以多分段下A-S 值法的求解结果作为参照，绘制互补发电系统在不同分段数量下A-S 值法的合作增益分配结果，如图2所示。

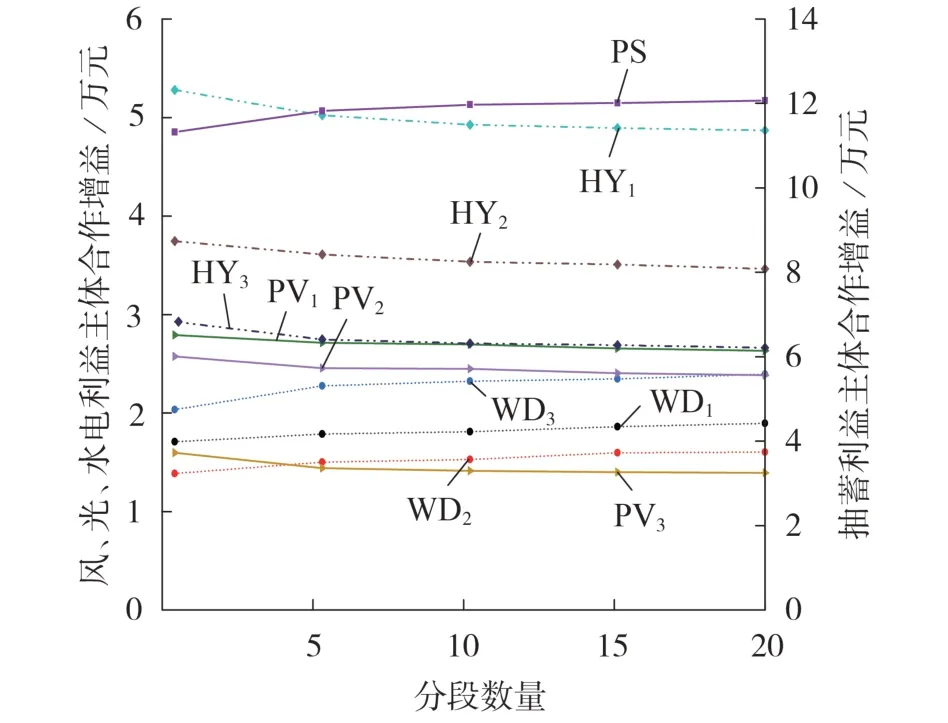
图2 不同分段数量下A-S值法的合作增益分配结果Fig.2 Cooperative synergistic benefit allocation results ofA-S value method under different numbers of segment

由图2 可见，采用A-S 值法时，各利益主体的合作增益分配结果随着分段数量的增大而逐渐精确。当分段数量为5 时，分配结果快速收敛；当分段数量达到20 时，认为各利益主体的合作增益分配结果趋于稳定。

以分段数量为20 时A-S 值法的分配结果为基准，将本文所提改进Shapley值法、MCRS的分配结果与之对比，计算相对误差率，结果如表2 所示。由表可知，当采用改进Shapley 值法进行增益分配时，除个别主体（WD1）外，其余利益主体的合作增益分配结果更接近A-S 值法（20 分段）的分配结果，计算误差率均小于MCRS 的误差率。从整体而言，改进Shapley 值法的总误差率较MCRS 降低了65.57 %，求解精度更高。

表2 3种方法的分配结果对比Table 2 Comparison of allocation results among three methods

3.3.2 增益分配方法的计算效率分析

增量分配方法的计算耗时包含联盟调度计算耗时、增益分配计算耗时两部分。其中，增益分配部分均为基本运算，求解速度较快，因此各分配方法的计算耗时主要取决于所需优化调度的联盟数量。以联盟求解数量以及计算总耗时作为计算效率的衡量标准，3 种方法的计算效率对比如表3 所示，表中M为A-S值法的分段数。

表3 3种方法的计算效率对比Table 3 Comparison of calculation efficiency among three methods

由表3 可知，A-S 值法的计算耗时＞MCRS 的计算耗时＞改进Shapley 值法的计算耗时。基于A-S 值法的合作增益分配方法除需求解n个利益主体的独立运行结果外，仅需对大联盟进行1 次优化调度求解，但由于求解精度与分段数M呈正相关，为了达到一定的精度，还需对大联盟进行不同分段数量情况下的循环调度求解，因此A-S 值法的计算精度越高，计算耗时越长。本文所提改进Shapley 值法不论系统中个体数量多少，通过资源聚合，将风-光-水-储大规模系统聚合为风-光-水-储4 利益主体系统，仅需求解15 种联盟组合的调度情况，计算效率大幅提高。MCRS需对n个利益主体的独立运行模式、除去个体成员的n种合作运行模式以及大联盟合作运行模式进行求解，计算效率居中。

对于包含风、光、水、储4 种能源类别的算例系统而言：A-S值法和MCRS的计算复杂度随着系统规模的扩大呈线性增长，这是因为所需求解的联盟数量随着利益主体的数量呈线性扩大，计算耗时增长明显；改进Shapley 值法所需求解联盟数量不随利益主体数量的增大而进一步扩大，计算量会少许增长，但该增长是由利益主体数量增多而导致调度模型求解时长增加引起的。

当系统包含的能源种类增多时，本文所提方法聚类所得能源聚合体增多，计算复杂度上升。此时对于小规模系统而言，本文方法的计算高效性优势不明显；当系统规模较大、利益主体数量较多时，由于本文方法的核心思想为“聚类”，计算高效性优势将凸显。

综上，当系统能源种类一定时，系统规模越大，即联盟成员数量越多，本文所提改进Shapley 值法的计算高效性优势越明显。