基于新能源-负荷相似性的源荷储协调调峰优化调度

2024-03-26李凤婷周远翔

电力自动化设备 2024年3期

王婷，李凤婷，周远翔，3，崔巍

（1.新疆大学电气工程学院，新疆乌鲁木齐 830047；2.新疆农业大学机电工程学院，新疆乌鲁木齐 830052；3.清华大学电机系，北京 100084；4.国网宁夏电力有限公司超高压公司，宁夏银川 750000）

0 引言

对于以新能源作为电能主要提供者的新型电力系统［1］而言，其源侧资源呈现强随机性和波动性，负荷侧设备的用电行为具有较强的时变性及随机性［2］，源荷双侧的不确定性对电网的调峰能力提出了更高的要求。

大量研究表明，源荷储协调调度能提升电网的调峰能力［3-5］。文献［6-7］提出了含风、光、水、火、储系统的源储调峰调度策略，文献［8-11］建立了计及价格型、激励型需求响应的源荷储深度调峰调度模型。然而，价格型需求响应在各时段的负荷响应量受参与用户的随机性、调节目标的模糊性影响而存在不确定性［12］；激励型需求响应只能缓解负荷高峰时期电网的调峰压力，很难满足新型电力系统对需求侧发挥调节能力的迫切要求。接入负荷调控系统的负荷聚合商、虚拟电厂等可调节负荷能够按照电网的调度指令参与调节［13］，可有效解决价格型需求响应和激励型需求响应存在的不确定性、局限性问题。

已有较多关于可调节负荷参与电网优化调度的研究：文献［14］以可调节负荷用电调节总量与风电总出力增量之间的差值最小化为目标，对日前荷源计划功率曲线进行优化，以提高风电利用率；文献［15］以系统下调峰需求与可调节负荷调节量的差值最小为目标优化可调节负荷。上述研究均以可调节负荷调节量与电网调节需求量的差值最小作为可调节负荷响应目标，在电网调节需求较小时优化效果较好，然而新型电力系统的调峰需求量不断增大且变化频繁，采用上述方法难以达到各时段调节效果最优的目标。

负荷曲线与新能源出力曲线相似，可减少传统机组的启停、爬坡次数，维持机组出力趋于平稳［16］。目前，已有学者针对新能源-负荷（new energy resource-load，NER-L）曲线的相似性问题进行了研究。文献［17］基于欧氏距离和动态时间归整距离建立了NER-L 相似性度量指标，并利用其刻画高比例新能源电力系统的负荷特性。文献［16］基于改进的欧氏距离、动态时间归整距离建立了NER-L 相似度指标和波动度指标，并将指标作为源荷储协调优化模型的约束条件。虽然学者们对NER-L 相似性进行了一些研究，但建立的度量指标在刻画NER-L 时序相似性、形状相似性方面表现不佳，对于实现源荷储协调调峰的指导性不强。

考虑到NER-L 相似性对电网优化调度的促进作用，本文将NER-L 相似性引入可调节负荷与风光火储的协调调峰优化调度中，提出了一种基于NERL 相似性的源荷储协调调峰优化调度方法。首先，探究了NER-L相似性对电网调峰的影响，基于NERL 相似性建立可调节负荷响应目标，以实现缩小净负荷峰谷差、缓解电网调峰压力的目的；然后，建立了基于相关系数的NER-L 相似性指标，构建了源荷储协调调峰双阶段优化调度模型，第一阶段以NERL 相关系数最大作为优化目标，第二阶段以弃风弃光量最小和系统运行成本最低作为优化目标；最后，以IEEE 30 节点系统为算例进行仿真分析，验证本文所提模型的有效性。

1 NER-L相似性对电网调峰的影响

新型电力系统源荷双侧的不确定性会导致负荷峰谷时段不断变化。负荷峰谷差相等的不同运行场景下新能源发电及负荷曲线见附录A 图A1，对应的净负荷峰谷差见附录A 表A1。可见：运行场景1 下的新能源、负荷曲线波动较为平缓，但两曲线增减变化模式的相似性以及曲线形状的相似性均较低，导致净负荷峰谷差较原始负荷峰谷差增大，增大了电网的调峰难度；虽然运行场景2 下的新能源、负荷曲线波动较剧烈，但负荷曲线对新能源曲线的跟踪匹配程度较好，两曲线增减变化模式的相似性以及曲线形状的相似性较高，因此净负荷曲线较为平缓，净负荷峰谷差较原始负荷峰谷差显著减小，降低了电网调峰难度。由上述分析可知，新能源曲线与负荷曲线相似，可平滑净负荷曲线，降低净负荷峰谷差。

因此，本文提出了利用可调节负荷的调节特性优化电网负荷曲线，基于NER-L 相似性建立可调节负荷响应目标，以平滑净负荷曲线，缩小净负荷峰谷差，降低新型电力系统的调峰难度。

2 NER-L相似性指标的建立

在对NER-L 相似性进行度量时，聚焦于NER-L时序相似性（即两序列点的增减变化模式相同）与NER-L 形状相似性（即两序列中具有相同的形状）。常用的相似性度量方法包括闵可夫斯基距离、欧氏距离、曼哈顿距离、切比雪夫距离、动态时间归整距离、杰卡德指数、相关系数等，其中：闵可夫斯基距离、欧氏距离、曼哈顿距离、切比雪夫距离等距离函数虽易于理解、计算简单，但其不能辨别形状相似性，不能有效体现动态变化趋势的相似性；动态时间归整距离由于不满足三角不等式关系，不能成为度量函数［18］；杰卡德指数是两序列间共有元素的占比，不能满足NER-L 相似性的度量要求；通过计算两序列协方差与标准差的商，可得到两序列的相关系数，其绝对值越接近于1，表示两序列的相关性越大，在用于度量数值维度上移动或缩放的两曲线相似性时精度较高。因此，本文采用基于相关系数的度量方法度量NER-L 曲线相似性，用相关系数作为NER-L相似性指标。

将一个调度周期分为T个时段，一个调度周期内的新能源发电功率序列PN={Pn1，Pn2，…，PnT}，其中Pni（i=1，2，…，T）为时段i的新能源发电功率，Pni=分别为时段i风电场j、光伏电站k的发电功率，NW、NP分别为风电场、光伏电站的数量。一个调度周期内的负荷用电功率序列PL={PL1，PL2，…，PLT}，PLi为时段i的负荷用电功率。基于相关系数可得到NER-L 相似性指标R(PN，PL)的计算公式，如式（1）所示。

式中：cov(PN，PL)为新能源发电功率与负荷用电功率的协方差；Vvar[PN]、Vvar[PL]分别为新能源发电功率、负荷用电功率的方差分别为风电场j、光伏电站k在一个调度周期内的平均发电功率；为在一个调度周期内的负荷平均用电功率。

R(PN，PL)的取值范围为［-1，1］，其数值可以准确地刻画负荷对新能源出力的跟踪匹配程度：当负荷曲线与新能源曲线的变化趋势相同时，R(PN，PL)为正值；当负荷曲线与新能源曲线的变化趋势相反时，R(PN，PL)为负值；当负荷曲线与新能源曲线的变化趋势接近完全的单调相关时，|R(PN，PL) |会增大，当完全单调相关时，|R(PN，PL)|=1；当负荷曲线与新能源曲线的变化趋势没有相关性时，R(PN，PL)=0。

3 基于NER-L 相似性的源荷储协调调峰双阶段优化模型

3.1 基于NER-L 相似性的源荷储协调调峰双阶段优化调度思路

接入调控系统的可调节负荷资源具有可控性强、调度成本低、低碳环保等优点，利用可调节负荷优化电网负荷曲线可有效缩小净负荷峰谷差，提升新能源利用率，降低电网调峰难度，因此可调节负荷作为优先调峰资源参与电网优化调度。虽然新型电力系统中的火电机组容量占比逐渐减小，但火电机组具有调控技术先进、运行稳定、运行成本较低的优点，将其作为常规调峰资源参与电网优化调度。储能装置通过适时充放电可进一步缩小净负荷峰谷差，提升新能源利用率，降低火电机组的调峰压力，但储能的装机容量小，运行成本较高，且频繁调用会影响其使用寿命，因此储能装置在常规机组调峰压力较大或新能源弃电率较高时段才参与调峰。

综合考虑可调节负荷的调节特性、新能源的运行特性、火电机组的深度调峰能力和储能装置的运行特性，本文提出了基于NER-L 相似性的源荷储协调调峰双阶段优化调度模型，其思路如图1所示。

图1 双阶段优化调度模型思路Fig.1 Idea of two-stage optimal scheduling model

第一阶段优化模型结合风电／光伏预测功率、负荷预测数据、可调节负荷功率数据及其约束条件，以NER-L 相关系数最大为目标，平滑净负荷曲线，缩小净负荷峰谷差。通过优化求解得到最优电网负荷及各时段可调节负荷的响应功率，并将其传递至第二阶段优化模型。

依据优化后的电网负荷，第二阶段优化模型综合考虑火电机组运行成本、风电及光伏运行成本、弃风弃光惩罚成本、可调节负荷运行成本、储能运行成本，计及火电机组约束、风电及光伏约束、储能约束，以弃风弃光量最小、调峰运行成本最低为目标对各机组及储能出力进行优化，通过优化求解得到各机组及储能的最优出力。

3.2 基于NER-L 相似性的可调节负荷响应功率及电网负荷优化

3.2.1 目标函数

第一阶段优化模型以NER-L 相关系数F1最大为目标函数，如式（5）所示。

式中：PN，P、PLF、PAR，F分别为一个调度周期内新能源预测发电功率序列、刚性负荷功率序列、可调节负荷响应功率序列；Pni，P、PLFi、PAR，i，F（i=1，2，…，T）分别为时段i新能源预测发电功率、刚性负荷功率、可调节负荷响应功率分别为时段i风电场j、光伏电站k的预测发电功率；R(PN，P，PLF+PAR，F)的计算参考式（1）—（4）。

3.2.2 约束条件

负荷聚合商、虚拟电厂等可调节负荷按照聚合整体参与调峰优化调度，因此第一阶段优化模型需满足可调节负荷功率约束，如式（10）所示。

式中：PAR，i，min、PAR，i，max分别为时段i可调节负荷的最小、最大功率。

第一阶段优化模型以风电／光伏预测功率、负荷预测功率、可调节负荷预测功率数据为基础，考虑可调节负荷功率约束，以NER-L 相关系数最大为目标，并在MATLAB 中进行单目标优化求解，可获得优化后的可调节负荷响应功率序列PAR，F及优化后的电网负荷序列PLF+PAR，F。通过第一阶段模型的优化可高效精准地调用可调节负荷，实现平滑净负荷曲线、降低电网调峰难度的目的。

3.3 源储协调调峰优化

3.3.1 目标函数

第二阶段优化模型以弃风弃光量最小和调峰运行成本最低为目标。

1）目标1：弃风弃光量最小。

为了提升新能源的利用率，以弃风弃光量最小为优化目标，如式（11）所示。

式中：F2为弃风弃光量；分别为时段i风电场j、光伏电站k的实际发电功率。

2）目标2：调峰运行成本最低。

以调峰运行成本最低为优化目标，如式（12）所示。

式中：F3为调峰运行成本；fTh、fW、fP、fS、fAR分别为火电机组、风电、光伏、储能、可调节负荷的运行成本；fcw为弃风弃光惩罚成本。

a）火电机组运行成本fTh：在不同的调峰阶段，火电机组参与调峰的成本均不相同。

常规调峰成本f1、深度调峰机组损耗成本f2、深度调峰机组稳燃投油成本f3可分别表示为：

式中：Nt为火电机组数量；an、bn、cn为火电机组n的耗量系数；Pn，Th，i为时段i火电机组n的出力；Scoal为当季的单位煤炭价格；β为火电机组的运行影响系数；Sunit，n为火电机组n的购置成本；Nf(P)为由转子低周疲劳曲线确定的转子致裂循环周次；Qoil，n，i为时段i火电机组n深度调峰的投油量；Poil为当季油价。

综上，火电机组运行成本fTh可表示为：

式中：Pn，Th，max为火电机组n的最大出力；Pn，Th，a为火电机组n常规调峰技术的最小出力；Pn，Th，b为火电机组n不投油调峰稳燃时的最小出力；Pn，Th，c为火电机组n投油调峰时的最小出力。

b）风电运行成本fW可表示为：

式中：PWIND为单位功率风电发电成本。

c）光伏运行成本fP可表示为：

式中：PPV为单位功率光伏发电成本。

d）弃风弃光惩罚成本fcw可表示为：

式中：ω1、ω2分别为弃风、弃光惩罚系数。

e）储能运行成本fS可表示为：

f）可调节负荷运行成本fAR可表示为：

式中：Pprice为单位功率可调节负荷运行成本。

3.3.2 约束条件

第二阶段优化模型的约束条件包括功率平衡约束、各电源及储能运行约束，具体见附录A 式（A1）—（A11）。

第二阶段优化模型综合考虑了调峰运行成本及运行约束条件，以弃风弃光量最小、调峰运行成本最低为目标，可采用改进的非支配排序遗传算法在MATLAB 中对模型进行求解，以确定火电机组、风电、光伏、储能的最优出力。

4 算例分析

4.1 基本数据与参数

采用IEEE 30 节点系统作为算例分析对象，系统包括4台火电机组（总容量为2 900 MW）、1座容量为800 MW 的风电场、1 座容量为500 MW 的光伏电站，新能源装机容量占总装机容量的29.2 %，储能容量为250 MW。

模型参数设置如下：常规火电机组的参数见附录A 表A2；新能源预测曲线及负荷预测曲线见附录A 图A2；可调节负荷在各时段的可调功率为总负荷的10 %，可调节负荷成本为350 元／（MW·h）；储能电站的初始储能量为220 MW·h。以上述数据为基础，基于本文所建模型，在MATLAB 中对源荷储协调调峰进行计算分析。

4.2 优化调度结果分析

通过对第一阶段和第二阶段模型的优化求解，可得到优化后的NER-L相似性指标R(PN，PL)=0.99，电网调峰运行成本为1 992.0 万元，新能源弃电功率为375.1 MW。优化前、后的NER-L 相关关系以及NER-L 曲线分别如附录A 图A3 和图A4 所示，电网净负荷曲线、火电机组出力曲线、新能源弃电功率及弃电率分别如图2 — 4所示。

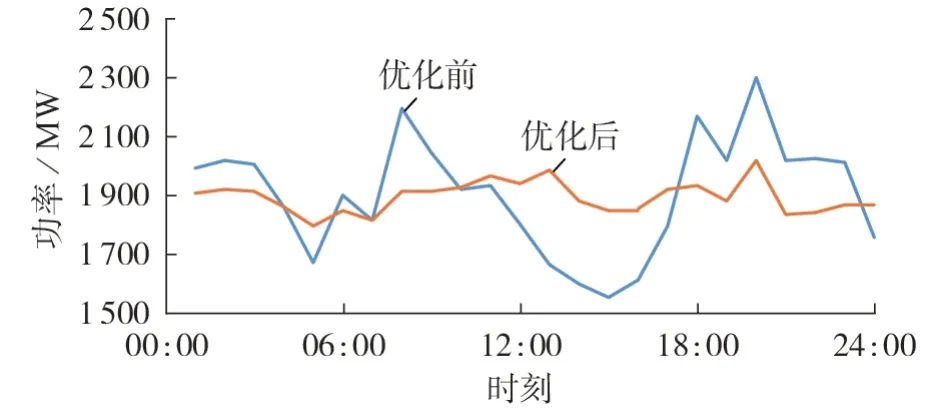
图2 优化前、后电网净负荷曲线Fig.2 Net load curves of power grid before and after optimization

由图A3和图A4可知，优化前、后的NER-L相似性指标R(PN，PL)分别为0.87、0.99，相较于优化前，优化后的NER-L 相似性指标有显著上升，且几乎达到了最大值。优化后的NER-L 曲线在形状、时序方面高度相似，实现了负荷对新能源出力的精准跟踪、时序匹配目标。由图2 可看出，优化前、后的电网净负荷峰谷差分别为747.3、219.0 MW，且优化后净负荷曲线在调度周期内的波动次数及幅度均降低，可见以NER-L 相关系数最大作为可调节负荷的响应目标，缩小了净负荷峰谷差，平滑了电网净负荷曲线。由图3 可看出，各火电机组的最小出力均大于常规调峰出力下限，火电机组在调度周期内均为常规调峰，未进入深度调峰运行状态。由图4 可看出：在新能源出力最大时段（13:00 — 15:00），弃电功率较大，最大弃电功率达到102.7 MW，弃电率为0.6 %；在其他时段，弃电功率均小于40 MW，弃电率均小于0.2 %；在整个调度周期内，总弃电功率为375.1 MW，弃电率为2.1 %，可见新能源的整体消纳水平较高。

图3 火电机组出力曲线Fig.3 Output curves of thermal power units

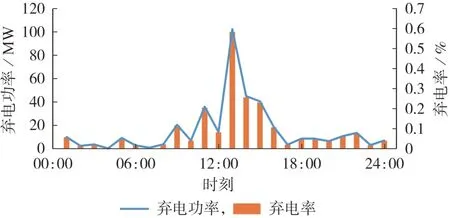
图4 新能源弃电功率及弃电率Fig.4 Abandoned power and abandoned power rate of new energy

4.3 不同调度模型的对比分析

为了验证本文所提模型的经济性及有效性，以表A2、图A2 的数据为基础，选择以下3 种模型进行对比分析：①模型1，以弃风弃光量最小和调峰运行成本最低为目标，不考虑负荷，进行源储协调调峰；②模型2，以弃风弃光量最小和调峰成本最低为目标，考虑价格型需求响应，进行源荷储协调调峰，其中峰谷平时段划分参考文献［9］，各时段的需求响应功率为总负荷的10 %，各时段的需求响应成本均为350元／（MW·h）；③模型3，考虑NER-L相似性的含可调节负荷的源荷储协调调峰，即本文模型。

为了分析NER-L 相似性对电网调峰的影响，对比不同模型的净负荷曲线及净负荷峰谷差，分别如图5 和表1 所示。由图5 和表1 可以看出：模型1 和模型2 的净负荷曲线波动次数较多，波动幅度较大；模型3 的净负荷曲线波动幅度较小，曲线较为平缓。模型3 的净负荷峰谷差仅为219.0 MW，远远小于模型1 和模型2 的净负荷峰谷差。由此可见，模型3 有效地缩小了净负荷峰谷差，平滑了净负荷曲线。

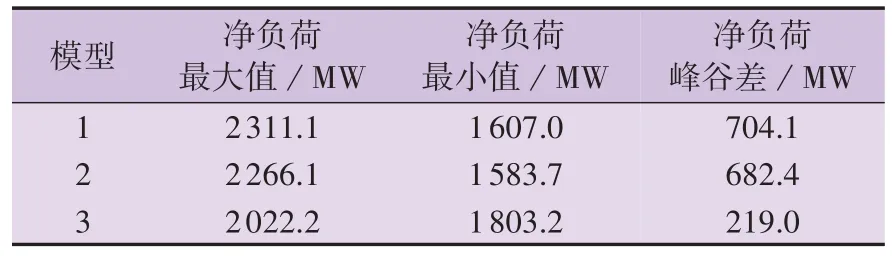
表1 不同模型的净负荷峰谷差对比Table 1 Comparison of net load peak-valley difference among different models

图5 不同模型的净负荷曲线对比Fig.5 Comparison of net load curve among different models

为了进一步分析本文模型对电网调峰经济性及新能源利用率的促进作用，对不同模型的运行成本及弃电功率进行对比，结果分别如表2 和表3 所示。由表2和表3可以看出，相较于模型1，模型2、模型3的调峰运行成本增大，火电机组运行成本减小，弃电率及弃电功率显著降低。分析可知，模型2和模型3增加的调峰运行成本主要为负荷调节成本，负荷调节降低了新能源弃电率，由此可见通过调节负荷侧用电特性可以减少火电机组的运行成本，同时提高新能源利用率。

表2 不同模型的运行成本Table 2 Operation cost of different models

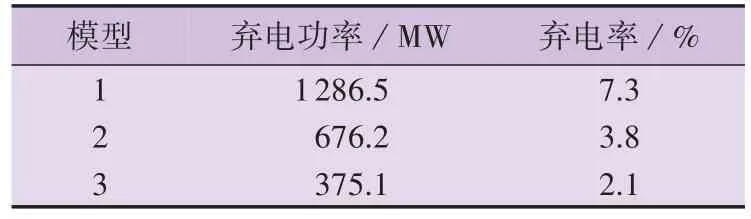
表3 不同模型的弃电功率及弃电率Table 3 Abandoned power and abandoned power rate of different models

分析模型2 和模型3 的调峰运行成本及弃电数据可以看出，相较于模型2，模型3 的调峰运行成本减少了16.6万元，风电运行成本增大了19.4万元，其他运行成本均小于或约等于模型2 的结果。模型3的风电运行成本较高是因为：相较于模型2，模型3的弃电功率、弃电率均较低。由上述分析可知，模型3 以较低调峰运行成本获得了较高的新能源利用率，在提升新能源利用率及经济性方面优势明显。