新能源大基地风光储容量协调优化配置

李明轩，范 越，汪 莹，王 炜，牛拴保，魏 韡

（1.清华大学 电机工程与应用电子技术系，北京 100084；2.国家电网有限公司西北分部，陕西 西安 710048）

0 引言

随着能源技术的革新与全球能源形式的变化，我国如今正面临能源发展改革的新局面。全力发展光伏、风电等可再生能源是我国完成电力系统改革、实现“双碳”目标的必要途径［1］。新能源基地通常需配置储能以应对新能源出力的随机性［2-3］，而合理的风光储容量配比有助于发挥各类电源的互补特性，保证系统经济、可靠运行。因此，在规划阶段如何合理配置各类电源及储能的容量是一个重要的研究问题。

对于新能源与储能的规划，现有研究从风光配比［4］、火电机组退役［5］、新能源出力波动［6］、多主体共建共享模式［7］、多目标优化［8］、新能源不确定性［9-10］等多个角度出发，提出了各具针对性的规划方法。然而，现有关于容量配置的研究主要面向新能源网内消纳的场景，不适用于新能源大规模外送的情形。大型新能源外送基地的规划是近年来出现的一类新问题。在“双碳”目标驱使下，我国于近年开始着力规划大型新能源外送基地的建设，将西北等地区的海量风光资源产生的电能外送至东部地区。其中一个代表性工程为2022 年底启动的“沙戈荒”风光火储基地项目，其为我国首个千万千瓦级大型新能源基地项目，拟将西北地区生产的清洁能源经直流通道外送至京津冀地区，预计每年外送4.4×1010kW·h电能。可以预见，在能源转型背景下，我国将陆续推进类似的大型新能源外送基地的开发。而考虑新能源外送策略的风光储容量配置将随之成为一个具有显著应用价值的研究内容。

相比于新能源网内消纳问题，新能源外送是一种全新的场景。与新能源网内消纳不同，新能源的直流外送一般采用点对点的输电模式，不涉及电网潮流方程，但是需要充分考虑直流输电的运行特性，对直流外送的运行模式进行有效建模；此外，新能源网内消纳问题聚焦于发电、负荷的实时平衡，而新能源外送的重点在于如何有效满足预定的外送计划，其外送电量及联络线运行计划通常需要提前确定，具有显著的计划性。综上所述，新能源外送问题在考虑的因素、建模方式等方面均有一定的独特性，现有的容量配置方法不能直接应用。

在新能源跨区直流外送方面：文献［11-13］分别从安全约束经济调度、受端电网调峰裕度、碳排放量等不同角度出发，提出了风光火一体化外送调度模型；文献［14］基于不同的电力交易模式，分析了跨区直流外送模式对新能源消纳的影响；文献［15］考虑风电消纳量以及弃风限电风险，提出了风火打捆外送的多目标优化调度方法；文献［16］基于短路容量对直流送端电网的运行方式进行了优化。然而，上述研究均集中于日前调度策略的优化，不涉及新能源基地的容量配置。大型新能源外送基地的规划建设是近2 年新出现的一类工程问题，目前相关研究较少。文献［17］研究了大型新能源外送基地的电源规划问题，但其仅考虑了年度的送电量约束，未考虑具体场景的送电可靠性。为了保证实际外送功率能够充分满足预定的直流外送计划，应建立有效的送电可靠性指标，并在此基础上进行容量配置研究。

不同于现有研究，本文对大型新能源外送基地这一新场景下的风光储容量配置问题进行了探索，提出了一种送电置信概率指标，基于此构建了面向新能源可靠外送的风光储容量配置模型。该模型得到的规划方案能够有效地满足直流外送计划。考虑到新能源出力分布的不确定性，提出了分布鲁棒规划模型，并针对其中分布鲁棒约束中存在的整数变量问题，提出了一种迭代求解算法。所提模型与方法可为新能源基地的容量配置问题提供重要参考。

1 问题描述

风光储联合规划是保证高比例可再生能源电力系统安全高效运行的重要问题。合理的风光配比可充分发挥风电、光伏的互补特性，减少新能源整体出力的波动性；储能的配置则有助于进一步平抑新能源出力波动，实现能源的稳定外送，提高新能源消纳能力。而风光出力的不同波动特性会导致在不同的风光配比下对储能的需求不同，由此就产生了风光储容量优化配置问题。

本文所研究的新能源外送基地模型如图1 所示，该系统主要由风电、光伏、火电、储能构成。新能源基地发出的电能由高压直流输电线路进行外送。出于工程实际考虑，本文研究问题中的直流通道容量、火电容量均为确定量，而风电、光伏、储能容量为待规划变量，主要原因是：高压直流通道的建设周期较长，需在较长的时间尺度下提前规划，且通道容量主要受输电距离、电压等级等因素影响，因此直流通道容量在本文问题中为已知量；在发电侧方面，火电资源在减排目标下往往是提前规划的，因此火电容量亦为已知量。火电、光伏、风电发出的电能均可通过高压直流通道向外送出，也可将多余的电能存入储能设备中。此外，为了保证高比例新能源系统下的送电可靠性，避免极端出力场景导致规划结果过于保守的问题，可能存在其他送端电网的支援通道，以协助该系统完成输电计划。为了避免长期向其他电网索取额外电量，支援功率需满足周期性电量平衡约束，即在指定的周期（如1 周）内支援的净电量等于0。如果系统中不存在支援，则在建模时直接将各时段的支援量设置为0。

图1 新能源外送基地模型Fig.1 Model of renewable energy transmission base

对于我国西部等可再生能源富足的地区，发电侧提供的大量电能需通过直流通道向其他负荷密集区域送电。本文主要研究大型新能源外送基地的风光储容量配置问题，所配置的风光储资源应保证新能源可靠外送，其中需考虑如何模拟典型场景的新能源外送计划、如何基于典型场景外送计划对新能源外送的可靠性进行建模这2个关键因素。

1.1 直流输电计划功率

在新能源外送的高压直流输电工程中，受端电网通常不会配置大规模新能源机组，受端系统的负荷主要由火电进行供应。而在“双碳”背景下，我国的火电将逐步退出运行，此时负荷主要由直流通道输送的清洁能源进行供应，而受端电网中有限的火电资源仅需用于填充剩余的负荷缺口，不再是发电计划的主要组成部分。综上所述，直流输电计划功率应与负荷曲线尽可能接近，以满足受端电网的调峰需求。因此对于典型场景的新能源外送计划制定，其核心问题在于如何在满足直流输电运行模式的条件下使得外送计划尽可能地满足受端电网的负荷需求。

根据上述分析，本文基于受端电网的负荷曲线构建优化问题，制定典型直流输电计划，具体思路如下：首先，对受端电网负荷曲线进行聚类，得到典型的负荷场景；然后，针对每一种负荷场景制定相应的典型直流输电计划，使得直流通道的计划功率与负荷曲线尽可能相近。

负荷曲线的聚类可采用K-means 聚类算法［18］得到。其中，类别数K可由肘点法确定，该方法主要基于类别数对误差平方和的影响判断合适的K值，当类别数K增大对误差平方和的影响较小时，对应的点即为肘点。

基于K-means 聚类算法可得到K类典型负荷场景，从而可为每一类典型负荷场景设计相应的直流输电计划。在高压直流输电中，考虑到联络线运行稳定性、设备运行寿命等因素，输电功率不应频繁波动［19］。本文的直流输电计划采用经典的“直线式”运行模式，这是目前我国特高压直流外送采用的主要模式［12］。在该模式下，大部分时段的直流通道输送功率保持不变，以保证直流通道安全、稳定运行，仅在少数时段切换通道输电功率，且通常每天最多切换2 次通道输电功率。因此，每一类典型负荷场景对应的直流输电计划功率需满足如下约束：

式中：T为1 d 的时段数，本文中取值为24；ut为0-1变量，ut=1 表示时段t调整直流通道输电功率，ut=0表示时段t不调整直流通道输电功率；为时段t的直流输电计划功率；M为大M 法的系数；I为当前场景类别对应的负荷曲线数量；为第i条负荷 曲线在时段t的取值；Δt为单位时段时间间隔，本文中为1 h。式（1）表示每天最多进行2 次输电功率调整；式（2）为日间运行连续性约束，要求日初、日末的直流输电计划功率相等，从而使跨日输电功率保持连续，减少功率切换；式（3）为输电功率切换约束，当ut=0 时，应保证时段t直流输电计划功率保持不变；式（4）为电量平衡约束，即直流通道的计划电量供给应与受端电网负荷保持平衡，以避免能量供给缺额或过剩。

此外，直流输电计划功率应与负荷曲线尽可能相近，以最大化直流通道的利用效率。基于上述考虑，对于每一类负荷场景，分别构建式（5）所示混合整数二次规划问题以得到相应的直流输电计划功率。

该方法可有效保证直流输电计划功率与受端电网的负荷曲线相匹配，使得主要的负荷功率可由直流输电满足，而直流输电功率与负荷之间的些许差额则可由受端电网的电源、储能进行配平。

1.2 送电置信概率

在实际运行中，新能源基地的实际外送功率应尽可能满足制定的直流输电计划，而如何有效地衡量新能源外送可靠性则是一个重要问题。为此，本文提出了送电置信概率指标，以衡量新能源的外送可靠性。本文将送电置信概率定义为：1 d内所有时段的新能源基地实际外送功率均满足直流输电计划的概率。在实际应用中，可基于历史数据选取足量典型日的风电、光伏、负荷曲线生成场景集，从而基于场景集评估送电置信概率。当给定送电置信概率α时，相应的送电置信概率约束为：

式中：ρ=[ρ1，ρ2，…，ρN]T为N维概率分布向量，ρn（n=1，2，…，N）为场景n出现的概率，N为场景总数；z=[z1，z2，…，zN]T为N维0-1 向量，zn=0 表示场景n为完全送电场景，即1 d内所有时段的实际外送功率均满足直流输电计划，zn=1 表示场景n为不完全送电场景，即存在未达到直流输电计划功率的时段。式（6）表示不完全送电场景出现的概率不超过1-α，即完全送电场景出现的概率大于α。如果取α=1，则要求运行优化问题中的全部场景均为完全送电场景。

上述送电置信概率约束有效地衡量了新能源的外送可靠性，可为新能源系统的规划提供参考。

2 模型构建

基于式（5）、（6）—（8）可建立风光储容量规划模型。本章首先构建风光储容量配置的基本规划模型，然后考虑场景分布的不确定性，构建分布鲁棒规划模型。

2.1 风光储容量配置的基本规划模型

假设各场景下新能源基地的输电计划已基于1.1节制定。以此为背景，应对新能源基地的风光储容量进行合理配置，使得实际运行中的新能源外送可靠性得以满足，即各场景下的系统出力能够以较高的置信度满足外送计划。由此，可基于1.2节所提送电置信概率约束构建风光储容量配置模型。

基于图1 所示风光储联合规划系统，构建基本规划模型，需满足的约束条件如下。

1）新能源出力约束。

新能源出力约束包括各时段的光伏、风电出力上下限约束，具体表达式分别见附录A 式（A1）和式（A2）。

2）火电出力约束。

火电出力约束包括火电出力上下限约束、爬坡约束，具体表达式分别见附录A式（A3）和式（A4）。

3）储能运行约束。

储能运行约束包括储能电量状态方程、储能电量上下限约束、储能功率上下限约束、储能充放电互补松弛约束。其中储能电量状态方程为：

式 中：en，t为 场 景n中 时 段t储 能 存 储 的 能 量；、分别为场景n中时段t由光伏、风电、火电向储能输送的功率；为场景n中时段t储能向直流通道输送的功率；η为储能的充放电效率。值得说明的是，相邻场景之间的储能电量应保证连续性，即en，T与en+1，1也应满足储能电量状态方程式（9）。储能电量上下限约束、储能功率上下限约束、储能充放电互补松弛约束见附录A式（A5）—（A10）。

4）新能源弃电率约束。

新能源弃电率约束表示新能源基地的弃风、弃光率不能超过指定的阈值，具体表达式分别见附录A式（A11）和式（A12）。

5）新能源出力占比约束。

新能源出力占比约束表示新能源出力占风电、光伏、火电整体出力的比例不能低于指定的阈值，具体表达式见附录A式（A13）。

6）电网支援功率约束。

7）送电置信概率约束。

基于上述各类约束，可得到考虑送电置信概率的风光储联合规划模型为：

式中：Finv为总投资成本；Ps、Pw分别为光伏、风电的装机容量；Pe、Ee分别为储能的额定充放电功率、额定容量；cs、cw分别为光伏、风电单位功率投资成本；cp、ce分别为储能单位功率、单位容量投资成本。上述风光储容量配置的基本规划模型为混合整数线性规划问题，可采用现有的优化求解器进行求解。

2.2 分布鲁棒规划模型

2.1节的基本规划模型只考虑了参考概率分布，认为各场景出现的概率均相同。而在实际应用中，为了使规划结果更加安全、有效，有必要进一步考虑场景分布的不确定性，保证极端场景分布下新能源的可靠供应。

基于上述考虑，本文进一步建立了风光储容量配置的分布鲁棒规划模型。考虑场景分布的不确定性，建立模糊集，将约束式（13）更换为式（16）所示约束。

式中：D∞为场景分布模糊集；参数θ影响模糊集D∞的规模，需人为设定。文献［20］针对参数θ的取值提供了一个有效的参考方案，即如果希望真实的概率分布ρ以置信水平β落入模糊集D∞中，则参数θ可根据式（18）取值。

值得一提的是，由于约束式（16）需对模糊集中D∞的任意概率分布ρ均成立，式（16）实际上对应于无限多个约束，这使得优化问题难以直接求解，需将其转化为可以求解的形式。文献［21］基于对偶原理将形如式（16）和式（17）的分布鲁棒约束转化为可求解的形式。然而，该方法仅适用于分布鲁棒约束中变量为连续变量的情况。对于本文问题中的约束式（16），z为整数变量，此时强对偶定理不再成立，因此无法采用文献［21］中的常规方法对式（16）进行转化。

为了解决上述问题，本文提出了一种迭代算法对式（16）进行转化，在每一次迭代中加入当前规划结果对应的极端场景约束，从而使原优化问题式（15）可求解。首先定义初始场景概率分布集Ω={ρ(0)}，然后在第k次迭代中将新的场景概率分布ρ(k+1)加入集合Ω中，该场景基于本次迭代中求解规划问题得到的整数解z(k)生成，其对应于当前规划结果下的最恶劣场景。具体而言，若z(k)的第n个分量=1，则说明场景n没有完全满足计划送电功率，为了保证下一次迭代中规划结果的鲁棒性，应基于式（17）尽可能地提高场景n对应的概率，即令=+θ，得到新的场景概率分布ρ(k+1)。然后检验当前的最优解z(k)是否满足(ρ(k+1))Tz(k)≤1-α，若满足，则说明该次迭代的规划结果能够保证其对应的最恶劣场景下的可行性，从而模糊集中其他场景的可行性也自然得以满足，因此规划的鲁棒性得以保证，算法结束；否则，说明鲁棒性没有得到满足，将ρ(k+1)加入场景集合中，进行下一次迭代。

所提迭代算法的流程图如附录B 图B1 所示。该算法在每次迭代中产生的场景概率分布ρ(k)均为模糊集D∞中的极点，对应于D∞中的极端场景。如果规划结果能够满足所有极端场景，则其亦能够满足D∞中的其他场景。因此，该规划结果满足鲁棒性。

3 算例分析

以西北电网为算例进行仿真分析。算例部分参数见附录C 表C1。参数取值主要以我国河西第2个特高压直流工程的实际情况为参考。西北电网2021 年的归一化风电、光伏出力曲线统计特征的箱线图分别见附录C图C1和图C2，图中的风电（光伏）的归一化出力是指实际出力与风电（光伏）容量之比。受端电网负荷曲线的统计特征如附录C 图C3所示。基于上述历史数据生成场景集，进行风光储容量配置。为了有效考虑风光出力季节性的影响，对风光火储运行约束采用8 760 h 连续运行的方式进行建模，即各日之间具有时序性；而场景集则用于分布鲁棒置信概率约束式（16）的构建，以分析最坏场景分布下的送电可靠性。

3.1 直流输电容量优化

基于负荷曲线制定直流输电计划。首先采用Kmeans聚类算法对负荷曲线进行聚类，当类别数K分别设定为2 — 5 时，误差平方和见附录C 图C4。从图中可以看出，K=4对应的点可认为是肘点，此时再增大类别数K，误差平方和的变化不明显，因此将负荷聚类的类别数确定为4。由此得到负荷聚类结果，如图2所示。

图2 负荷聚类结果Fig.2 Load clustering results

对图2 中的4 类负荷曲线分别构建直流输电容量优化问题式（5），得到各类负荷曲线所匹配的直流输电计划功率，如图3 所示。可基于所得输电计划进行满足送电可靠性要求的风光储容量配置。

图3 4类负荷曲线所匹配的直流输电计划功率Fig.3 Direct current transmission planning power for four types of load curves

3.2 风光储容量基本规划结果

得到直流输电计划后，将各场景的负荷需求替换为相应的直流输电计划功率，基于2.1节的基本规划模型进行风光储容量规划。将送电置信概率α分别设为0.95 和1.00，将电网支援系数设为0（即不存在电网支援），求解优化问题式（15），得到规划结果如表1所示。

表1 不同α取值的规划结果Table 1 Planning result with different values of α

由表1 可知，将送电置信概率由0.95 提升至1.00 会显著增加风光储规划容量及投资成本，而这是由极少数的极端场景所导致的，会使结果过于保守，难以具备参考价值。因此，基于全部场景进行规划的结果过于保守而缺乏实际意义，而本文所提的送电置信概率概念对于风光储规划具有一定的应用价值，通过设置合适的置信概率指标可有效保证规划结果的合理性。

此外基于实际工程的考虑，固定风光配比，设定送电置信概率为0.95 进行风光储容量规划，结果如表2 所示。由表可知：相比于最优配置方案，过度增大光伏的占比会显著增加相应的储能配置容量及总投资成本；而当风光配比接近2∶1 时，有助于发挥风电、光伏的互补出力特性，优化资源配置。

表2 固定风光配比时的容量规划结果Table 2 Capacity planning results with fixed wind-photovoltaic ratio

进一步地引入电网支援，重新进行计算，设置送电置信概率为0.95，不固定风光配比，在不同支援系统下进行规划，所得规划结果如附录C 表C2 所示。由表可知，支援系数的增大可以显著减小储能容量配置与总投资成本，说明新能源外送基地可在一定程度上增加与其他系统的互联与协调，避免极端场景导致规划结果过于保守的问题，提高规划运行的经济性、高效性。

除了投资成本以外，一些规划模型还会在目标函数中考虑火电运行成本。考虑、不考虑火电运行成本时的规划结果如附录C 表C3 所示。由表可知，考虑火电运行成本会使风电、光伏容量有所增大，投资成本有所提升，这是因为考虑火电运行成本会在一定程度上减少火电发电量，增加新能源出力需求，因而提高了新能源的容量配置需求。此外，是否考虑火电运行成本对风光配比结果的影响不大，这是因为风光配比主要由新能源自身出力特性所决定。

为了进一步展现算例分析的一般性，对算例参数进行灵敏度分析，在表3所示3组投资成本参数下分别进行容量规划。以参数1为基准，参数2降低了风电、光伏单位功率投资成本，而参数3 则增加了储能单位功率／容量投资成本。3 组参数的规划结果如表4所示。参数2的规划结果表明，当新能源建设成本较低时，会在一定程度上增加新能源容量配置，减少储能容量配置，但是对风光配比的影响不大。参数3 的规划结果表明，储能单位功率／容量投资成本的提升对规划结果的影响较小，这是因为新能源基地对储能的依赖性较高，需要使储能与新能源配合完成送电计划，因此在储能单位功率／容量投资成本提高的情况下配置的储能容量基本保持不变。

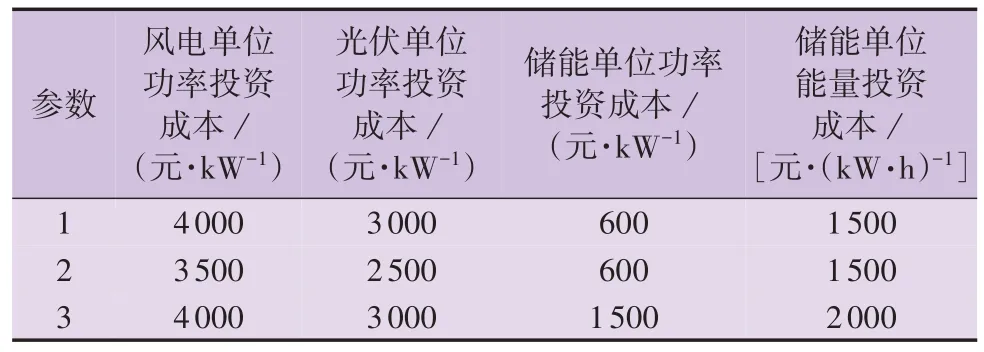
表3 3组投资成本参数Table 3 Three groups of investment cost parameters

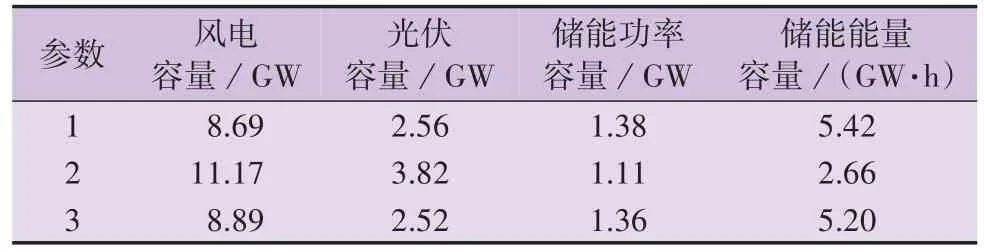
表4 不同参数下的规划结果Table 4 Planning results under different parameters

3.3 风光储容量分布鲁棒规划结果

3.2节的分析是基于参考概率分布进行的，即认为各场景出现的概率均相同。本节进一步考虑场景分布的不确定性，采用2.2 节所提分布鲁棒规划模型，使得规划结果能够满足不确定集合式（17）中任意场景分布下的送电可靠性。

本节同样基于西北电网算例进行分析，其中设置送电置信概率为0.95，电网支援系数为5 %，不固定风光容量配比。分布鲁棒规划模型中，场景总数N=365，参考概率分布ρ(0)n=0.002 74，式（18）中的置信水平β=0.05，模糊集规模参数θ=0.004 0，从而各场景概率ρn的取值范围为[0，0.006 74]。基于2.2节所提迭代算法进行分布鲁棒规划，在每次迭代中加入当前规划结果对应的极端场景分布，经过50 次迭代达到收敛。第1、2、50 次迭代得到的规划结果如表5 所示。迭代过程中规划成本的变化情况如附录C 图C5 所示。可见，在第2 次迭代中基于极端场景对规划结果进行了较为显著的调整，而后续的迭代则进一步基于极端场景对结果进行微调，使得规划结果在式（17）所示模糊集中的任意分布下均能够满足送电可靠性要求。在求解时间方面，本文所提迭代算法的计算时长为14.6 h，平均每次迭代的计算时长为17 min。该计算时长对于长时间尺度规划问题是可以接受的。

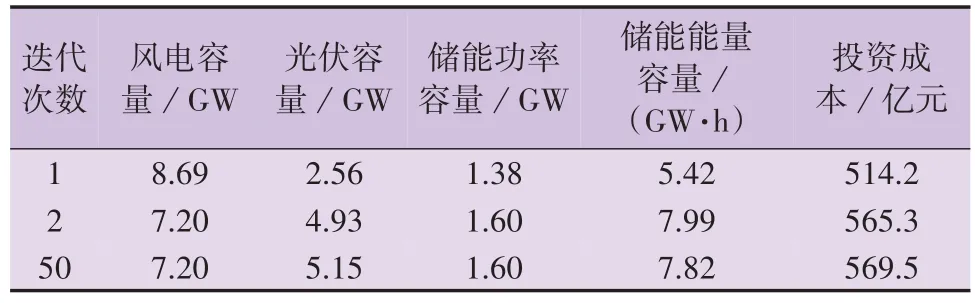
表5 分布鲁棒规划结果Table 5 Distributionally robust planning results

此外由表5 可知，在迭代过程中风电容量有所减小，光伏容量增大。这是因为风电出力波动性较大，在考虑极端场景分布时大规模风电容量配置会为送电可靠性带来挑战，而减少风电、增加光伏有助于缓解该问题。可见，本文所提分布鲁棒规划模型能够有效地计入场景分布的影响，保证不同场景分布下的送电可靠性。

为了进一步验证本文所提分布鲁棒规划模型的效果，从式（17）所示模糊集中随机采样得到200 种场景分布。对于每一次迭代的规划结果，测试这200 种场景下优化问题式（15）的可行性，即检验给定容量配置方案下是否具有满足式（15）中各运行约束的可行解。相应的计算结果如附录C 图C6 所示。结果表明：对于第1 次迭代对应的规划结果，200 种场景中有72 种场景不具备可行的全年运行方案，这是因为基本规划结果仅考虑了参考概率分布场景，而没有考虑较坏场景下的送电可靠性；相较而言，迭代后得到的规划结果能够满足全部采样场景下的送电可靠性，验证了所提分布鲁棒规划模型的有效性。

4 结论

本文研究了大型新能源外送基地的风光储容量优化配置问题，在进行风光储联合规划时考虑了直流外送策略对新能源系统规划的影响。基于负荷需求优化直流外送计划，进而提出送电置信概率指标，用于衡量新能源外送可靠性；在此基础上，建立了风光储容量配置模型，并提出了考虑场景分布不确定性的分布鲁棒规划模型及其求解算法。算例分析展现了所提容量配置方法的应用效果，所得结论如下。

1）本文研究场景具有典型性。在新能源外送场景下，所提送电置信概率指标及分布鲁棒规划模型对风光储容量规划具有一定的参考价值。在合理的送电置信概率指标下进行规划，有助于保证新能源外送可靠性，同时也能避免极端场景导致规划结果过于保守的问题，保证容量配置的合理性。

2）在最优容量配置方案中，风电容量为光伏容量的2～3 倍。而在分布鲁棒规划模型中，随着恶劣场景的不断引入，光伏容量逐渐提升，风光配比有所下降。此外，在最优容量配置方案下，储能功率容量约为新能源装机容量的15 %，充电时长为4～5 h。该配置方案符合工程实际，可为新能源大基地的容量配置提供有效参考。

本文的容量配置方法可为我国大型新能源基地的建设提供参考。后续将进一步研究考虑不确定性的容量优化配置高效求解算法。

附录见本刊网络版（http：//www.epae.cn）。