基于互Box-Cox变换和Markov链风速云模型的发电系统充裕度评估

安 睿，缪书唯

（三峡大学 电气与新能源学院，湖北 宜昌 443002）

0 引言

风能具有无污染、分布广的优点，且其发电成本低，各国出台鼓励政策，这使得全球风电装机容量迅速增长，截至2022 年，全球风电累计装机容量达到906 GW，其中，我国风电装机容量位居世界第一［1］。

随着风电在电源结构中所占比例的不断提高，准确评估风电场对电力系统充裕度的贡献尤为重要，风电容量可信度是衡量该贡献的重要指标，国内外学者已对风电容量可信度的评估方法进行深入研究。例如：文献［2］基于非时序Monte Carlo 模拟法评估含风电场的发输电系统可靠性，并根据有效载荷能力的衡量标准对同时考虑风电相关性和输电约束的风电容量可信度进行评估；文献［3］提出一种求解有效载荷能力的改进粒子群优化算法，并结合时序Monte Carlo 模拟法评估风电和储能系统的容量可信度；文献［4］将Copula 函数与弦截法相结合，建立计及相邻风电场相关性的容量可信度评估方法，并通过IEEE-RTS79 测试系统验证该方法的正确性和有效性。

准确评估风电并网系统的充裕度是计算风电容量可信度的前提，而建立合理、准确的风速模型则是评估过程中基础且关键的环节，但风速具有随机性、自相关性等特点，这给风速模型的准确建立带来了挑战。有研究使用参数分布模型计及风速随机性，例如：文献［5］应用Weibull、Gamma 等4 种概率分布模型对宁夏回族自治区某处风电场小时级风速概率分布进行拟合，结果表明，Gamma 分布在拟合小时级风速概率分布时具有较高的精度；文献［6］提出基于混合半云模型的风速建模方法，并对广东沿海某风电场的风速概率分布进行拟合，结果表明，混合半云模型在拟合风速概率分布时具有精度高、适用性强的特点。此外，有研究使用时间序列模型、随机过程、Markov 链等计及风速自相关性，例如，文献［3］应用自回归滑动平均（auto-regressive and moving average，ARMA）模型计及实测风速样本的自相关性，并结合常规机组和储能系统建立基于时序Monte Carlo 模拟法的风储联合系统可靠性模型；文献［7］在互转换Ornstein-Uhlenbeck 过程的基础上建立风速仿真模型，并通过实例验证该模型能够准确计及实测风速样本的自相关性；文献［8］在传统一阶Markov 链的基础上引入风速的季节特性、干湿特性和日特性，提出改进的一阶Markov 链风速时间序列模型，结果表明，该模型能够较精确地计及实测风速样本的自相关性。

现有研究以风速随机性和自相关性为切入点，对风速模型进行了大量研究，但仍存在如下不足：参数分布模型，如Weibull、Gamma、Rayleigh 等，需要对风速概率分布进行先验假设，但由于风速的随机性，其实际分布可能与假设分布不符，这会对风速随机性的建模造成较大误差；部分风速模型未对风速变化区间进行明确约束，可能使仿真风速样本的变化区间与实测风速样本的变化区间不匹配，例如，混合半云模型和ARMA模型可能产生与风速物理属性相悖的负值仿真风速样本；较少研究同时计及了风速随机性和自相关性。

混合半云模型已被应用于风速仿真［9］和风速概率分布拟合［10］领域，然而，混合半云模型未对风速样本的区间进行约束，可能产生与风速物理属性相悖的负值风速样本，此外，该模型得到的风速样本间的自相关性较低，可能难以描述实测风速样本的自相关性。

本文针对混合半云模型的不足，在文献［9］混合半云模型的基础上进行改进，应用互Box-Cox变换和Markov 链约束仿真风速样本的区间，使得仿真风速样本具备自相关性，提出计及风速随机性和自相关性的风速仿真模型。由于时序Monte Carlo 模拟法计算量小，且能真实反映系统的实际运行情况，将该方法与本文的风速仿真模型结合，提出计及风速随机性和自相关性的风电并网系统充裕度评估方法。最后，基于美国某观测站的实测风速样本对所提模型和方法进行验证。

1 基于互Box-Cox变换和Markov链的风速云模型

本文应用Box-Cox 变换将实测风速样本变换为服从正态分布的实测云滴样本，通过逆向云发生器求取其期望EX、熵EN和超熵HE，将其变化区间等分为K组，得出K组云滴区间的Markov链，再结合正向云发生器和转移率矩阵推导各云滴区间内仿真云滴样本的分布函数，据此产生仿真云滴样本，最后应用逆Box-Cox 变换将其变换为仿真风速样本。本文将风速样本与云滴样本间的Box-Cox变换和逆Box-Cox变换过程称为互Box-Cox 变换。基于互Box-Cox 变换和Markov 链风速云模型的建模流程如附录A 图A1所示。

1.1 风速样本与云滴样本的互Box-Cox变换

本文利用互Box-Cox 变换建立风速样本与云滴样本间的变换关系。假设收集到N组实测风速样本，记为v1—vN，利用Box-Cox 变换将N组实测风速样本变换为服从正态分布的N组实测云滴样本，由于一般形式的Box-Cox 变换要求原始数据大于0，而实测风速样本中存在零风速，因此本文使用带有位移常数的Box-Cox变换形式［11］，如式（1）所示。

式中：rt（t= 1，2，…，N）为vt经Box-Cox 变换后得到的第t组实测云滴样本；C为使vt+C＞ 0 的位移常数；λ为Box-Cox变换参数，其值可由文献［12］的极大似然估计法确定。

对Box-Cox变换求逆，即可得到逆Box-Cox变换，如式（2）所示。

1.2 K组云滴区间的Markov链

将实测云滴样本的变化区间［rmin，rmax］等分为K组，即［rmin，rmin+Δr）、［rmin+Δr，rmin+2Δr）、…、［rmin+（K-1）Δr，rmax］，并将其按顺序编号为区间1 —K。其中：rmin、rmax分别为实测云滴样本的最小值和最大值；Δr=(rmax-rmin)/K为云滴区间的长度。本文应用Markov链描述各云滴区间内云滴样本的随机转移关系，进而计及实测云滴样本的自相关性。实测云滴样本由区间（ii=1，2，…，K）向区间 （jj=1，2，…，K）的转移概率为：

式中：N（i，j）（i，j=1，2，…，K）为实测云滴样本由区间i转移至区间j的次数。

根据式（3）可得出K组云滴区间的转移率矩阵P为：

由此，若已知当前时刻云滴样本所处区间，则可根据转移率矩阵P抽样确定下一时刻云滴样本所处区间。由于风速样本与云滴样本间的互Box-Cox 变换关系，该Markov 链也可计及风速样本的自相关性。

1.3 云滴区间内仿真云滴样本的概率分布

由正向云发生器所产生的仿真云滴样本服从均值为EX、方差为E2R的正态分布N（EX，E2R）。其中，ER服从均值为EN、方差为H2E的正态分布N（EN，H2E）［14］。将经过Box-Cox 变换后得到的N组实测云滴样本代入逆向云发生器中，可计算出实测云滴样本的EX、EN和HE，具体计算公式如附录A 式（A1）、（A2）所示。因此，区间i内仿真云滴样本的概率分布为N（EX，）按区间［rmin+（i-1）Δr，rmin+iΔr］截断后得到的截断正态分布（truncated normal distribution，TND），本文将其记为TND（EX，E2R，rmin+（i-1）Δr，rmin+iΔr）。仿真云滴样本分布函数Ψ(r̂)的表达式［15］为：

式中：r̂ ∈ ［rmin+（i-1）Δr，rmin+iΔr］为区间i内的仿真云滴样本；Φ（·）为正态分布N（EN，E2R）的分布函数。通过整理式（5）可得到区间i内仿真云滴样本的逆分布函数Ψ-1(U1)为：

式中：Φ-1（·）为正态分布N（EN，E2R）的逆分布函数；U1为［0，1］区间均匀分布的随机数。由此，若已知当前时刻云滴样本所处区间，则可将随机数U1代入式（6）中，抽样得到该区间内的一组仿真云滴样本。

1.4 风速仿真步骤

首先，利用式（1）将实测风速样本转换为实测云滴样本，并根据式（A1）、（A2）求得实测云滴样本的EX、EN、HE；然后，给定实测云滴样本等分的区间数K，利用式（4）得到K组云滴区间的Markov 链转移率矩阵，并结合各云滴区间内仿真云滴样本的概率分布，抽样得到仿真云滴样本；最后，利用式（2）将仿真云滴样本转换为仿真风速样本。详细的抽样步骤如下。

1）给定仿真风速样本数量M和初始时刻仿真云滴样本所处区间w（w∈｛1，2，…，K｝）。需要注意的是，M不一定等于N，即仿真风速样本的数量M可任意给定。

2）分别产生服从正态分布N（EN，H2E）的随机数ER和［0，1］区间均匀分布的随机数U1，将两者代入式（6），生成区间w内的仿真云滴样本r̂。

3）根据仿真云滴样本所处区间w和转移率矩阵P，抽样确定下一时刻仿真云滴样本所处区间b，抽样过程如图1所示，图中U2为［0，1］区间均匀分布的随机数。利用转移率矩阵P中第w行K个元素p（w，1）—p（w，K）按顺序逐个相加的结果将［0，1］区间划分为K段，并通过判断U2所处区间确定下一时刻仿真云滴样本所处区间，例如，图1中随机数U2位于区间2，则下一时刻仿真云滴样本处于区间2，即b=2。类似地，只需确定当前时刻仿真云滴样本所处区间和转移率矩阵P，即可通过随机数U2判断下一时刻仿真云滴样本所处区间。

图1 下一时刻仿真云滴样本所处区间的抽样示意图Fig.1 Schematic diagram of sampling in interval of simulated cloud droplet sample at next moment

4）若产生的仿真云滴样本数量小于M，则令w=b，并返回步骤2）；否则将得到的M个仿真云滴样本r̂1—r̂M代入式（2）中，经过逆Box-Cox 变换得到M个仿真风速样本v̂1—v̂M。

2 基于互Box-Cox变换和Markov链风速云模型的风电并网系统充裕度及风电容量可信度评估

2.1 风速自相关性对充裕度评估结果的影响

本节假设常规机组发电容量和负荷需求恒定，分析具有不同自相关系数的风速样本对风电并网系统充裕度评估的影响。不同风速自相关系数下风电并网系统可用容量和系统负荷需求仿真曲线的3 个场景如图2 所示。图中：E为任意可用容量；从场景1 到场景3，风速自相关系数由大变小。3 个场景下的风速样本值不变，仅改变风速样本在时间轴上的前后顺序，进而改变风速自相关性的强弱，此时风速自相关性直接影响可用容量曲线的自相关性。假设A1—A3分别为场景1 — 3下可用容量曲线滞后1 h的自相关系数，可得A1—A3分别为0.84、0.41、0.04。假设ηLLO、ηLLD、ηENS分别为失电次数、失电持续时间和失电量，由图2 可知：3 个场景下阴影部分面积和所占总时段相同，这表明风速自相关性强弱不影响ηENS和ηLLD；而随着风速自相关系数的减小，场景2和场景3 下的ηLLO分别增加至3 次和4 次，这表明若忽视风速自相关性，则将导致对ηLLO的低估。

图2 不同风速自相关系数下风电并网系统可用容量和系统负荷需求仿真曲线的3个场景Fig.2 Three scenarios of simlative curves of available capacity and system load demand for wind power integrated system under different wind speed autocorrelation coefficients

2.2 充裕度评估步骤

本文将基于互Box-Cox 变换和Markov 链的风速云模型与时序Monte Carlo 模拟法结合，提出风电并网系统的充裕度评估方法。

在利用时序Monte Carlo 模拟法进行风电并网系统充裕度评估时：首先，获取所有机组的启停循环过程；其次，将本文仿真风速样本代入风电转换函数，得到风电机组的时序出力，并通过将两者组合得到系统的发电容量曲线；然后，将系统的发电容量曲线叠加至小时负荷曲线上，得到系统的可用裕度模型；最后，通过统计缺电情况计算充裕度指标。详细步骤如下。

1）假设初始时刻所有发电机组均处于正常运行状态。

2）对所有发电机组处于当前运行状态（运行或停运）的持续时间进行抽样，其中第k台发电机组处于运行或停运状态的持续时间Dk如式（7）所示。

式中：Rk为第k台发电机组在［0，1］区间均匀分布的随机数；ωk为第k台发电机组的故障率或修复率，若机组在当前时刻处于运行状态，则ωk为故障率，否则ωk为修复率。

3）根据1.4节产生仿真风速样本，并结合风电机组的启停状态和风电转换函数计算风电场的可用容量PWF，如式（8）所示。

式中：NWF为运行风电机组的数量；v̂为仿真风速样本；Pe（·）为第e台运行风电机组的风电转换函数，该函数由风电机组的切入风速、额定风速、切出风速和额定容量构成，详细公式参考文献［16］。

4）结合常规机组的启停状态，求出所有常规机组的可用容量PG，如式（9）所示。

式中：Gf为第f台运行常规机组的额定容量；NG为运行常规机组的数量。

5）利用PWF、PG和系统年负荷，计算每个抽样年q的失电次数η（LLO，q）、失电持续时间η（LLD，q）和失电量η（ENS，q）。

6）当仿真至Q年度后，计算系统充裕度指标：期望失电持续时间βLOLE、期望失电频率βLOLF、期望失电量βLOEE，具体表达式如附录A式（A3）—（A5）所示。

7）循环步骤2）—6），直到βLOEE的方差系数小于0.02 或Q大于最大仿真时间，结束循环，得到3 类充裕度指标结果。

2.3 风电容量可信度评估

在2.2节充裕度评估的基础上，以某类充裕度指标为基准，在等可靠性准则下利用等效固定容量的衡量标准，以新并入的风电机组容量所能替换的理想常规机组容量作为风电可信容量CE，则装机容量为Cwind的风电容量可信度ζ［17］为：

本文采用文献［18］中的弦截法计算风电容量可信度，该方法具有计算复杂度低、收敛速度快等优点。

3 算例分析

3.1 风速云模型的验证

基于美国北达科他州农业气象网络（North Dakota agricultural weather network，NDAWN）Prosper观测站2011 — 2020年每小时实测的风速样本［19］，利用ARMA 模型、混合半云模型和本文基于互Box-Cox变换和Markov 链的风速云模型仿真该观测站的实测风速样本。

在应用本文模型时，通过极大似然估计法求得λ= 0.353，利用Box-Cox 变换将实测风速样本变换为实测云滴样本，并计算出实测云滴样本的EX、EN、HE分别为1.648、1.012、0.167。为确定实测云滴样本等分区间数，分别取区间数K= 5，10，15，20，25，比较不同区间数下本文仿真风速样本的分布特征。表1 为不同模型风速样本的统计指标，可以得出如下结论。

表1 不同模型风速样本的统计指标Table 1 Statistical indicators of wind speed samples for different models

1）当K取不同值时，本文模型仿真风速样本的4 种统计指标与实测风速样本的4 种统计指标相差较小，这表明实测云滴样本等分区间数对本文仿真风速样本的分布特征影响较小。

2）相较于ARMA 模型和混合半云模型，本文模型的仿真风速样本在各区间数下的均值、标准差与实测风速样本的均值、标准差更接近，这表明本文模型仿真风速样本的分布特征与实测风速样本的分布特征具有良好的相似性。

3）通过观察各风速样本的变化区间可知，ARMA模型和混合半云模型的仿真风速样本变化区间与实测风速样本变化区间相差较大，且产生了负值仿真风速样本，而5 种区间数下本文模型的仿真风速样本在保证非负性的同时，能与实测风速样本的变化区间保持较高的一致性。

图3 为不同模型风速样本在滞后15 h 内的自相关系数曲线，可以得出如下结论。

图3 不同模型风速样本的自相关系数曲线Fig.3 Autocorrelation coefficient curves of wind speed samples for different models

1）当区间数K=5 时，本文模型仿真风速样本的自相关系数曲线与实测风速样本的自相关系数曲线贴合较差，在增加区间数后，该贴合程度有所改善，采用均方根误差［20］衡量不同区间数下仿真风速样本的自相关系数与实测风速样本的自相关系数在滞后15 h内的误差，得到区间数K为5、10、15、20、25时的均方根误差分别为0.042、0.013、0.025、0.031、0.034。可见，K=10 时的均方根误差最低，这表明该区间数下本文模型仿真风速样本的自相关系数曲线更贴近于实测风速样本的自相关系数曲线，因此，选取K=10作为本文模型实测云滴样本等分的区间数。

2）随着时间的不断推移，混合半云模型仿真风速样本的自相关系数始终位于0 附近，这表明混合半云模型的仿真风速样本之间基本无自相关性。

3）ARMA 模型仿真风速样本的自相关系数曲线与实测风速样本的自相关系数曲线较为接近，而本文模型（K=10）仿真风速样本的自相关系数曲线虽然与实测风速样本的自相关系数曲线存在一定差距，但整体上呈现出与实测风速样本类似的变化趋势，即随着时间的不断推移，仿真风速样本自相关系数曲线呈现指数衰减的变化趋势。

实测云滴样本在10组云滴区间内转移率矩阵P的计算结果如附录B表B1所示。

为进一步验证本文模型的准确性，结合表1 中实测风速样本以及ARMA模型、混合半云模型、本文模型（K=10）仿真风速样本的最小值和最大值，将3 个仿真风速样本变化区间按每段区间长度为1.5 m／s 进行分段，不同模型风速样本的频率分布直方图如图4 所示。由图可知，相较于ARMA 模型和混合半云模型的仿真风速样本，本文模型的仿真风速样本能够更准确地描述实测风速样本在大多区间内的分布情况。假设DARMA、DH、DBCM分别为ARMA模型、混合半云模型、本文模型仿真风速样本与实测风速样本间的巴氏距离［21］，巴氏距离越小，则仿真风速样本与实测风速样本的概率分布特征越相似，可 得DARMA、DH、DBCM分别为3.473×10-2、2.593×10-3、1.784×10-5，可见，DBCM小于DARMA和DH，这表明从巴氏距离的角度，本文模型仿真风速样本的概率分布与实测风速样本的概率分布更接近。

图4 不同模型风速样本的频率分布直方图Fig.4 Frequency distribution histogram of wind speed samples for different models

上述分析验证了本文模型可较精确地计及Prosper 观测站实测风速样本的随机性，而对于风速自相关性，虽然本文模型与ARMA 模型存在一定差距，但在综合考虑风速随机性和自相关性时，本文模型具有更高的仿真精度。

3.2 含风能IEEE-RTS发电系统的充裕度评估

原IEEE-RTS 发电系统包含32 台常规机组，总装机容量为3 405 MW，峰值负荷为2 850 MW，常规机组和负荷的详细数据参考文献［22］。原IEEE-RTS发电系统的βLOLE、βLOEE、βLOLF分别为9.371 6 h／a、1 197.444 8 MW·h／a和1.919 2 次／a［22］。

假设Prosper 观测站内建有200 台同型号的风电机组，其切入风速、切出风速和额定风速分别为3、15、8 m／s，故障率、额定功率和修复时间分别为2 次／a、1.5 MW 和480 h／次，因此该观测站的风电总装机容量为300 MW。将该观测站的风电场并入原IEEE-RTS 发电系统，并根据2.2 节的充裕度评估步骤评估含风能IEEE-RTS发电系统的充裕度指标，结果如表2 所示，表中误差为相应模型充裕度指标相对于实测风速样本充裕度指标的误差，可以得出如下结论。

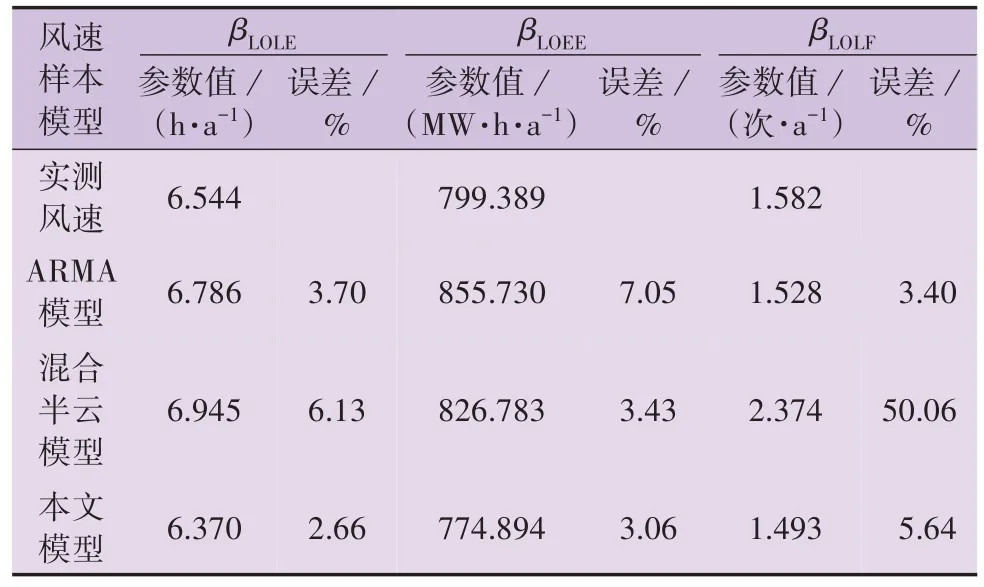
表2 Prosper观测站不同模型的充裕度指标Table 2 Adequacy indicators of different models at Prosper observatory

1）相较于原IEEE-RTS发电系统的充裕度指标，风电场并网后的3 类充裕度指标均明显降低，这表明风电场并网对电力系统充裕度有一定的改善作用。

2）本文模型充裕度指标的误差最大值为5.64 %，而ARMA模型和混合半云模型充裕度指标的误差最大值分别为7.05 % 和50.06 %，这表明本文模型充裕度指标更接近实测风速样本的充裕度指标。另外，混合半云模型评估得到的βLOLF的相对误差为50.06 %，而本文模型评估得到的βLOLF的相对误差仅为5.64 %，这表明βLOLF对仿真风速样本自相关性的敏感程度较高。

综上，本文模型可较精确地评估Prosper 观测站含风能IEEE-RTS发电系统的充裕度。另外，若风速仿真模型忽视实测风速样本的自相关性，则将导致各项充裕度指标产生较大误差，特别是βLOLF，βLOLF对仿真风速样本自相关性的敏感程度高于βLOLE和βLOEE。

3.3 风电容量可信度评估

在3.2 节充裕度评估的基础上，本文以βLOLE、βLOEE、βLOLF这3 类充裕度指标为基准，根据等效固定容量的基本思想，采用弦截法计算Prosper 观测站的风电容量可信度。表3为Prosper观测站不同模型在3 类充裕度指标下的风电容量可信度，可以得出如下结论。

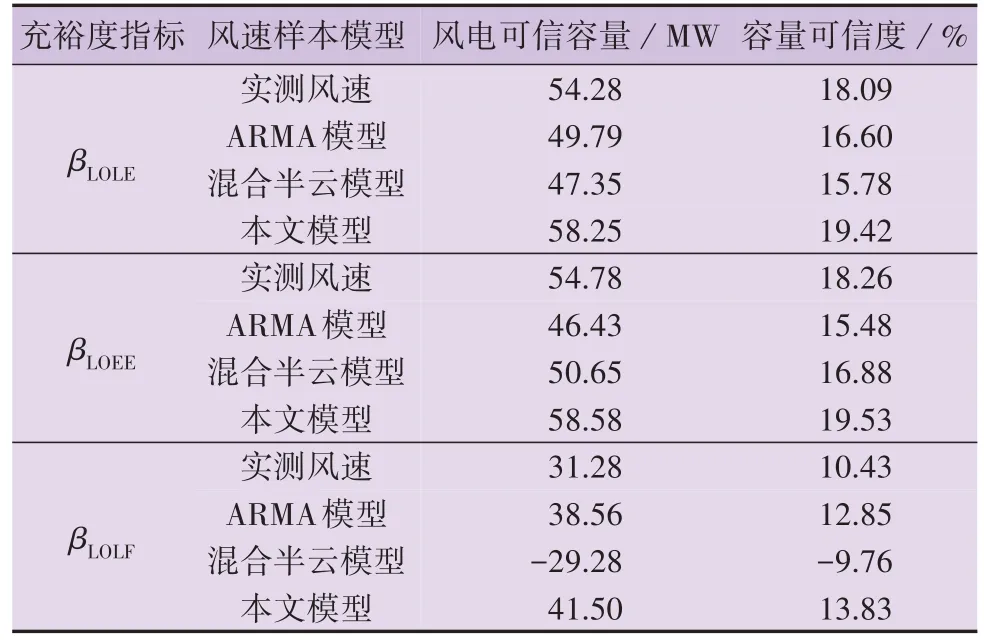
表3 Prosper观测站不同模型在3类充裕度指标下的风电容量可信度Table 3 Capacity credit of different models under three adequacy indicators at Prosper observatory

1）以βLOLE和βLOEE为基准时，本文模型评估的风电容量可信度更接近实测风速样本的评估结果，而ARMA 模型和混合半云模型的评估结果与实测风速样本的评估结果差距较大，且均低估了风电容量可信度。

2）以βLOLF为基准时，混合半云模型评估的风电容量可信度为负值，这说明风电场对电力系统可靠运行有负面影响，与实际情况相悖，忽视风速自相关性的混合半云模型不适用于评估以βLOLF为基准的风电容量可信度。另外，相较于混合半云模型的评估结果，ARMA 模型和本文模型的评估结果更接近实测风速样本的评估结果。

综上，在评估风电容量可信度时，ARMA 模型与本文模型具有较高的准确性，但综合3 类充裕度指标下的评估结果可知，本文模型具有更优的适用性和准确性。

3.4 风能资源对充裕度评估的影响

为研究风能资源对充裕度评估的影响，本文收集Crary 和Berthold 观 测 站2011 — 2020 年 每 小 时 的实测风速样本［19］。利用ARMA 模型、混合半云模型和本文模型仿真Crary和Berthold观测站的实测风速样本，以验证本文模型能较精确地计及不同观测站实测风速样本的概率分布特性和自相关性，对比结果如附录B图B1 — B4所示。

Crary 和Berthold 观测站实测风速样本的统计指标如附录B 表B2 所示。由表可知，相较于Crary 观测站，Berthold观测站具有更加充沛的风能资源。

假设在Crary 和Berthold 观测站内建有200 台同型号的风电机组，其各项参数与前文保持一致。利用实测风速样本、ARMA 模型、混合半云模型和本文模型对含风能IEEE-RTS 发电系统的充裕度进行评估，结果如附录B表B3所示，可以得出如下结论。

1）对于风能资源更丰富的Berthold 观测站，其风电并网系统的充裕度更高，这表明风能资源越丰富的观测站，其风电并网对电力系统充裕度的改善效果越明显。

2）对于Crary 和Berthold 观测站，相较于ARMA模型和混合半云模型，本文模型的充裕度评估结果与实测风速样本的充裕度评估结果更接近，误差最大值为4.31 %，而ARMA 模型和混合半云模型充裕度指标的误差最大值分别为7.62 % 和77.42 %，这表明本文模型可较精确地评估不同观测站处风电并网系统的充裕度。

3）对于Crary 和Berthold 观测站，混合半云模型的充裕度指标误差在3.94 %～77.42 % 的较大范围内波动，而本文模型可将该误差降低至1.17 %～4.31 %。其中，混合半云模型在Crary 观测站的βLOLF误差为68.18 %，而在Berthold观测站的βLOLF误差为77.42 %，这说明当使用忽视风速自相关性的混合半云模型评估风能资源更丰富的观测站的βLOLF时，评估结果误差也会增大。因此，若风速仿真模型忽视实测风速样本的自相关性，则βLOLF误差将随着风能资源的丰富程度逐渐增大。

4 结论

本文提出基于互Box-Cox 变换和Markov 链的风速云模型，并将该模型与时序Monte Carlo 模拟法结合，提出风电并网系统充裕度评估方法。利用ARMA 模型、混合半云模型和本文模型仿真美国北达科他州某处观测站的实测风速样本，评估风电并网系统的充裕度和风电容量可信度，并分析不同风能资源对充裕度评估结果的影响，得出以下主要结论：

1）本文模型能克服混合半云模型产生负值仿真风速样本和未充分计及实测风速样本自相关性的不足，算例分析验证结果表明，本文模型可较精确地计及实测风速样本的随机性和自相关性；

2）在评估3 类充裕度指标下的风电容量可信度时，本文模型具有良好的适用性和较高的准确性。

3）风电场并网对电力系统的充裕度有一定的改善作用，当风能资源更充沛时，改善效果将会进一步增强，此时若使用忽视风速自相关性的风速仿真模型评估βLOLF，则将导致其评估结果误差增大。

笔者后续将结合本文模型与Copula 模型，计及多座风电场风速的互相关性，以评估含多座风电场发电系统的充裕度。

附录见本刊网络版（http：//www.epae.cn）。