直升机设备安装平台的强度优化设计

杨林河 钱学森 张运来

摘  要：该文以直升机设备安装平台为研究对象，应用MSC Patran/Nastran软件，对平台承受最严重过载工况下的最大应力和屈曲失稳系数进行分析，得出各因素对最大应力和屈曲失稳系数的影响。之后通过OptiStruct对平台构型进行拓扑优化，确定平台最终构型。

关键词：设备安装平台；有限元方法；拓扑优化；筋条；稳定性

中图分类号：V243      文献标志码：A         文章编号：2095-2945（2024）08-0020-04

Abstract： Taking the helicopter equipment installation platform as the research object， this paper analyzes the maximum stress and buckling instability coefficient of the helicopter equipment installation platform under the most serious overload condition by using MSC Patran/Nastran software， and obtains the influence of various factors on the maximum stress and buckling instability coefficient. After that， the topology of the platform is optimized by OptiStruct to determine the final configuration of the platform.

Keywords： equipment installation platform; finite element method; topology optimization; ribs; stability

隨着科技的不断进步和航空工业的发展，直升机上各产品结构不仅要安全、稳定，还要轻量化、低成本。设备安装平台是直升机上常见的结构形式，在其上设备各方向的过载下，设备安装平台的承载能力和稳定性直接关系到安装设备安全与否。直接用试验验证结构强度性能耗时耗力，而运用有限元方法对结构进行仿真计算是工程上的常见手段。范学伟[1]和霍健[2]基于有限元计算分别对直升机雷达平台和隔振平台进行设计研究。闫华卓[3]和邹赛等[4]运用有限元软件分别对海上风电安装平台和柴油机安装平台进行了总强度和结构失稳分析。目前，有限元软件众多，而MSC Patran/Nastran软件因其具备可靠、高效、支持多工况计算等优点被广泛应用在航空领域，本文也将对其进行结构强度计算。

产品设计应当在满足强度刚度等要求的同时，尽可能地设计出轻重量比的结构。拓扑优化可以在不降低结构性能的前提下确定结构最佳分布形式，从而减少结构重量。在商业优化软件中，Optistruct被广泛应用在各大行业。刘伟等[5]和何成龙等[6]基于Optistruct分别对机身前段和重力坝进行了总体优化设计。葛东东等[7]应用Optistruct对汽车骨架进行了优化设计，从而使骨架质量减轻18.96%。

本文以直升机设备安装平台为研究对象，应用有限元软件MSC Patran/Nastran对承受最严重过载工况下的平台结构进行仿真计算，分析多个因素对最大应力和屈曲失稳系数的影响。再应用Optistruct中的topology模块对平台结构进行拓扑优化，确定平台最终构型。

1  初始方案

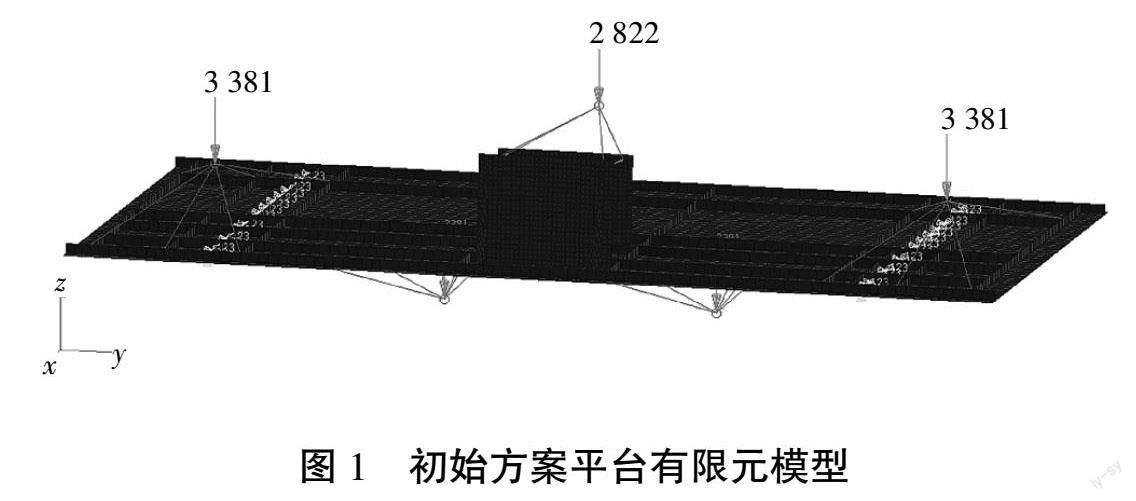
根据结构数模，建立有限元模型如图1所示。其中，平台底板、筋条采用shell单元模拟，安装设备通过RBE3模拟，采用Fastener单元模拟铆钉连接。在平台螺栓连接处约束123平动自由度。

初始方案中，筋条高度H为20 mm，筋条厚度T1为2 mm，平台底板厚度T2为1.5 mm。所有材料均为铝合金，弹性模量取71 GPa，泊松比取0.33，密度取2.8×10-6 kg/mm3。

初始方案计算结果如图2和图3所示。由图2和图3可知，平台最大应力为1 620 MPa，屈曲因子为0.125 95。对铝合金材料，许用应力一般取390 MPa；屈曲分析中，结构屈曲因子大于1，才能确保结构不发生失稳。故初始方案不满足强度条件。

2  影响因素分析

针对初始方案不满足材料应力和稳定性要求，本节将研究筋条高度H、筋条厚度T1，以及平台底板厚度T2对平台最大应力和屈曲因子的影响情况。

2.1  筋条高度H的影响

在其他条件相同时，分别取筋条高度H=20、30、40 mm，研究筋条高度H对平台最大应力和屈曲因子的影响情况。

图4和图5为平台底板厚度T2为2 mm，筋条厚度T1分别为1、2、3 和4 mm时，平台最大应力和屈曲因子随筋条高度的变化图。

由图4可知，平台最大应力随着筋条高度的增大而减小。在筋条厚度分别为1、2、3和4 mm时，当筋条高度H从20 mm增加到30 mm和从30 mm增加到40 mm时，最大应力下降幅度分别从1 510 MPa到了610 MPa，从825 MPa下降到了284 MPa，从559  MPa下降到了209  MPa，从420  MPa下降到了128  MPa。由此可见，筋条高度H在20～30 mm时，筋条高度对最大应力的作用明显；在30～40 mm时下降幅度均逐渐减小，曲线也逐渐平缓。

由图5可知，平台屈曲因子基本趋势是随着筋条高度的增大而增大。在筋条厚度分别为1、2、3和4 mm时，当筋条高度H从20 mm增加到40 mm时，屈曲因子增加幅度分别为0.01、0.36、1.11和1.99。很明显，屈曲因子不仅受筋条高度的影响，筋条厚度对屈曲因子的影响也较大，两者对屈曲因子的影响会共同作用，下一节将讨论筋条厚度对屈曲因子的影响。

2.2  筋條厚度的影响

在其他条件相同时，分别取筋条厚度T1=1、2、3、4 mm，研究筋条厚度T1对平台最大应力和屈曲因子的影响情况。

图6和图7为平台底板厚度T2为2.5 mm，筋条高度H分别为20、30 、40 mm时，平台最大应力和屈曲因子随筋条厚度的变化图。

由图6可知，平台最大应力随着筋条厚度的增大而减小。在筋条高度分别为20、30、40 mm时，当筋条厚度T1从1 mm增加到2 mm和从3 mm增加到4 mm时，最大应力下降幅度分别从1 400 MPa到了249 MPa，从828 MPa下降到了119 MPa，从521 MPa下降到了77 MPa。由此可和，下降幅度均逐渐减小，曲线也逐渐平缓。

由图7可知，平台屈曲因子是随着筋条厚度的增大而增大。在筋条高度分别为20、30、40 mm时，当筋条厚度T1从1 mm增加到2 mm，屈曲因子增加幅度分别为0.07、0.46、0.47；但当筋条厚度T1从3 mm增加到4 mm时，屈曲因子增加幅度分别为0.09、0.29、1.49。由此可知，筋条厚度T1在大于3 mm时，其对屈曲因子的作用更明显。

2.3  底板厚度的影响

在其他条件相同时，分别取平台底板厚度T2=1.5、2.0、2.5 mm，研究平台底板厚度T2对平台最大应力和屈曲因子的影响情况。

图8和图9为筋条高度H为40 mm，筋条厚度T1分别为1、2、3和4 mm时，平台最大应力和屈曲因子随底板厚度的变化图。

由图8可知，平台最大应力随着底板厚度的增大而减小，且下降幅度均逐渐减小，曲线也逐渐平缓。同时，也可以看出，在此状态下，筋条厚度T1为1～2 mm比T1为3～4 mm的平台最大应力下降幅度大许多。

由图9可知，平台屈曲因子随着筋条厚度的增大而增大。在筋条厚度分别为1、2、3和4 mm时，当底板厚度T2从1.5 mm增加到2.5 mm时，屈曲因子增加幅度分别为0.006、0.121、0.589和2.004。可见，随着筋条厚度的增大，屈曲因子随着底板厚度的增大而增大得更明显。

3  拓扑优化

以筋条高度H为40 mm，筋条厚度T1为3 mm，平台底板厚度T2为2.0 mm的平台为研究对象进行拓扑优化，平台重量为19.2 kg。将底板和筋条取为设计区，材料的厚度为设计变量，体积分数最小为目标函数，结构的柔度为约束条件，优化计算获得最佳的结构材料分布形式。再基于拓扑优化结果对平台结构重新设计，减轻重量，确定平台最终构型。

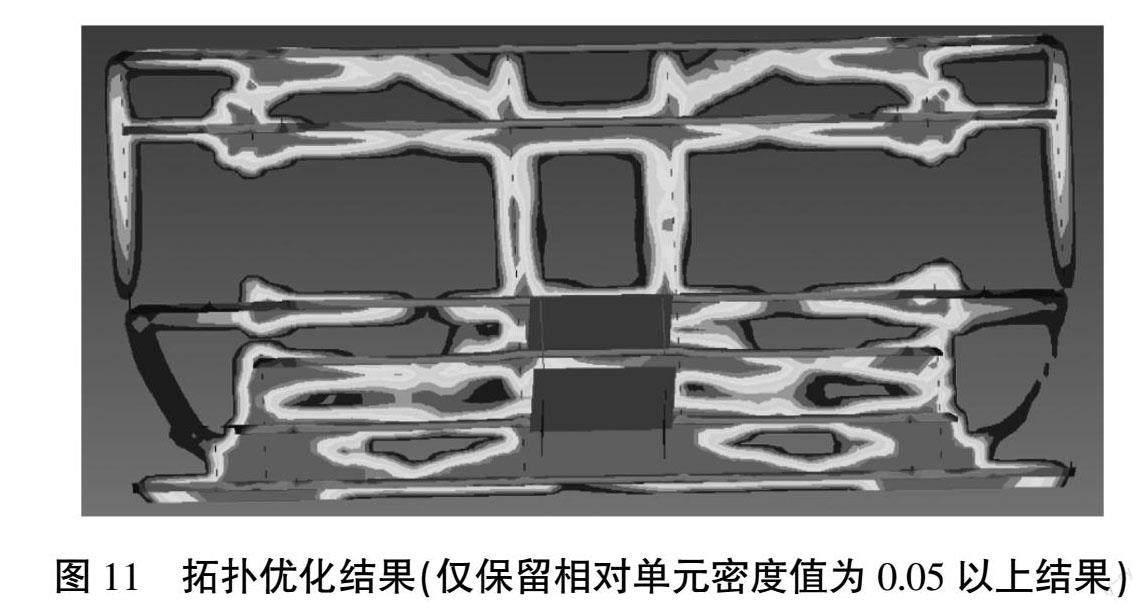
拓扑优化结果如图10和图11所示。图中结果代表单元的相对密度值，其数值趋向于l（灰色）时，表示该区域材料越要保留；数值趋向于0（黑色）时，表示该区域材料可以删除[8]。

依据拓扑优化结果，结合实际情况，对平台结构进行重新设计，最终构型的最大应力云图和屈曲因子分别如图12和图13所示。

由图12和图13可知，平台最终构型最大应力为308 MPa，小于许用应力390 MPa；屈曲因子为1.312，大于临界屈曲因子1。故平台最终构型满足强度条件。平台最终构型重量为15.4 kg，相比于未优化前，平台在优化后减重19.8%。

4  结论

本文以直升机设备安装平台为研究对象，通过有限元计算结果分析了各因素对平台最大应力和屈曲失稳系数的影响。再应用Optistruct软件对平台结构进行拓扑优化，确定了平台最终构型。主要得出结论如下：

1）平台最大应力随着筋条高度H、筋条厚度T1及平台底板厚度T2的增大而减小；

2）平台屈曲因子随着筋条高度H、筋条厚度T1及平台底板厚度T2的增大而增大。

3）依据拓扑优化结果确定的平台最终构型方案可行，满足强度条件，且优化后平台减重19.8%。

参考文献：

[1] 范学伟.基于有限元计算及动力学试验的某型直升机雷达平台结构优化[J].中国科技纵横，2020（2）：54-55.

[2] 霍健.一种直升机机载跟瞄系统被动隔振平台设计[D].秦皇岛：燕山大学，2021.

[3] 闫华卓.96 m海上风电安装平台总强度分析[D].镇江：江苏科技大学，2019.

[4] 邹赛，翁晓杰.某柴油机EGR安装平台结构失稳分析[J].内燃机与配件，2019（24）：46-48.

[5] 刘伟，张志斌，刘清颖，等.基于OptiStruct的机身前段总体优化设计[J].机械设计与研究，2013，29（5）：30-33.

[6] 何成龙，涂兴怀.基于Optistruct的重力坝拓扑优化应用研究[J].水力发电，2013，39（10）：37-40.

[7] 葛东东，祝良荣，玄东吉，等.基于OptiStruct的电动汽车车身骨架拓扑优化[J].科技通报，2015（9）：240-244.

[8] 苏胜伟.基于Optistruct拓扑优化的应用研究[D].哈尔滨：哈尔滨工程大学，2008.