极地半潜式海洋平台在不同环境载荷下的动态响应分析
2024-03-22张奥博闯振菊刘社文李春郑季顺迎
张奥博,闯振菊,刘社文,李春郑,季顺迎,屈 衍
(1.大连海事大学船舶与海洋工程学院,辽宁大连 116026;2.上海勘探设计研究院有限公司,上海 200335;3.大连理工大学工业装备结构分析国家重点实验室,辽宁大连 116024;4.华南理工大学海洋科学与工程学院,广州 511442)
0 引 言
全球变暖的现象加剧了北极地区的冰雪融化,也为北极油气资源的开采创造了条件。2008年,美国地质调查局完成了对北极圈以北所有地区未发现的常规油气资源的评估。报告推断出北极未发现的常规油气资源平均储量约为900 亿桶石油、1669 亿万立方英尺天然气和440 亿桶液化天然气。其中,大约84%未被发现的油气资源位于海上[1]。然而,在北极地区进行石油勘探是非常困难的,难点在于大量未发现的石油储存在水深大于100 米[2]且小于500 米[3]的水域,再加上海冰对结构物的影响,极地油气资源的开采并未成为常态。在极地进行海上作业的平台需要考虑作业水深、可变载荷、抗冰能力、恶劣环境的适应能力等多种因素[4]。半潜式海洋平台因为其较好的运动性能和能够适应深水作业的特点被看作是在极地开采油气资源的最佳方案。
当前学术界对波浪载荷作用下海洋平台的研究取得了很多成果。刘海霞和肖熙[5]得出了对于小结构物,波浪的拖曳力和惯性力是主要分量,对于大结构物,波浪的惯性力和绕射力是主要分量。大型半潜式平台的波浪载荷计算采用Morison 公式和势流理论相结合的方法;张威等[6]分别采用频域分析法与时域分析法对南海某深水半潜式平台的运动响应进行了计算,对比分析了两种方法在深水半潜式平台运动响应预报结果上的异同;宋安科[7]对第五代半潜式钻井平台进行了水动力分析,并对系泊系统和平台进行了静力分析和时域耦合动力分析,得到了平台运动位移和系泊线张力的时历响应曲线。
国内外众多学者对海冰与平台的相互作用已开展了深入的分析。挪威科技大学Hansen和Loset[8]采用二维圆盘单元对破碎冰场在外力作用下的运动学和动力学进行了模拟,并对定位在碎冰区的海洋结构物进行了分析;Zhou 等[9]建立了一种二维数值模型来模拟平整冰和锚泊结构相互作用的过程,应用船舶冰阻力的半经验公式模拟了冰的旋转和滑动过程,数值模拟的结果通过与Wright[10]的实测数据进行对比得到了验证;刘璐等[11]基于闵可夫斯基原理的扩展多面体离散元方法模拟船舶与海洋平台结构的相互作用过程,采用离散元方法分析了船舶结构绕行过程中的船舶和海洋平台结构冰载荷。
一些学者对海洋平台的抗冰性能也进行了研究。张帅[12]通过数值模拟计算了圆柱及两种抗冰形状结构的波浪载荷,讨论了这两种结构在无冰期对海洋平台桩腿的影响;龙雪等[13]采用具有粘结破碎功能的离散元方法计算海冰与锥体作用的破坏过程,将离散元计算冰载荷及海冰破坏模式与渤海现场实测数据进行对比验证,得出倒锥体结构可有效降低冰载荷从而具有较好的抗冰性能;张大勇等[14]对典型半潜式平台与海冰相互作用机理和冰载荷模型进行分析,提出了该类结构在海冰作用下的主要失效模式及评价方法。
海洋平台在极地进行海上作业的过程中需要进行海冰管理。本研究的主要目的是研究半潜式生产平台在北极有冰和无冰时的动态响应,包括海冰管理前的平整冰工况以及海冰管理后的碎冰工况。通过时域模拟,研究平台在波浪荷载和冰荷载作用下的运动、锚链张力的变化规律,并对不同工况的影响加以分析。
1 数值模型介绍
本文选用的半潜式海洋平台如图1 所示,主要由包括钻井设备和生活区等大多数功能模块的上部结构、提供浮力的浮筒、四根连接浮筒和上层甲板的立柱以及立柱间的横撑组成。平台的更多信息可参照表1。

表1 平台的基本设计参数Tab.1 Basic design parameters of the platform
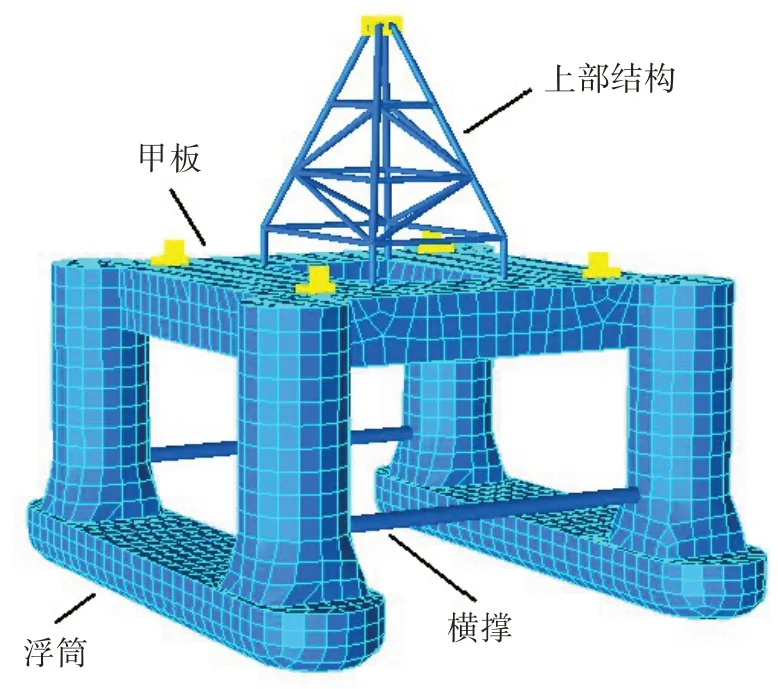
图1 半潜式海洋平台Fig.1 Semi-submersible offshore platform
数值模型中的锚泊系统包括12 根锚链及22 根立管,与半潜式海洋平台构成一个耦合的整体。平台的运动会影响锚链的受力。朝着不同方向呈放射型布置的锚链可以提供给平台回复力和力矩,抵抗外部载荷以保证平台可以正常作业。锚泊系统的具体布置及外部载荷的入射角度如图2 所示(M 表示锚链,R 表示立管),锚链和生产立管的具体情况见表2。

表2 锚链和生产立管的基本信息Tab.2 Basic information of the mooring lines and the production risers

图2 锚泊系统的排列形式及外部载荷的入射方向Fig.2 Arrangement of the mooring system and the incident direction of external loads
2 理论方法介绍
2.1 波浪荷载分析
本文采用势流理论[15]和Morison理论[16]来计算分析波浪荷载。平台的水动力特性分析以及结构运动响应计算是基于SESAM 软件[17]来完成的。WADAM 模块[18]可以用来进行波浪载荷下的频域响应分析,通过计算得到一阶波浪力和二阶波浪力的传递函数。SIMA 模块[19-20]可以用来进行平台与锚泊系统耦合下的时域响应分析,通过计算不同工况下平台的运动以及锚泊系统的受力,得到整体的运动响应特性。
在研究半潜式海洋平台的运动时,忽略它的柔性变形,将其看作刚体,主要分析平台六自由度的运动情况。OXY平面与静止的水面重合,OZ轴垂直于水面,指向上方。
根据势流理论,可以得到半潜式海洋平台在频域下的一阶运动方程为
式中,Mij为质量矩阵,μij为附加质量矩阵,λij为阻尼系数矩阵,Cij为回复力系数矩阵,Xj为平台的运动,Fi为平台所受到的一阶波浪力。
Morison方程主要分为两个部分,分别是拖曳力计算和惯性力计算。Morison方程的表达式为
式中,FD表示拖曳力,FI表示惯性力。
线性的一阶波浪力是通过将速度势分解为入射势、绕射势和辐射势,利用伯努利方程求得。二阶波浪力对系泊系统的运动有着重要的影响,因为平台在波浪的作用下会产生漂移。平均漂移力是一个非线性的二阶力,计算时采用远场法[21]和压力积分法[22]。文中选择的半潜式海洋平台是双对称结构,波浪方向选为0°~90°,间隔为15°。传递函数计算周期为4~38 s,步长为2 s。
2.2 冰荷载分析
本文采用离散元[23]的方法来分析冰荷载。该方法可以模拟冰从完整状态到破裂状态的整个过程[24],从而分析海冰的破坏模式以及冰载荷的大小。在离散元的方法中,海冰颗粒间的相互作用采用了基于莫尔-库仑剪切摩擦定律的弹性-粘性接触模型[25]来确定。该方法采用了平行粘结模型将球形颗粒结合成平整冰。平行粘结模型中的两个粘结颗粒单元间设定一个弹性粘结圆盘,这样的模型既能传递力又能传递力矩[26]。
平行粘结模型的基本情况如图3所示。在平行粘结模型中,--→-Fni和--→-Fsi分别为颗粒间的法向力和切向力,-- →-Mni和-- →-MSi分别为颗粒间的法向力矩和切向力矩,作用在粘结圆盘上的最大正应力和最大剪应力[24]可分别表示为
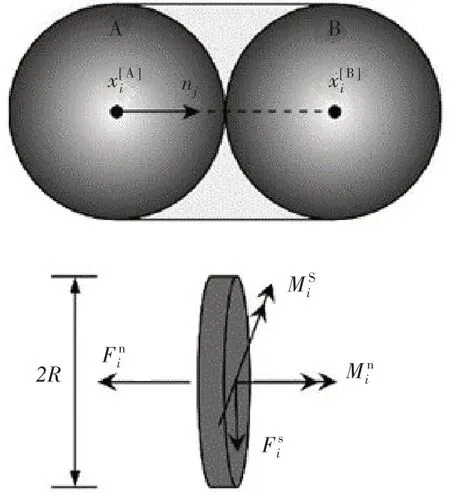
图3 球体单元的平行粘结模型[24]Fig.3 Parallel bonding model for spherical elements
式中,R为粘结圆盘的半径、A为粘结圆盘的横截面积、I和J分别为粘结圆盘的惯性矩与极惯性矩。具体计算可表示为
判断平行粘结圆盘的破坏失效采用了断裂准则。在模拟海冰的断裂过程中,可以通过颗粒单元的法向和切向受力状态将单元之间的粘结失效方式分为拉伸破坏和剪切破坏[27],如图4所示。当粘结圆盘的最大正应力σmax超过颗粒单元之间的拉伸破坏强度σt,或者最大剪应力τmax超过颗粒单元间的剪切破坏强度τs时,粘结圆盘会失效。

图4 颗粒单元的粘结失效模型[25]Fig.4 Bonding failure model of particle element
碎冰区的构建是基于二维Voronoi 图的切割算法来完成的。采用二维Voronoi 图可以将碎冰区域快速划分为不规则的多边形集合。在此基础上,按照一定比例调整各个多边形的尺寸以生成碎冰区的平面几何模型,由此通过切割球体单元构造的平整冰即可得到碎冰块的离散元模型[28]。此方法可以对不同海冰厚度、海冰密集度和冰块平均面积下的碎冰区进行模拟,从而进行离散元计算。
用离散元方法模拟海冰所需要的主要参数[29]如表3所示。

表3 海冰离散元计算的主要参数Tab.3 Main parameters of sea ice discrete element calculation
本文将综合比较半潜式海洋平台在波浪载荷和冰载荷(包括平整冰和碎冰)下六个自由度的运动和锚链的受力,图5给出了数值研究的流程。

图5 计算流程图Fig.5 Roadmap of load calculation
2.3 模型的网格收敛性分析
网格的收敛性分析是为了验证不同的网格数目对计算结果产生的影响。本文选用了三组不同的模型进行频域下水动力性能的计算和分析。这三组不同的模型是基于水下平均湿表面在纵向和周向显示不同的网格来创建的,三组网格模型的具体信息如表4所示。

表4 三种模型的网格收敛研究Tab.4 Study on mesh convergenceof three models
本文通过对比三组网格模型的平台运动幅值响应算子RAO、平台受到的一阶波浪力以及二阶平均漂移力来验证网格的收敛性。图6~7为4~38 s的计算周期内平台纵荡、纵摇的一阶运动传递函数;图8~9 为平台受到的一阶波浪力;图10~12 为在远场法和压力积分法的计算下得到的平台二阶平均漂移力。

图6 30°波浪方向的一阶纵荡运动幅值响应算子Fig.6 First-order surge motion RAO with wave direction 30°
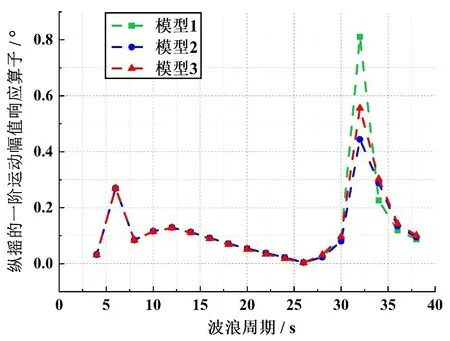
图7 75°波浪方向的一阶纵摇运动幅值响应算子Fig.7 First-order pitch motion RAO with wave direction 75°

图8 45°波浪方向的纵荡一阶波浪力Fig.8 First-order surge force with wave direction 45°
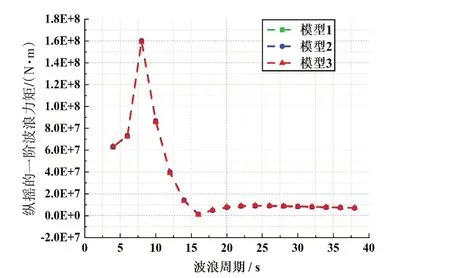
图9 0°波浪方向的纵摇一阶波浪力矩Fig.9 First-order pitch moment with wave direction 0°

图10 0°波浪方向的纵荡二阶平均漂移力Fig.10 Second-order surge mean drift force with wave direction 0°

图11 30°波浪方向的横荡二阶平均漂移力Fig.11 Second-order sway mean drift force with wave direction 30°

图12 60°波浪方向的艏摇二阶平均漂移力矩Fig.12 Second-order yaw mean drift force with wave direction 60°
从图中可以看出,三组模型的一阶波浪力和二阶平均漂移力几乎一致,平台在纵荡、垂荡以及纵摇方向上的一阶运动幅值响应算子RAO略有偏差。模型3在存在偏差处的数据更接近三组模型数据的平均值,而且此模型的网格最精细。考虑到计算精度,本文最终选定模型3(如图13)作为后续的网格模型。

图13 网格计算模型Fig.13 Mesh of calculation model
3 数值计算与结果分析
3.1 计算工况介绍
本文选定了坐标在北纬60°~70°、西经45°~60°的格陵兰海域作为研究对象。格陵兰海域的气象条件、海洋情况以及海冰条件都可以在ISO 19906(2010)规范[30]中找到。具体数据如表5所示。

表5 格陵兰海域的环境情况Tab.5 Environmental conditions in the Greenland Sea
本文需要分别对比波浪载荷和冰载荷作用下锚链的拉力变化以及海洋平台的运动响应。不同环境载荷下平台和锚泊系统的相关数据都能在SIMA 中计算得到。根据格陵兰海域的环境情况,最终确定4 组波浪作用下的工况、8 组平整冰作用下的工况以及9 组碎冰作用下的工况,具体情况如表6~8 所示。波浪和海冰的入射方向均为180°。碎冰的速度与该海域水的流速一致,确定为1 m/s,计算碎冰时不考虑波浪的影响。波浪载荷的不同工况是通过有义波高和谱峰周期加以区分的;平整冰的影响因素包括冰厚和冰速,计算区域为2000 m×200 m;碎冰的变量分别为海冰厚度、海冰密集度和冰块平均面积,计算区域为4000 m×200 m。图14~19展示了不同密集度和平均面积下的碎冰场。

表6 波浪工况Tab.6 Wave conditions

表7 平整冰工况Tab.7 Level ice conditions

表8 碎冰工况Tab.8 Ice floe conditions

图14 80%密集度、平均面积20 m2的碎冰区Fig.14 Broken ice field of 80%concentration and 20 m2 mean area

图16 80%密集度、平均面积100 m2的碎冰区Fig.16 Broken ice field of 80%concentration and 100 m2 mean area

图17 60%密集度、平均面积50 m2的碎冰区Fig.17 Broken ice field of 60%concentration and 50 m2 mean area

图18 40%密集度、平均面积50 m2的碎冰区Fig.18 Broken ice field of 40%concentration and 50 m2 mean area

图19 20%密集度、平均面积50 m2的碎冰区Fig.19 Broken ice field of 20%concentration and 50 m2 mean area.
3.2 环境载荷对平台系统的的影响分析
图20 展示了在不同波浪载荷的作用下,5 号锚链受到拉力的最大值、最小值和平均值。选取5 号锚链是因为在180°外部载荷的作用下,5号锚链始终处于张紧状态,比较具有代表性。从图中可知,随着有义波高和谱峰周期的增加,锚链受到的最大拉力也随之变大。工况4 下锚链受到的最大拉力比工况1、工况2、工况3分别增大了55.6%、39.0%、13.2%。

图20 波浪工况下5号锚链的拉力Fig.20 Tension of No.5 mooring line under wave conditions
讨论平整冰的影响因素可以参考图21,从图中可以看出不同冰厚和冰速下产生的差异,海冰厚度的影响相较于海冰速度更明显。冰的厚度越大,锚链受到的拉力就越大。而冰速变化对锚链的受力影响不大。这也与Wright[31]与Zhou 等[32]的研究成果相符,即参照Kulluk 的经验,冰速与冰载荷大小之间并不存在相关性;冰速较低时,锚链拉力的最大值受冰速的影响很明显,而拉力的平均值与之关系不大。

图21 平整冰工况下5号锚链的拉力Fig.21 Tension of No.5 mooring line under level ice conditions
碎冰不同参数的作用效果如图22~24 所示。图22 中冰块的平均面积作为变量,在冰厚和密集度相同的条件下,平均面积越大,锚链受到的拉力就越大。从图中可以看出,在平均面积为100 m2的碎冰工况下锚链受到的拉力远大于在平均面积为20 m2的碎冰工况下的受力。图23 中碎冰场的密集度作为变量,在冰厚和冰块平均面积相同的条件下,密集度越大,锚链受到的拉力就越大。从图中可以看出不同密集度下锚链拉力的差异非常明显。碎冰场的密集度越来越大,冰块可运动的空间就越小。冰块会在结构附近大规模堆积,会引发冰载荷的增大。图24 中海冰厚度作为变量,在碎冰区海冰密集度和冰块平均面积相同的条件下,海冰越厚,锚链受到的拉力就越大。因为冰块的质量会随着冰厚的增大而线性增大,质量会影响动能进而影响在冰与结构物之间的作用力[33]。从图中可以看出,本文选取的三组不同厚度海冰的作用效果差别不大但符合规律。

图22 不同平均面积碎冰下的5号锚链拉力Fig.22 No.5 mooring line tension under different mean areas of ice floes
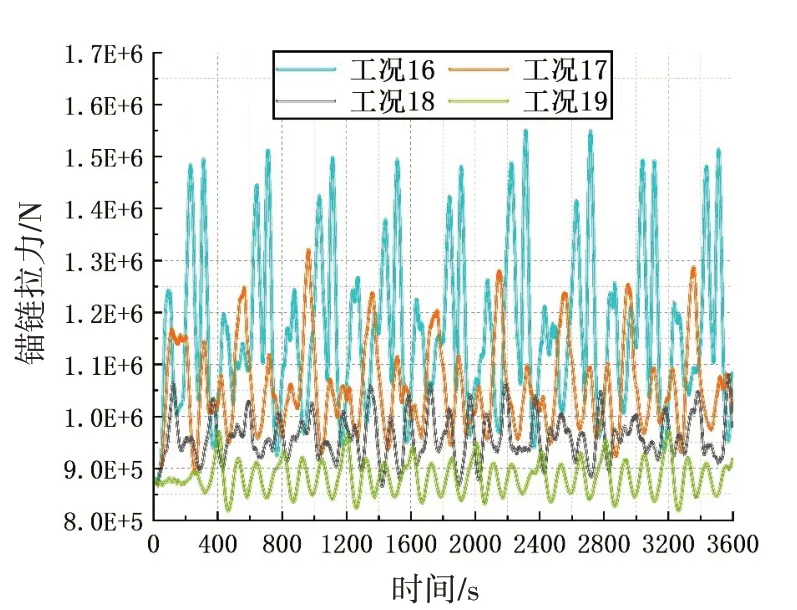
图23 不同碎冰密集度下的5号锚链拉力Fig.23 No.5 mooring line tension under different concentrations of ice floes

图24 不同碎冰厚度下的5号锚链拉力Fig.24 No.5 mooring line tension under different thicknesses of ice floes
3.3 波浪载荷和冰载荷下的动态响应对比
本文的重点是为了验证半潜式海洋平台在结冰和开放水域两种不同的环境下是否都能进行正常的海上作业,需要对比在波浪载荷和冰载荷作用下的锚链受力情况以及平台的运动情况,分析时采用了时域比较法和统计学两种方法。
通过折线图来观察时域分析下锚链的张力。时域分析的优点在于可以直观了解到一定时间范围内力的变化情况(本文选用的是3600 s内的数据),样本值更多,作对比分析时就更具有说服力。本文对比了波浪载荷作用下的工况1、工况4,平整冰作用下的工况6、工况12 以及碎冰作用下的工况15、工况18。具体情况如图25所示。从图中可以看出,平整冰作用下锚链受到的拉力远大于波浪载荷下受到的拉力。碎冰工况下的整体趋势会略高于波浪下的工况,从中体现出碎冰作用下锚链受力的平均水平略大于波浪作用下的受力。

图25 波浪、平整冰、碎冰工况下的5号锚链拉力对比Fig.25 Tension contrast diagram of No.5 mooring line under the wave,level ice,and ice floe conditions
图26为利用统计学进行分析的波浪、平整冰和碎冰工况下锚链最大拉力的对比图。三类不同的工况在柱状图中分别用三种不同的颜色加以区分。从图中可以看出,波浪和碎冰对锚链产生的最大拉力在同一水平线上,都远远小于平整冰的影响。

图26 波浪、平整冰、碎冰工况下的5号锚链最大拉力Fig.26 Maximum tension of No.5 mooring line under the wave,level ice,and ice floe conditions
沿180°方向的载荷对平台的纵荡和纵摇影响最大,本文着重对比不同载荷的纵荡运动和纵摇运动。图27~30 展示了同一入射方向上波浪、平整冰、碎冰三种不同环境下平台的运动情况。其中,图27为时域下纵荡运动的对比情况,从图中可以很明显地看出,在平整冰作用下平台的纵荡运动远大于波浪载荷下的运动,甚至相差数倍;碎冰作用下的纵荡运动介于平整冰与波浪之间。规范对深水区作业的半潜式平台的运动响应有具体要求。在正常的工况下,平台的纵荡运动一般不超过工作海域水深的10%,在恶劣环境的工况下,对平台运动响应的要求没那么严格,只需确保平台极限水平偏移量不超过水深的15%即可。本文计算的水深为330 m。图28 为统计学散点图,红线下方浅蓝色的点为符合规范的工况。从图中可知,波浪载荷作用下平台最大的纵荡运动可以控制在10%水深的范围内,而在平整冰的作用下,纵荡运动已经远远超过了水深的15%,甚至超过了水深的35%。对于碎冰来说,合适的海冰厚度、海冰密集度以及冰块平均面积会使得平台的运动能够满足现有规范的要求。在本文中,工况13、工况18、工况19以及工况20就是能保证正常海上作业的碎冰区。

图27 波浪、平整冰、碎冰工况下的平台纵荡对比Fig.27 Comparison of platform surges under the wave,level ice,and ice floe conditions

图28 波浪、平整冰、碎冰工况下的平台最大纵荡Fig.28 Maximum surge of the platform under the wave,level ice,and ice floe conditions
图29为时域下纵摇运动的对比情况。与纵荡的结论类似,在平整冰作用下平台的纵摇运动要大于波浪载荷下的运动,碎冰作用下的纵摇运动介于二者之间。对于深水区的半潜式平台,摇角一般要控制在10°以内。如图30所示,波浪载荷下平台的纵摇运动满足此规定,但是平整冰作用下的纵摇角度在某些工况下达到了25°,严重影响正常的工程作业。文中选择的碎冰工况,其作用下的纵摇运动均符合当前规范的要求。

图29 波浪、平整冰、碎冰工况下的平台纵摇对比Fig.29 Comparison platform pitches under the wave,level ice,and ice floe conditions

图30 波浪、平整冰、碎冰工况下的平台最大纵摇Fig.30 Maximum pitch of the platform under the wave,level ice,and ice floe conditions
4 结 论
本文研究了无冰与有冰两种不同情况下半潜式海洋平台在极地海上作业时的动态响应。无冰期时,平台在波浪载荷作用下进行生产作业,在波浪方向相同的情况下,有义波高和谱峰周期是需要考虑的影响因素。结冰期时,平台会受到海冰的撞击。对于平整冰来说,冰厚相较于冰速对平台运动和锚链张力的影响更大。为了保证海洋平台能够进行正常的海上作业,海冰管理是必不可少的一环,因此对碎冰的研究非常重要。研究碎冰时选择的变量包括海冰厚度、碎冰区的密集度以及冰块的平均面积。通过分析波浪载荷和冰载荷作用下平台的运动和锚链的张力,可以得到以下结论:
(1)对碎冰来说,在冰厚和密集度相同的条件下,冰块平均面积越大,锚链的张力就越大,平台的纵荡和纵摇也越明显;在冰厚和冰块平均面积相同的前提下,随着碎冰区密集度的增大,锚链张力和平台运动也会相应增大。在碎冰区的海冰密集度和冰块平均面积都相同的情况下,海冰越厚,对平台和锚泊系统产生的作用效果就更剧烈。归根结底,这三个变量都与海冰的质量息息相关。海冰的质量会影响海冰的动量,海冰动量的增大会最大程度影响海冰与结构物之间的作用力。
(2)结合时域分析和统计学两种方法可知,锚链在平整冰作用下的张力远大于波浪载荷和碎冰下的张力。在平整冰的作用下平台的纵荡运动和纵摇运动也远大于波浪载荷和碎冰下平台的运动。在平整冰的工况下进行海上作业危险性极大,而海冰管理后产生的碎冰区也无法完全保证平台的安全。碎冰对平台纵荡运动的影响大于纵摇运动,因为在有些碎冰工况下,平台的纵摇运动满足规范的要求,而纵荡运动则超过规范规定的最大偏移。故在极地进行油气开采时除了海冰管理的要求外,还要尽可能地减小冰载荷对平台纵荡运动的影响。
