低密集度浮碎冰数值生成方法研究

2022-02-10张忠宇谷家扬王志东陶延武渠基顺李文娟

船舶力学 2022年1期

张忠宇，谷家扬，王志东，陶延武，渠基顺，李文娟

（江苏科技大学 a.海洋装备研究院；b.船舶与海洋工程学院，江苏镇江 212003）

0 引言

全球气候变暖导致极地海区海冰发生融化，且波浪等因素推动海冰向外漂移，使得冰区密集度沿着纬度逐步递减，至冰缘区可降低至20%左右。低密集度冰况使得极地商业航行及油气资源开发作业变为可行。冰缘区海冰主要以浮碎冰的形式存在[1]，其中直径小于2 m的海冰称为碎冰，大于2 m的海冰称为浮冰。浮碎冰的形成机理较为复杂，浮冰的演变是动力学和热力学的共同作用。首先夏季温度场会使冰的内力变小，冰排发生破裂形成大尺度浮冰，浮冰在温度场的作用下会继续发生融化。Perovich 等[2]通过一系列直升机航拍照片研究了夏季过程中浮碎冰密集度演变及浮碎冰的融化特性。Steele 等[3-4]指出大直径浮冰的融化速率明显大于直径小于30 m 的浮冰。因此，对于冰缘区尤其是低密集度冰况的海域，海冰的形式主要以小尺度浮碎冰为主。若在此海域航行作业，浮碎冰区的船舶阻力性能也是极地船舶设计的重要考量因素之一。

为了研究浮碎冰区的极地船舶阻力性能，首先需确定相关海域的海冰大小及分布。直接观测法是目前最主要的技术手段，通过航拍得到目标海域的浮碎冰图像，对图像进行处理即可模化海域的浮碎冰分布。为了便于统计分析规律，Rothrock和Thorndike[5]提出了浮碎冰等效直径分布的概念并讨论了衡量浮碎冰直径分布的方法。之后，一系列的研究工作[6-9]采用卫星或航拍等手段研究了浮碎冰等效直径的分布，并发现浮碎冰的数量随其等效直径呈指数分布，幂指数为-β。在鄂霍次克海南部，Toyota等[10-11]通过航拍和船载摄像系统研究了鄂霍次克海南部海域的浮碎冰分布，当浮冰直径在25 m到50 m 之间时，β的取值减小到1.15 左右。Toyata 等认为这种现象是由于浮碎冰的膨胀导致的。而Steer和Lu等[12-13]通过研究航拍照片发现，浮碎冰数量分布在几十米直径范围内会发生急剧的变化，但对于小尺度浮碎冰区域，β的取值在1.9左右，这与Toyota等之前的结论相差较大。为了分析原因以掌握浮碎冰的分布，Toyota 等[14]又通过航拍研究了Weddell海域浮碎冰的分布情况，浮碎冰的直径在1 m到100 m 之间。冬季由于浮碎冰受膨胀因素的影响较小，所以β的取值较小。对于鄂霍次克海，β∈[1.0,3.0]。但由于极地恶劣的环境，难以到达目标海域进行数据采集，且航拍的成本较高，相关资料相对较少。

可见，数据的缺乏导致浮碎冰分布的理论还处在逐步完善阶段。另外一种方法是基于浮碎冰随机生成理论，对目标海域进行数值划分得到浮碎冰分布。朱红日等[15]基于二维Voronoi 图方法对碎冰域进行随机切割以生成碎冰区中冰块的几何形态，从而确定碎冰区的初始分布场。但这种方法生成的碎冰直径呈正态分布，与实际观测的规律不符。Yulmetov 等[16]开发了一套生成指数分布的碎冰程序，但其只是简要介绍了基本理论，并未详细阐述浮碎冰的生成过程。总之，低密集度碎冰无论从物理生成机理还是数值生成方法均处于起步阶段，相关资料较少。为了得到合理的浮碎冰场分布，本文在Yulmetov 等[16]工作的基础上，将Voronoi 图方法、概率理论等进行有机结合，形成给定密集度下浮碎冰的生成方法，为浮碎冰场的数值建模提供合理的输入。

1 低密集度浮碎冰随机生成理论

1.1 目标海域数值划分的Voronoi图方法

通过与实际航拍的浮碎冰场进行对比，浮碎冰的形状与Voronoi图类似。Voronoi图[17]是1908年由俄罗斯数学家Voronoi 提出，可对目标域完成几何随机划分。其在目标域生成一组随机点，按照最邻近原则划分平面，每个点与它的最近邻区域相关联，采用Delaunay 三角剖分法生成二维Voronoi图，将目标域分割为一组泰森多边形集合。可见，为了得到Voronoi图，首先需生成二维随机点，传统的做法是通过随机生成器生成伪随机数，这些随机数满足泊松概率分布。但对于二维随机数，在生成的过程中，新生成的随机点与前面的点是独立的，两个随机点间距离可能极大或极小，生成尺度极大或极小的浮碎冰，不符合实际海况。为了避免这种情况发生，本文采用Simple Sequential Inhibition(SSI)方法[18]生成二维随机点，该方法的思想是首先生成一系列随机点，给定随机点之间的最大距离为s，若随机点间的距离r与最大距离s的比值小于某一数值δ，则将该随机点剔除。其中，最大距离的定义为

式中，A为碎冰域的面积，N为随机点的数量。为了定性分析最大距离的影响，定义正则参数δ=r/s，该参数的影响将在后文中进行讨论。

1.2 量化碎冰尺寸分布概率函数

在采用Voronoi图对碎冰域进行划分后，浮碎冰的数量随其等效直径D分布函数呈正态分布。而依据航拍的试验数据可知，浮碎冰的数量随其等效直径D呈指数分布，如下式所示：

式中，NI为浮碎冰的数量，α和β为常数。

由式（2）可知，其累积分布函数F(D)为

式中，Dmin为浮碎冰的最小直径。

由累计分布函数的性质可知：

式中，Dmax为浮碎冰的最大直径。

将式（4）代入式（3）可得碎冰场的概率密度分布函数f(D)为

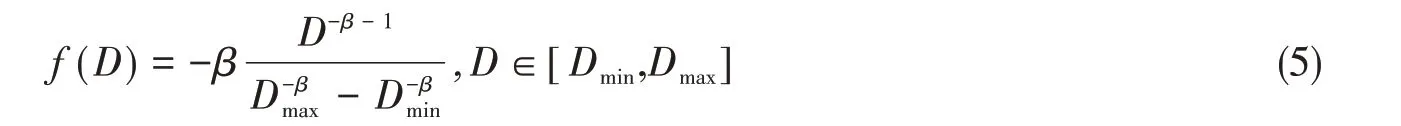
为了使得浮碎冰分布服从指数分布，需对Voronoi图中的泰森多边形进行量化处理。由泰森多边形的性质可知：

由随机变量商的性质，可得量化因子的概率密度等效函数为

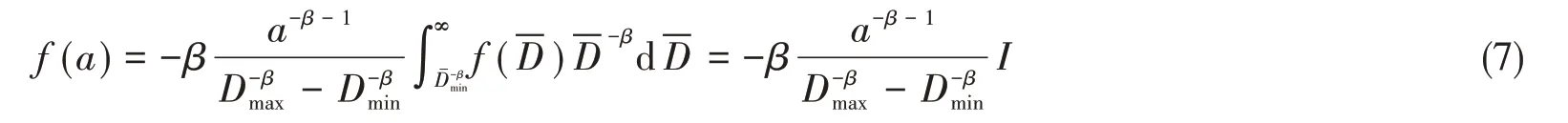
式中，I为关于的积分，对于给定的β和较大的浮碎冰数量N（随机点的数量），其积分为常数。但当浮碎冰数量较大时，影响数值的计算效率，对于其取值，本文将在后续进行讨论。

通过累积分布函数的性质对式（7）进行推导[16]可知：

式中，x为在[0,1]内的均匀分布随机数，本文通过Matlab的随机生成器获得。

通过式（8）得到量化因子，进而得到量化后的浮碎冰直径。通过给定的密集度，依次选取不同直径区间的浮碎冰，使其满足密集度的要求。

但量化浮碎冰尺寸后的浮碎冰场存在数值重叠，对于未受扰动的低密集度浮碎冰场，其不存在重叠现象，需对重叠区域进行数值消除。本文主要采用分离轴定理进行处理，遍历泰森多边形的每条边，将重叠最小的轴作为分离轴，让重叠的泰森多边形沿分离轴向相反方向分开即可，如图1所示，具体过程详见文献[19]，本文不再详细赘述。

图1 浮碎冰重叠区域分离示意图Fig.1 Separation diagram of overlapped broken ices

2 数值结果分析与讨论

本章在低密集度浮碎冰随机生成理论的基础上，开展浮碎冰场的数值模拟，在验证方法有效性的同时，开展相关变量对浮碎冰分布特性的影响研究，得到低密集度下浮碎冰合理的空间分布。为了定性分析，数值模拟过程中目标海域均取为100 m×100 m，最大海冰直径为10 m、最小海冰直径为1 m。

2.1 随机点数N的影响研究

从低密集度浮碎冰随机生成理论可知，随机点数N主要影响Voronoi图生成的泰森多边形数量及量化过程中的式中的积分I。为了定性分析随机点数的影响，分别取N=3 000、4 000、5 000、10 000、20 000，开展密集度为0.3的浮碎冰场数值模拟，β取为2.5，正则参数δ取为0.1。

图2 为不同随机点数下等效直径的随机概率函数。从图中可以看到，由于数值模拟的目标海域面积恒定，随机点数的增加显然会导致生成的泰森多边形的尺寸较小。随机点数为20 000 时，等效直径的最大概率出现在0.78 m左右。随着随机点数减少，等效直径的概率密度峰值右移，概率密度曲线也会随之变“扁平”。对于目标海域浮碎冰场的数值模化，传统的处理方法是将Voronoi 图按密集度进行等比例分布，以达到给定密集度的目的。但通过图2可知，这种处理方法获得的浮碎冰直径基本上呈正态分布，与实验测量拟合的结果不一致。

图2 不同随机点数下等效直径的随机概率函数Fig.2 Random probability function of equivalent diameter under different numbers of random points

图3 为量化后不同随机点下浮碎冰的数值分布，其中红色实线为通过公式得到的浮碎冰直径的理论概率密度函数，蓝色直方图表征数值模拟的浮碎冰概率密度函数。从图中可以看到，不同随机点下数值结果均与理论值吻合相对良好，从而验证了本文方法的合理性。虽然量化前浮碎冰直径的随机概率函数不同，但量化后随机点数对数值结果基本没有影响。显然，对量化过程中式中的积分I，假设其为常数也是成立的，随机点数对其影响较小。表1 给出了各随机点数下不同直径区间内浮碎冰的数量，五种随机点数下生成的浮碎冰总数分别为697 块、691 块、701 块、696 块和691 块。从表中可以看出，在大于4 m 的直径区间生成的浮碎冰数量均相同，仅在较小的直径区间内浮碎冰的数量略有差异。以随机点数3 000下浮碎冰的概率密度为参照，表1还给出了各随机点下不同直径区间内浮碎冰概率密度误差。随着随机点数的增加，概率密度误差整体仍较小。可见，基于本文数值方法生成的浮碎冰场随着随机点数增加是收敛的。为了提高计算效率，本文在后续数值模拟过程中随机点数均取为3 000。

表1 不同随机点数下浮碎冰数量及概率密度误差Tab.1 Quantityandprobabilitydensityerrorsofbrokenicesunderdifferentnumbersofrandompoints

图3 量化后不同随机点数下浮碎冰数值分布Fig.3 Numerical distribution of quantified broken ices under different numbers of random points

2.2 正则参数δ的影响研究

为了定性分析正则参数δ的影响，分别取δ=0、0.05、0.1、0.2，开展密集度为0.3 的浮碎冰场分布数值模拟，β取为2.5。图4为不同正则参数δ下浮碎冰数值分布，横坐标为浮碎冰的等效直径，纵坐标为浮碎冰的数量，曲线上的标记点表征数值模拟中小于该直径区间的浮碎冰数量。由于随机点在生成的过程中是随机的，因而本文对每个正则参数开展了5 次重复性数值试验。从图中可以看到，当δ=0时二维点的生成是SSI方法的一种特例，即在初始二维点生成时，通过随机生成器生成伪随机数，新生成的随机点与前面的点是独立的，两个随机点间距离可能为极大或极小，不存在筛选过程。由于随机点的生成是完全随机的，导致重复生成的浮碎冰数量出现一定的离散度。从图4（a）的数值结果中可以看到，5 次数值结果的离散度相对较大，不利于后续对极地船舶冰阻力特性的定性研究。随着正则参数的增加（图4（b）），5次数值结果的离散度相对减小。当δ=0.1时，数值结果的离散度最小，各直径区间的浮碎冰数量基本相当。这是因为δ表征的是SSI 生成方法中随机点间的距离与最大距离之间的比值，通过控制δ的取值，删掉一些不符合要求的随机点，从而一定程度上降低了碎冰生成的随机性，进而间接控制生成浮碎冰的大小。但当δ=0.2 时，数值结果的离散度尤其是小直径区间的离散度反而进一步增大。显然δ的增加，会删掉一些处于小直径区间的随机点，使得生成浮碎冰的离散度增大。朱红日等[15]研究发现，当δ逐渐继续增加并趋于1时，所有随机点之间的距离趋近于相等。因而，此时生成的浮碎冰具有相同的几何形态，生成的浮碎冰直径难以满足指数分布。综合以上分析，本文在数值模拟过程中正则参数δ均取为0.1。

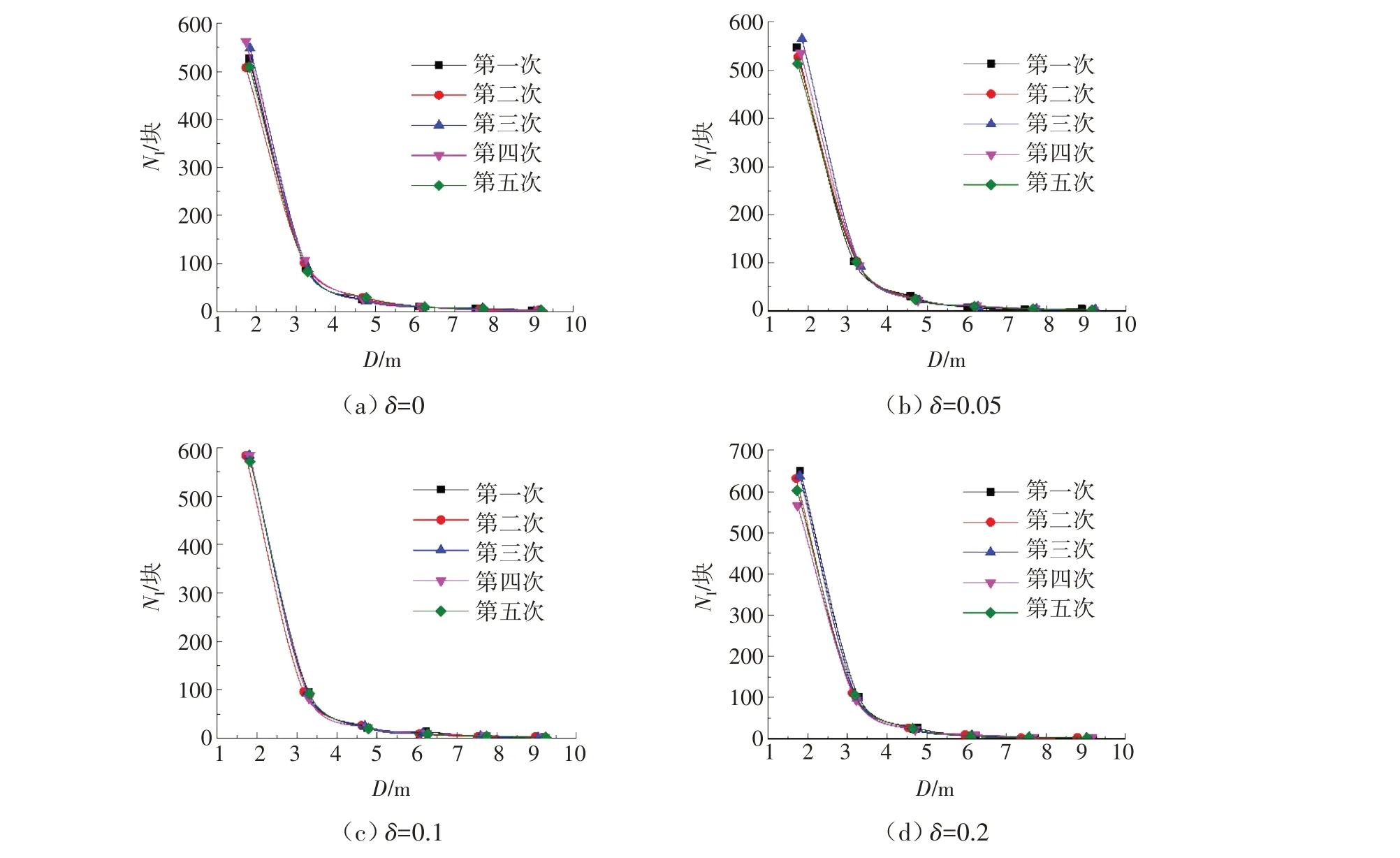
图4 不同正则参数下浮碎冰数值分布Fig.4 Numerical distribution of broken ices under different regular parameters

图5 给出了五次重复性数值模拟下浮碎冰的空间分布（δ=0.1）。从图中可以看到，虽然五次重复性数值模拟过程中各直径区间的浮碎冰数量基本相当，但在理论推导及数值计算过程中，未有变量控制浮碎冰的空间分布，因而五次重复性数值试验中最大海冰的空间位置各不相同。这种空间位置的不确定性对极地船舶冰阻力性能的影响规律，将是未来研究的一个重点。

图5 δ=0.1下浮碎冰的空间分布Fig.5 Spatial distribution of broken ices at δ=0.1

2.3 参数β的影响研究

由公式可知，参数β是影响浮碎冰分布概率密度函数的一个重要参数。为了定性分析参数β的影响，分别取β=2.5、3.0、3.5、4.0，开展密集度为0.3的浮碎冰场数值模拟。

图6为不同参数β下碎冰的数值分布。从图中可以看到，参数β是影响浮碎冰分布的一个重要因素。随着参数β的增加，较大直径区间的浮碎冰数量迅速下降，这从图7 中也可以看出。为了保证目标海域的密集度不变，较小直径区间的浮碎冰数量迅速增加。图7（d）中较小直径区间的浮碎冰数量达到776块，目标海域被小尺度碎冰覆盖。可见，为了较为合理地数值模化目标海域，参数β的取值至关重要。从相关文献中可知，通过对航拍得到的实验数据进行拟合发现：不同海域参数β的取值不一样，低密集度区域参数β的取值通常在2.5左右。