武器弹药密集度试验分组的蒙特卡洛模拟研究
2020-07-06邹陈来王雨时王光宇张志彪
邹陈来,王雨时,王光宇,闻 泉,张志彪
(南京理工大学 机械工程学院,江苏 南京 210094)
武器弹药密集度是评估武器和弹药散布特性的一项指标,是武器和弹药射击精度的重要组成部分。能否精确分析武器和弹药系统的密集度特性,关系到武器和弹药设计指标的制定以及武器和弹药的靶场验收标准的制定,对提升武器系统战斗效能起着非常关键的作用[1]。对于常规兵器密集度试验,原有的试验资料、现行的国家军用标准和兵工行业标准均有规定,且要求密集度试验须分组、分不同天进行,高、低、常温条件须单独进行试验[2-6],所需用弹量多,投入成本高。
在20世纪70年代,华东工程学院公算教研室提出了武器弹药密集度试验不分组的新做法[7]。1979年编写的《火炮试验法》中,单纯密集度由原来的三天三组改为一天一组,而引起了争论[8]。就武器和弹药密集度试验是否应该分组的问题,在20世纪80年代我国弹药界和弹道界进行了深入讨论[9-25]。文献[9]通过列举试验数据,论述了分组试验各组方差相等是不成立的,不分组理论需要商讨,并引用了巴尔坎等人的密集度理论,即密集度本身是极不稳定的,组与组之间的密集度存在20%左右的变化,说明密集度试验有必要分组进行。文献[18]指出大量射击试验数据中各组试验方差存在差异,不能引出各组方差不相等的结论,并通过理论计算提出:不分组试验与分组试验相比,可以得到较高的估计精度,并且可以节省人力、物力。文献[10]通过Cochran统计量和最大F比统计量,对391批密集度试验的结果数据进行了假设检验,拒绝了分组试验各组理论方差相等的假设。
针对武器弹药密集度试验不分组试验法和分组试验法的优劣性及可行性问题的讨论,主要有2种截然相反的观点:①主张分组,方差反应了多种因素的影响,不只是武器弹药本身,还与被试品以外的条件密切相关,不同的试验条件可以得到不同的密集度试验结果[9-16];②不主张分组,因为不分组试验时的方差估计小于分组试验时的方差估计,不分组试验时方差估计精度更高[17-18]。文献[19]从经济性和估计精度两方面考虑,更倾向于不分组试验,但同时不否认立靶密集度试验分组的做法。
除以上2种观点外,文献[21-24]主张根据试验目的、试验条件以及试验对象的不同来确定是否需要分组试验。文献[8]主张现行的火炮、弹药密集度试验方法没有修改或统一的必要,单纯的密集度试验,火炮仍可采用不分组射击,弹药则可保持原来的分组射击规定,并提出中间误差的二次散布随用弹量的增加而减小,即用弹量越大,二次散布越小,而测得的中间误差精度越高(组与组之间的跳动也将越小);当用弹量趋向于+∞时,中间误差二次散布为0,即所求中间误差为理论值。文献[25]则认为密集度试验应追求不分组试验,但为了保证试验结果为同一“母体”,应分组试验。
关于武器弹药密集度试验,分组与不分组主张的差异在于进行分组试验时各组试验所得结果的方差是否相等[20]。文献[9-25]主要通过文字和列举试验数据的方式进行论述,其中少部分文献根据数理统计理论,将密集度的估计值作为与试验分组数m和每组发数n相关的χ2函数进行理论分析。随着计算机技术的发展,计算工具越来越发达,使得通过计算机进行大量数据的辅助分析成为可能。本文针对武器弹药密集度试验是否有必要分组进行的问题,借助计算机,应用蒙特卡洛方法,假设某弹药具有特定的密集度特性,并假设分组试验时各组试验结果的方差相等,且等于总体方差,对密集度试验的分组试验法和不分组试验法进行仿真对比研究。
除了上述武器弹药密集度试验之外,引信空炸作用时间(距离)精度试验、引信自毁时间精度试验、爆炸元件作用时间精度试验、爆炸元件威力试验等,也都属于一次性的破坏试验,目前均采用不分组试验法[26-27]或分组试验,但各组结果单独考核[28],未见有采用分组法。
1 密集度试验与蒙特卡洛法模拟方法简介
1.1 密集度试验简介
射击密集度是指在相同射击条件下,弹丸的弹着点相对平均弹着点的密集程度[29],是通过对较少数量样本参数的估计来评估总体分布参数的一种方法。射击的密集度可以根据射弹的弹着点位置按下式计算[30]:
(1)
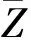
(2)
密集度试验是考核武器弹药射击散布的方法,式(1)计算所得为弹着点位置的中间误差,该散布范围包含了50%发数的弹着点。
在20世纪70年代提出的密集度试验新方法为不分组射击,按式(1)进行密集度估算。原有的试验方法及现行的试验方法为分组射击,按式(3)进行密集度估算:
(3)

(4)
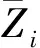
(5)
由文献[9]可知,分组射击时,样本密集度的估计存在2种算法,方法一为按式(3)计算,方法二为按式(6)计算:
(6)
现行国家军用标准及兵工行业标准对常规兵器密集度试验均有规定。其中文献[4]对反装甲弹的密集度试验作了要求,要求试验用弹样本量须按高温1~2组、常温3组、低温1~2组的组数进行,口径大于57 mm时,每组发数为7发,否则每组发数为10~20发,且要求一组射弹射击时间不大于30 min,一组射弹的各发时间间隔应尽量一致,各组之间的时间间隔应大于4 h。文献[5]则对火炮的密集度试验进行了规定,要求立靶密集度试验和地面密集度试验分组射击。对于同一组弹,发与发之间射击间隔为1~3 min,一组弹射击时间不应大于30 min。同一种药温的弹,一般射击3组,组间射击间隔应大于4 h。每组弹的发数按口径分,小口径每组10发,中口径每组7发,大口径每组5发。文献[6]对炮弹地面密集度试验法进行了规定,对炮弹进行工厂鉴定和外贸设计定型试验,每个试验组用弹量有如下规定:
①弹径在57 mm(含57 mm)以下每组试验10(或15)发(一般为3个试验组);
②弹径在60~100 mm(不含100 mm)每组试验10(或7)发(一般为3个试验组);
③弹径在100~160 mm(不含160 mm)每组试验7发(一般为3个试验组);
④弹径在160 mm以上每组试验5发(一般为3个试验组)。
按要求进行高、低温地面密集度试验时,试验用弹量参照常温试验用弹量。
火箭弹产品研制试验、工厂鉴定和外贸设计定型试验组用弹量则参照文献[3]的规定。即:
地面密集度试验每组弹数根据实际情况确定。对多管火箭炮连放射击通常每组发数取“一次连放的弹数”;对单管火箭炮或多管火箭炮单放射击,大口径火箭弹每组5~7发,中小口径每组7~12发。一般高、低、常温各3组。一般一天内高、低、常温各射击一组,三天射击完毕。一组射击时间应在30 min之内,最长不应超过45 min。
以上3个标准所规定的密集度估计均按式(3)和式(4)进行。按以上规定进行密集度试验,均要求高、低、常温各射击3组,所需试验弹数较多,耗时较长。为减少试验用弹量,文献[31]根据某榴弹和某爆炸成型弹丸的常温、高温、低温密集度试验结果,提出温度对密集度的影响较小,建议以常温考核为主,高温、低温考核为辅的方法进行立靶密集度考核。文献[32]通过数理统计理论建立方差检验模型,对密集度散布方差进行了检验分析,提出弹温对密集度散布没有影响,而分组试验可以消除偶然因素带来的不利影响,并建议轻武器榴弹密集度试验采用单一温度条件下射击多组的方法试验。
1.2 密集度试验的蒙特卡洛法模拟的实现
蒙特卡洛法是一种随机抽样方法,其通过数量足够大的模拟试验来逼近服从特定分布的实际总体,该方法的理论基础为概率论的大数定理和伯努利定理。只要进行足够大量的模拟计算,蒙特卡洛法的应用几乎没有限制[33]。
蒙特卡罗法模拟密集度试验需要产生弹着点位置坐标,弹着点位置坐标是试验中的随机变量,其产生服从选定的分布概率模型。在此假设其服从正态分布模型。
设共有试验样本K批,每批试验的总用弹数为N,分m组射击,每组射击n发。则K批样本的均值和方差为
(7)
(8)

通过估计量的精度来评估估计量的优劣,估计精度的指标包括估计均方差σB和估计相对误差EB:
(9)
(10)
对于分组试验,可根据同一批试验中估计值最大一组的密集度与估计值最小一组的密集度的比值γ,来评估组与组之间的密集度差异大小:
(11)
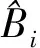
同一次模拟(包含K批样本)中比值最大值γmax为
γmax=max{γk}
(12)
式中:γk为第k批样本的比值。
则K批样本的均值和均方差为
(13)
(14)
2 蒙特卡洛法模拟
不妨假设某弹药的弹着点位置坐标服从N(0,202)的标准正态分布,则该弹药密集度真值B=13.49 m。国家军用标准对密集度试验用弹数的规定,包括5发一组、7发一组和10发一组的做法,组数一般要求3~6组。现假设产品单批试验样本总量N分别为5发、7发、10发、14发、15发、20发、21发、25发、28发、30发、35发、40发、42发、50发和60发,用蒙特卡洛随机抽样方法模拟不同分组方式的密集度试验,求取每个样本的统计量B的最大似然估计值作为观察值。模拟试验批数K分别为104,105,106。
表1所列为密集度试验分组试验法散布参数的2种估计方法的对比,其中方法一为按式(3)进行估计,方法二为按式(6)进行估计。
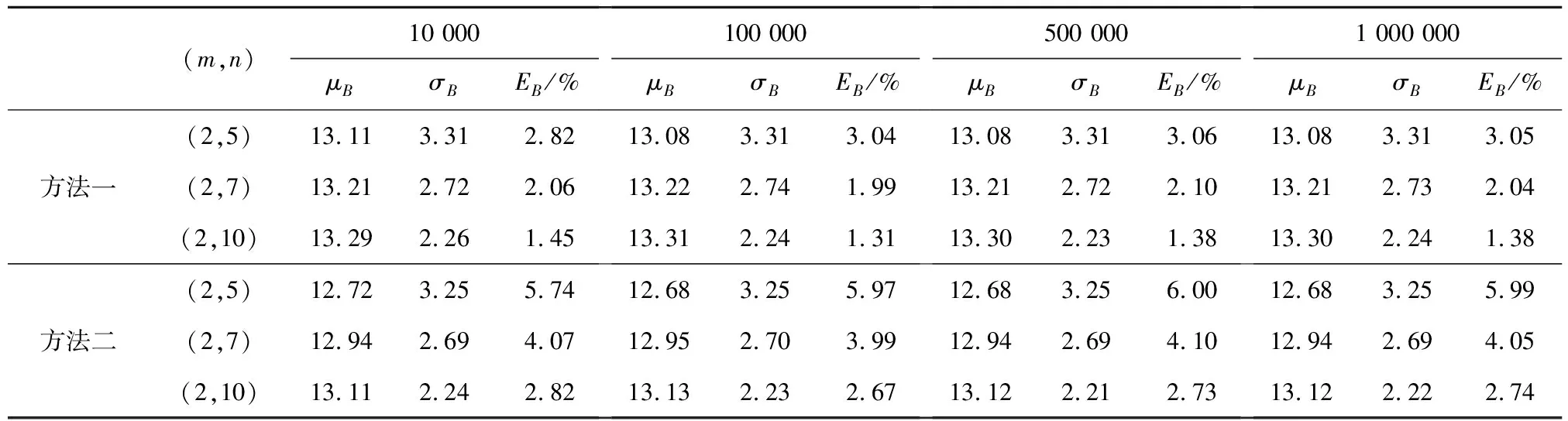
表1 N(0,202)标准正态分布密集度试验分组试验2种估计方法模拟结果对比
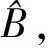
为评估式(3)和式(6)2种估计方法的差异,得到组间密集度比值不同时2种估算方法的相对偏差大小为
(15)
式中:μ1为按式(3)进行估算所得的密集度估计值,μ2为按式(6)进行估算所得的密集度估计值。
表3所列为试验样本总量N为10,14,15,21,25,28,30,35,40,42,50和60时,按不同分组方式进行抽样模拟,得到的组间密集度差异的估计参数γ、2种不同估计方法所得密集度估计值μ1和μ2以及两者之间的相对偏差大小Δ12。
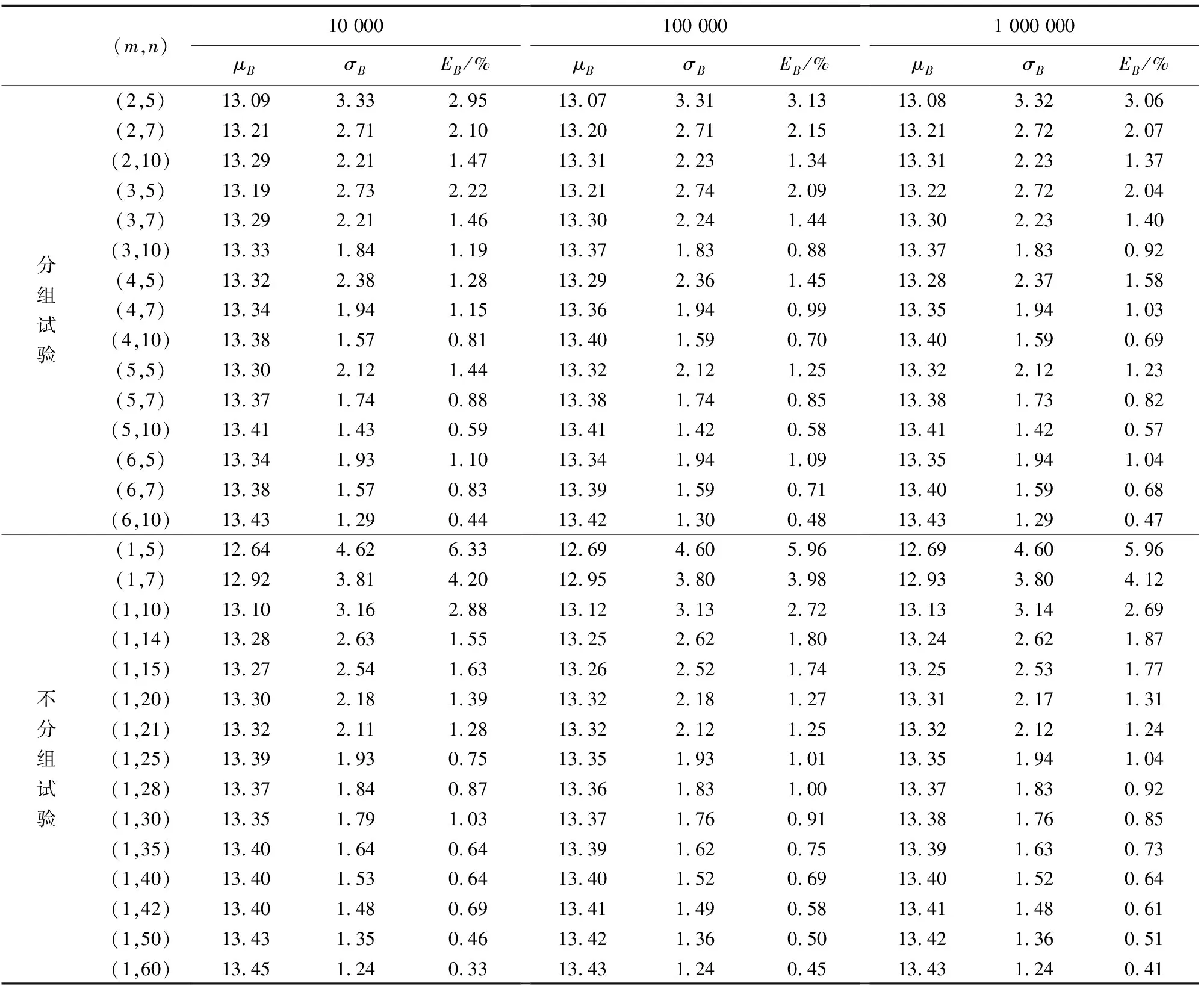
表2 N(0,202)标准正态分布密集度试验分组试验与不分组试验的模拟结果
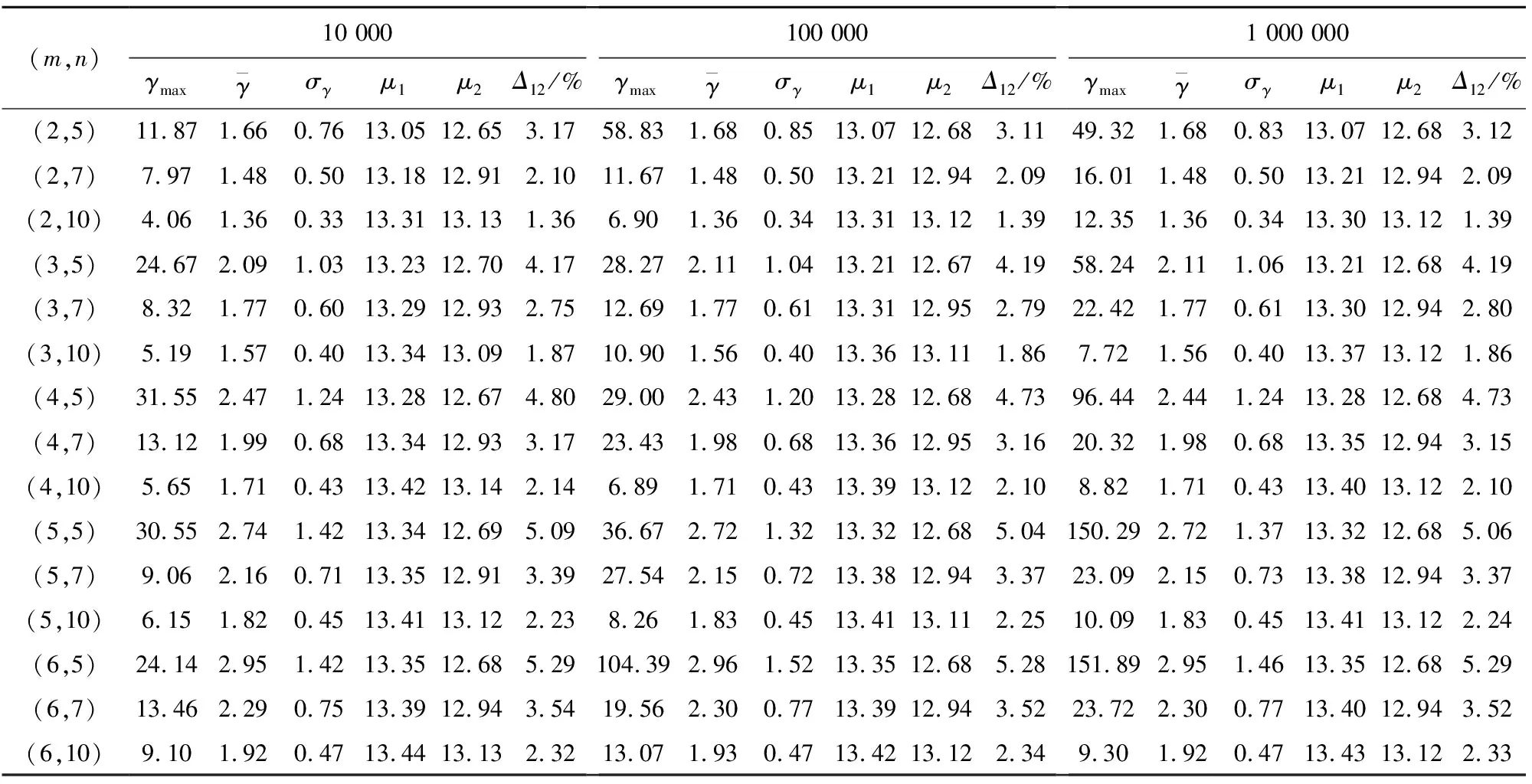
表3 N(0,202)标准正态分布密集度试验分组试验组间密集度最大比值γ以及2种密集度估算方法模拟结果对比
3 分析讨论
由表2分组密集度试验106批次模拟结果可知,每组试验射击5发,射击2组所得密集度估计相对误差为3.06%,射击3组所得密集度估计相对误差为2.04%。每组试验射击7发,射击2组所得密集度估计相对误差为2.07%,射击3组所得密集度估计相对误差为1.37%。每组试验射击10发,射击2组所得密集度估计相对误差为1.37%,射击3组所得密集度估计相对误差为0.92%。即每组射击5发时,射击3组及3组以上,即可得到较好的密集度估计精度;每组射击7~10发时,射击2组及2组以上,也可得到较好的密集度估计精度。
对表2模拟计算结果进行统计,得到不同试验样本总量,不同分组方式,按106批次进行模拟得到的计算结果,如表4所列,其中分组试验的密集度是按式(3)~式(5)的方法计算的。
结果表明,试验样本总量N一定时,加大分组数m,样本均方差增大,样本估计相对误差也增大,即估计的无偏性降低,估计精度也降低。与文献[18]中所述对于总用弹数一定时,分组数越大估计无偏性越差的结论是一致的,与文献[9]中引用的不分组理论也是一致的,即密集度估计精度随着分组数增多而降低。密集度试验不分组进行比分组进行可以得到更高的估计精度,但精度增加十分有限。
由表2中106批次模拟结果可知,估计相对误差随着样本量的增加而减小。试验组数m相同时,单组用弹量越大,密集度均方差越小,即密集度估计的散布越小,所得结论与文献[8]中关于中间误差二次散布随用弹量的增加而减小的结论是一致的。不分组试验,试验样本量为5发时,估计相对误差为5.96%;试验样本量为7发时,估计相对误差为4.12%;试验样本量为10发时,估计相对误差为2.69%;试验样本量为14发时,估计相对误差为1.87%;试验样本量为21发时,估计相对误差为1.24%;试验样本量为28发时,估计相对误差为0.92%。即不分组试验,单次试验射击14发或14发以上即可得到较好的密集度估计精度。
根据表3中106次模拟的结果,试验总发数15发,分3组试验,每组5发时,各组中间误差极大值与极小值之比最大为58.24,均值为2.11。试验总发数21发,分3组试验,每组7发时,各组密集度之间的最大比值的最大值为22.42,均值为1.77,按3倍均方差为误差区间,则组间密集度最大比的有效范围为1.00~3.60,文献[9]所列举试验数据组间密集度的比值基本在这个范围内,个别组比值超过3.60,但仍未超过模拟计算所得的最大值22.42。因此,单批试验组与组之间的密集度差异大,不能得出各组样本不属于同一母体的结论。与文献[18]关于大量射击试验数据中各组试验方差存在差异,不能引出各组方差不相等的结论的论述是一致的。
根据各组密集度之间的最大比值的106次模拟结果,试验总发数15发,分3组试验,每组5发时,各组密集度之间的最大比值的均值为2.11,则组间密集度的平均差异约为35.7%。试验总发数21发,分3组试验,每组7发时,各组密集度之间的最大比值的均值为1.77,则组间密集度的平均差异约为27.8%。试验总发数30发,分3组试验,每组10发时,各组密集度之间的最大比值的均值为1.56,则组间密集度的平均差异约为21.9%。即组间密集度存在一定的差异,其差异大小随单组试验发数的增加而减小,随试验组数的增加而增大。所得结果与文献[8]关于密集度组间跳动随用弹量增加而减小的结论以及文献[2]关于组间密集度存在20%左右差异的结论基本一致。
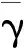
4 结束语
不考虑气象等因素,从纯数学角度,假设弹药具有特定的密集度特性,密集度试验分组进行会降低密集度的估计精度,密集度试验由分组进行改为不分组试验可以提高估计精度,但估计精度改善不明显。现行国家军用标准和兵工行业标准均要求密集度试验分组进行,可以计入气象等随机因素带来的影响。
对于引信空炸(自毁)作用时间(距离)精度、爆炸元件作用时间精度、爆炸元件威力等一次性破坏试验,从理论上讲,采用分组试验进行评估同样可以计入不确定随机因素的影响,从而提高估计精度。但这类试验分组进行成本往往较高,而带来的效果却并不十分明显,引信和火工品专业可能因此而一直采用不分组试验方法。
采用分组方法进行武器弹药密集度试验时,如果单组试验发数为5发,则应射击3组或3组以上。如果单组试验发数为7~10发,则应射击2组或2组以上。对于分组试验密集度估计,应使用各组密集度的几何平均值作为总体密集度的估计。
