非定常流场时程重构的深度学习方法

2024-03-22战庆亮白春锦吴智虎葛耀君

船舶力学 2024年3期

战庆亮，白春锦，吴智虎，葛耀君

（1.大连海事大学交通运输工程学院，辽宁大连 116026；2.同济大学桥梁结构抗风技术交通行业重点实验室，上海 200092）

0 引言

高分辨率的流场数据对于流体力学的研究至关重要，如船舶绕流分析[1-2]、海洋结构的绕流[3-5]及流固耦合问题研究等。然而，高分辨率流场的直接获取往往存在一些困难：在数值模拟领域，实现高分辨率的流场数据需要增加计算网格的密度，而这也伴随着求解效率的降低；在流体实验方面，流场中的某些位置可能无法布设传感器，而PIV 方法仍难以实现大范围的三维全场测量。针对这些问题，本文提出一种基于深度学习的高分辨率流场重构方法。

深度学习方法能够有效地分析复杂数据的内在规律，因而在处理流场的强非线性特性方面具有突出优势，为流体力学的研究提供了新的方法[6]。例如在基于数据建模的湍流模型研究中发挥了重要作用[7]，将数据与物理信息相结合可得到更高精度的湍流模型[8]，是一种重要的新的研究方法[9]。另一方面，深度学习方法在复杂流动的模态分解[10]、流固耦合分析[11]等方面得到了应用。同时，深度学习方法也可用作偏微分方程的求解新工具[12]，进一步实现流场与结构的耦合分析[13]。

深度学习方法也成为了流场重构问题的新的研究方法与热点[14-15]。例如Maulik 等[16]提出了单层前馈人工神经网络模型，可以将低分辨率且包含噪声的流场数据还原得到可靠的高分辨率流场；Fukami[17]提出了混合下采样跳过多尺度模型，同样实现了由低分辨率图像重建高分辨率的湍流流场数据，且该方法能较准确地保留湍流动能谱；Liu[18]提出的多时间路径卷积神经网络以速度场时间序列作为输入，融合了连续流体场的时空信息，可精确提取时间相关信息，成功用于湍流和各向异性通道流的超分辨率重构；Kim[19]借助循环一致生成对抗网络成功地克服了监督学习的数据配对要求，能够使用未配对的湍流数据进行训练，以实现湍流场的超分辨率重建。

前述深度学习技术专注于处理流场的实验数据或模拟数据快照，运用图像重构技术以完成数据处理。本文从时程数据的特征提取与表征方式出发进行流场重构，其中文献[20-22]对流场时程特征的提取方法开展了研究，为本文的重构模型提供了依据。本文通过建立非定常流动数据的低维表征模型，构造物理空间与编码空间的对应关系，并采用解码器生成新的时程数据，方法面向时程数据且具有较高的时间维度准确性，相比于传统基于快照的重构方法具有一定的优势。

1 非定常流动的低维表征模型

流体受到固体表面的干扰后，会形成复杂的流动分离等现象，导致流场中不同区域内的流动特征各不相同，这种非定常流动系统不仅具有高度复杂性还蕴含了丰富的流动特征。前期的研究结果表明，一维卷积的深度学习模型可以准确地捕捉到时程的流动信息，并以更低的维度表征这些特征。因此，对时程的流动信息进行准确的低维表征是流场高分辨率重构的关键。在此基础上，本文提出基于一维卷积流场时程自动编码（flow time history autoencoder,FTH-AE）的流动低维表征模型，将高维时序特征映射到低维抽象空间内，简化流动系统的复杂度。

图1所示模型结构包含五个主要部分，即输入层、卷积编码层、特征代码层、卷积解码层以及输出层。输入层接收流场不同位置处的时程数据x，经过编码过程以提取和压缩特征，进而获得低维特征向量λ；随后，特征代码经由卷积解码层进行还原，以产生与输入时程信号相等的输出x'。

图1 FTH-AE模型结构示意图Fig.1 Architecture of FTH-AE model

为保证时程特征重构的准确性，在构建FTH-AE 模型时，首先根据流场及其样本特征，选择合适的卷积编码器结构；其次，编码器与解码器需满足下式的变换，来保证特征代码λ可以准确表征输入x的特征：

式中，Fe表示卷积编码器，Fd代表卷积解码器，x为输入的流场时程数据，λ为流场时程的特征编码。由其结构可知，在FTH-AE 模型中输入数据与输出数据具有相同的属性，即两者时程的长度与采样间隔是相同的。本文的FTH-AE 模型采用无监督学习训练方法，模型输出时程后利用反向传播算法使其与输入时程尽可能相同，进而保证特征向量λ最大程度地保留了原有的数据信息。编码器中卷积层对输入数据的计算过程为

式中，T为输入数据的长度，l为卷积核的大小，K为当前层的卷积通道个数。在计算过程中，各通道采用了“共用权值参数w”的方法，在减少模型参数个数的同时共享了偏置矩阵b。基于流场时程的编码卷积计算原理如图2 所示，编码器通过卷积层从输入时程中逐层提取特征，且层数越深，特征的维度越低，抽象程度越高。在训练后，如果模型的输出数据与输入数据近似相等，则表明高维数据已成功映射到低维特征向量λ中。

图2 时程卷积的计算过程Fig.2 Time-convolutional calculation procedure

2 流场时程数据的生成方法

FTH-AE 模型建立了流场时程数据到其自身低维表征的映射关系，其中低维的特征向量λ、编码器与解码器共同实现了整个流场时程数据的低维表征。编码器建立了流场中不同位置处时程样本到低维度编码空间的映射，而解码器则将编码空间中的低维向量还原成物理空间对应位置处的时程信号。因此，求解出物理空间中任意点映射在编码空间的低维度特征向量，即可通过解码器生成该位置的流场时程样本，其原理如图3所示。

图3 时程的生成原理Fig.3 Generation method of FTH

如图3所示，已知物理空间中测点P1与测点P2的空间坐标位置及其时程样本，则可以通过编码器获得两个样本在编码空间中的编码P1'和P2'。对于物理空间中P1和P2附近的未知点r，即r点处的流场时程是未知的，此时可以根据P1、P2与r之间的几何关系，由P1'和P2'构造得到编码空间的r'，利用r'和解码器还原得到物理空间r处的时程样本，即平均向量组合法（average vector combination，AVC）。具体做法为：在r附近选择多对已知样本点，其坐标分量分别为pi与qi，采用两个物理空间中的已知样本点向量构造待求r向量，αipi+βiqi=r，从而得到编码空间中待求像的位置为

式中，n表示所进行平均的组数。

3 算例与分析

本文以低雷诺数下的圆柱绕流场为例，采用数值模拟方法获得流场数据，验证方法的准确性。计算域如图4 所示，雷诺数ReD=200。其中圆柱的直径为D，计算域的顺流向长为44D，横向长度为48D，上、下游长度均为22D。圆柱周围矩形区域内使用较密的非结构化三角形网格，距离圆柱较远的区域使用较稀疏的网格。左侧为来流入口边界，右侧是压力出口边界。

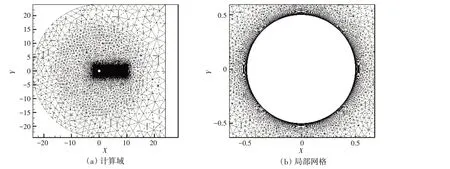
图4 整体及局部的网格划分Fig.4 Global and local meshes distribution

考虑到圆柱周围区域的流场特征更加丰富多样，在圆柱周围选取了6892 个测点，均匀分布在流场计算网格密集的矩形区域内，测点分布如图5所示。在流场计算的每个时间步结束时，输出各测点的流向速度与横向速度，得到两物理量的时程集合。

图5 测点位置示意图Fig.5 Location of sampling points

3.1 FTH-AE模型参数

FTH-AE 模型参数如表1 所示，编码器中三层卷积层的核数为128、64 与16，并使用尺寸为13 的大卷积核来获得更大的局部视野。经过卷积层逐层提取特征后输出样本的尺寸为1000×16。为了保留卷积权重与时程序列之间的对应关系，本文使用Flatten 层附加通道数为2的全连接层进行降维，最终将单个时程样本压缩为2 维空间中的一点。由于自编码器具有对称性，模型的解码部分各参数与编码部分相对应。

表1 自动编码特征降维模型参数Tab.1 FTH-AE model parameters

本文在训练时使用无监督学习模式，并在流场时程数据中随机选取50%的样本进行训练，另外的样本用作模型预测结果的验证集。模型优化器为Adam并设置学习率为默认参数，可通过自适应调整学习率加速模型收敛。模型训练时，Batch_size 大小设置为4，损失函数采用均方误差MSE，网络各层的激活函数均为ReLU。训练次数为200次的Loss 曲线如图6所示，随着迭代次数的增加，网络在训练50 次时Loss 曲线开始趋于稳定，训练100 次后Loss 曲线达到收敛值0.0005，训练结束后保存Loss值最优模型。

图6 FTH-AE模型的训练损失值Fig.6 Loss of FTH-AE with respect to epoches

3.2 模型表征的准确性验证

FTH-AE 模型在训练过程中不需要带有标签的样本，也不需要成对的样本，其训练目标是自身的解码误差最小。本文选用MSE 损失函数来衡量模型输入时程与输出时程的差异，损失值越小说明网络对输入数据特征提取越精准。为了直观展示模型的准确性，本文在整个流场区域随机选取了3条参数U、V的样本并比较原始曲线与模拟曲线的差异值。由图7 可知，原始数据与由低维编码还原得到的时程曲线差异很小，两条曲线几乎重合，说明模型可以准确地提取到流场中各个测点处数据的低维度特征，验证了降维模型的可行性。

图7 原始时程与FTH-AE模拟的时程Fig.7 Original samples and FTH-AE result

为验证整个流场中的模型解码精度，本文将各点位置处的输入时程与解码时程之间的相对误差进行无量纲化，记为Rerr（relative error），

式中，x为原始输入时程，x'为输出的解码时程，n为时程长度，max 与min 分别为时程的最大值与最小值。由于数据集中的时程曲线形态多样，相对误差Rerr更加合理地表示了各点误差与时程振幅之间的相对关系，直观地展示出解码时程对原始时程的拟合准确性。

将所得到的误差值赋予不同颜色并按照测点坐标绘制散点图，如图8 所示。其中绿色、蓝色、黄色、橘色和红色分别表示误差值为0～0.1、0.1～0.15、0.15～0.2、0.2～0.3 和0.3～0.5 的区域。由图可见，FTH-AE模型很好地对输入时程数据进行了低维表征，并准确地解码还原了输入时程。

图8 模型解码的误差分布图Fig.8 Error distribution of model reconstruction

3.3 模型预测的准确性验证

进一步对验证集中的测点物理坐标进行AVC 组合，获得这些点在编码空间中的坐标集。对坐标集中的编码坐标进行FTH-generate 解码预测，获得各点处的预测时程。同样随机选取了6 条预测时程，与CFD计算值进行了比较，如图9所示。

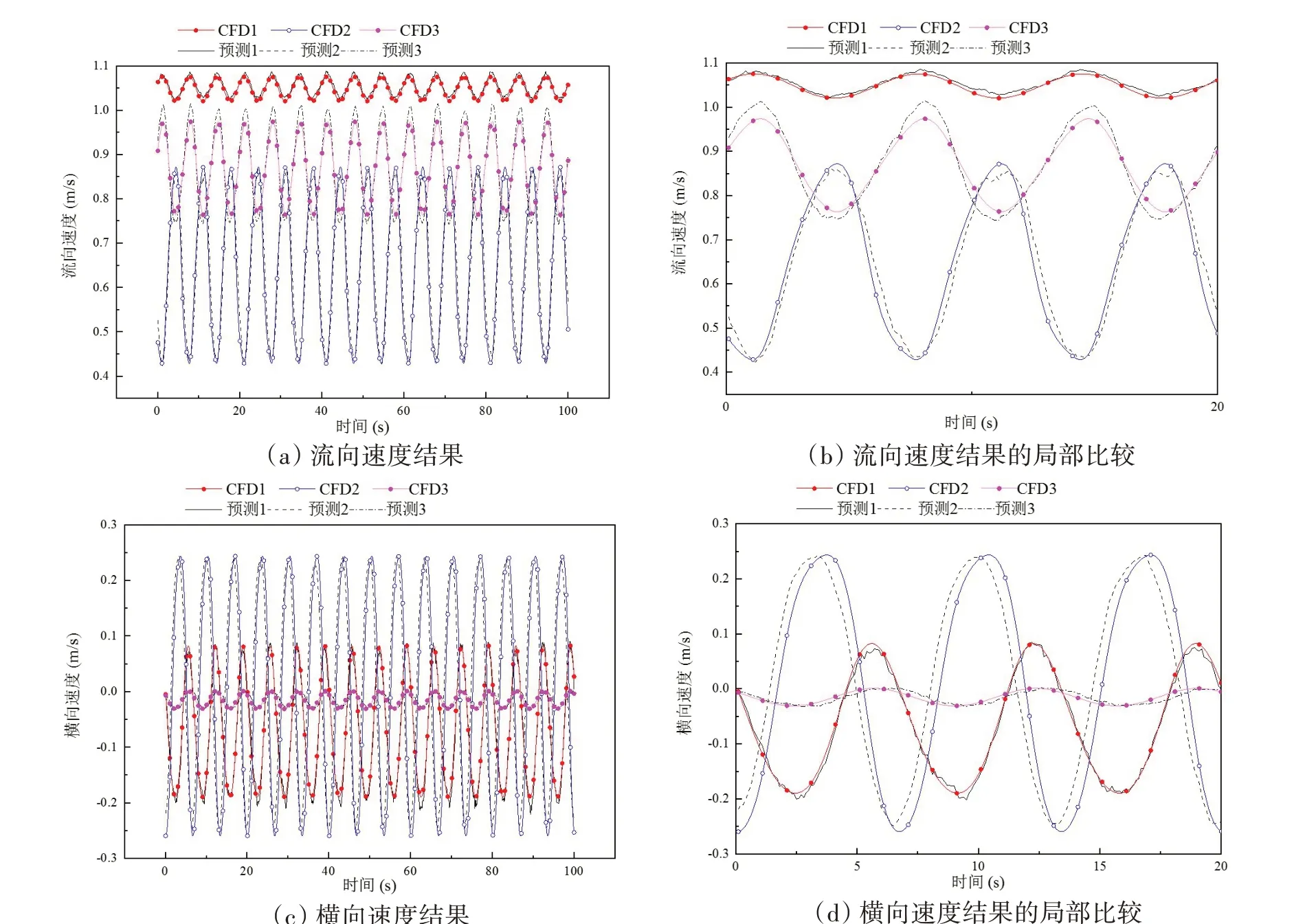
图9 模型的预测曲线Fig.9 Original samples and FTH-AE result

对比图9中的结果可发现，本文方法成功地对时程进行了预测，并求得各时程预测结果的相对误差，列于图10。比较图10 和图8 可知，预测时程的精度要低于还原时程精度，尤其在上游来流区以及圆柱壁面附近，相对误差较大。主要原因可分为两方面：一方面根据相对误差的定义，由于上游来流区域的流场波动较小，导致式（4）时程的最大值与最小值相差较小，因此相对误差较大；另一方面，圆柱表面附近流动梯度较大，在训练样本较稀疏的情况下流场的预测时程难以准确预测分离区内部流场的变化，导致相对误差较大。

图10 模型预测误差分布图Fig.10 Error distribution of model prediction

进一步地，对所有预测的流场时程数据取同一瞬时的值，就可以得到整个流场的瞬态结果，见图11。其中图11（a）和（d）分别为流向速度与横向速度的输入样本分布，图11（b）和（d）为FTH-AE 模型的预测结果，图11（c）和（f）为CFD 计算结果。由图中结果可以发现，本文方法成功地对稀疏的输入流场进行了较准确的重构，然而在部分位置预测结果出现了一定差异，计算方法仍需改进。