机翼弯曲模拟系统的建模与仿真研究

2024-03-21赵孟文樊泽明

机械科学与技术 2024年2期

赵孟文，樊泽明

（1.西安航空学院机械工程学院，西安，710077；2.西北工业大学自动化学院，西安，710072）

某型飞机在飞行过程中，机翼承受多种载荷发生变形，最大变形量可达3 m。机翼的弯曲变形，对装在机翼中用于飞行控制的钢索传动装置的操控产生极大影响。钢索传动装置的动态性能需要进行试验测试和验证[1]。设计了用于钢索传动装置地面半物理仿真试验的机翼弯曲模拟系统，系统由16 套电液伺服系统组成，模拟了机翼在飞行过程中变形而引起的钢索传动装置角度及位移的变化，建立了数学模型，分析了多因素耦合及多余力对系统的影响[2]，实现了对钢索传动装置的位移和角度变化量的精确控制。通过对试验现场工作状况和参数的采集、分析，以及设计了系统故障报警和处理，确保了试验系统安全。

1 试验系统的技术要求

1.1 主要指标

1）模拟变形时钢索传动装置上下移动速度：0～100 mm/min（连续可调）。

2）试验件倾角调节速度：0～20°/min。

3）测量精度：位移：优于0.5%FS（满量程误差不超过0.5%）；角度：分辨率优于0.2°。

4）控制精度：位置闭环：优于2%FS；角度闭环：误差不大于1°。

1.2 项目调试

由于目前仅能提供在飞机停放状态和飞行最大状态时的变形数据，目前研制的“机翼弯曲模拟实验系统”仅模拟停机和最大变形以及三分之二变形量状态[3]。主要调试项目如下：

1）同时驱动一侧钢索传动装置上的钢索传动装置至最低位置，以模拟停机状态下的钢索传动装置状态。

2）同时驱动一侧钢索传动装置上的钢索传动装置至最高位置，以模拟最大变形状态下的钢索传动装置状态。

3）在驱动钢索传动装置运动时，进行多套机构的同步检测与同步控制，以保证被试钢索的安全。

4）对试验设备、钢索传动装置的状态数据（位移、角度）等数据进行采集、监控。

2 机翼地面弯曲模拟系统及数学模型

飞机在飞行过程中，机翼受到不同的力而产生变形，安装在机翼中的钢索装置随机翼发生变动，但钢索装置的相对位置不变。钢索传动装置随机翼变形发生位置及角度变化的示意图如图1 所示。

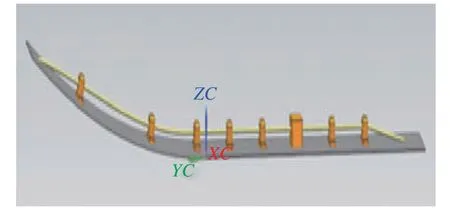
图1 钢索传动装置在机翼上安装位置及跟随机翼运动示意图Fig.1 Schematic diagram of the installation position of the cable drive on the wing and its movement following the wing

在该模拟系统中，沿机翼方向安装16 套台架，每个台架上都安装了控制钢索传动装置位移和角度的伺服控制系统。钢索传动装置的安装形式及坐标与试验的机体坐标相同。模拟系统结构图如图2所示。每个台架可分为台体、上下位移调节、绕左右轴旋转偏移角度调节、钢索传动装置4 个主要部分。台体部分结构图由图3 所示，由上板、下板、4 根支柱、前后倾斜导槽、双耳底座组成，主要承受整个台架和钢索传动装置的重力，且当钢索传动装置上升时与水平方向会有一个不断变化的夹角，此时双耳底座上的平台可以跟随钢索传动装置角度变化轨迹，从而保证丝杠推动上下移动机构沿着设计的轨迹运行。钢索传动装置位于4 根支柱的中间，沿机翼方向的钢索将穿过钢索传动装置的支撑机构中。上下位移调节部分由液压马达、减速装置、丝杠线性模组等部分组成，液压马达通过带有自锁功能的蜗轮蜗杆减速器驱动丝杠，丝杠通过一个带通轴的滑动底板带动钢索传动装置运动，并通过带有一条轨道槽的导向板限制其运行轨迹，上下位移调节部分主要是对钢索传动装置沿导槽上下、前后移动。绕左右轴旋转偏移角度调节部分主要是对钢索传动装置相对于水平面的角度值进行调节，由液压马达通过带有自锁功能的减速机构驱动钢索传动装置安置板上的轴来改变角度[4-6]。

图2 模拟系统结构示意图Fig.2 Schematic diagram of simulation system structure

图3 台体结构图Fig.3 The structurae of the platform

3 姿态控制建模分析

3.1 蜗轮蜗杆模型

系统采用蜗轮蜗杆减速器，并利用蜗轮蜗杆的自锁特征来提高系统的安全性。将蜗轮蜗杆看作为一个比例环节，控制模型为

3.2 丝杠模组建模

系统使用丝杠主要作用是把旋转运动转换成直线运动，推动钢索传动装置上下运行，在控制系统中滚珠丝杠可以看成是一个比例环节，其控制模型为Gg=10。

3.3 控制钢索姿态的阀控液压马达建模

系统中的姿态控制的动力机构，采用电液伺服阀控制液压马达，分别完成直线位移的驱动与控制及角度的控制[7]，其原理图如图4 所示。

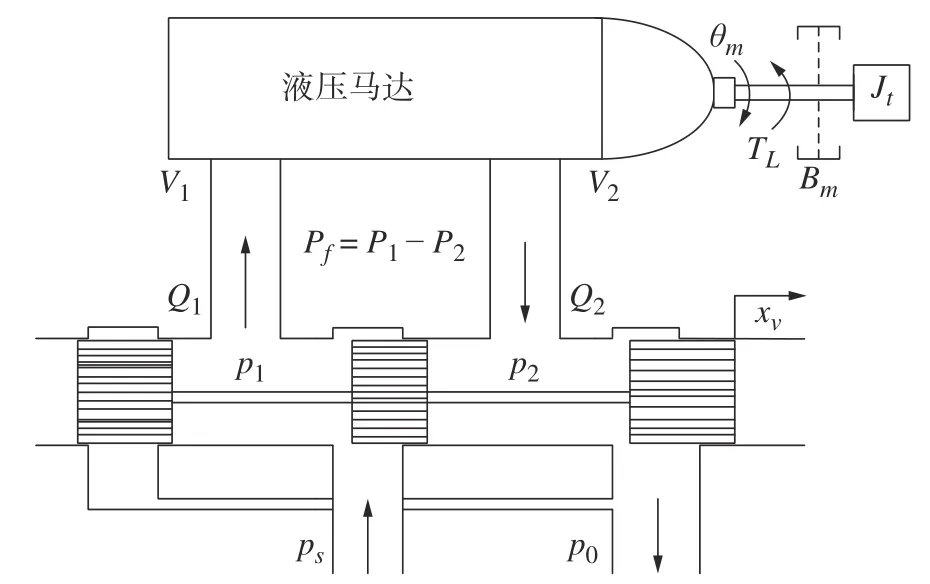
图4 电液伺服阀的原理图Fig.4 Schematic diagram of electro-hydraulic servo valve

电液伺服阀控制液压马达传递函数为

式中Kce=Kc+Ctm

由于台架是非弹性负载，则G=0，另外液压马达和负载的总粘性阻尼系数Bm非常小，故所以得简化的传递函数为

3.4 角度控制回路模型建模

系统角度的控制回路由电液伺服阀、液压马达、蜗轮蜗杆机构、角度传感器、编码器等组成，控制钢索传动装置各安装点的转动角度[8]。其数学模型如图5 所示。

图5 角度控制回路模型Fig.5 The closed-loop control model of system angle

3.5 位移控制闭环回路建模

位移控制回路由电液伺服阀、液压马达、蜗轮蜗杆机构、滚珠丝杠等组成。控制丝杠的升降速度，进而控制钢索传动装置各安装点的升降速度[9-10]。其数学模型如图6 所示。

图6 位移控制闭环回路模型Fig.6 The closed-loop model of displacement control

3.6 阀控系统稳定性分析

机翼弯曲模拟系统的升降位指标：-800～+2 000 mm，角度范围：为 -30o～ +30o。系统的稳定性是系统正常工作的首要条件，根据开环传递函数的伯德图进行稳定性分析。电液位置伺服系统的传递函数[11]为

将参数代入公式（4）中，并通过MATLAB 仿真，得到阶跃响应曲线和伯德图如图7 和图8 所示。

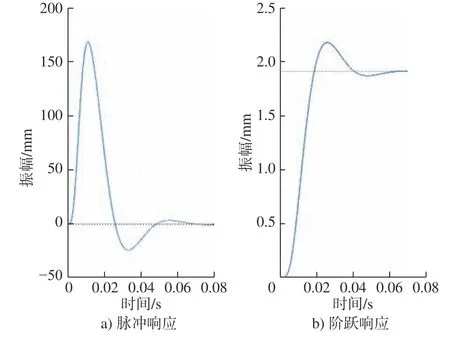
图7 阶跃响应图形Fig.7 Step response graph

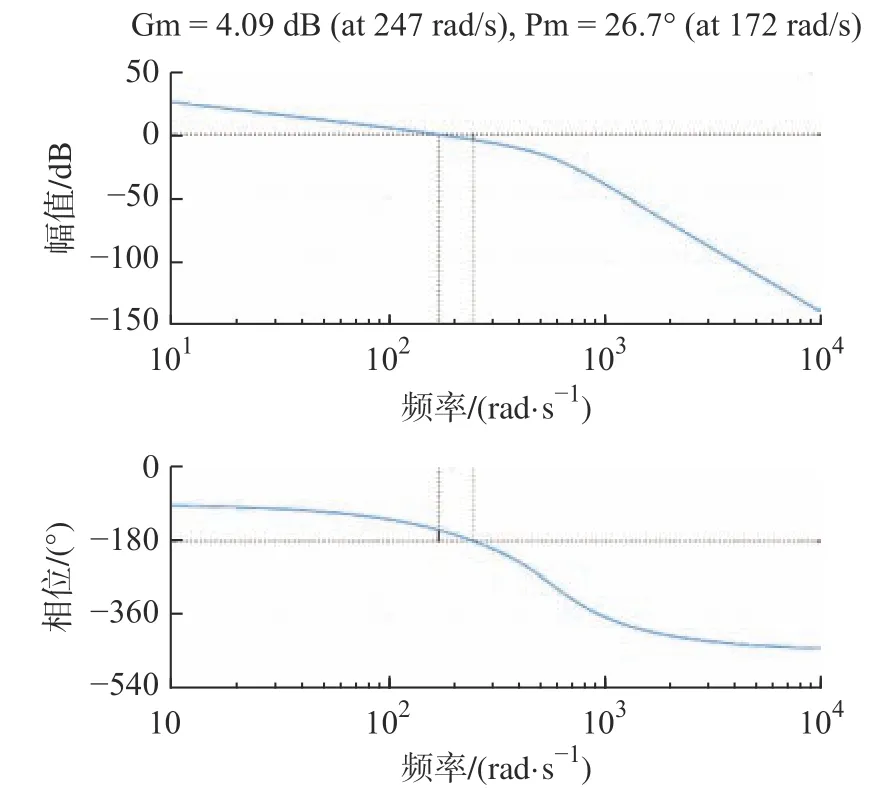
图8 伯德图Fig.8 Bode diagram

开环传递函数的相角裕度与幅值裕度都为正，系统是稳定并且留有一定的相角裕度与幅值裕度，但是相角裕度过于大，故系统的响应时间慢，调节时间长。此系统为I 型系统，对于阶跃信号的输入没有稳定误差，输入信号是斜坡信号时存在稳态误差，可以增加系统的型别来消除稳态误差[12]。

4 前馈补偿模糊自适应控制器

在机翼弯曲模拟系统的姿态调整过程中，钢索传动装置会受到很多因素的干扰，单个台架的控制是一个加载系统，16 套台架安装的钢索调节系统相互干扰。减小多余力和提高系统动态性能是控制的重点，文章提出了有效的前馈和模糊控制相结合的控制策略[12]。

4.1 前馈补偿PID 控制器

确定一个可测的干扰变量，设计相应控制算法，提前控制并消除干扰信号的影响。具体控制结构图如图9 所示。

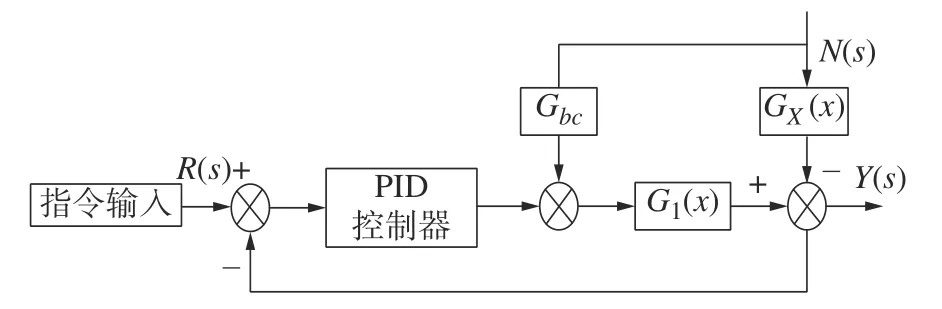
图9 前馈补偿的结构图Fig.9 Structure of feedforward compensation

其中G1（s）为系统的前向通道的传递函数，N（s）为干扰输入，R（s）为系统的给定输入，Y（s）为钢索传动装置的实际输出也就是钢索传动装置在运动过程中过对钢索的力，这个力对其他钢索传动装置而言就是一种干扰[13]，前馈控制器传递函数为Gbc(s)。

4.2 模糊自适应PID 控制器

采用基于神经网络PID 参数自整定控制系统，解决该系统电液控制系统的非线性和时变性等复杂特性。通过对系统性能的学习来确定具有最佳组合的PID 控制参数。模糊算法通过检测e和ec，根据模糊规则来修改PID 参数[14-15]，其结构如图10 所示。

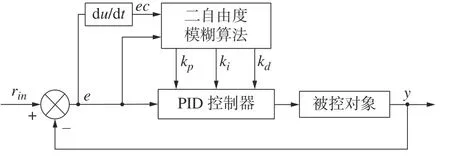
图10 模糊PID 控制算法结构Fig.10 Fuzzy PID control algorithm structure

5 仿真及实验结果研究

最高位试验的变形数据如表1 所示。

表1 钢索传动装置位移量与角度偏移量Tab.1 Displacement and angle offset of the cable transmission device

5.1 仿真结果研究

在系统单路单路电液伺服系统的仿真中，输入正弦波信号： 0.3sin(2πt)+0.6，两种控制策略下（常规PID 控制和模糊自适应PID 控制），的跟踪误差曲线如图11 所示。

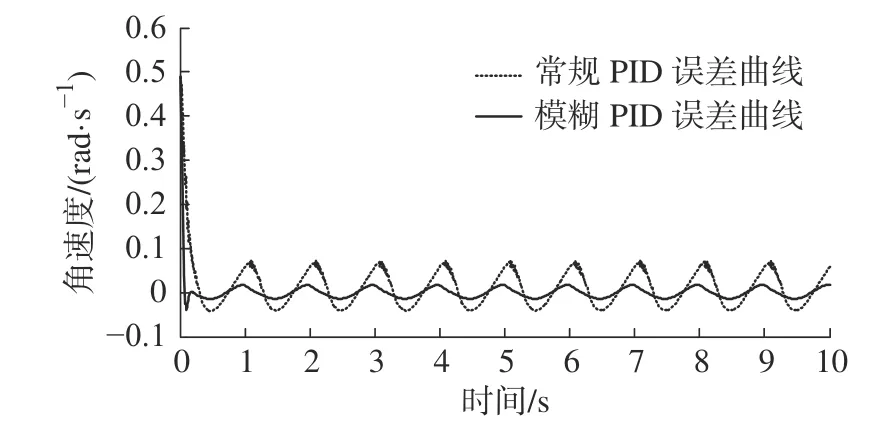
图11 钢索传动装置角速度误差跟踪曲线Fig.11 Angular velocity error tracking curve of the cable transmission device

可以看出：模糊自适应PID 控制器具有响应快、动态性能好、抗干扰能力强等优点[16]。

机翼弯曲模拟系统需要同步控制多路，中文章选用3 个控制回路来做仿真，仿真结果如图12 所示。

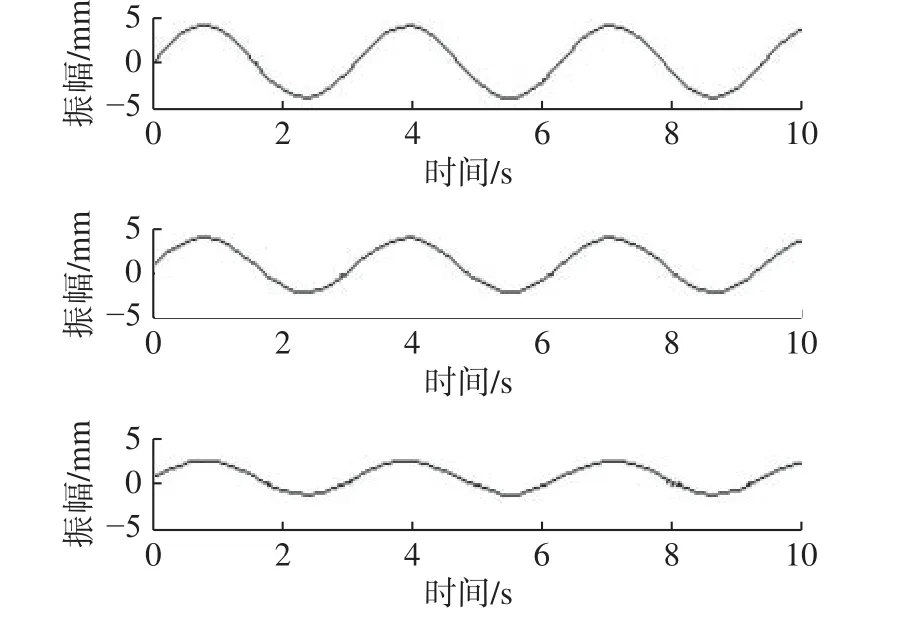
图12 三路同步控制响应曲线Fig.12 Response curve of three-way synchronous control

从图12 中可以看出：三路钢索传动装置响应曲线对于时间轴几乎是同步的，稍微又点滞后和误差，满足技术指标要求。

5.2 试验结果研究

机翼弯曲模拟系统在实际实验中，16 套台架控制的钢索安装点的位移和角度变化较大，最高位试验的变形数据如如图13 所示。

图13 最高位试验结果图Fig.13 Test results at the highest position

图中所有钢索传动装置指示灯均为绿色表示该姿态在目标值允许的误差范围内，最高位试验从零点到最高点总耗时36 min，符合指标要求。在高位试验的过程中[17]，最高位16 号钢索传动装置位移和角度变化的曲线如图14 与15 所示。

图14 最高位试验16 号钢索传动装置位移曲线图Fig.14 Displacement curve of No.16 cable transmission device in the highest position test

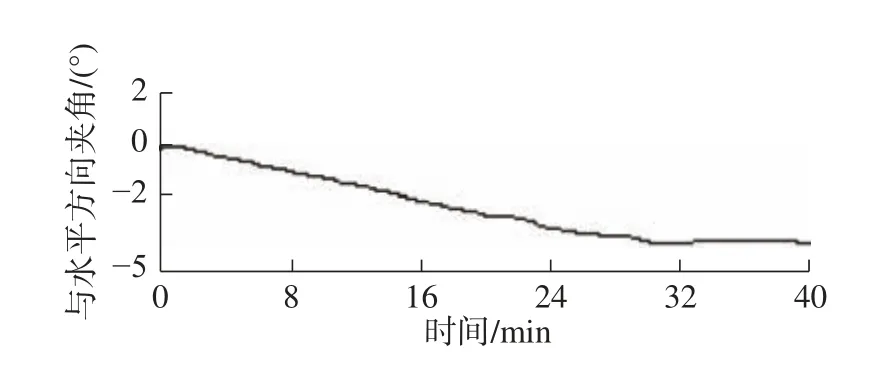
图15 最高位试验16 号钢索传动装置角度曲线图Fig.15 Angle curve of No.16 cable transmission device in the highest position test

5.3 归零试验

归零试验实在系统做完一定变形试验恢复到零点的过程，每个钢索传动装置位移和角度都恢复到零，此处不在一一列出数据表。图16 为归零试验的结果图。从最高位恢复零点的试验中，由于误差的原因最终值均在零点以上，但所有钢索传动装置指示灯均为绿色表示该姿态在目标值允许的误差范围内，从最高位到零点受到钢索传动装置自重的影响，总共耗时25min，这也符合指标要求，在这里我们以钢索传动装置16 为列子看看在整个过程中的曲线变化[12]。图17、图18 分别是从最高位归零位试验中16 号钢索传动装置的位移和角度变化的曲线变化图。