基于特征优化和BSO-RBF神经网络的NOx浓度预测模型

2024-03-20张国兴王世朋

计量学报 2024年2期

张国兴, 王世朋

(国能宁夏鸳鸯湖第一发电有限公司，宁夏银川 750011)

1 引言

目前以煤炭为燃料的火力发电仍为我国发电的主要方式,而发电过程中氮氧化物(NOx)的排放又是大气中的NOx污染的主要源头之一[1]。为控制燃煤电厂发电过程中NOx的过量排放,减少大气污染,我国大多数电厂采用的是氨催化的选择性催化还原技术(SCR)对锅炉燃烧烟气进行脱硝,其效率可达90%以上。因锅炉燃烧过程运行工况复杂,反应延迟较大,致使SCR入口NOx浓度无法准确即时地测量,导致SCR反应过程中因喷氨量少使得NOx无法完全反应或者氨逃逸的现象发生[2]。故建立精准高效的预测模型以满足对NOx排放浓度的实时监测具有重要意义。

模型预测精度好坏有多个影响因素,其中,建模方法的选择是主要影响因素之一。近年来,人工智能的蓬勃发展使得神经网络成为数据建模的重点,Li等[3]利用支持向量机(support vector machine, SVM)建立了NOx排放预测模型,实现了对氮氧化物排放的实时监测;Fu等[4]利用长短期记忆网络(long short-term memory, LSTM)建立了脱硫效率预测模型,预测精度较高。对模型进行超参数优化,可以进一步提升模型的训练效率和预测精度,单斌斌等[5]利用改进天牛须算法优化极限学习机(extreme learning machine, ELM),加快了模型预测时间,提高了模型预测效率;李沁颖等[6]利用粒子群算法(particle swarm optimization, PSO)获得滑模控制器的最优参数,提高了控制器的响应和精度。

锅炉燃烧系统具有大迟延,大惯性的特点,因此对模型输入变量进行时延补偿尤为必要。闫来清等[7]采用K近邻互信息计算时延的方法对各输入变量进行重构后再放入模型进行预测,提升了模型预测精度;唐振浩等[8]利用Pearson相关系数法对各输入变量进行时延性分析重构,重构后的变量输入模型后使得预测结果有了较大的提升;吴康洛等[9]采用最大互信息系数(maximal information coefficient, MIC)估计各变量迟延时间对数据进行重构,提升了模型的预测精度。Hong等[10]利用主成分分析法(principal components analysis, PCA)对变量进行降维重构,提高了模型效率,但破坏了数据本身的信息;刘岳等[11]利用索套算法(least absolute shrinkage and selection operator, LASSO)去除了输入之间的冗余变量,精简了模型结构,但没有考虑输入变量对原始变量的影响,Qiu等[12]利用经验模态分解(empirical mode decomposition, EMD)对数据进行重构,提炼了数据深层的时域和频域信息;谢丽蓉等[13]利用集合经验模态分解(ensemble empirical mode decomposition, EEMD)将风功率信号分解后进行相空间重构,实现了特征优化提高了预测精度。

本实验采用互信息算法对各变量与输出之间进行时延补偿计算,再将加入时延补偿的变量放入模型进行预测。同时,输入变量的选择也会直接影响到模型预测结果,此外还使用K近邻算法对初始变量进行特征选择,使用互信息变化率的原理,消除冗余变量的同时也考虑到了加入数据对原始数据的影响。但筛选出来的原始数据其中包含了较多的噪声及非平稳性较高的信息,通过变分模态分解并选择最终输入变量,最后采用BSO优化后的RBF对NOx浓度进行预测。在此过程中,设计了一系列相关实验,以验证各环节的有效性。

2 基本原理及实验设计

2.1 K近邻互信息变化率

K近邻互信息(K-nearest neighbor-mutual information, KNN-MI)采用的是计算样本之间的欧氏距离[14]。假设样本输入集D={x1,x2,…,xm},输出为Y,其中xi=[xi1,xi2,…,xin]T,设Z为向量空间上面一点,Z=(xij,yj),其它点Z′到点Z的距离为:

I(x,y)=ψ(K)-〈ψ(nx+1)+ψ(ny+1)〉+ψ(n)

式中:K取值范围2～6;ψ为伽马函数;n为变量个数。

由低维K近邻互信息类推到高维K近邻互信息,式为:

I(x1,x2,…,xm,Y)=ψ(K)-<ψ(nx1)+ψ(nx1)

+…+ψ(ny)>+mψ(n)

式中:m为输入变量维度。

变化率[15]式如下:

(1)

当一组变量中加入新的变量di后,如果di是不相关的,则变量的不确定性就会变大。因此,如果加入变量di是相关的,则K近邻互信息变化率就会变小。由此可得,通过K近邻互信息变化率可以对变量子集进行初步前向选择,既考虑到了高维变量之间的互信息,又考虑到了加入新的变量后对初始变量的影响。所选出的变量子集有可能会存在某几个变量之间冗余的情况,所以通过计算所选变量之间的一维互信息可以删除冗余变量。基于K近邻互信息变化率的双向变量选择(K-nearest neighbor mutual information change rate, KNN-MI-CR)步骤如下:

1)前向选择。设置初始变量子集S,此时S为空集;计算输入变量子集D内任一变量xi与输出Y之间的一维互信息值,并由大到小排列,取互信息值最大的变量放入S集中,作为初始变量。

2)按照步骤1)中剩余输入变量子集D的顺序依次代入式(1)计算R(S+di,Y)的大小;设置阈值α=0.1,选取R<0.1所对应变量加入S集中。

3)重复步骤2),直至所有变量被选取完毕,形成初始变量子集S。

反向选择:计算S集中任意2个变量之间的一维K近邻互信息值,选取互信息值较大变量组合作为冗余组合,并以步骤1)中所计算的与输出变量Y之间的互信息值为参照,删除冗余变量,形成最优变量子集S。

2.2 变分模态分解

变分模态分解(variational mode decomposition,VMD)是一种完全非递归的信号处理方法[16]。VMD可以较好的抑制EMD存在的模态混叠问题,能够有效地处理非平稳、非线性序列。提前设置分解个数K,根据信号自身特性,VMD算法可以自适应地将信号分解为K个具有不同中心频率的固有模态分量(intrinsic mode function, IMF)。VMD算法分解过程主要包含对变分约束问题的建模和求解2个部分,具体分解步骤详见文献[17]。

2.3 RBF神经网络

径向基神经网络(radial basis function, RBF)是一种具有单隐层的三层前向神经网络,包括输入层、隐含层和输出层[18]。RBF神经网络结构简单,收敛效果好,能够逼近任意非线性函数,具有逼近能力强,学习速度快的显著优点。其基本思想就是使用RBF作为隐含层单元的基构成隐藏层空间,进而对输入矢量进行变换,将数据转化到高维空间,使得线性不可分问题在高维空间线性可分。

2.4 基于天牛须改进的粒子群算法

2.4.1 天牛须搜索算法

天牛须搜索算法(beetle antennae search,BAS)是由Jiang等[19]在2017年提出的一种智能优化算法,属于启发式算法的一种。该算法通过模拟自然界中天牛寻食这一现象,来达到快速搜索的目的,是一种单体搜索的算法,具有结构简单、计算量少等优点,在处理低维优化目标时具有非常大的优势。

天牛须搜索算法具体步骤如下:

1) 初始化天牛。设置天牛初始质心位置为x,左须为xl,右须为xr,两须之间的距离为d0,维度为k,步长为Nstep,算法迭代次数为n。由于天牛头的朝向是随机的,所以其初始方向为Dir。

Dir=rands(k,1)

式中:rands为k维随机变量,数值在0～1之间。

2) 计算左右须位置。将方向归一化后,通过式(2)计算左右两须位置。

(2)

3) 更新天牛位置。计算天牛左右两须的气味感知强度,即计算左右两须的适应度函数值,再将左右函数值的大小代入式(3)来更新天牛位置。

x=x-Nstep×Dir×sign(f(xl)-f(xr))

(3)

式中:f(xl)、f(xr)为天牛左右两须的适应度函数值;sign为符号函数,用来表示值的正负。

4) 更新迭代。其中,天牛两须之间的距离d0通过式(4)迭代更新,移动步长Nstep通过公式(5)迭代更新。

d0=Nstep/c

(4)

Nstept=λNstept-1

(5)

式中:c为固定值,取100;λ为衰减系数,通常取0.95。

5) 判断是否到达迭代次数或满足停止迭代要求,若没有,继续迭代直至结束。

2.4.2 基于天牛须改进的粒子群算法

天牛须算法会随着迭代次数的增加,移动步长逐渐衰减,导致陷入局部最优。将天牛须搜索算法与更突出群体的粒子群优化算法相融合[20],提出了基于天牛须改进的粒子群算法(beetle swarm optimization,BSO)。BSO将每个粒子视为一只天牛,天牛群的初始位置和速度的生成过程与标准粒子群算法相同。在迭代过程中,天牛位置的更新增加了天牛须对气味浓度感知的过程,通过比较左右两须的气味浓度即适应度函数值大小来更新天牛的位置。BSO有效克服了BAS中随着迭代次数的增加导致步长逐渐减小从而陷入局部最优的缺点,同时提高了算法整体的稳定性。

BSO更新规则如下:

1) 天牛群速度更新规则。根据天牛须算法得到速度更新公式为:

v0=-Nstep×Dir×sign(f(xl)-f(xr))

将其融入粒子群算法的速度更新公式中得到天牛群算法的速度更新公式为:

v=w×v0+c1×r1×(pibest-x)+

c2×r2×(gbest-x)+c3×r3×v0

式中:w为惯性权重,变化规则为公式(6);c1、c2、c3为学习因子,均取1.2;r1、r2、r3为rand函数;pibest为当前位置个体最优解;gbest为当前位置全局最优解。

(6)

设置速度界限为±0.1,当速度超出边界值时将速度校正为边界值。

2) 天牛群位置更新规则。

xi+1=xi+vi+1

式中:xi+1为第(i+1)次迭代天牛位置;vi+1为第(i+1)次迭代天牛速度。

3) 天牛群步长更新。由于BAS算法迭代过程中步长的衰减系数是固定不变的,这会导致天牛在前期进行搜索迭代时因为步长过长而使得搜索精度降低,后期因为衰减较慢使得搜索效率变差。因此,提出一种动态衰减策略:

式中:Nstep0为初始步长,其大小通常与变量变化范围相等。

BSO算法具体步骤如图1所示。

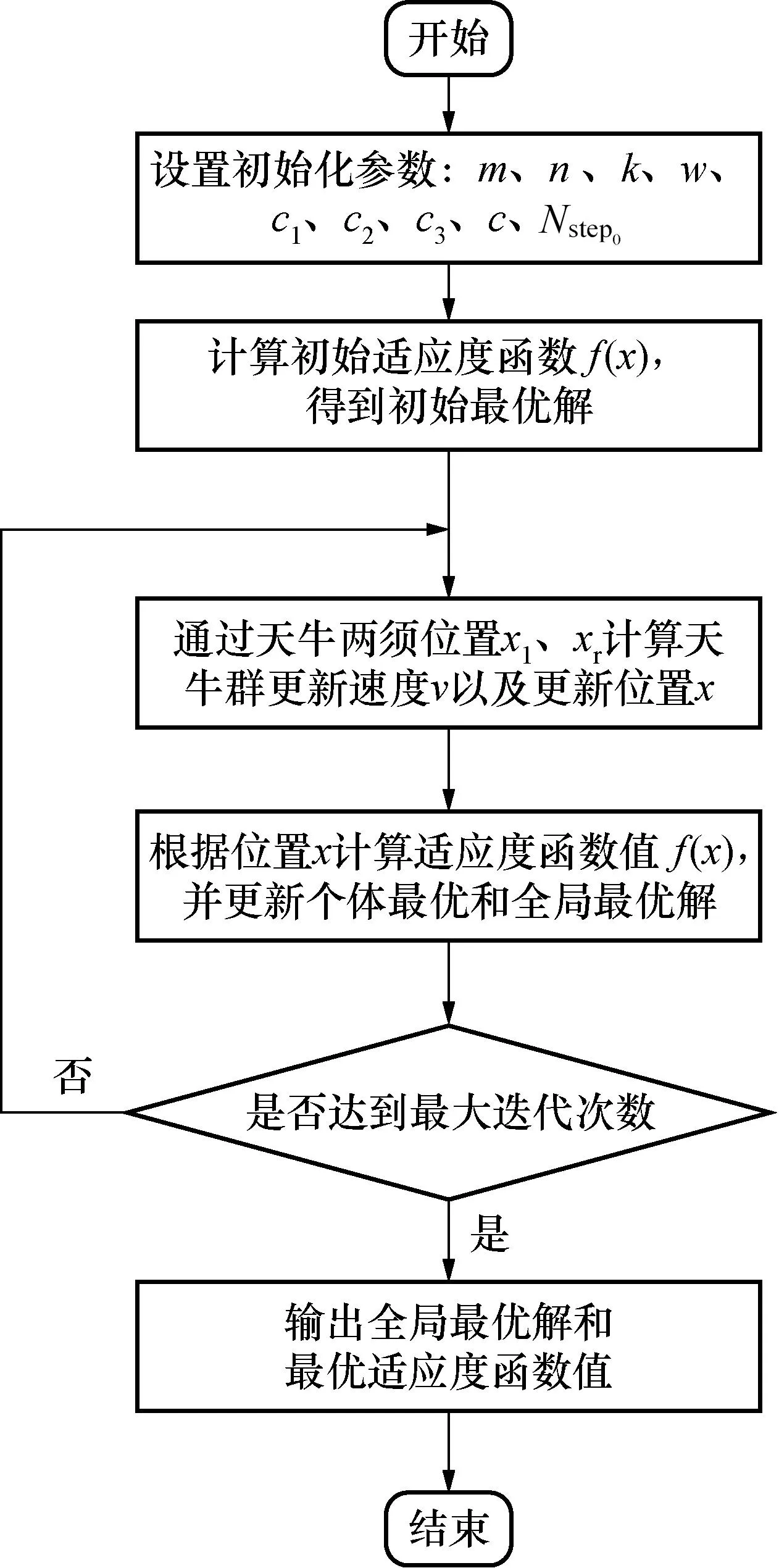
图1 BSO算法流程图Fig.1 BSO algorithm flow chart

2.5 BSO算法性能分析

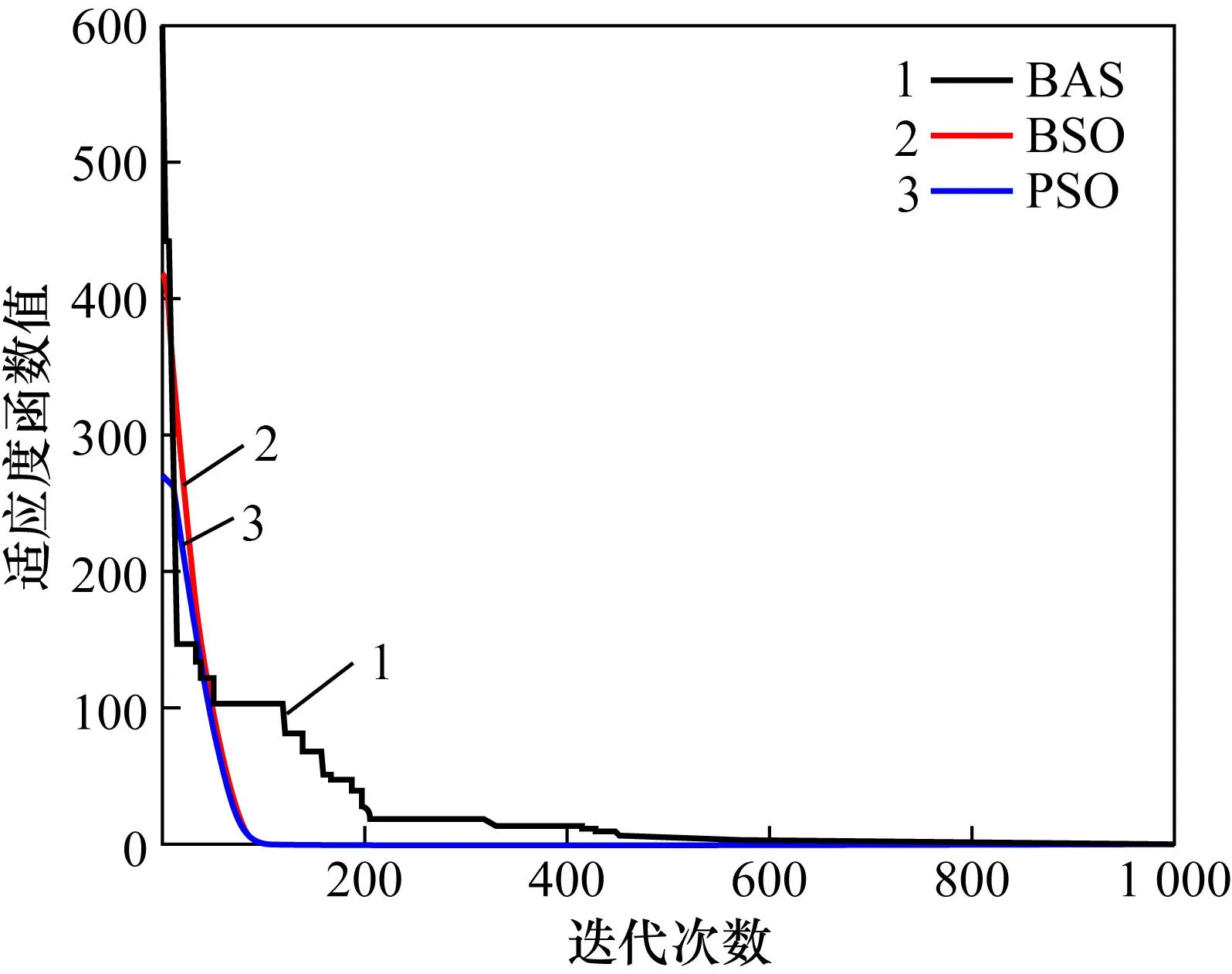
图2 算法寻优结果比较Fig.2 Comparison of algorithm optimization results

表1为算法寻优结果及运行时间。

表1 寻优结果Tab.1 Optimization result

由图3和表1可知,BSO算法的收敛效果明显优于其它2个算法,且算法的稳定性也较高。BSO算法将BAS的全局搜索能力和PSO算法的局部搜索能力相结合,使得算法整体上更加稳定,性能也有明显的提升。

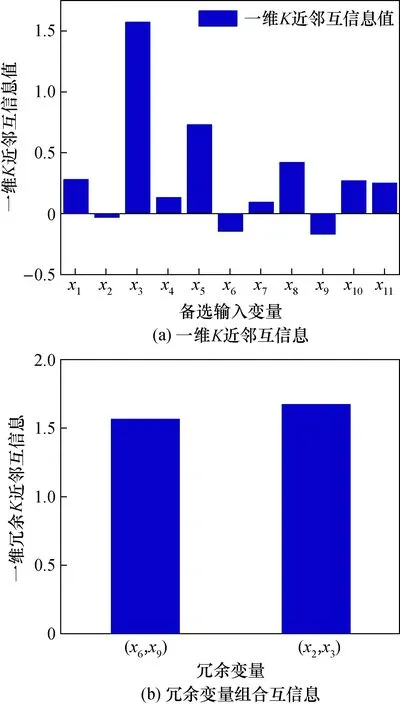
图3 K近邻互信息值Fig.3 K-nearest neighbor mutual information value

2.6 实验设计

建立预测模型具体流程如下:

1)通过机理分析选定11个初始相关变量,并利用互信息相关性对各变量进行时延补偿。

2)使用K近邻互信息变化率双向选择算法对加入时延的11个初始变量进行筛选,去除冗余变量,生成包含5个输入变量的最优子集。

3)利用VMD算法对变量子集进行分解,分解后的28个IMF分量再经过互信息计算与筛选,确定模型的最终输入。

4)搭建RBF神经网络,利用BSO优化算法对神经网络的超参数进行寻优,将数据代入模型中进行训练和测试,得出最终结果。

2.7 模型评价指标

模型采用的评价指标为SRMSE和R2。SRMSE为均方根误差,表示预测值与真实值之间的标准偏差的大小,数值越小表明预测精度越高;R2为决定系数,表示预测值相对真实值的偏离程度,其数值越接近于1表明预测效果越好。将二者结合使用能够更全面的评价预测模型的好坏,计算式如下:

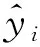
3 变量筛选及实验结果分析

3.1 变量筛选

本文选取某电厂所提供的现场数据共3 600组,采样周期为5 s,总选取时间为5 h。其中前2 400组数据用来对模型进行训练,后1 200组数据用来对模型进行测试,目的为验证模型的预测精度。通过对NOx生成机理进行分析,初步选择出11个辅助变量,包含:机组负荷、总煤量、给煤机电流、SCR入口烟气含氧量、SCR入口烟气温度、总风量、锅炉含氧量、尿素阀门开度、SCR入口烟气流量、炉膛负压、尿素流量。

由于锅炉燃烧过程具有大迟延的特性,所以在现场运行过程中采集到的各个点位的相关数据与SCR入口NOx浓度实时数据存在一定的时间偏差,因此设计了一种基于最大互信息的时延计算方法[21]。根据经验,锅炉燃烧周期为10 min左右,所以将最大时延时间定为600 s。计算方式为固定SCR入口NOx浓度选取时间,将其余所有辅助变量分别向前一时刻移动,每移动一时刻就计算这个时刻辅助变量与NOx浓度之间的互信息值,选取相关性最大的一时刻作为时延补偿,从而确定最终变量输入序列。表2为各变量迟延时间表。

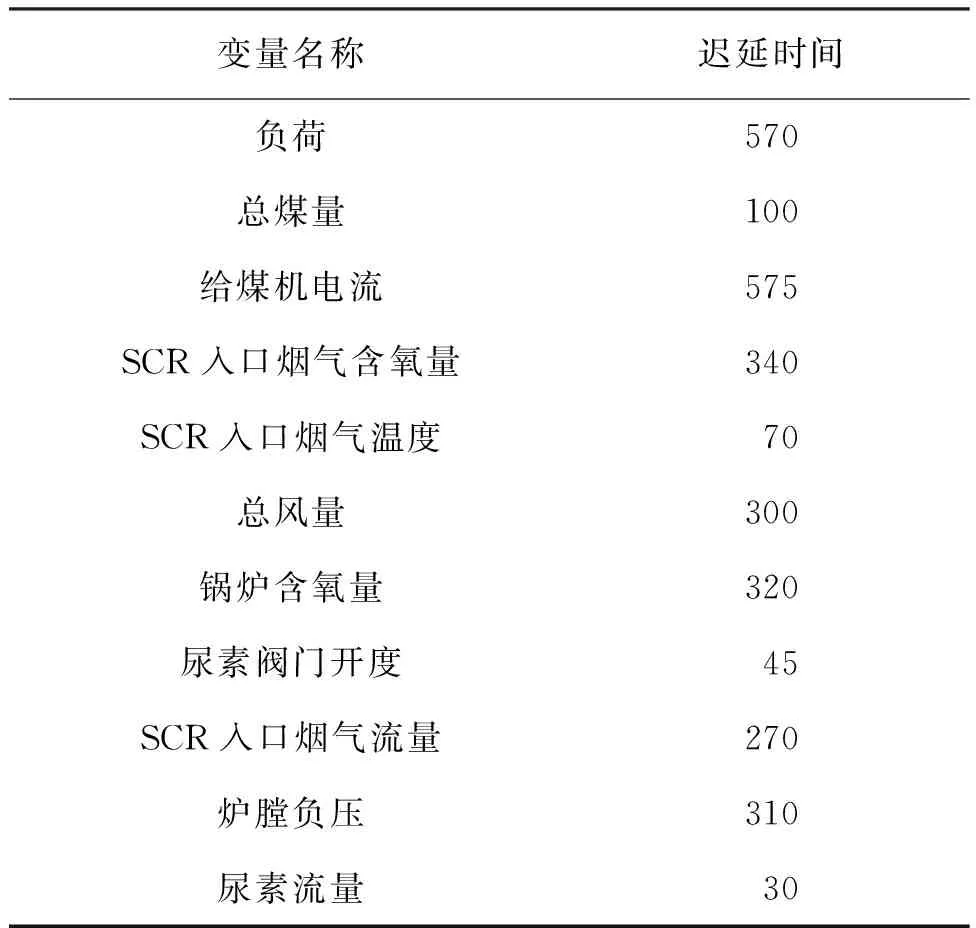
表2 各变量迟延时间Tab.2 Delay time for each variable s

3.1.1 基于K近邻互信息变化率的双向变量选择

通过机理分析选择出来的11个辅助变量之间有可能会存在冗余,而冗余变量输入模型后对模型的预测精度有较差的影响,所以要对这11个初始变量利用KNN-MI-CR进行进一步筛选。将上述11个初始变量按顺序贴上标签,分别为:x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11。图3(a)为一维K近邻互信息计算结果图,由此图可知x3对应的一维K近邻1.56互信息值最大。设置K近邻互信息变化率阈值为0.1,按照2.1流程计算,最终得到初始变量子集S={x1、x2、x3、x4、x6、x7、x9}。图3(b)为集合S内变量之间的K近邻互信息较大的冗余变量组合的互信息,其值均较大,表明x6、x9和x2、x3之间存在冗余变量。根据图3(a)所示:I(x6,y)>I(x9,y),I(x3,y)>I(x2,y),因此x2和x9为冗余变量,剔除之后得到最终输入变量子集S={x1、x3、x4、x6、x7},即给煤机电流、总风量、锅炉含氧量、负荷及SCR入口烟气含氧量。

3.1.2 基于VMD分解的变量处理

经VMD分解后的信号存在多个IMF分量,而分量个数越多意味着表征高频噪声分量的IMF中真实噪声占有比重就越大,所以确定合适的分解个数K能够更好地对信号存在的噪声进行分离。本文通过计算原始信号信噪比(signal noise ratio,SNR)[22]并与设定阈值相比较来确定分解个数K,SNR计算公式如下:

(7)

式中:f为不带噪声的原始信号,即原始信号与高频IMF分量只差;f′为噪声信号。

设置VMD分解算法中惩罚因子α=2 000,根据式(7)计算并选择合适分解个数K。表3为子集S内各变量分解个数及分量选取结果。

表3 变量分解个数及分量选取结果Tab.3 Factorization number of variables

分解后得到28组IMF分量,计算各分量与输出变量之间的互信息值,选择互信息大于0.85的10组分量作为最终输入变量。VMD分解后确定输入变量的时域波形图如图4所示。

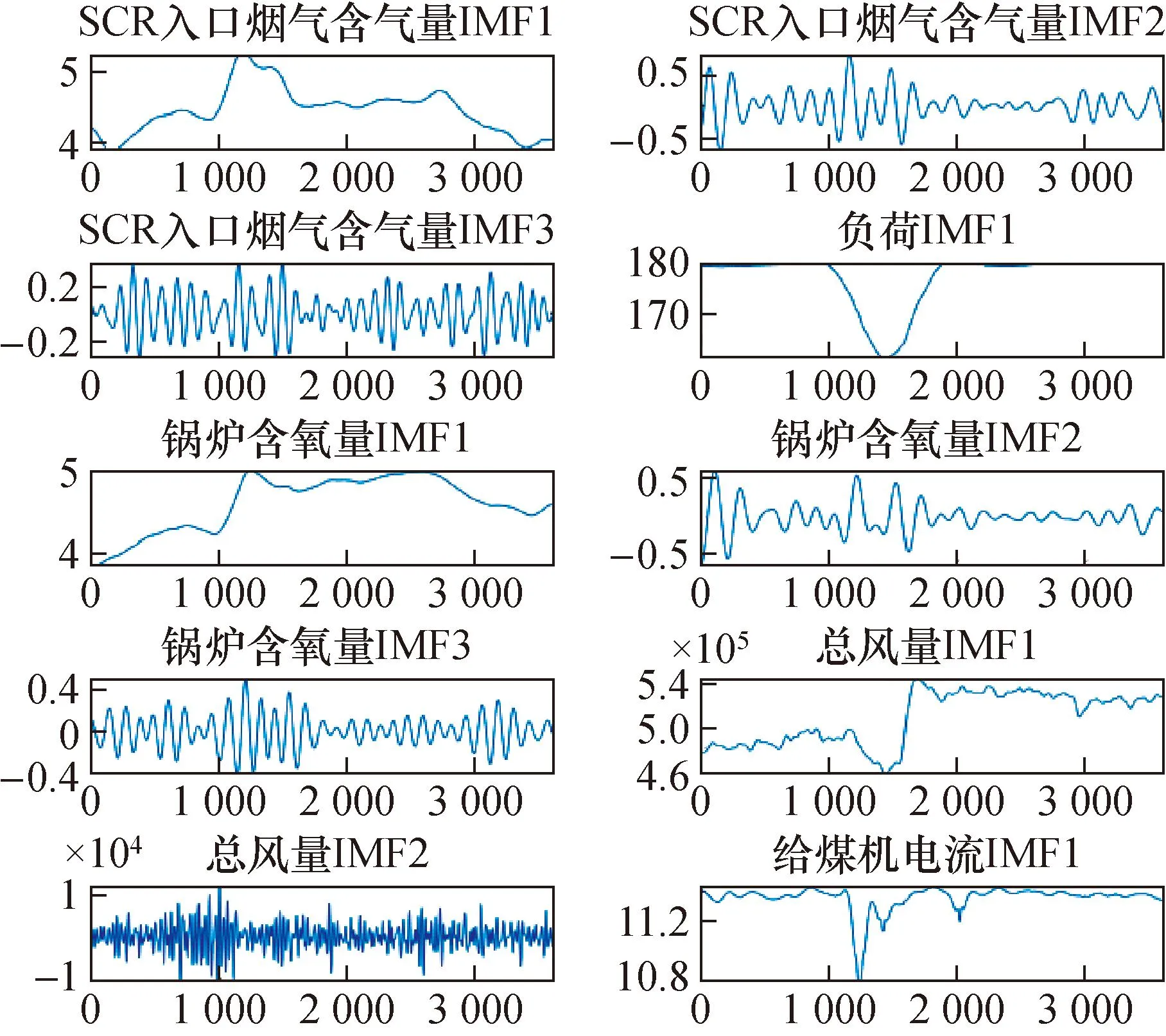
图4 信号时域波形图Fig.4 Signal time-domain waveform

3.2 实验结果分析

3.2.1 不同特征选择方法对预测结果的影响

为验证基于KNN-MI-CR算法对变量筛选的优劣性,现对11个初始变量利用最大相关最小冗余(max-relevance and min-redundancy, mRMR)[23]和随机森林(random forest, RF)[24]这2种特征选择的算法重新进行变量筛选,以对比3种不同方法之间的预测结果,实验条件均相同,筛选变量个数均设置为5个。图5为不同特征选择算法下的预测结果散点图。

图5 不同特征选择预测结果散点图Fig.5 Different feature selection prediction results scatter plot

由图5可知,经过KNN-MI-CR算法筛选后的模型输入变量预测结果更加接近于真实值曲线,跳跃点较少,且各模型评价指标也均优于其它2种算法,这表明使用KNN-MI-CR算法可以更好地选择与输出最相关变量以及剔除冗余变量。其中,不经过变量筛选的初始变量集代入模型后的预测结果相比于经过筛选变量后的明显较差,模型评价指标均差于其它变量输入预测结果,所以模型输入变量的筛选可以有效地提高模型预测精度,同时可以缩减模型的计算时间。

3.2.2 时延分析对预测结果的影响

锅炉燃烧系统是一个大迟延系统,各变量之间的时间延迟对结果也会有一定程度的影响。现将输入变量固定,分别将考虑时延分析与不考虑时延分析的输入变量放入同一个预测模型,得到结果如图6 所示。结果表明,考虑时延分析后的输入变量使得模型预测结果SRMSE降低了40.6%,R2提高了2.15%,可见考虑时延分析后的输入变量增强了与输出变量之间的相关性,对模型预测精度的提升有较大作用。

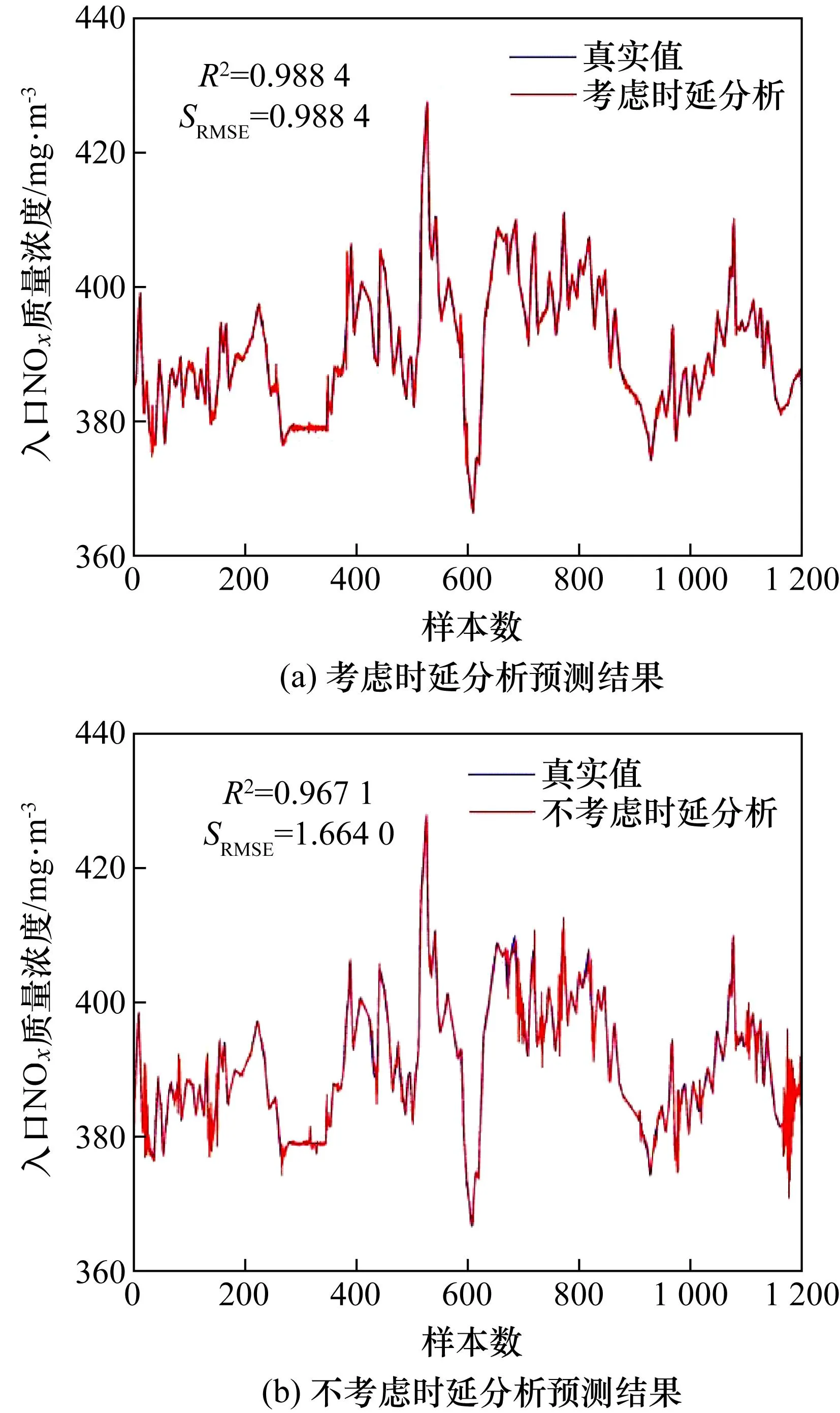
图6 时延对比结果曲线图Fig.6 Time delay comparison curve

3.2.3 变量处理对预测结果的影响

原始数据会存在一定的非平稳性和噪声量,利用VMD分解可以提取数据中的平稳分量,去除噪声。为了验证VMD算法对模型预测的影响,现将变量分解前的输入变量和VMD分解后的筛选变量放入同一模型内进行预测,隐含层神经元个数均设为输入维度的1.5倍,其余条件均保持不变,预测结果图及模型评价指标结果如图7所示。由结果可知,VMD分解后的变量输入模型后的预测结果优于分解前,各评价指标也较好。表明VMD分解可将原始数据中非平稳性较高的数据分解为多个平稳分量以及噪声分量,互信息算法再将非平稳度较高和噪声分量剔除,只保留了相关性较大的平稳分量,有效地提升了模型的预测精度。

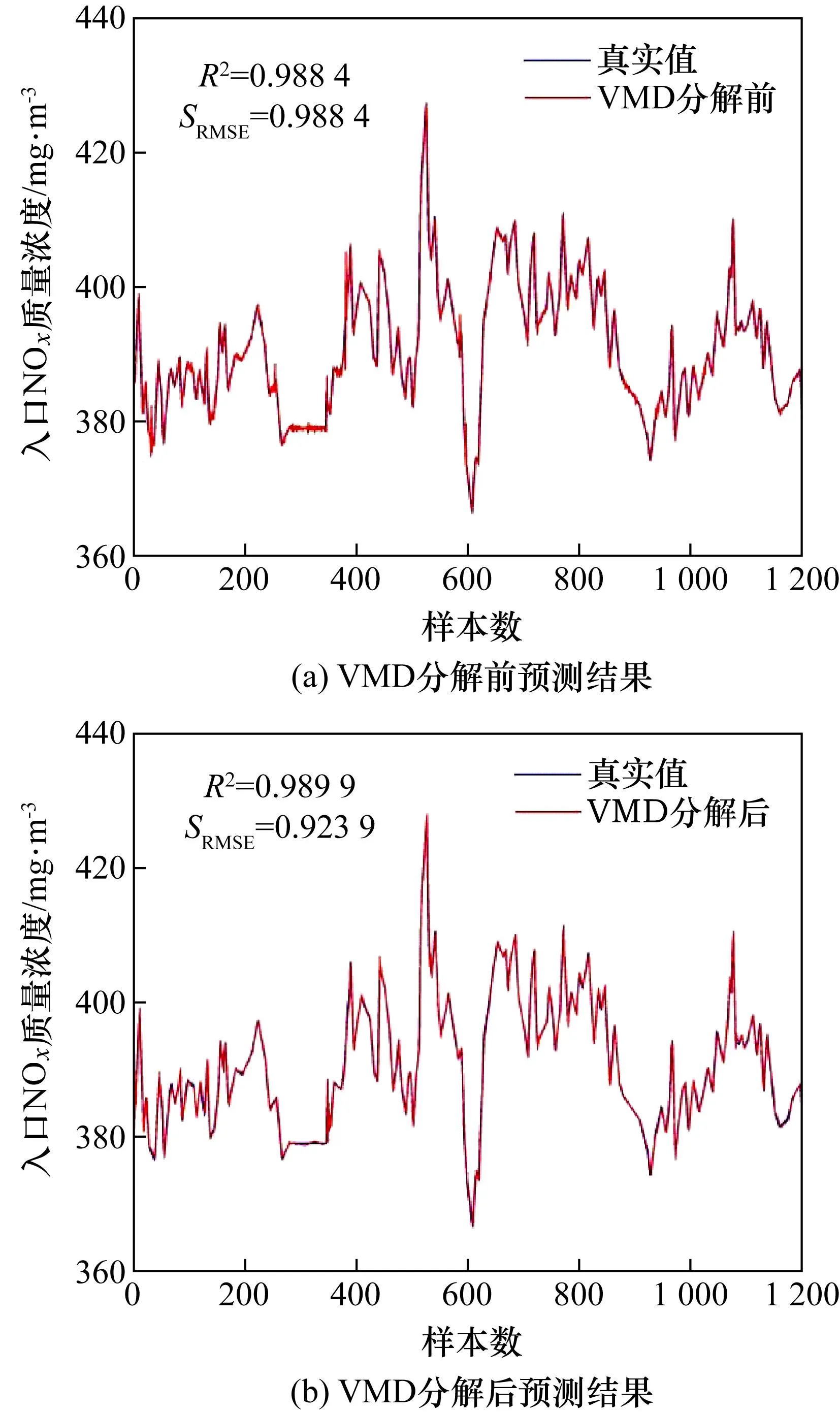
图7 变量分解前后预测结果比较Fig.7 Comparison of prediction results before and after variable decomposition

3.2.4 不同寻优算法对预测结果的影响

RBF神经网络超参数包括:u、σ、w,不同寻优算法获得的模型参数精度不同,从而使得模型预测结果也是不同的。现使用BAS算法、PSO算法、BSO算法作为寻优算法分别对RBF神经网络超参数进行寻优,其中,PSO与BSO种群规模均与输入维度相等,RBF隐含层神经元个数为输入维度的1.5倍,实验结果如图8所示。由图8可知,BAS算法与PSO算法预测结果SRMSE相差不大,且R2仅相差0.000 1,BSO算法的预测结果优于其余两种算法。预测过程中,BAS算法多次预测时预测结果上下浮动变化较为明显,这与其只有一个寻优粒子使得其稳定性较差有关。结果表明BSO算法在提高模型预测精度上要优于BAS和PSO算法,且寻优过程较为稳定,多次预测依然保持较好效果。