基于BA-MKELM的微电网故障识别与定位

吴忠强, 卢雪琴

(燕山大学 工业计算机控制工程河北省重点实验室，河北 秦皇岛 066004)

1 引 言

近年来,随着电力电子技术的进步和环境意识的逐渐增强,分布式能源以微电网的形式向传统配电系统不断渗透,改变了配电系统的结构,带来了诸多好处。如分布式电源和负荷(供热和电力)的距离减小降低了运行成本,减少了输电线路的损失,改善了电能质量;微电网的运行模式较为灵活,当电网受到扰动或中断时能够独立工作,提供不间断供电,有助于减少停电的持续时间和频率,提高了电力效率和传统配电系统的稳定性和安全性[1,2]。然而随着微电网规模不断扩大,其内部线路故障发生的频率逐渐增大。在微电网运行过程中,若出现故障未及时进行诊断和处理,会影响系统的稳定运行,严重时会导致大电网崩溃,造成严重的经济损失[3～5]。因此,提高微电网线路故障诊断的准确性和实时性对电力系统稳定运行具有重要的现实意义。

传统的配电网故障诊断方法不适用于拓扑结构多变、运行方式灵活的微电网,因此需要一种更加智能、可靠的故障诊断方法来识别和定位微电网故障。目前,国内外对微电网故障识别和定位的研究已取得了一定成果。文献[6]提出一个数学模型,通过量化故障检测的界限避免造成盲目跳闸,但是,该方法的性能并没有在测量不确定度下进行验证。文献[7]提出了一种基于正序和零序电压相角和幅度的故障诊断方法,但是,故障分类阈值的选择缺乏自适应性。文献[8～10]提出了一种基于阻抗的故障定位方法。然而,当配电线路较短,配电系统存在分布式能源和支路,且故障电阻未知时,这些方法并不适用。文献[11～13]采用小波变换和神经网络相结合对微电网线路故障进行诊断,提高了故障识别的准确性。然而由于神经网络对初始参数依赖性较强,参数选取不当会严重影响诊断精度。在文献[14～16]中,数字信号处理方法和深度学习的组合被应用于微电网的故障检测、分类和定位中。然而深度学习需要大量的训练数据,当数据样本不足时,识别和定位结果会出现较大偏差,同时网络结构复杂,在处理数据时也存在计算速度方面的不足。

本文提出一种基于贝叶斯算法(Bayesian algorithm,BA)优化多核极限学习机(multi-kernel extreme learning machine,MKELM)的微电网故障识别和定位方法,首先根据小波包变换将采集到的微电网三相故障电压信号进行分解,提取部分故障特征组成特征向量作为网络输入;其次,针对ELM输入参数和隐含层节点数随机选取导致回归能力不足的问题,引入核函数,将多项式与高斯径向基核函数加权组合构成MKELM建立故障识别和定位模型;最后,为了进一步提高模型的逼近能力,利用BA对MKELM相关参数进行优化得到BA-MKELM诊断模型。BA全局寻优能力强,可通过较少的迭代计算快速准确地找出全局最优值,有利于进一步提高模型的学习速度、识别和定位精度。

2 BA

BA是一种不需要使用梯度信息即可对黑箱函数进行全局优化的有效方法,其速度快、效果好[17]。该算法通过学习与需要优化的数据一致的函数分布来形式化优化问题,通常采用高斯过程作为概率模型来捕获未知函数。

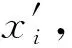
(1)

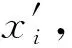
(2)

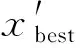
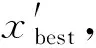
采集函数有很多种,也可以选择“改进概率PI(probability of improvement, PI)”或者“低置信界BLC(lower confidence bound, LCB)”类型。PI是由一个新的x′得到一个较低目标函数值f(x′)的概率,f(x′)经过m改进,其数学表达式为:

(3)

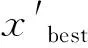
BLC的采集函数是后验均值与两个标准偏差的差值的最大值,定义如下:

BLC(x′)=max(μQ(x′)-2σQ(x′))

(4)

式中:μQ为后验均值;σQ为后验标准偏差。

3 BA-MKELM模型

3.1 MKELM

极限学习机(extreme learning machine,ELM)是一种新型的非迭代学习方法,克服了基于梯度的学习算法所面临的问题,与BP神经网络、RBF神经网络等算法相比,ELM训练速度更快、逼近能力和泛化能力更强,其网络结构图如图1所示。

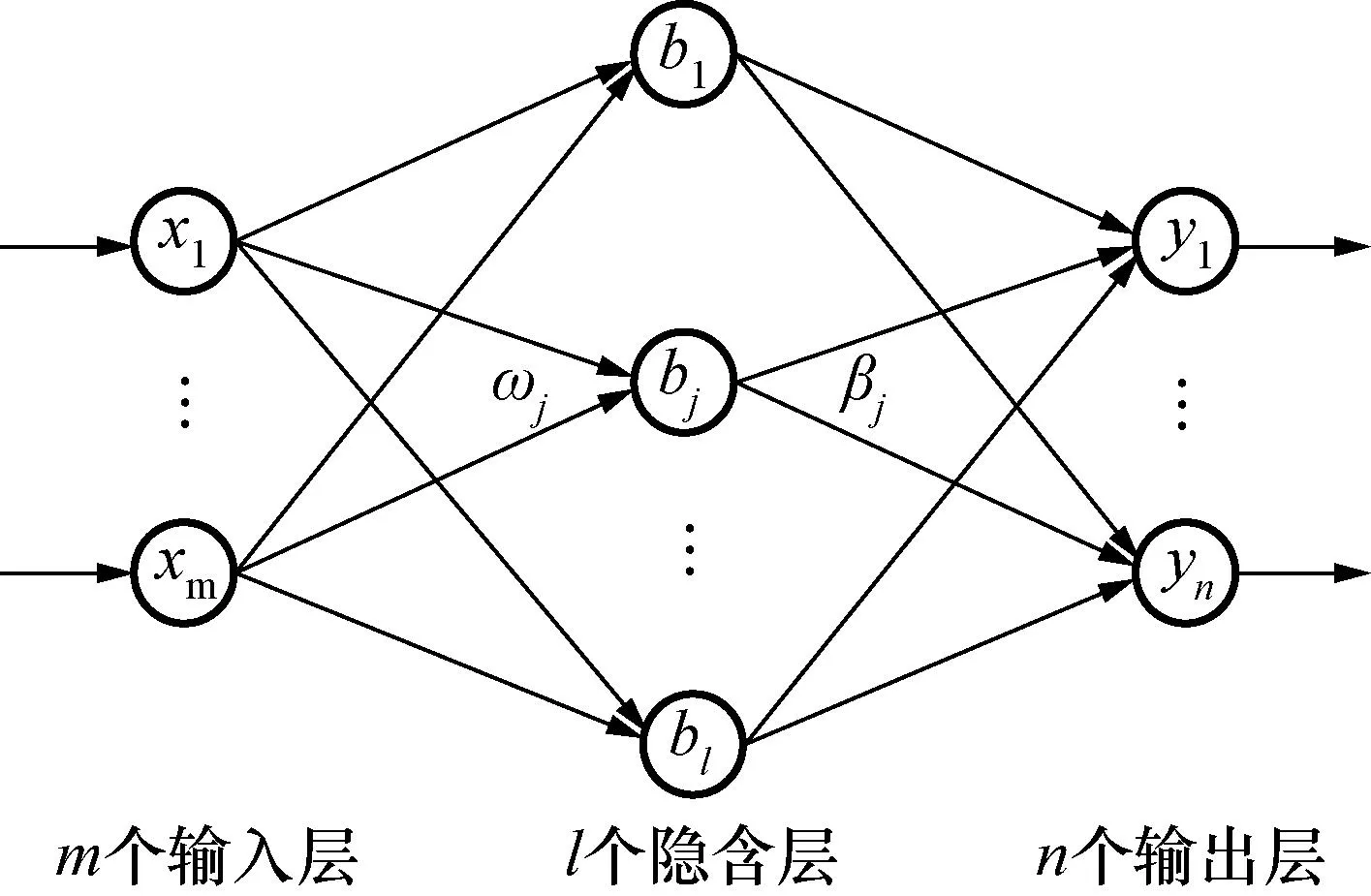
图1 ELM网络结构图Fig.1 Structure diagram of ELM

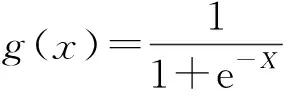
Hβ=Y

(5)

(6)

式中:H为隐藏层神经元的输出矩阵;β为隐藏层到输出层的权值矩阵;Y为网络目标期望输出矩阵。输出权重β可通过求解隐含层输出矩阵H的广义逆矩阵,并根据式(7)得到:

β=H+Y

(7)

ELM与其它传统神经网络相比,在训练速度和效果方面性能更好,对未知数据的预测能力和逼近能力更强,但是其仍存在一些缺陷,如网络中间隐藏层的节点个数难以确定;输出权重β通过求逆得到,未加入正则化,仍可能出现过拟合现象。针对这些问题,文献[19]提出一种核极限学习机(kernel extreme learning machine ,KELM)网络,KELM是受支持向量机的启发,在网络隐层中使用核函数的方法。与极限学习机相比,核极限学习机能够得到最小二乘优化解,具有更好、更可靠的泛化能力。核矩阵K(X)可定义为:

K(X)=h(X)·HT

(8)

k(xi,xj)=h(xi)·h(xj)

(9)

式中:h(X)为隐层特征映射,通常是未知的;k(xi,xj)是核函数K(X)中第i行第j列元素。

对于给定的输入X,输出Y,则KELM网络的预测输出可表示为:

y=h(X)·HT(K(X))-1·Y

(10)

加入正则化后:

(11)

式中:C为正则化系数。

根据核函数是否具有平移或者旋转不变性,可以将核函数划分为两种不同的类型:局部核函数和全局核函数[20]。局部核函数擅长提取数据样本的局部特征,对于分布相对集中的故障数据样本,其诊断精度较高,具有很强的学习能力,但是对未知数据的预测和逼近能力较弱;而全局核函数擅长提取数据样本的全局特征,对分布相对分散,距离较远的故障数据样本的诊断精度更高,对未知数据的预测和逼近能力较强,但是在学习能力方面表现较差。

在KELM的隐层中使用由不同核函数线性组合所得的混合核函数可得到MKELM。平衡参数为λn的混合核函数数学表达式如式(12)所示。

(12)

由于不同核函数对故障数据样本会给出不同的相似性度量,因此不同的核函数在相同的故障数据样本集上的性能可能存在较大偏差。本文在综合考虑各核函数的基本特性和计算复杂度的基础上,选用多项式和高斯径向基核函数组合来研究微电网故障识别和定位问题:

k(xi,xj)=λk1(xi,xj)+(1-λ)k2(xi,xj)

(13)

式中:λ为平衡参数;k1(xi,xj)为多项式核函数,数学表达式为:

k1(xi,xj)=(1+xi·xj)d

(14)

式中:d为多项式系数。

k2(xi,xj)为高斯径向基核函数,数学表达式为:

(15)

式中:σ为核宽度。

3.2 BA-MKELM模型及故障识别与定位流程

MKELM的关键参数为正则化系数C、平衡参数λ、多项式系数d和核宽度σ,这些重要参数的取值对MKELM的诊断精度影响非常大。本文利用BA对这些参数进行寻优,BA全局寻优能力强,可通过较少的迭代计算快速准确地找出全局最优值。概率模型采用高斯过程模型,采集函数选用期望改进(IE)确定下一评估点,在寻优过程中,将不同参数组合作为自变量x′=[C,λ,d,σ],以五折交叉验证评估得到的均方误差(MSE)作为贝叶斯网络的输出t。五折交叉验证是将小波包分解提取到的故障数据样本分为5份,依次将其中4份做训练,另一份做测试,贝叶斯网络的输出取5次测试结果的误差均值。基于BA-MKELM的微电网故障识别与定位的详细流程图如图2所示。

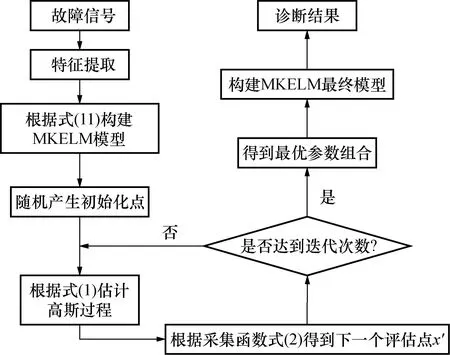
图2 BA优化MKELM的流程图Fig.2 Flow chart of BA optimizing MKELM

4 实验验证

4.1 数据采集

考虑包含风力发电、光伏发电和蓄电池储能的微电网并网运行系统,结构图如图3所示。

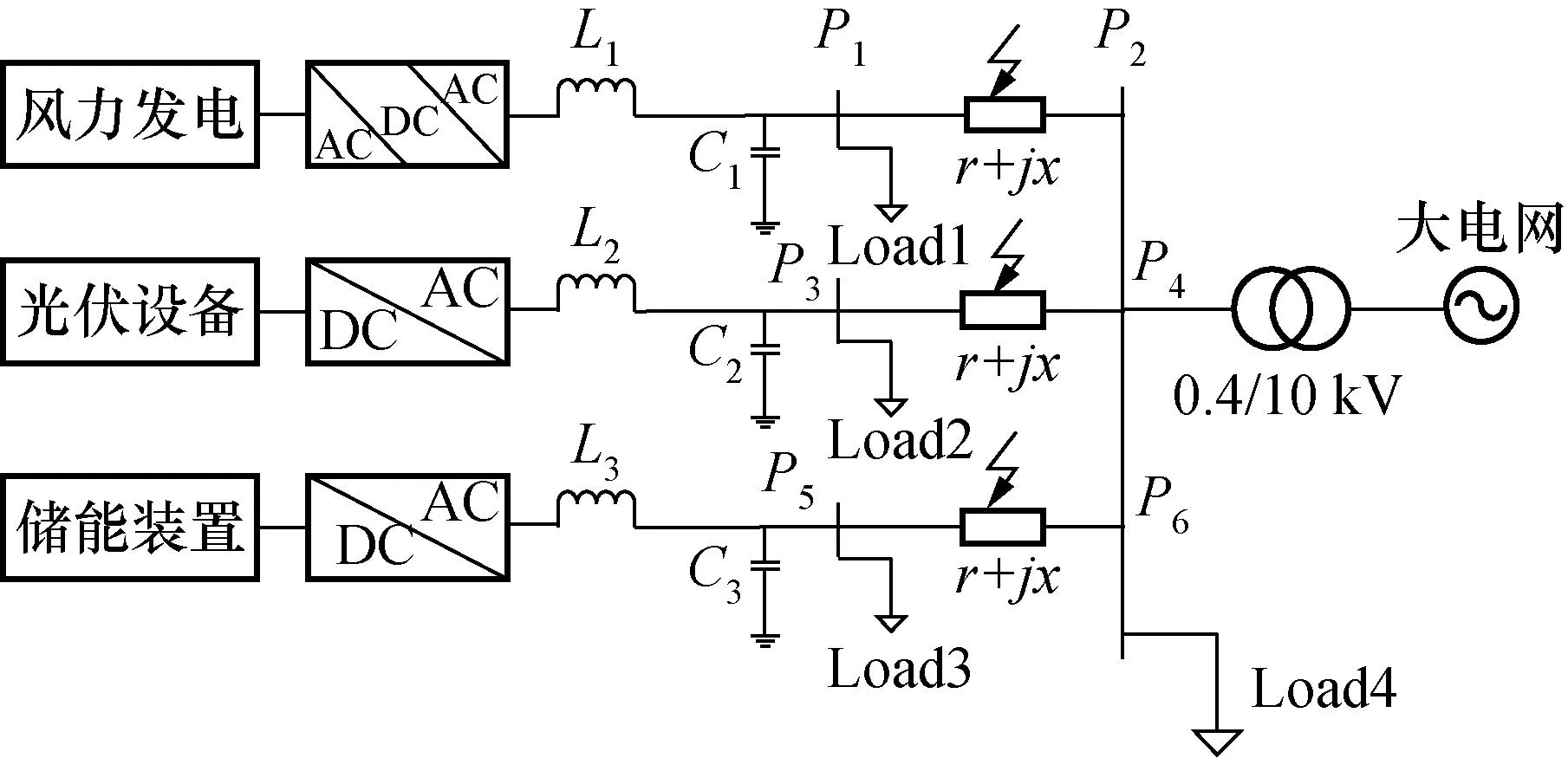
图3 微电网系统结构图Fig.3 Structure diagram of microgrid system

在图3中,风力发电系统采用双馈变速风力发电机组(18 kW),经过整流得到直流再逆变成交流,得到稳定的交流电后与大电网相连;光伏发电系统(30 kW)经过DC/AC电源模块得到交流电后并入大电网;燃料电池发电系统(10 kW)利用DC/AC变换器将燃料电池堆的输出转换成交流电实现并网;采用蓄电池储能系统作为储能装置。L1、L2、L3为滤波电感,其值都为3e-3H:C1,C2、C3为滤波电容,其值都为250e-6F,Load1(10 kVA)、Load2(8 kVA)、Load3(5 kVA)、Load4(15 kVA)为用电负荷,r=0.125 Ω/km和x=0.072 Ω/km分别为线路电阻和电抗。每条输电线路总长度为2 km。

为了评估本文所提故障识别和定位方法的性能,根据图3所示的微电网系统结构图,在MATLAB/Simulink平台构建了微电网仿真模型。分别对每段配电线路(P1-P2、P3-P4、P5-P6)故障进行仿真,每条线路每隔10%取一个故障点,采集各个故障点的所有故障类型的三相故障电压。选取db6小波作为小波基函数,分解由仿真得到的三相故障电压信号,分解的层数为3层。分别对每相电压的故障特征进行提取,计算其小波包系数的方差、标准差、最大值、最小值、平均值、峰-峰值、整流平均值、方根、均方根、峭度、偏度、波形因子、峰值因子、脉冲因子和裕度因子共15个特征值,A、B、C三相共得到45个特征值,将其组成特征向量作为网络的输入X={x1,x2,…,x45}T。网络的输出为Y={y1,y2,y3,y4,y5}T,y1、y2和y3分别表示当系统出现故障时,A相、B相和C相的工作状态,y4表示当前故障类型是否为接地故障类型。当其为0时,代表该相处于正常工作状态或当前所发生的故障不是接地故障类型;当其为1时,则代表该相发生故障或此时发生的故障为接地故障类型。y5表示故障点在线路中的具体位置,取值为0.2～1.8,因每条输电线路总长度为2 km,如当y5=0.2时,表示此时故障点在线路位置10%处。

4.2 故障识别结果及分析

微电网故障类型的识别是故障分析和定位的前提,本文考虑了所有类型的线路故障,包括单线对地故障(ag、bg和cg)、线对线故障(ab、bc和ac)、双线对地故障(abg、bcg和acg)、三线故障(abc)和三线对地故障(abcg)。将每条线路位置10%、20%、30%、40%、50%、60%、70%、80%、90%处的故障样本作为训练样本,35%、55%、75%处的故障样本作为测试样本,对BA-MKELM模型的故障识别性能进行评估。

将所有数据样本带入BA-MKELM故障诊断模型中进行训练和测试,得到P1与P2之间线路位置55%处测试样本线路故障识别结果如图4所示(限于篇幅35%和75%处测试样本线路故障识别结果省略)。为了验证BA-MKELM诊断模型的优越性,同时给出ELM和MKELM诊断模型的结果进行对比。

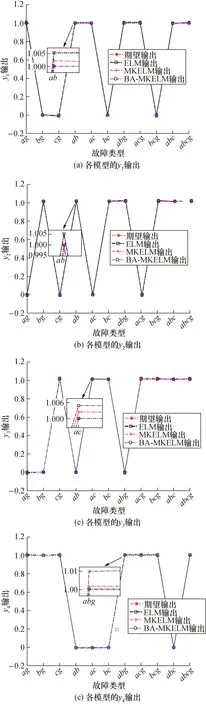
图4 55%处测试样本结果图Fig.4 Figure of test sample results at 55%

从图4中可以明显看出BA-MKELM模型的逼近能力最强。为了更全面、精确地比较这3种模型的优劣,根据式(16)计算这3种模型所有测试样本实际输出结果与目标期望输出结果的均方误差EMS进行对比分析。

(16)

式中:Qi为第i个样本的实际输出值;Yi为第i个样本的目标期望输出值。

BA-MKELM模型、MKELM模型和ELM模型所有测试样本的均方误差如表1所示。

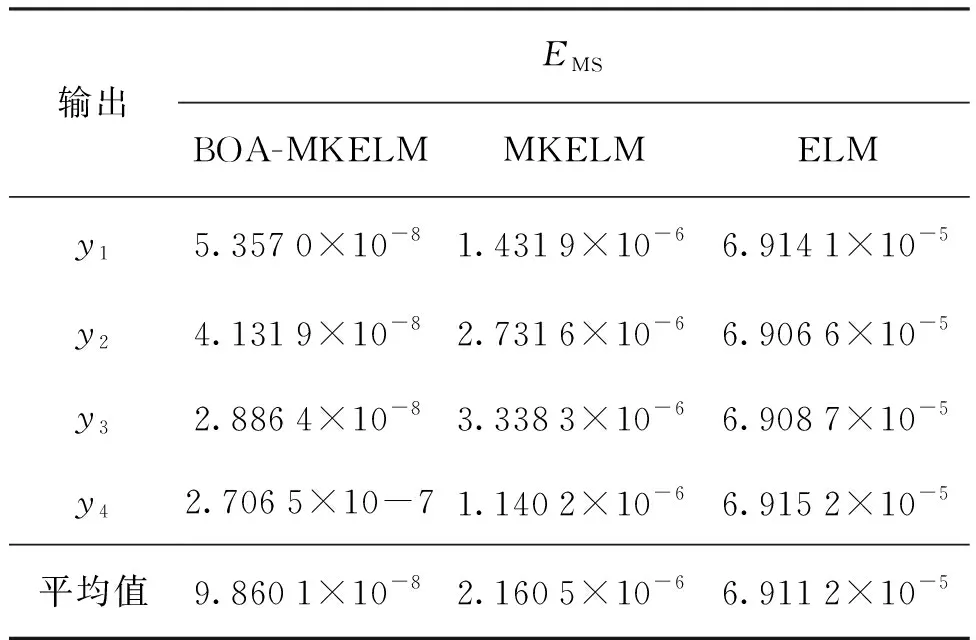
表1 各模型所有测试样本的均方误差Tab.1 The mean square error of all test samples of each model

从表1可以看出,BA-MKELM模型4个输出的均方误差均比MKELM模型4个输出的均方误差小约两个数量级,比ELM模型4个输出的均方误差小近3个数量级,识别效果最好,结果最准确,精度最高,可以有效地对故障类型进行准确识别。

4.3 故障定位结果及分析

在对故障类型进行分类识别的同时,也根据不同故障特征对模型的故障定位性能进行了评估。图5给出了在不同故障类型的情况下,峭度、标准差、脉冲因子和裕度因子等4种故障特征在不同故障位置的变化情况。

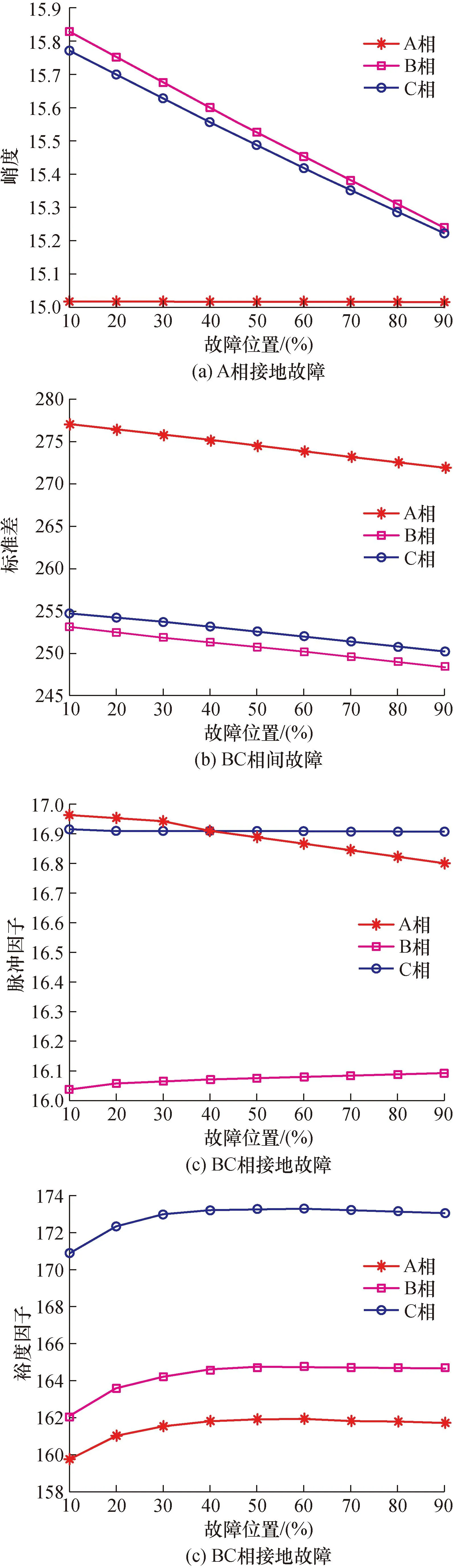
图5 故障特征随故障位置的变化Fig.5 Change of fault characteristics with fault location

由图5可以看出,同一故障类型在不同故障位置处的这些故障特征之间差异较大,因此通过这些故障特征可实现对故障的准确定位。

线路P1与P2之间测试样本的具体故障定位结果如图6所示。

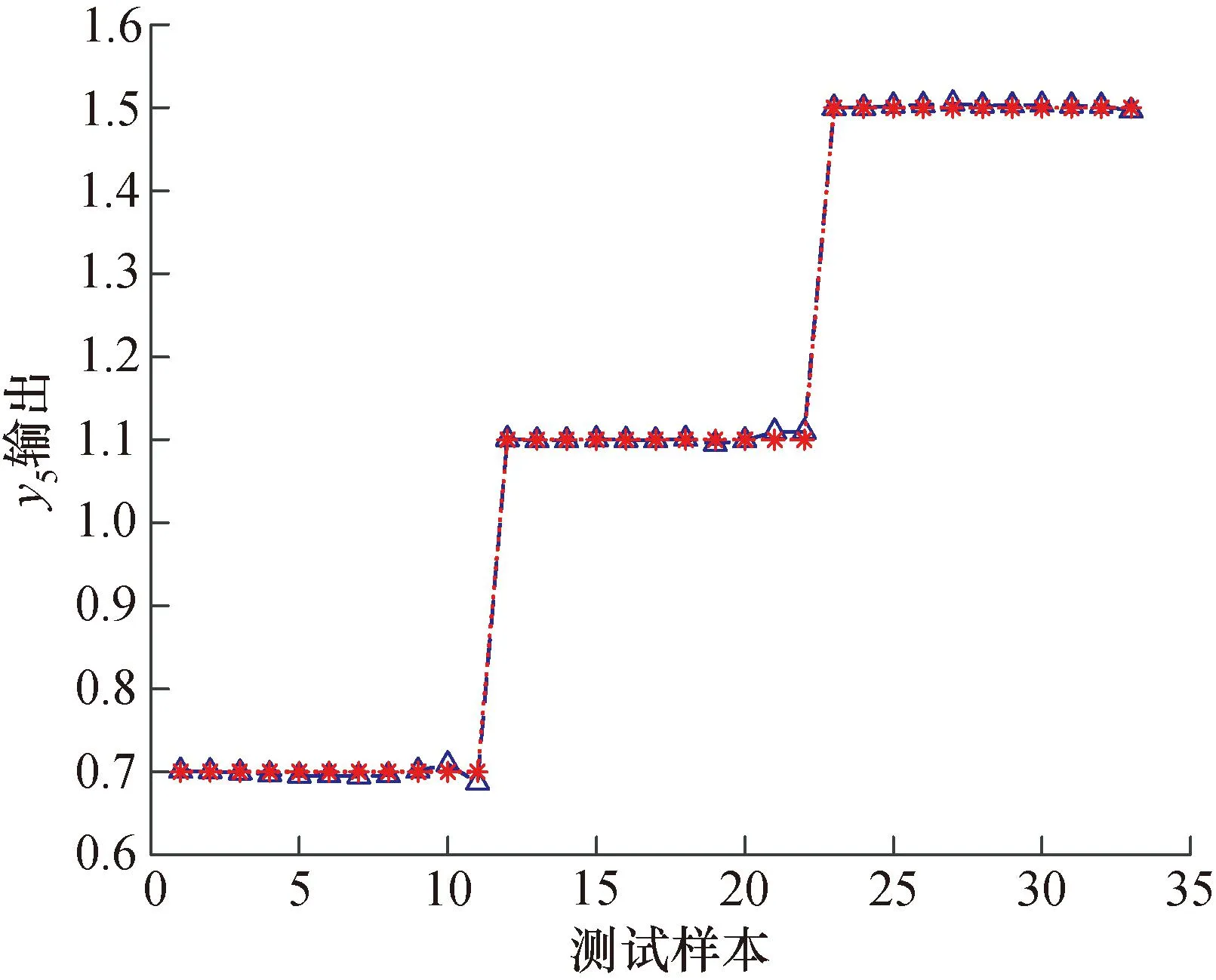
图6 测试样本的故障定位结果图Fig.6 Diagram of fault location results of test samples

图6中,样本1～11、12～22、23～33分别为线路P1与P2之间所有故障类型在35%、55%、75%处的定位结果,可看出实际定位结果与期望定位结果之间误差较小,可对故障位置进行准确定位。

为了进一步验证BA-MKELM模型的故障定位性能,利用式(17)计算每种故障类型的定位误差率。图7给出了所有故障类型的故障定位结果的误差率。

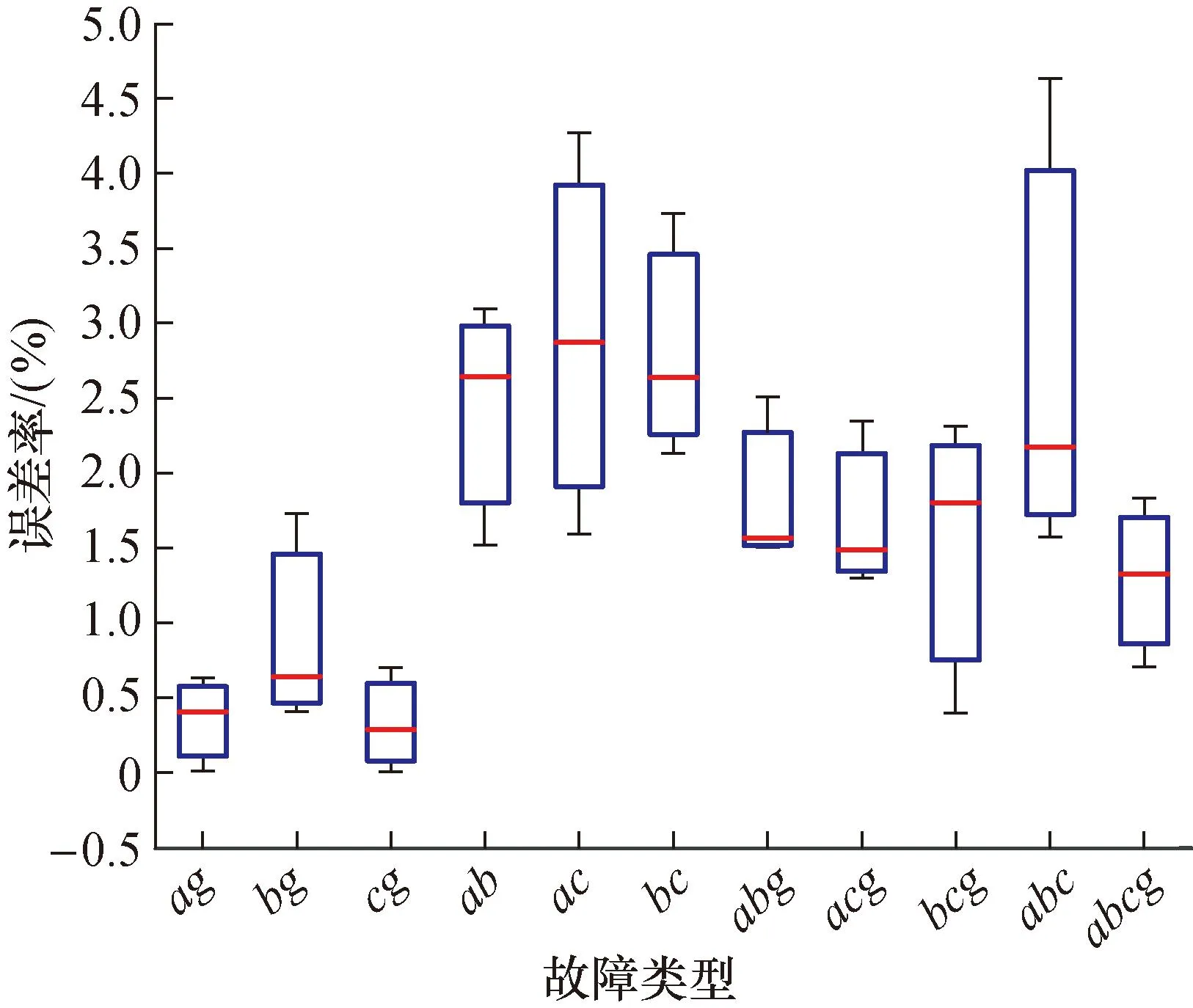
图7 故障定位结果的误差率Fig.7 Error rate of fault location results

(17)

式中:y5为实际输出故障位置;t5为期望输出故障位置;l为输电线路总长度。

由图7可看出,故障定位结果的总体误差在0.34%～2.92%之间,总体平均误差为1.76%。

为了进一步验证BA-MKELM模型故障定位的优越性,将BA-MKELM模型与基于MKELM和ELM的故障定位方法进行对比分析,3种方法的故障定位结果的总体平均误差率如表2所示。

表2 3种方法的故障定位结果误差率Tab.2 Error rate of fault location results of three methods (%)

表2的测试结果表明,与其它两种方法相比,本文所提方法具有较小的故障定位百分比误差,可以很好地实现对故障位置的准确定位。

4.4 改变微电源数量时的故障诊断及定位结果分析

实际微电网中,风电、储能、光伏设备均可能包含多个,其数量的增加或减少是否对所提方法有影响,需进一步验证。考虑微电网中风电增加的情况,由原来的18 kW增加到36 kW,得到的各模型的故障诊断和定位结果如表3和表4所示。

表3 各模型所有测试样本的均方误差Tab.3 The mean square error of all test samples of each model

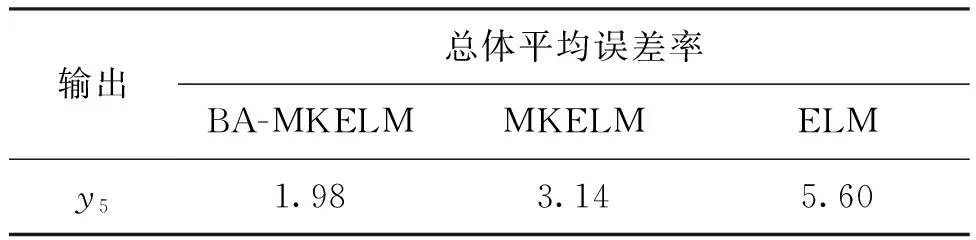
表4 3种方法的故障定位结果误差率Tab.4 Error rate of fault location results of three methods (%)

从表3可以看出,随着风电增加,3个模型故障诊断结果的均方误差变化不大,特别是数量级未变,原因是微电源(风电,储能和光伏)的增加是并入(并联)系统的,所以电压不变,因此线路故障时的电压变化情况相同;功率增加只改变电流(增加),而故障电流都是极端情况,与正常工作电流相比都会有明显变化,且每个故障电流之间也有明显不同。功率增加时正常工作电流会增大,因此故障电流也会同比例增大,由于采用归一化参数训练网络,则这种成比例的变化对故障诊断的结果影响不大。由表4可看出,由于采用归一化参数训练网络,随着风电增加,对定位结果影响也不大。

5 结 论

提出了一种基于BA-MKELM诊断模型的微电网故障识别和定位新方法。针对ELM输入参数和隐含层节点数随机选取导致回归能力不足的问题,在ELM的隐层节点中,引入核函数,并将多项式与高斯径向基核函数相结合构成MKELM故障诊断模型。为了进一步提高模型的逼近能力,利用BA全局寻优能力强,可通过较少的迭代计算快速准确地找出全局最优值的特点,对MKELM相关参数进行优化,得到BA-MKELM故障诊断模型。对微电网中不同的故障案例进行了性能测试,并与MKELM和ELM诊断模型进行对比分析。结果表明,BA-MKELM诊断模型能够高效、准确地识别和定位微电网中任意类型的故障。

不足之处,BA-MKELM诊断模型的精度仍高度依赖于数据的大小和准确性,需要大量的数据作保证。如何从数据中提取特征,归纳、推理,在不影响精度的前提下减少数据量是进一步要考虑的问题。